代码签名证书续费
代码签名证书的有效周期是1-3年,这种情况下证书到期了就要重新申请办理,最开始同样的申请验证步骤还要再走一遍,尤其是Ukey还是要CA机构重新颁发,还是要等待快递配送。
OV代码签名证书、EV代码签名证书目前行业内统一采取Ukey存储,快递配送到申请单位。
 代码签名证书快速续费
代码签名证书快速续费
无论你之前选择的是DigiCert、Sectigo还是Globalsign的代码签名证书,也无论是OV还是EV,都可以直接在JoySSL官网申请快速续费,提交订单,CA审核,快递签发。点击了解代码签名证书:
代码签名证书续签
关于代码签名证书,一般建议单位一次申请多年,避免每年年审带来的麻烦,影响项目进程。
相关文章:

代码签名证书续费
代码签名证书的有效周期是1-3年,这种情况下证书到期了就要重新申请办理,最开始同样的申请验证步骤还要再走一遍,尤其是Ukey还是要CA机构重新颁发,还是要等待快递配送。OV代码签名证书、EV代码签名证书目前行业内统一采取Ukey存储&…...
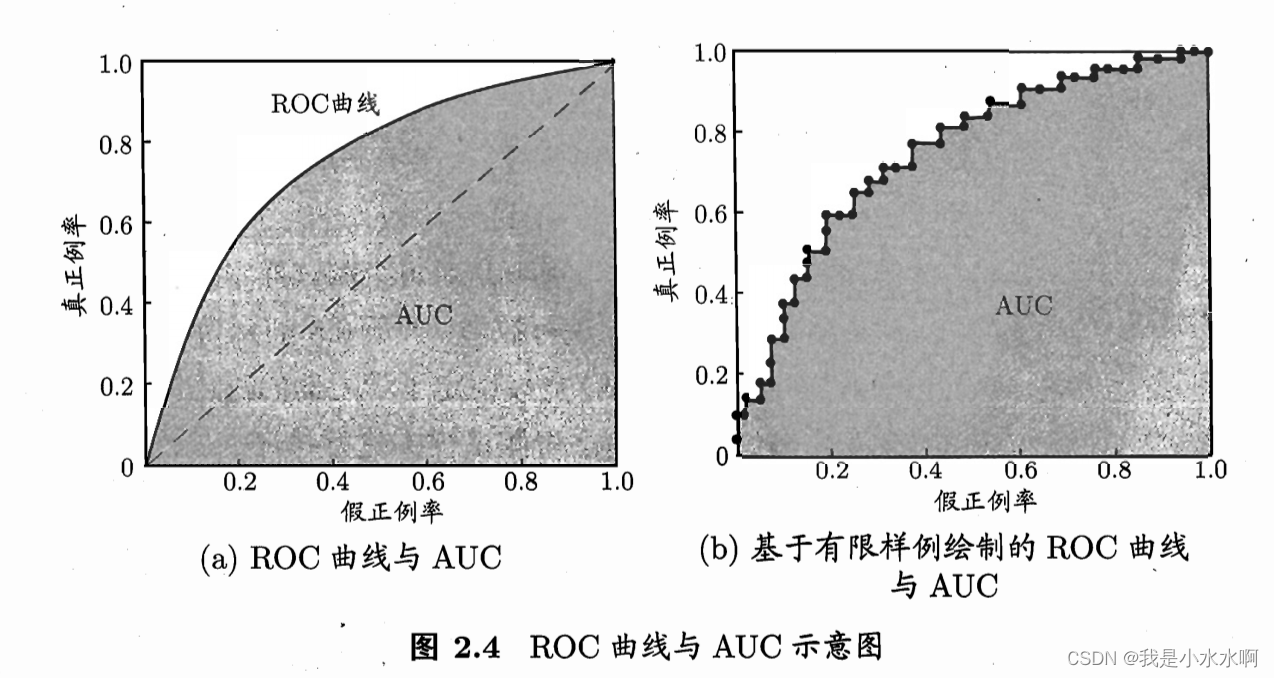
机器学习之ROC与AUC
文章目录 定义ROC曲线:AUC(Area Under the ROC Curve): 定义 ROC(Receiver Operating Characteristic)曲线和AUC(Area Under the ROC Curve)是用于评估二分类模型性能的重要工具。 …...
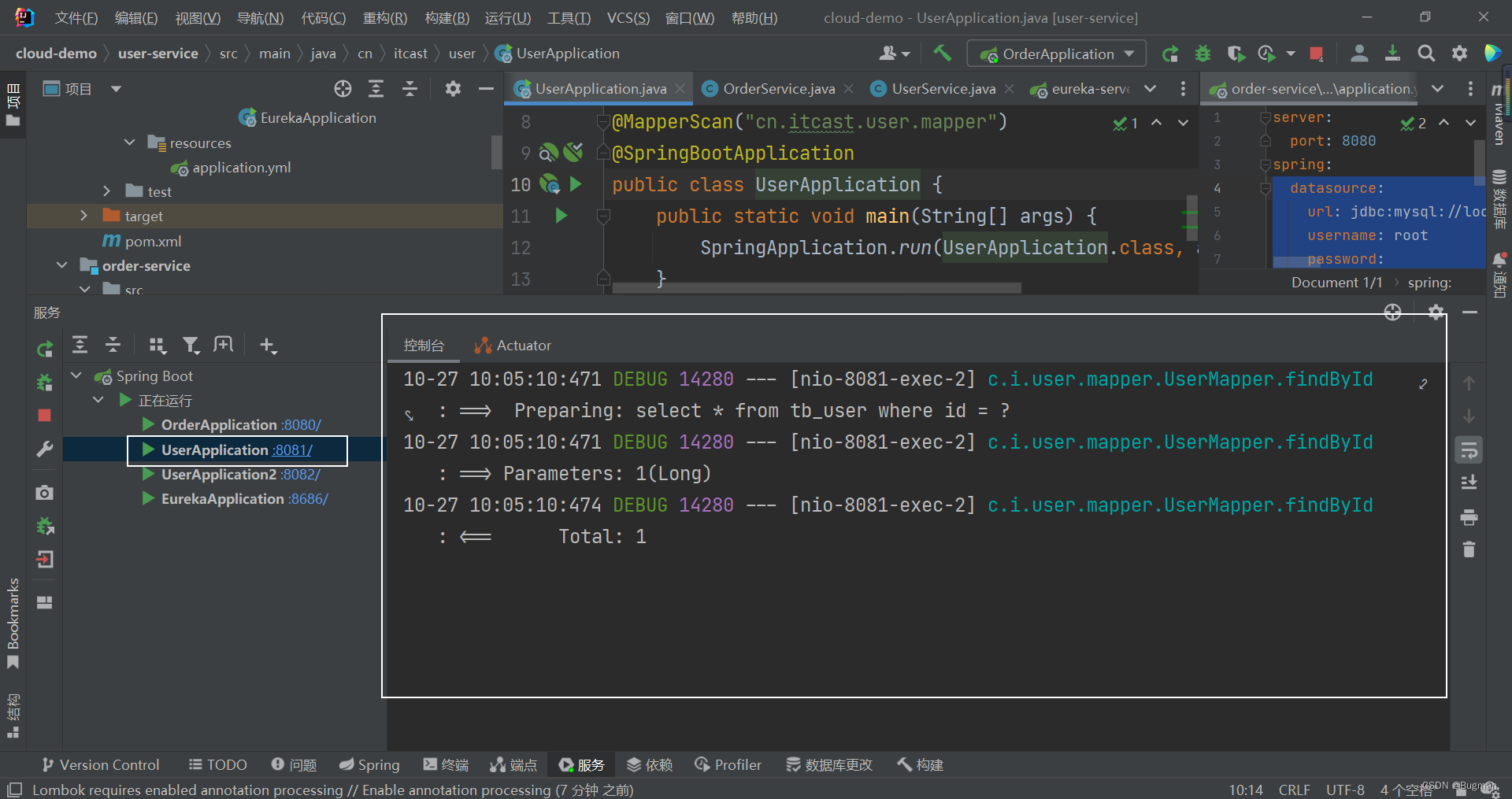
实用篇-Eureka注册中心
一、提供者与消费者 服务提供者:一次业务中,被其他微服务调用的服务。(提供接口给其他微服务) 服务消费者:一次业务中,调用其他微服务的服务。(调用其他微服务提供的接口) 例如前面的案例中,order-service微服务是服…...
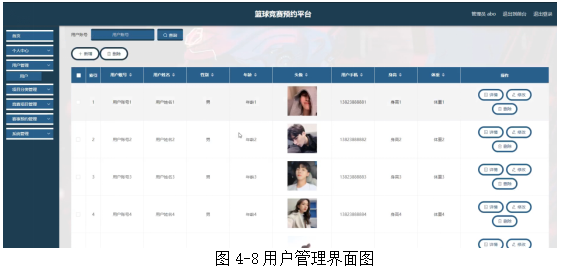
基于springboot实现篮球竞赛预约平台管理系统项目【项目源码+论文说明】
基于springboot实现篮球竞赛预约平台管理系统演示 摘要 随着信息化时代的到来,管理系统都趋向于智能化、系统化,篮球竞赛预约平台也不例外,但目前国内仍都使用人工管理,市场规模越来越大,同时信息量也越来越庞大&…...
OpenHarmony docker环境搭建所见的问题和解决
【摘要】OpenHarmony docker环境搭建需要一台安装Ubuntu的虚拟机,并且虚拟机中需要有VScode。 整个搭建流程请参考这篇博客:OpenHarmony docker环境搭建-云社区-华为云 (huaweicloud.com) 上篇博主是用Ubuntu的服务器进行环境搭建的,在使用VS…...
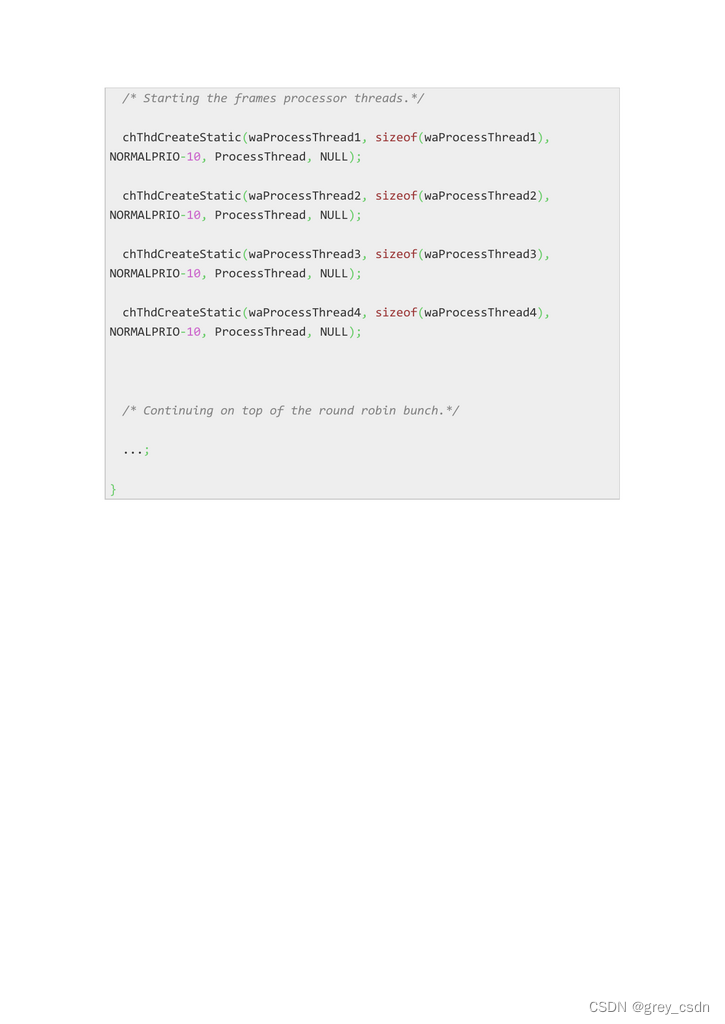
1817_ChibiOS的RT线程
全部学习汇总: GreyZhang/g_ChibiOS: I found a new RTOS called ChibiOS and it seems interesting! (github.com) 1. 关于线程,有几个概念需要弄清楚:声明、生命循环、延迟、线程引用、线程队列、线程时间、优先级管理、调度。 2. 两个声明…...

牛客网刷题-(7)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...

多模态领域的先进模型
多模态学习领域涌现了许多先进的模型,这些模型能够处理来自不同感官模态的信息并实现多模态任务。以下是一些先进的多模态学习模型: CLIP (Contrastive Language-Image Pretraining):由OpenAI开发的CLIP是一种多模态预训练模型,能…...

列表自动向上滚动
列表自动向上滚动 鼠标放上去 自动停止滚动 <div id"list-detail-main"><div class"my_table_thead_tr"><div v-for"(item, index) in header" :key"index" class"my_table_thead_th">{{ item }}</div…...

嘴笨的技术人员怎么发言
对于嘴笨的人来说,即兴发言简直就是灾难,想想自己窘迫的模样,自己都受不了,但职场又避免不了这种场合,所以,就要靠一些技巧让我们顺利打开思路了。 那么,今天就分享几个解救过我的不同场景即兴发…...
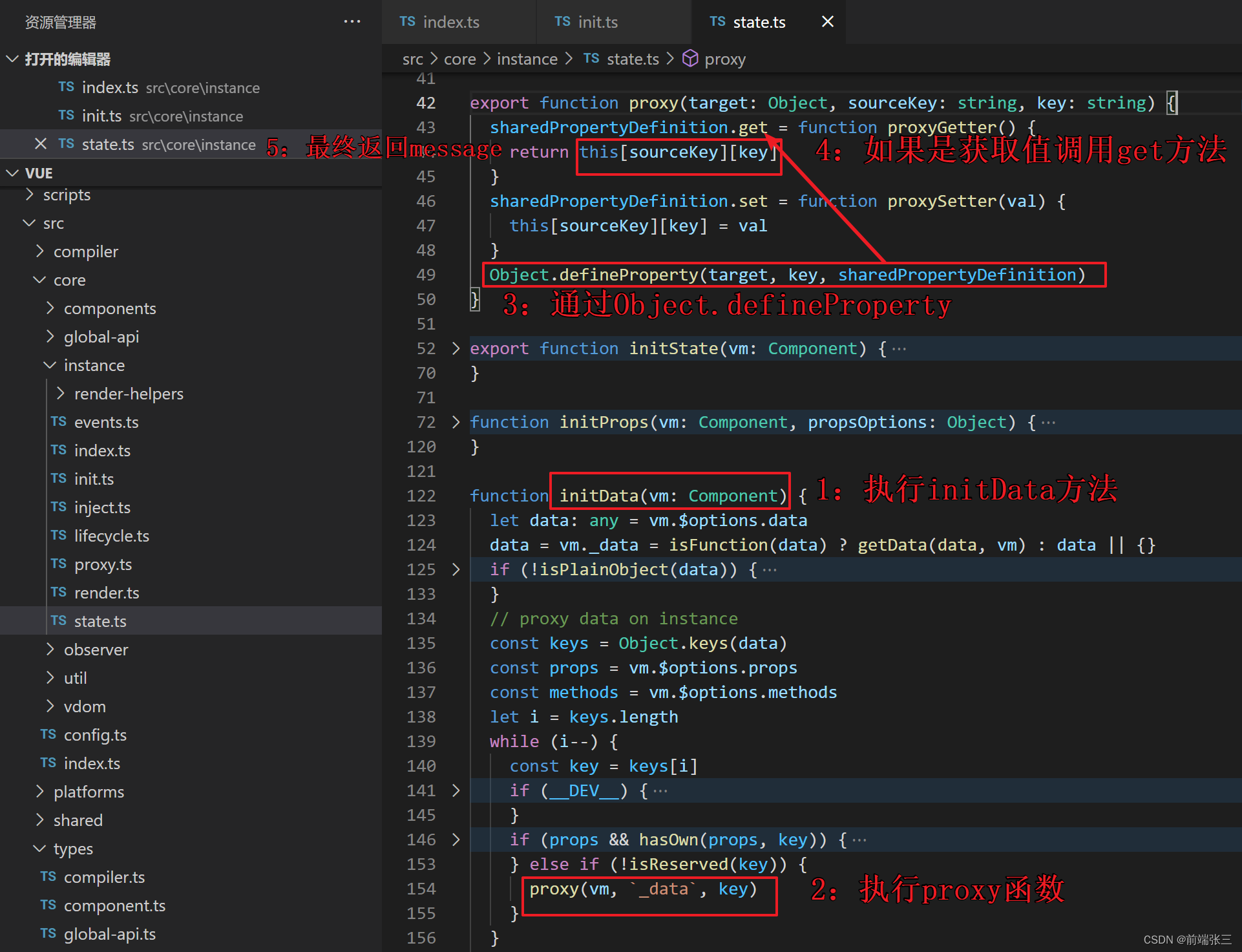
vue源码分析(三)——new Vue 的过程(详解data定义值后如何获取的过程)
文章目录 零、准备工作1.创建vue2项目2.修改main.js 一、import Vue from vue引入的vue是哪里来的(看导入node_modules包)1: 通过node_modules包的package.json文件2: 通过配置中的main入口文件进入开发环境的源码(1&a…...
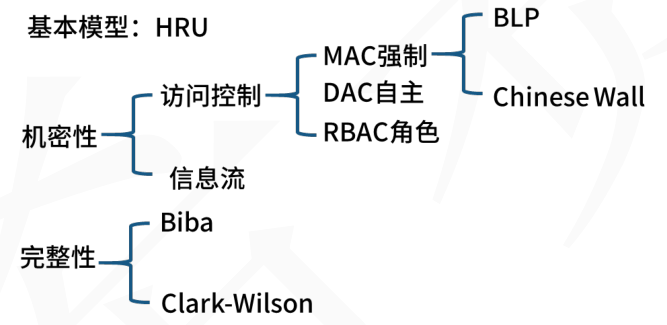
软考系统架构师知识点集锦四:信息安全技术基础知识
一、考情分析 二、考点精讲 2.1信息加解密技术 2.1.1对称加密 概念:对称加密(又称为私人密钥加密/共享密钥加密) : 加密与解密使用同一密钥。特点:加密强度不高,但效率高;密钥分发困难。 (大量明文为了保证加密效率一般使用对称加密) 常见对称密钥加密算法:DES:…...

Vscode中不显示.ipynb文件单元格行号
找到设置,搜索line number: 看到下面那个Notebook: Line Numbers 控制单元格编辑器中行号的显示。,选择on即可;...
【Oracle】[INS-30131]执行安装程序验证所需的初始设置失败。
这里写目录标题 一、问题描述1 报错内容1.1 无法从节点“kotin”检索 exectask 的版本1.2 工作目录"xxx"无法在节点"kotin"上使用 2 相关环境2.1 安装软件2.2 安装系统 3 解决思路分析 二、解决方案1 方案一、 满足验证条件 - 不换系统1.1 第一步、检查文件…...

二进制部署kubernetes集群的推荐方式
软件版本: 软件版本containerdv1.6.5etcdv3.5.0kubernetesv1.24.0 一、系统环境 1.1 环境准备 角色IP服务k8s-master01192.168.10.10etcd、containerd、kube-apiserver、kube-scheduler、kube-controller-manager、kubele、kube-proxyk8s-node01后续etcd、conta…...

智能矩阵,引领商业新纪元!拓世方案:打破线上线下界限,开启无限营销可能!
在科技赋能商业大潮中,一切行业都在经历巨大变革,传统的营销策略被彻底改变,催生着无数企业去打造横跨线上线下、多维度、全方位的矩阵营销帝国。无数的成功案例已经告诉我们,营销不再只是宣传,而是建立品牌与消费者之…...
)
ADB原理(第四篇:聊聊adb shell ps与adb shell ps有无双引号的区别)
前言 对于经常使用adb的同学,不可避免的一定会这样用adb,比如我们想在手机里执行ps命令,于是在命令行中写下如下代码: adb shell ps -ef 或者 adb shell "ps -ef" 两种方式都可以使用,你喜欢用哪个呢&#…...
「网络编程」数据链路层协议_ 以太网协议学习
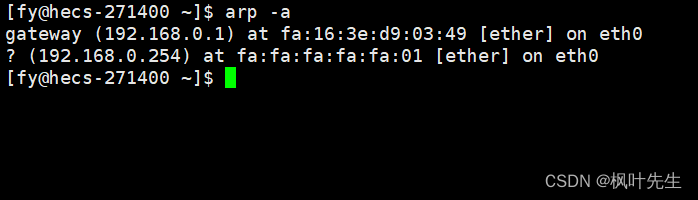
「前言」文章内容是数据链路层以太网协议的讲解。 「归属专栏」网络编程 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、以太网协议简介二、以太网帧格式(报头)三、MTU对上层协议的影响四、ARP协议4.1 ARP协议的作用4.2 ARP协议报头 一、以太网协…...
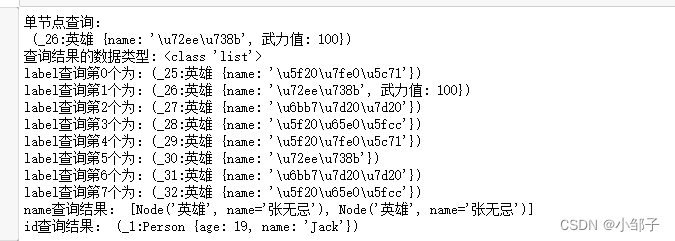
通过python操作neo4j
在neo4j中创建结点和关系 创建结点 创建电影结点 例如:创建一个Movie结点,这个结点上带有三个属性{title:‘The Matrix’, released:1999, tagline:‘Welcome to the Real World’} CREATE (TheMatrix:Movie {title:The Matrix, released:1999, tagl…...
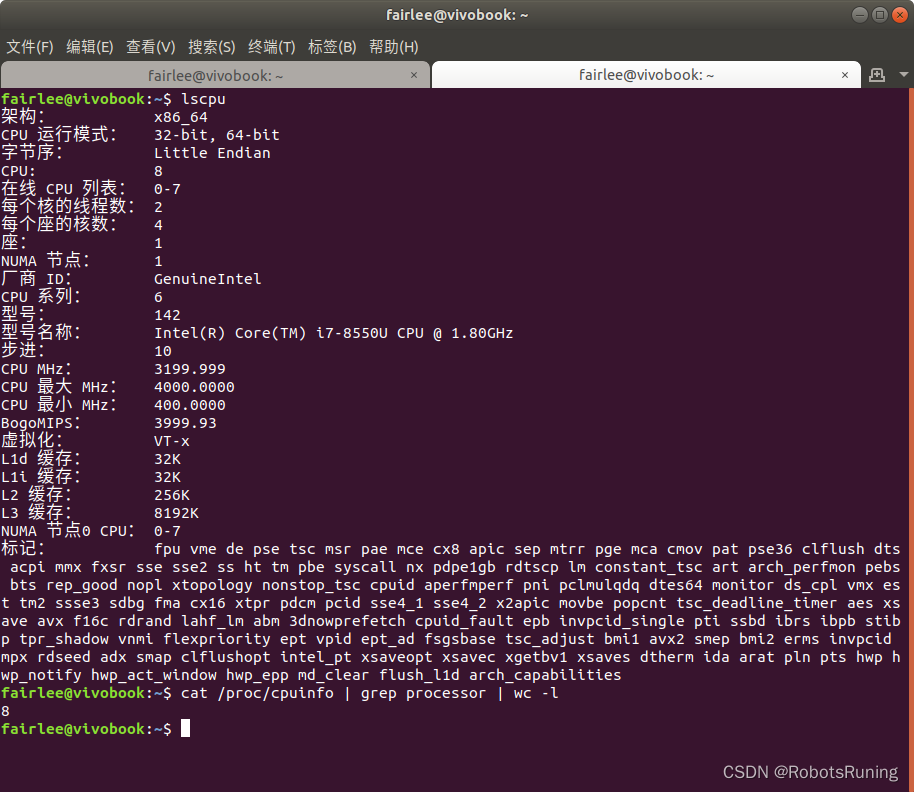
Ubuntu中查看电脑有多少个核——lscpu
1. 使用lscpu命令: 打开终端并输入以下命令: lscpu你会看到与CPU相关的详细信息。查找"CPU(s)"这一行来看总的核心数。另外,“Core(s) per socket”表示每个插槽或每个物理CPU的核数,“Socket(s)”表示物理CPU的数量。将这两个值相乘即得到总…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
