Python3-数字
Python3 数字(Number)
Python 数字数据类型用于存储数值。
数据类型是不允许改变的,这就意味着如果改变数字数据类型的值,将重新分配内存空间。
Python 支持三种不同的数值类型:
整型(int) - 通常被称为是整型或整数,是正或负整数,不带小数点。Python3 整型是没有限制大小的,可以当作 Long 类型使用,所以 Python3 没有 Python2 的 Long 类型。布尔(bool)是整型的子类型。
浮点型(float) - 浮点型由整数部分与小数部分组成,浮点型也可以使用科学计数法表示(2.5e2 = 2.5 x 102 = 250)
复数( (complex)) - 复数由实数部分和虚数部分构成,可以用a + bj,或者complex(a,b)表示, 复数的实部a和虚部b都是浮点型。
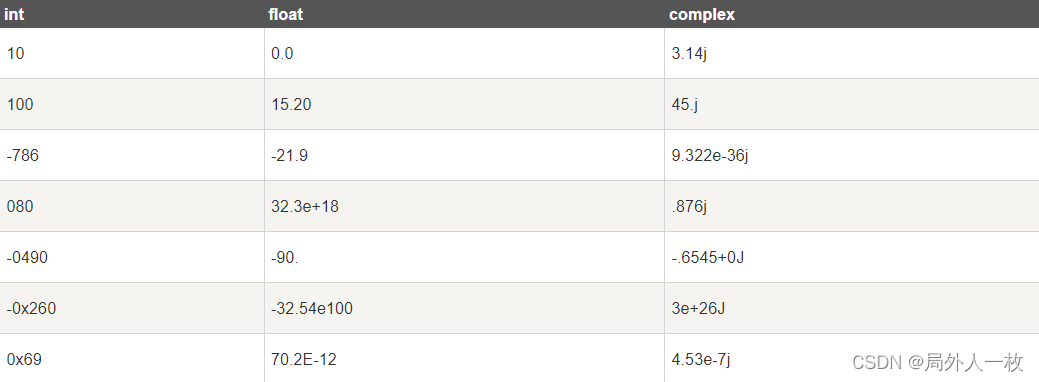
Python支持复数,复数由实数部分和虚数部分构成,可以用a + bj,或者complex(a,b)表示, 复数的实部a和虚部b都是浮点型。
Python 数字类型转换
有时候,我们需要对数据内置的类型进行转换,数据类型的转换,你只需要将数据类型作为函数名即可。
int(x) 将x转换为一个整数。
float(x) 将x转换到一个浮点数。
complex(x) 将x转换到一个复数,实数部分为 x,虚数部分为 0。
complex(x, y) 将 x 和 y 转换到一个复数,实数部分为 x,虚数部分为 y。x 和 y 是数字表达式。
以下实例将浮点数变量 a 转换为整数:
>>> a = 1.0
>>> int(a)
1
Python 数字运算
Python 解释器可以作为一个简单的计算器,您可以在解释器里输入一个表达式,它将输出表达式的值。
表达式的语法很直白: +, -, * 和 /, 和其它语言(如Pascal或C)里一样。例如:
>>> 2 + 2
4
>>> 50 - 5*6
20
>>> (50 - 5*6) / 4
5.0
>>> 8 / 5 # 总是返回一个浮点数
1.6
注意:在不同的机器上浮点运算的结果可能会不一样。
在整数除法中,除法 / 总是返回一个浮点数,如果只想得到整数的结果,丢弃可能的分数部分,可以使用运算符 // :
>>> 17 / 3 # 整数除法返回浮点型
5.666666666666667
>>>
>>> 17 // 3 # 整数除法返回向下取整后的结果
5
>>> 17 % 3 # %操作符返回除法的余数
2
>>> 5 * 3 + 2
17
注意:// 得到的并不一定是整数类型的数,它与分母分子的数据类型有关系。
>>> 7//2
3
>>> 7.0//2
3.0
>>> 7//2.0
3.0
>>>
等号 = 用于给变量赋值。赋值之后,除了下一个提示符,解释器不会显示任何结果。
>>> width = 20
>>> height = 5*9
>>> width * height
900
Python 可以使用 ** 操作来进行幂运算:
>>> 5 ** 2 # 5 的平方
25
>>> 2 ** 7 # 2的7次方
128
变量在使用前必须先"定义"(即赋予变量一个值),否则会出现错误:
>>> n # 尝试访问一个未定义的变量
Traceback (most recent call last):File "<stdin>", line 1, in <module>
NameError: name 'n' is not defined
不同类型的数混合运算时会将整数转换为浮点数:
>>> 3 * 3.75 / 1.5
7.5
>>> 7.0 / 2
3.5
在交互模式中,最后被输出的表达式结果被赋值给变量 _ 。例如:
>>> tax = 12.5 / 100
>>> price = 100.50
>>> price * tax
12.5625
>>> price + _
113.0625
>>> round(_, 2)
113.06
数学函数
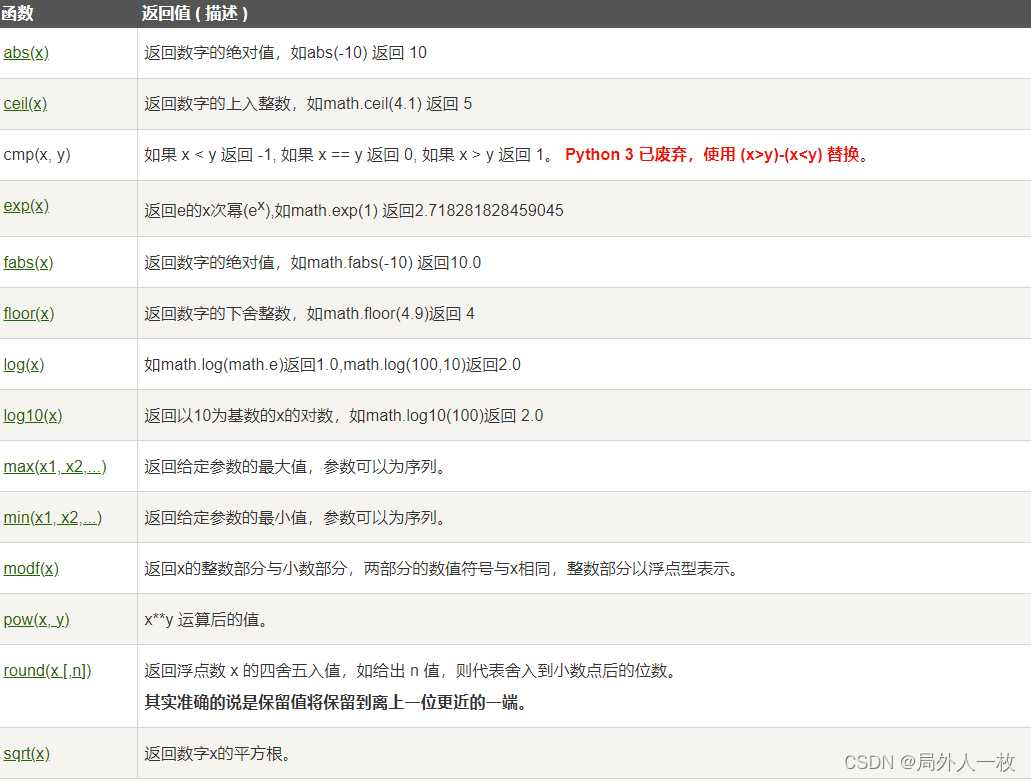
随机数函数
随机数可以用于数学,游戏,安全等领域中,还经常被嵌入到算法中,用以提高算法效率,并提高程序的安全性。
Python包含以下常用随机数函数:

三角函数
Python包括以下三角函数:
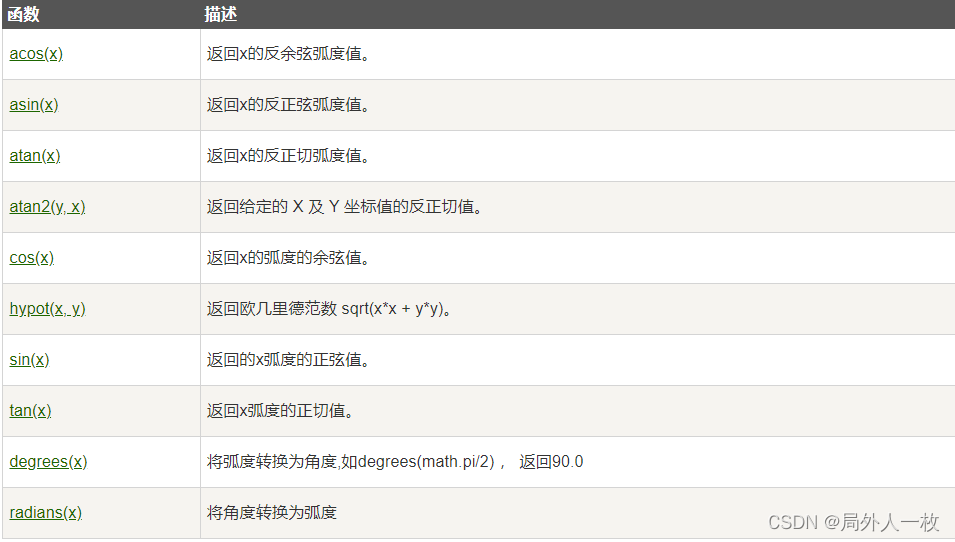
数学常量

相关文章:

Python3-数字
Python3 数字(Number) Python 数字数据类型用于存储数值。 数据类型是不允许改变的,这就意味着如果改变数字数据类型的值,将重新分配内存空间。 Python 支持三种不同的数值类型: 整型(int) - 通常被称为是整型或整数,是正或负整数&#x…...
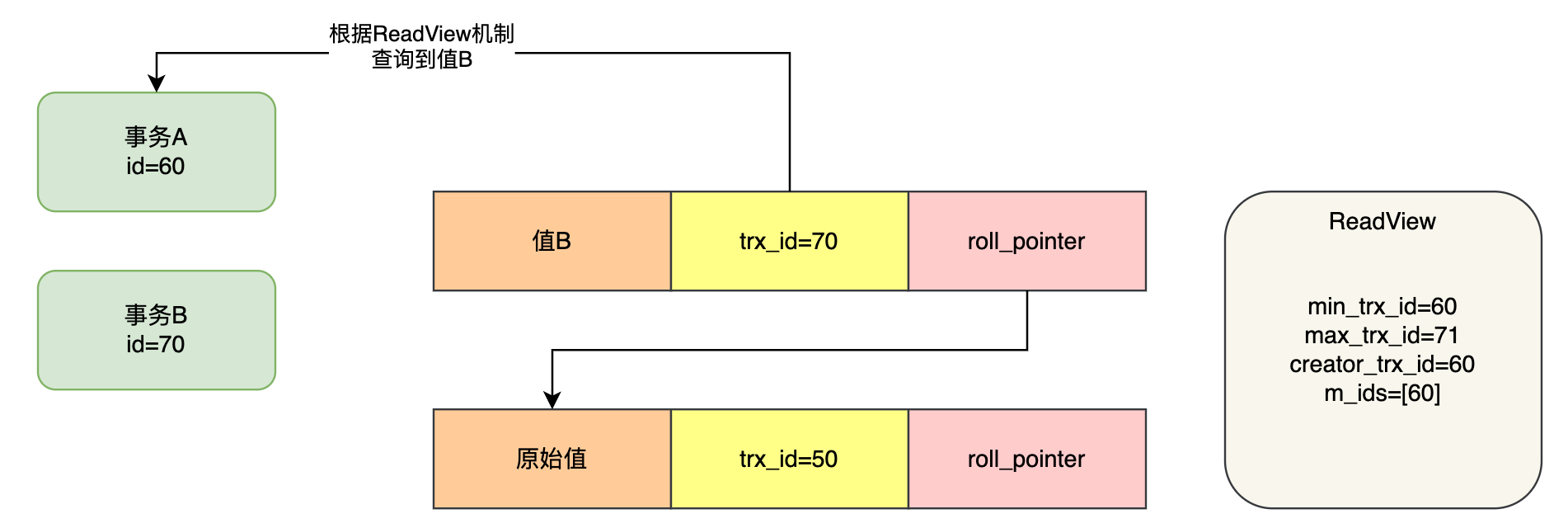
(四十一)Read Committed隔离级别是如何基于ReadView机制实现的?
今天我们来给大家讲一下,基于之前我们说的ReadView机制是如何实现Read Committed隔离级别的,那么当然了,首先就是要先做一些简单的回顾。所谓的Read Committed隔离级别,我们可以用骚气一点的名字,就是简称为 RC 隔离级…...

React echarts封装
做大屏的时候经常会遇到 echarts 展示,下面展示在 React (^18.2.0) 中对 echarts (^5.4.0) 的简单封装。 文章首发于https://blog.fxss.work/react/echarts封装.html,样例查看 echarts 封装使用 props 说…...

【C语言进阶】了解计算机的程序环境和预处理过程 掌握计算机预处理操作
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C语言进阶 🎯长路漫漫浩浩,万事皆有期待 文章目录1.编译与链接1.1 程…...
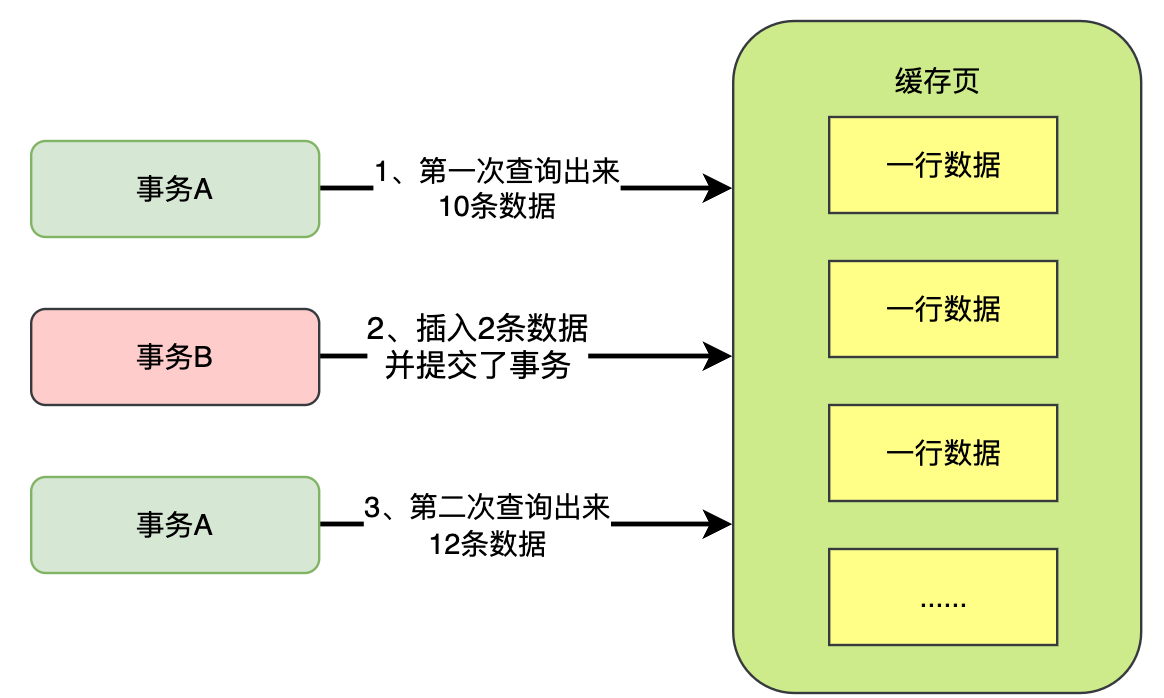
(三十六)大白话数据库幻读,本质到底是个什么问题?
上一讲我们给大家讲解了不可重复读这个问题,这个问题简单来说,就是一个事务多次查询一条数据,结果每次读到的值都不一样,这个过程中可能别的事务会修改这条数据的值,而且修改值之后事务都提交了,结果导致人…...
【算法经典题集】递归(持续更新~~~)
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法经典题集🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用💪种一棵树最好是十年前其次是现在1.递归1.1 递归实现…...
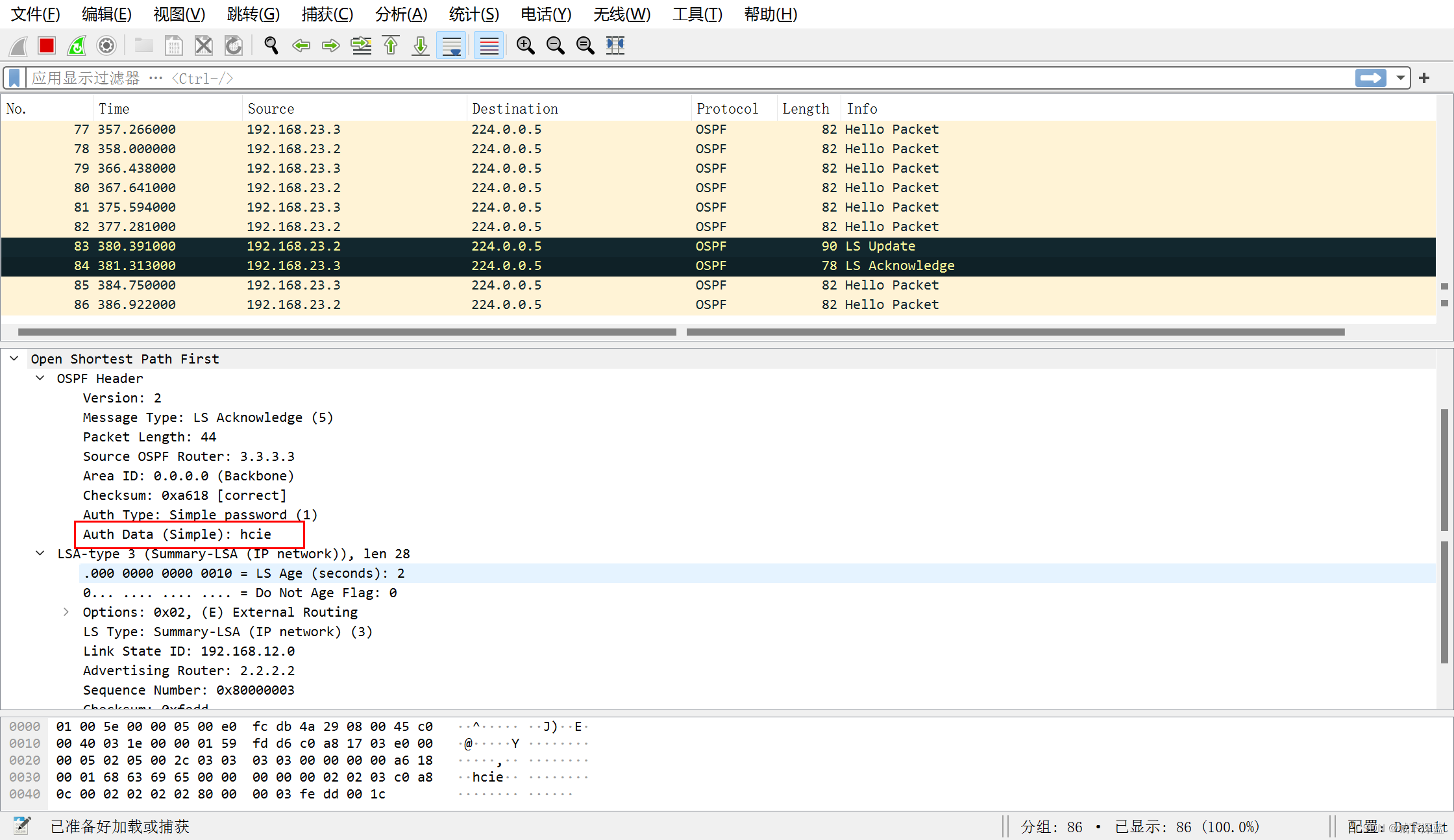
多区域的OSPF实战配置
多区域的OSPF实战配置 需求 如图配置设备的接口IP地址如图规划OSPF网络的区域要求每个设备的 router-id 都是 x.x.x.x(x是每个路由器的名字)确保不同的PC之间可以互通 拓扑图 配置命令 PC1: 192.168.1.1 255.255.255.0 192.168.1.254PC2:…...

现在转行做程序员的多吗?
曾经有一名程序员说,他在编写程序时,就像一个发明家在做实验;当他把程序编好可以运行时,他就已经是个发明家了。 程序员作为众多转行人员首选的职业,也是被大众熟知了。但我们需要知道的不仅是它作为一个职业的定义&a…...
)
社招前端常见react面试题(必备)
解释 React 中 render() 的目的。 每个React组件强制要求必须有一个 render()。它返回一个 React 元素,是原生 DOM 组件的表示。如果需要渲染多个 HTML 元素,则必须将它们组合在一个封闭标记内,例如 <form>、<group>、<div&g…...

力扣-变更性别
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:627. 变更性别二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结前言…...
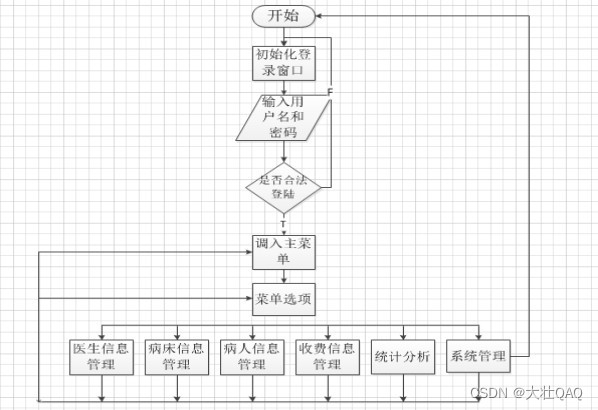
【项目精选】医院管理住院系统的研究与实现(源码+论文+视频)
点击下载源码 本系统主要分为六大模块,分别是医生管理模块、病人管理模块、病床管理模块、收费管理模块、统计分析模块和系统功能模块 ,医生、病人和医院的管理人员都可以通过此系统寻找出自己所需要的信息。 1.1 背景 医院管理住院系统是当今大部分现代…...
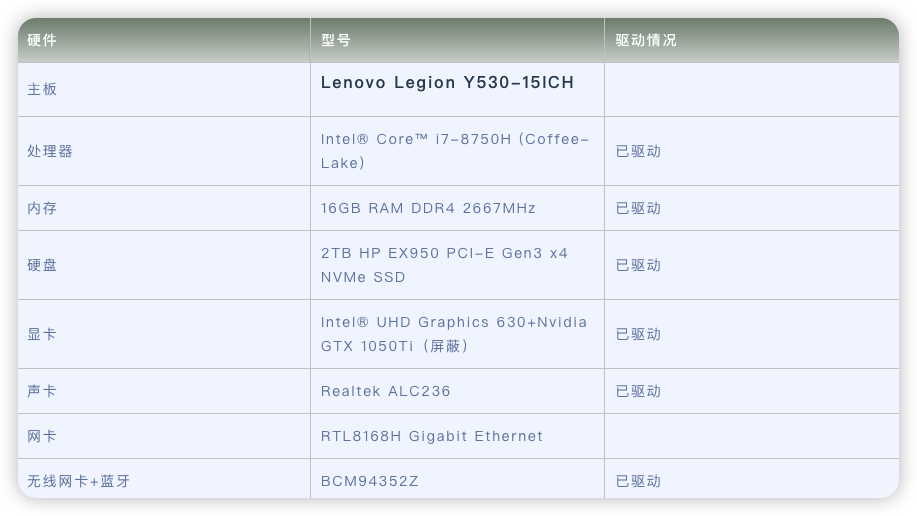
Lenovo Legion Y530-15ICH电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板Lenovo Legion Y530-15ICH处理器Intel Core™ i7-8750H (Coffee-Lake)已驱动内存16GB RAM DDR4 2667MHz已驱动硬盘2TB HP EX950 PCI-E Gen3 x4 NVMe SSD已驱动显卡Intel UHD Graphics 630Nvidia GTX 10…...

CICD 导航
目录内容链接产研服务产研服务参考文章:【产研】 服务部署配置及使用产研服务问题解决参考文章:【问题解决】产研.Net服务部署 配置 使用代码托管GitlabGitlab参考文章:Gitlab 安装 与 使用代码托管Gitlab问题解决参考文章:【问题…...
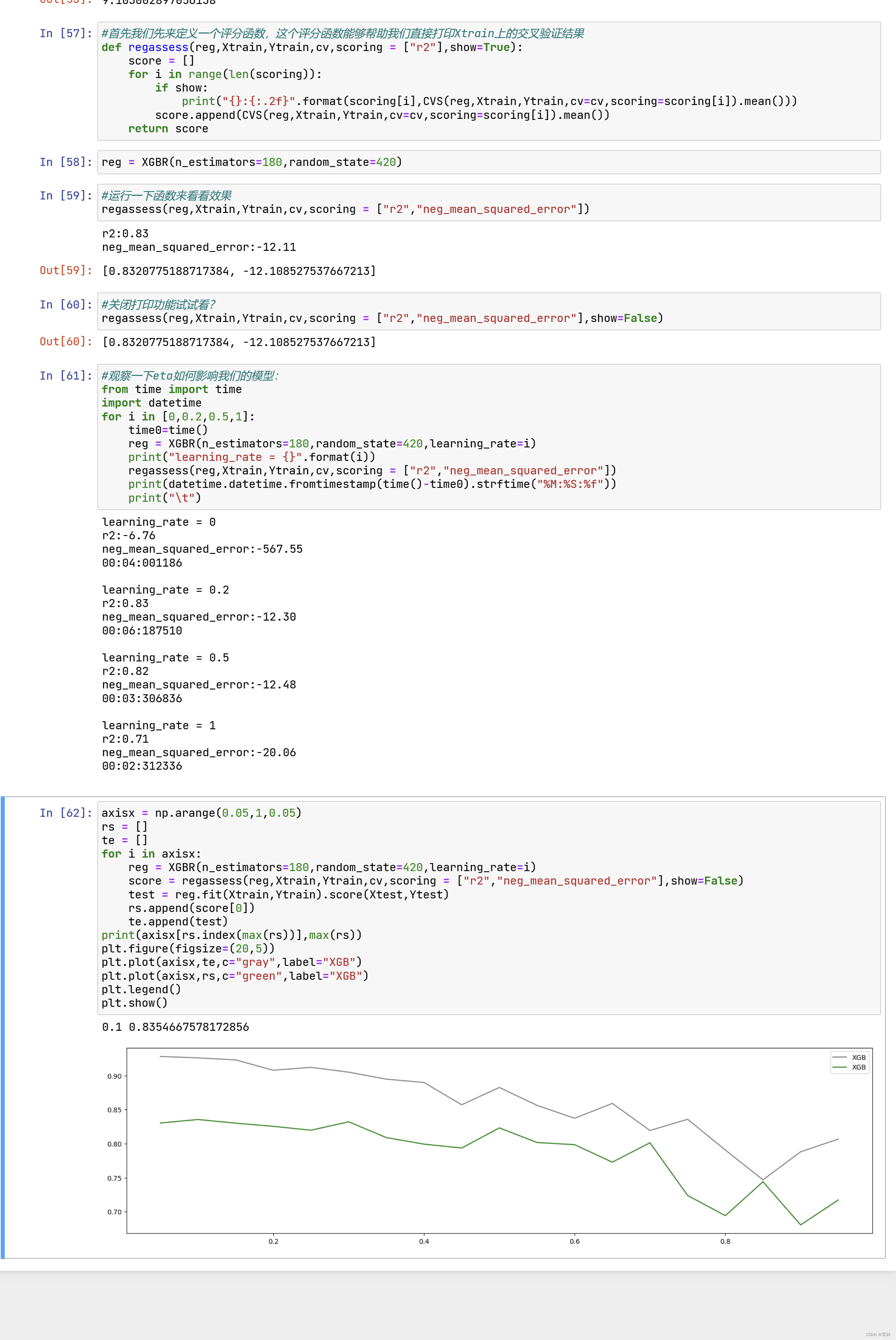
xgboost学习-原理
文章目录一、xgboost库与XGB的sklearn APIXGBoost的三大板块二、梯度提升树提升集成算法:重要参数n_estimators三、有放回随机抽样:重要参数subsample四、迭代决策树:重要参数eta总结一、xgboost库与XGB的sklearn API 现在,我们有…...

如何查看CUDA版本
Linux 查看CUDA版本: nvcc --version或 nvcc --VWindows 查看CUDA版本: nvcc --version或进入 CUDA 的安装目录查看: C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA使用PyTorch 查看 CUDA 版本 import torch print(torch.__ver…...

三、iperf3代码主要架构分析之main函数主要流程
iperf3是一个非常强大的工具,它是用C语言编写的。同时iperf3也是用C语言实现面向对象编程的典范,他以数据结构函数指针为基础,非常好的用C语言实现面向对象的编程的三大特征:封装,继承,多态。相信通过阅读i…...
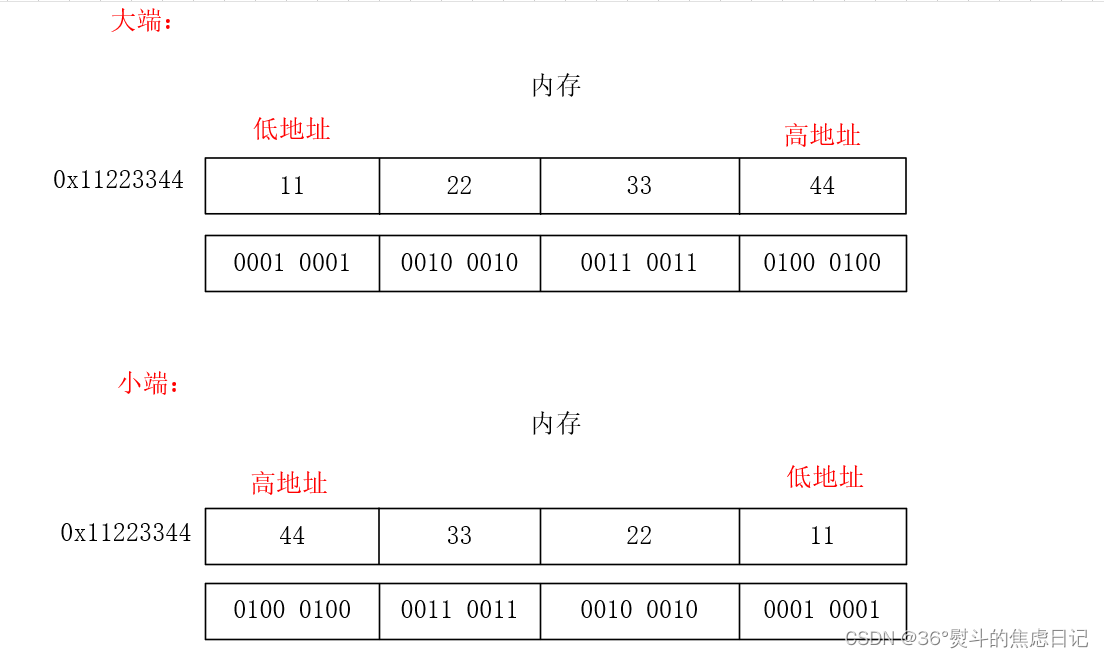
【概念辨析】大小端存储
一、情境 在进行内存调试窗口的查看时,是不是会有一种错觉,就是它存的数据与我们预期的都是颠倒的,比如: 这里的a就和我们预期的不是很相同。 二、大小端 大小端是计算机厂家根据自己的习惯制定的关于数据字节序的规则。 1.大端…...

并发编程-学习总结(下)
目录 1、Future 1.1、Callable和Runnable的不同 1.2、Future的主要功能 1.3、常用方法 1.4、Future使用注意事项 1.5、CompletableFuture(旅游平台问题) 1.5.1、需求 1.5.2、解决方案1:串行 1.5.3、解决方案2:线程池 1.5.4、解决方案3…...

arm汇编指令详细整理及实例详解
目录一、简介二、ARM 汇编指令说明2.1 32位数据操作指令2.2 32位存储器数据传送指令2.3 32位转移指令2.4 其它32位指令三、实例讲解3.1 MRS3.2 MSR3.3 PRIMASK3.4 FAULTMASK3.5 BX指令3.6 零寄存器 wzr、xzr3.7 立即寻址指令3.8 寄存器间接寻址指令3.9 寄存器移位寻址指令3.10 …...
)
高等数学笔记(下下)
无穷级数 定义 一般的,如果给定一个数列u1,u2,u3,...un,...,u_1, u_2, u_3, ... u_n, ... ,u1,u2,u3,...un,...,,那么由这个梳理构成的表达式u1u2u3...un...u_1u_2u_3...u_n...u1u2u3...un...叫做(常数项)无穷级数,简称(常…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
