【算法经典题集】递归(持续更新~~~)
😽PREFACE
🎁欢迎各位→点赞👍 + 收藏⭐ + 评论📝
📢系列专栏:算法经典题集
🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用
💪种一棵树最好是十年前其次是现在
1.递归
1.1 递归实现指数型枚举

下面给出原理分析过程图:
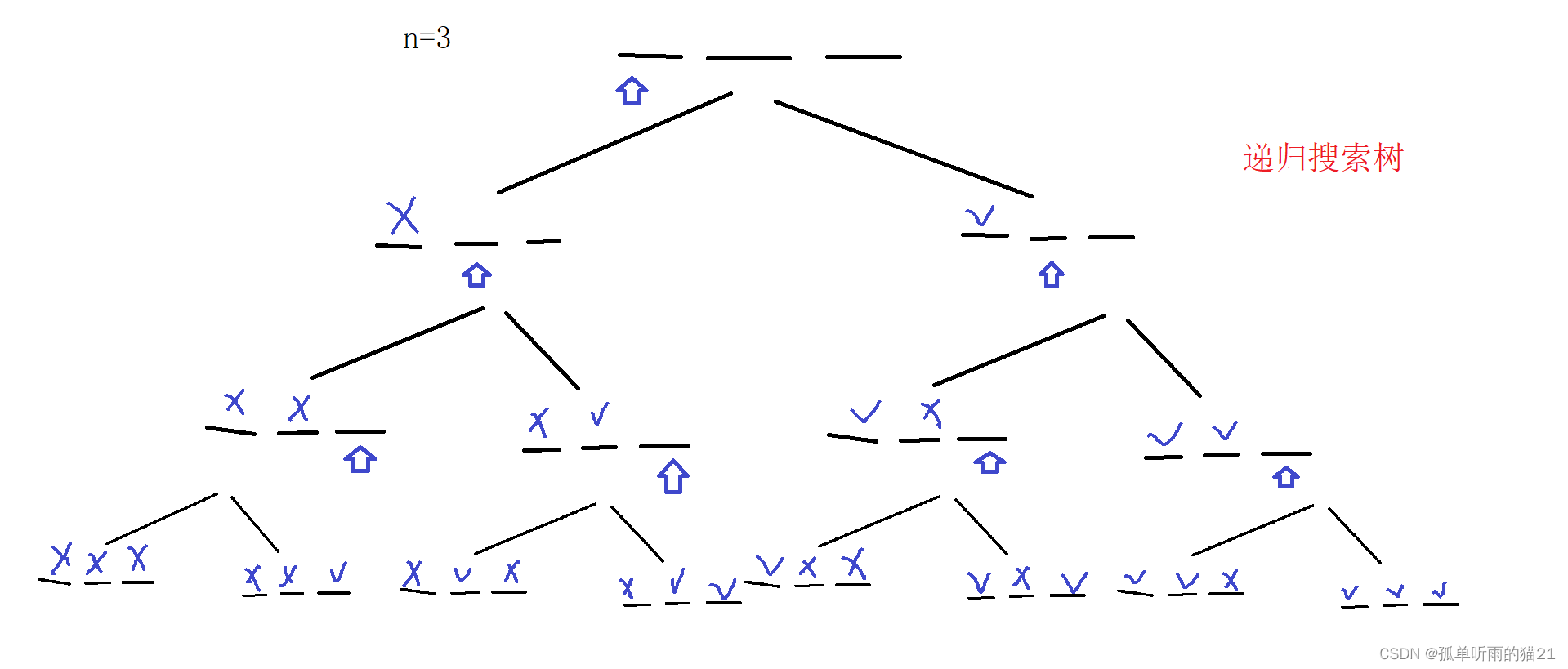
本质就是数学里面的全排列
#include <iostream>
using namespace std;
const int N = 16;
int n;
int st[N];//表示状态:0代表考虑,1代表选择,2代表不选择void dfs(int u)
{if (u > n){for (int i = 1; i <= n; i++){if (st[i] == 1){printf("%d ", i);}}puts("");return;}else{st[u] = 1;//选择dfs(u + 1);st[u] = 0;//回溯st[u] = 2;//不选择dfs(u + 1);st[u] = 0;//回溯}
}int main()
{cin >> n;dfs(1);return 0;
}我们也可以优化一下,不用三个状态去表示,采用bool:
#include <iostream>
using namespace std;
const int N = 16;
int n;
bool vis[N];void dfs(int u)
{if (u > n){for (int i = 1; i <= n; i++){if (vis[i]){printf("%d ", i);}}puts("");return;}else{vis[u] = true;dfs(u + 1);vis[u] = false;dfs(u + 1);}
}int main()
{cin >> n;dfs(1);return 0;
}其实不然,递归顾名思义,先递下去,还要归回来,
针对这里的代码,可能有些人认为不会执行下面的false:

dfs(u+1)运行之后不是还有个return吗,这时候就会返回上一级函数,执行下面的false子任务

回到递归树上对应的父亲节点,接着遍历父亲的其他儿子。他在这颗子树的遍历中,父亲节点选过的打上标记,子节点才不会选。dfs完相当于把这颗树遍历完了,所以这个树又可以选了。
1.2 递归实现排列型枚举

下面给出图解分析过程:
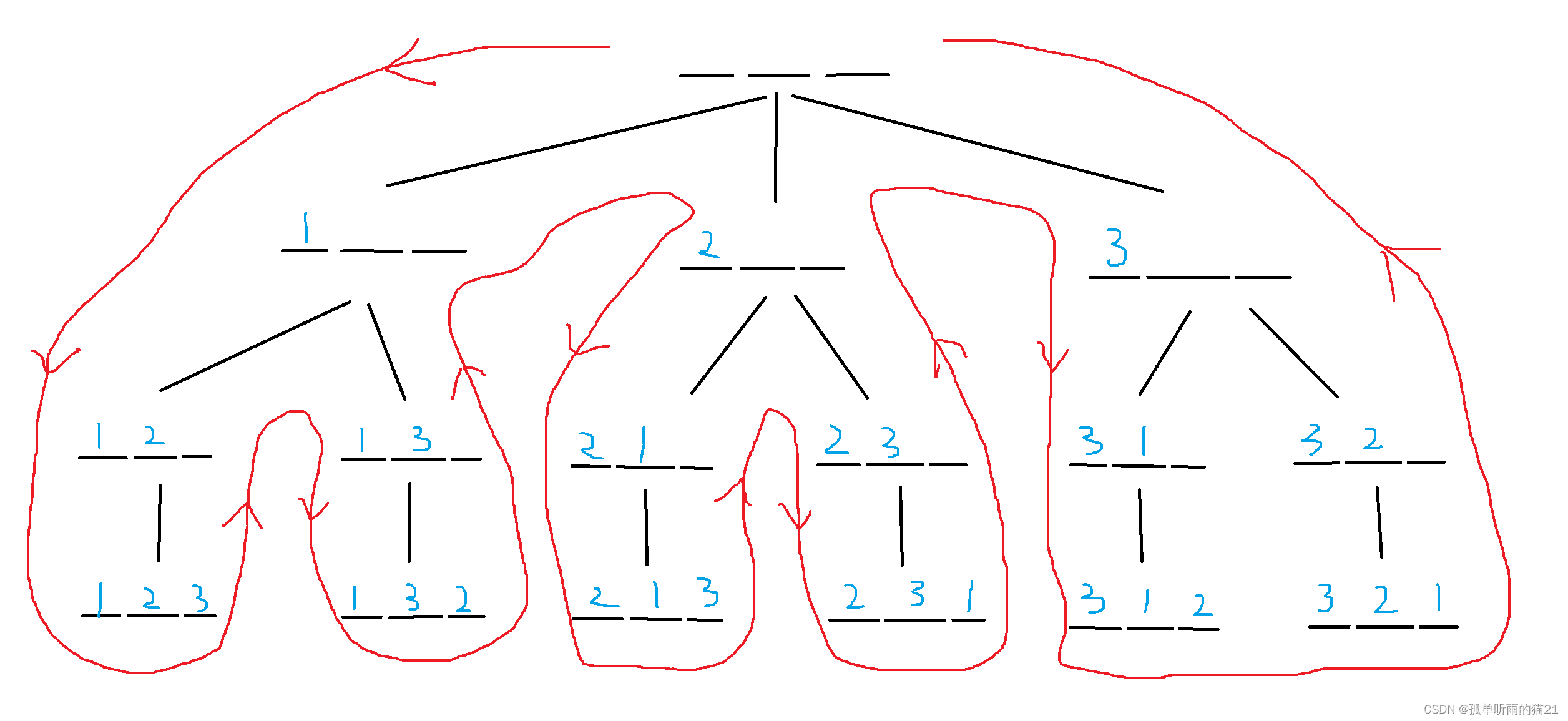
#include <iostream>
using namespace std;
const int N =10;
int path[N];//保存序列
int state[N];//数字是否被使用过
int n;void dfs(int u)
{if(u>n)//数字填完了,输出 {for(int i=1;i<=n;i++)//输出方案 {cout<<path[i]<<" ";}cout<<endl;return ;}else{for(int i=1;i<=n;i++){if(!state[i])//如果数字i没有被用过 {path[u]=i;//放入空位 state[i]=1;//数字被用,修改状态 dfs(u+1);//填下一位 state[i]=0;//回溯,取出i }}}
}int main()
{cin>>n;dfs(1);return 0;
}另外需要注意的是本题的时间复杂度是
下面给出简易的证明:
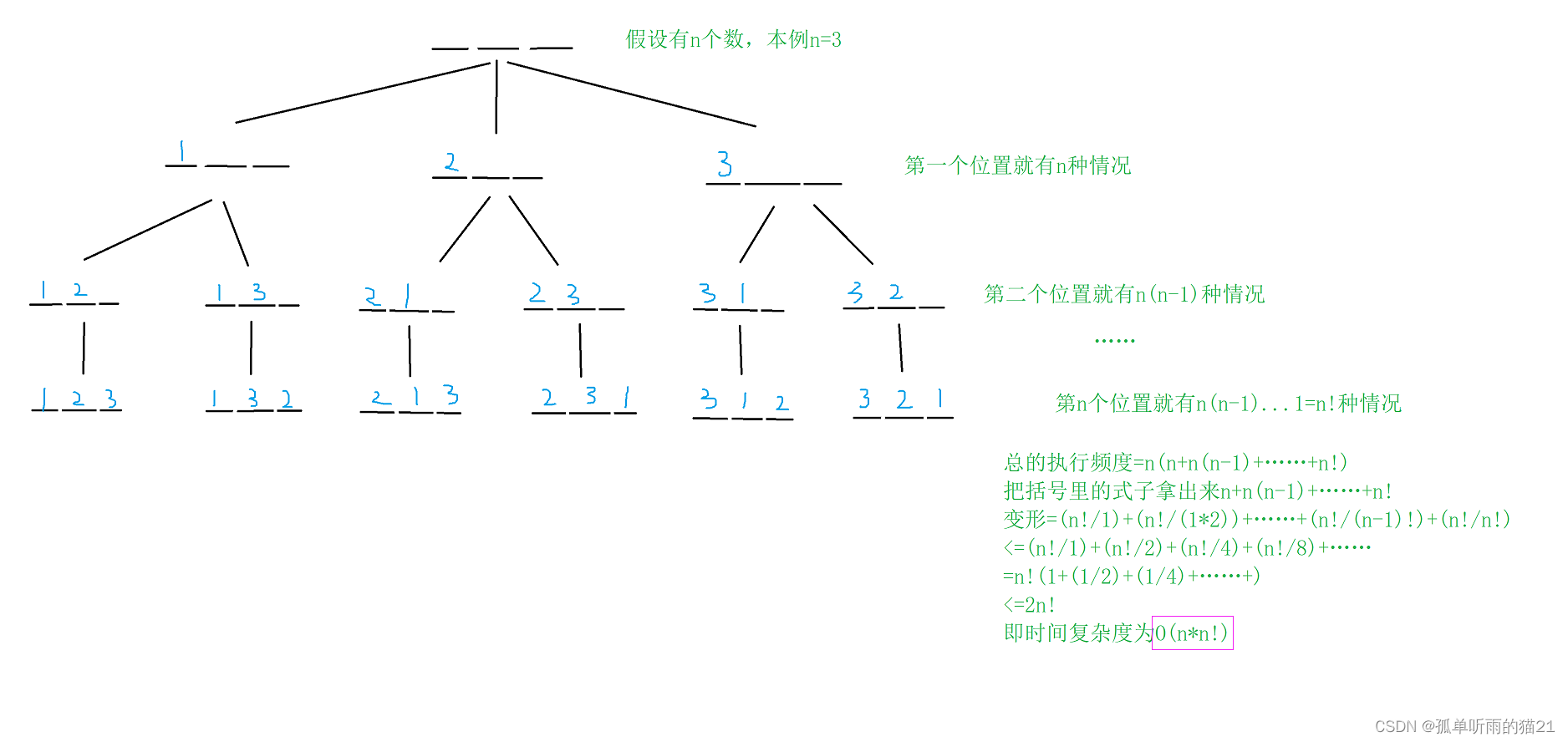
1.3 递归实现组合型枚举

下面给出图解分析过程:
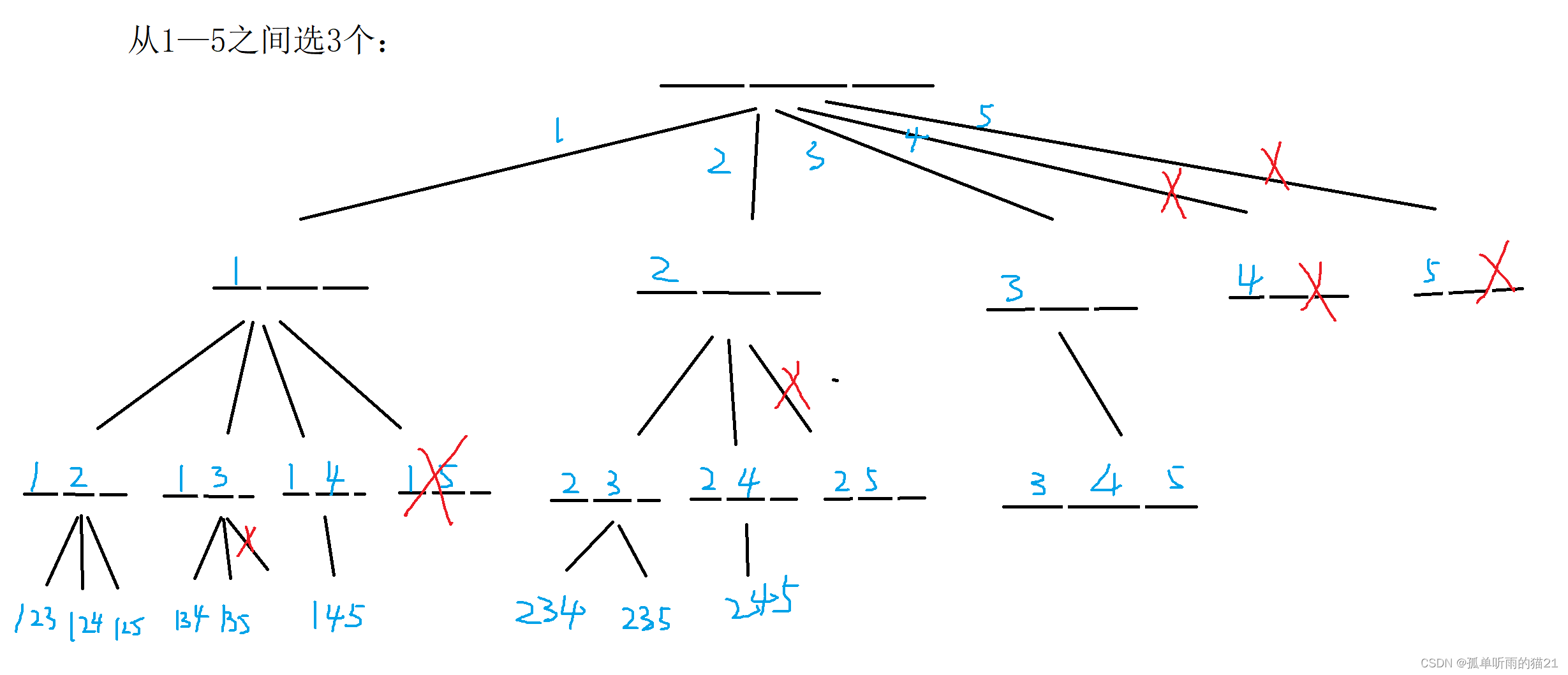
#include <iostream>
using namespace std;
const int N = 30;
int n, m;
int path[N];void dfs(int u, int s)//u代表当前枚举到哪个位置,s代表当前最小可以从哪个数枚举
{if (u + n - s < m) return;//剪枝:就算将剩下的数全部选中也凑不齐m个数,所以一定没有答案,所以减掉if (u == m + 1){for (int i = 1; i <= m; i++) cout << path[i] << " ";puts("");return;}else{for (int i = s; i <= n; i++){path[u] = i;dfs(u + 1, i + 1);path[u] = 0;//回溯}}
}int main()
{cin >> n >> m;dfs(1, 1);return 0;
}1.4 带分数

分析过程:

#include <iostream>
using namespace std;
const int N = 10;
int target;//题目条件给的数
int num[N];//用来保存全排列的结果
bool used[N];//生成全排列的过程中标记是否被使用过
int cnt;//计数,最后的输出结果int calc(int l, int r)//计算num数组中一段的数是多少
{int res = 0;for (int i = l; i <= r; i++){res = res * 10 + num[i];//小学数学的加法进位}return res;
}void dfs(int u)//生成全排列
{if (u == 9){//要把全排列分成三段for (int i = 0; i < 7; i++)//这里的i是位置,跟else里面的i不同{for (int j = i + 1; j < 8; j++){int a = calc(0, i);int b = calc(i + 1, j);int c = calc(j + 1, 8);//这里一定要把除法变成乘法,因为c++里面除法是整除,写成除法的形式容易出错if (c * target == a * c + b){cnt++;}}}return;}else{for (int i = 1; i <= 9; i++)//这里的i是数字{if (!used[i]){used[i] = true;//只要进if里面来,就是标记使用num[u] = i;dfs(u + 1);used[i] = false;//回溯,还原现场}}}
}int main()
{cin >> target;dfs(0);cout << cnt << endl;return 0;
}本题是蓝桥杯某年省赛的原题,下面再给出一个直接调用 next_permutation() 函数的做法,可以代替手写暴搜来枚举全排列,蓝桥杯是可以使用这个函数的
#include <iostream>
#include <algorithm>
using namespace std;const int N = 10;int target;
int num[N];int calc(int l, int r)
{int res = 0;for (int i = l; i <= r; i++){res = res * 10 + num[i];}return res;
}int main()
{cin >> target;for (int i = 0; i < 9; i++) {num[i] = i + 1;}int res = 0;do{for (int i = 0; i < 9; i++) {for (int j = i + 1; j < 9; j++) {int a = calc(0, i);int b = calc(i + 1, j);int c = calc(j + 1, 8);if (a == 0 || b == 0 || c == 0)//特殊情况,需要单独讨论一下{continue;}if (a * c + b == c * target) {++res;}}}// 调用函数生成全排列} while (next_permutation(num, num + 9));cout << res << '\n';return 0;
}为什么 next_permutation() 函数选用do-while循环结构?
因为你初始化的时候数组是一种情况,直接全排列的话第一种情况直接就少掉了。这也是 next_permutation() 的一个固定方式。
补充: next_permutation() 函数
另外补充一下 next_permutation() 函数的用法:
对于next_permutation函数,其函数原型为:
#include <algorithm>
bool next_permutation(iterator start,iterator end)
如果当前序列不存在下一个排列时,函数返回false,否则返回true
例:将1,2,3,4,5进行全排列
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{int num[5] = { 1,2,3,4,5 };do{cout << num[0] << " " << num[1] << " " << num[2] <<" "<<num[3]<<" "<<num[4]<< endl;} while (next_permutation(num, num + 5));return 0;
}如果将+5改为+2:
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{int num[5] = { 1,2,3,4,5 };do{cout << num[0] << " " << num[1] << " " << num[2] <<" "<<num[3]<<" "<<num[4]<< endl;} while (next_permutation(num, num + 2));return 0;
}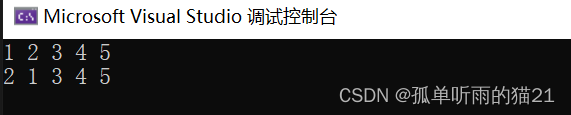
由此可以看出,next_permutation(num,num+n)函数是对数组num中的前n个元素进行全排列,同时并改变num数组的值。
此外,需要强调的是,next_permutation()在使用前需要对欲排列数组按升序排序,否则只能找出该序列之后的全排列数。
相关文章:

【算法经典题集】递归(持续更新~~~)
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法经典题集🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用💪种一棵树最好是十年前其次是现在1.递归1.1 递归实现…...
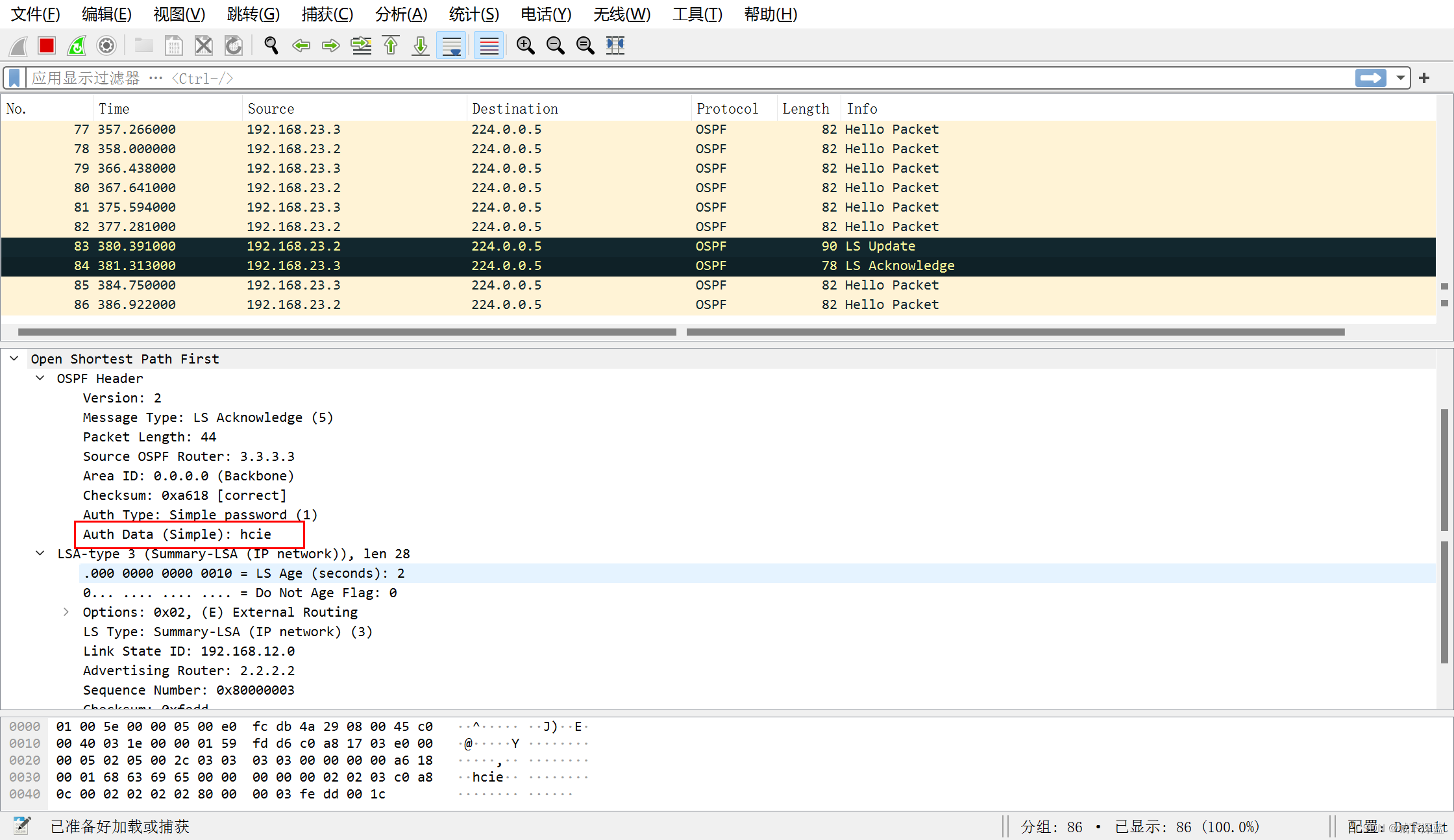
多区域的OSPF实战配置
多区域的OSPF实战配置 需求 如图配置设备的接口IP地址如图规划OSPF网络的区域要求每个设备的 router-id 都是 x.x.x.x(x是每个路由器的名字)确保不同的PC之间可以互通 拓扑图 配置命令 PC1: 192.168.1.1 255.255.255.0 192.168.1.254PC2:…...

现在转行做程序员的多吗?
曾经有一名程序员说,他在编写程序时,就像一个发明家在做实验;当他把程序编好可以运行时,他就已经是个发明家了。 程序员作为众多转行人员首选的职业,也是被大众熟知了。但我们需要知道的不仅是它作为一个职业的定义&a…...
)
社招前端常见react面试题(必备)
解释 React 中 render() 的目的。 每个React组件强制要求必须有一个 render()。它返回一个 React 元素,是原生 DOM 组件的表示。如果需要渲染多个 HTML 元素,则必须将它们组合在一个封闭标记内,例如 <form>、<group>、<div&g…...

力扣-变更性别
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:627. 变更性别二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结前言…...
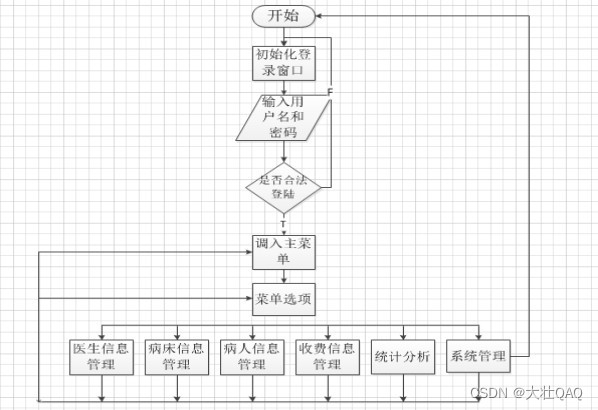
【项目精选】医院管理住院系统的研究与实现(源码+论文+视频)
点击下载源码 本系统主要分为六大模块,分别是医生管理模块、病人管理模块、病床管理模块、收费管理模块、统计分析模块和系统功能模块 ,医生、病人和医院的管理人员都可以通过此系统寻找出自己所需要的信息。 1.1 背景 医院管理住院系统是当今大部分现代…...
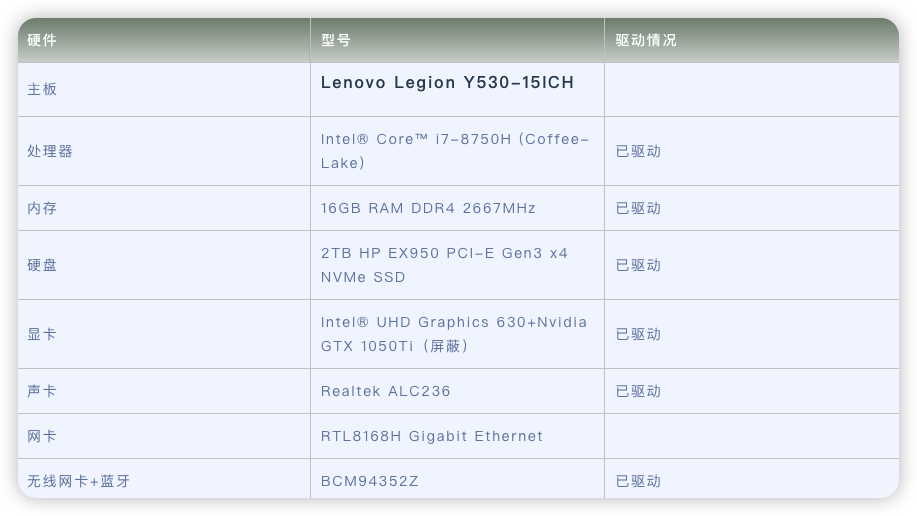
Lenovo Legion Y530-15ICH电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板Lenovo Legion Y530-15ICH处理器Intel Core™ i7-8750H (Coffee-Lake)已驱动内存16GB RAM DDR4 2667MHz已驱动硬盘2TB HP EX950 PCI-E Gen3 x4 NVMe SSD已驱动显卡Intel UHD Graphics 630Nvidia GTX 10…...

CICD 导航
目录内容链接产研服务产研服务参考文章:【产研】 服务部署配置及使用产研服务问题解决参考文章:【问题解决】产研.Net服务部署 配置 使用代码托管GitlabGitlab参考文章:Gitlab 安装 与 使用代码托管Gitlab问题解决参考文章:【问题…...
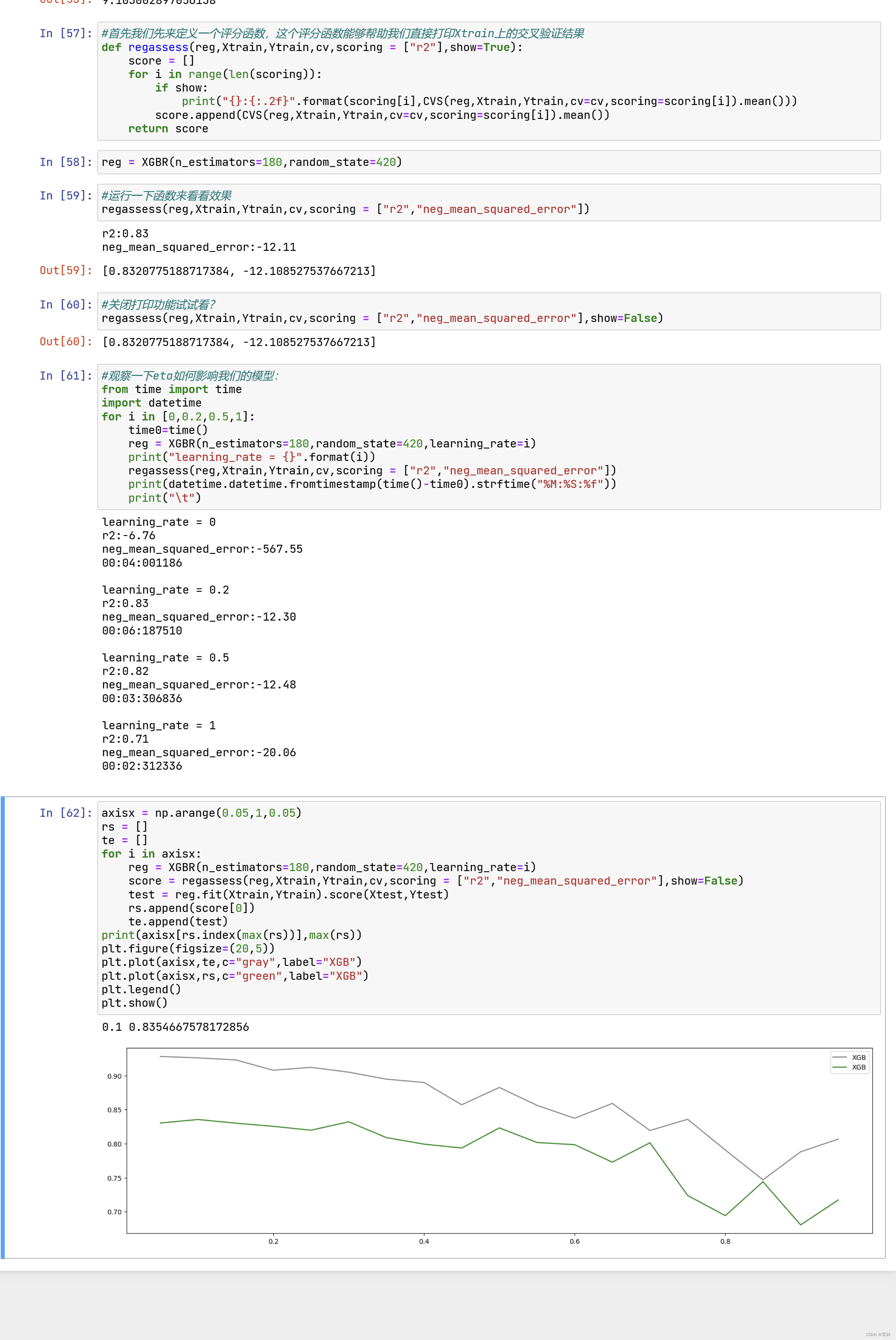
xgboost学习-原理
文章目录一、xgboost库与XGB的sklearn APIXGBoost的三大板块二、梯度提升树提升集成算法:重要参数n_estimators三、有放回随机抽样:重要参数subsample四、迭代决策树:重要参数eta总结一、xgboost库与XGB的sklearn API 现在,我们有…...

如何查看CUDA版本
Linux 查看CUDA版本: nvcc --version或 nvcc --VWindows 查看CUDA版本: nvcc --version或进入 CUDA 的安装目录查看: C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA使用PyTorch 查看 CUDA 版本 import torch print(torch.__ver…...

三、iperf3代码主要架构分析之main函数主要流程
iperf3是一个非常强大的工具,它是用C语言编写的。同时iperf3也是用C语言实现面向对象编程的典范,他以数据结构函数指针为基础,非常好的用C语言实现面向对象的编程的三大特征:封装,继承,多态。相信通过阅读i…...
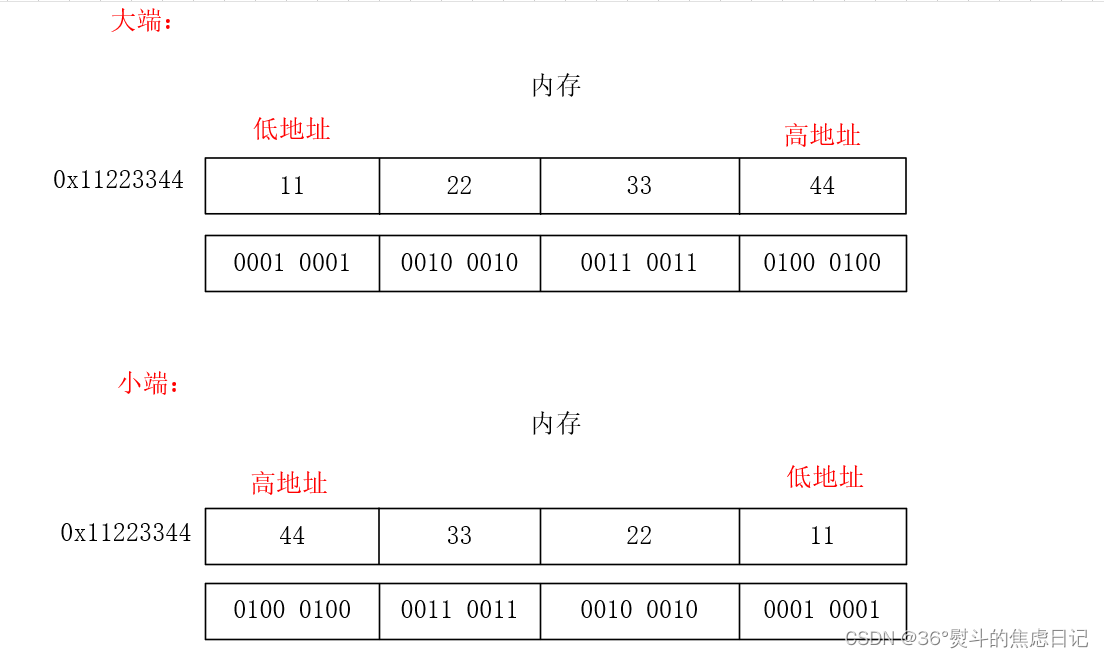
【概念辨析】大小端存储
一、情境 在进行内存调试窗口的查看时,是不是会有一种错觉,就是它存的数据与我们预期的都是颠倒的,比如: 这里的a就和我们预期的不是很相同。 二、大小端 大小端是计算机厂家根据自己的习惯制定的关于数据字节序的规则。 1.大端…...

并发编程-学习总结(下)
目录 1、Future 1.1、Callable和Runnable的不同 1.2、Future的主要功能 1.3、常用方法 1.4、Future使用注意事项 1.5、CompletableFuture(旅游平台问题) 1.5.1、需求 1.5.2、解决方案1:串行 1.5.3、解决方案2:线程池 1.5.4、解决方案3…...

arm汇编指令详细整理及实例详解
目录一、简介二、ARM 汇编指令说明2.1 32位数据操作指令2.2 32位存储器数据传送指令2.3 32位转移指令2.4 其它32位指令三、实例讲解3.1 MRS3.2 MSR3.3 PRIMASK3.4 FAULTMASK3.5 BX指令3.6 零寄存器 wzr、xzr3.7 立即寻址指令3.8 寄存器间接寻址指令3.9 寄存器移位寻址指令3.10 …...
)
高等数学笔记(下下)
无穷级数 定义 一般的,如果给定一个数列u1,u2,u3,...un,...,u_1, u_2, u_3, ... u_n, ... ,u1,u2,u3,...un,...,,那么由这个梳理构成的表达式u1u2u3...un...u_1u_2u_3...u_n...u1u2u3...un...叫做(常数项)无穷级数,简称(常…...
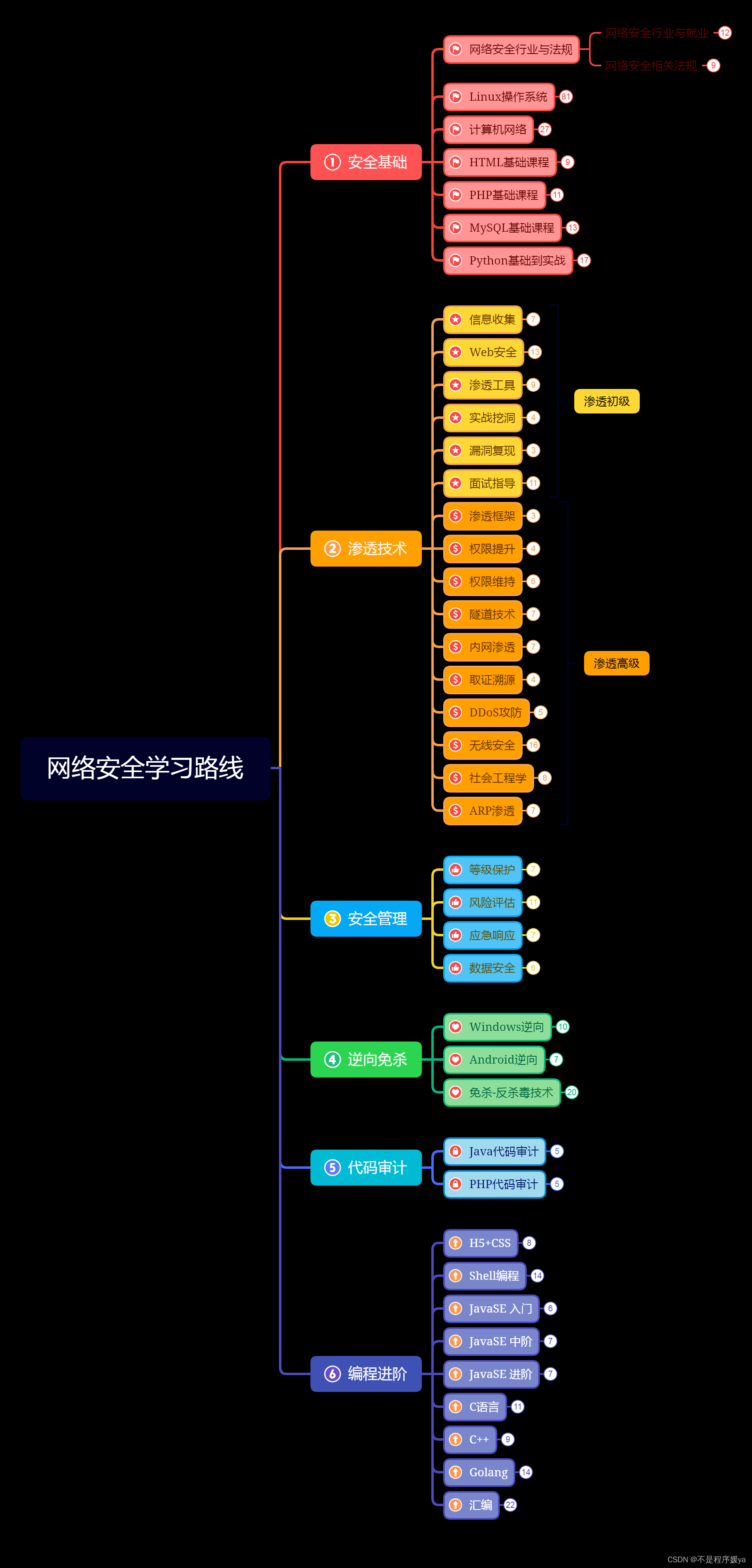
零基础如何入门网络安全(黑客)
我经常会看到这一类的问题: 学习XXX知识没效果;学习XXX技能没方向;学习XXX没办法入门; 给大家一个忠告,如果你完全没有基础的话,前期最好不要盲目去找资料学习,因为大部分人把资料收集好之后&a…...

【C++】map和set用法详解
文章目录1.关联式容器2.键值对3.树形结构的关联式容器3.1 set3.1.1 set的介绍3.1.2 set的模板参数列表3.1.3 set的使用3.2 mapmap的介绍map的模板参数列表map的使用关于map的元素访问总结3.3multimap1.关联式容器 我们接触过STL中的部分容器,比如:vecto…...

BLIP2-图像文本预训练
文章目录摘要解决问题算法模型结构通过frozen图像编码器学习视觉语言表征图像文本对比学习(ITC)基于图像文本生成(ITG)图文匹配(ITM)从大规模语言模型学习视觉到语言生成模型预训练预训练数据预训练图像编码…...
Faster-Rcnn修改转数据集文件
目录 学习python的一些基础知识 argparser assert关键字 让你秒懂Python 类特殊方法__getitem__ lxml.etree.fromstring的使用 统计一下json文件内的种类 正脸红外光 正脸-混合红外光 正脸-交叉偏振光 正脸-平行偏振光 正脸-紫外光 正脸-棕色光 调用mydataset可视化…...
带你沉浸式体验删库跑路
前言:学习的过程比较枯燥,后面会记录一些比较有意思的东西,比如程序员之间流传的删库跑路的梗,当然本次测试是在虚拟机上进行的并进行了快照保护,所以其实没太大问题。首先得要有一个虚拟机要有一个linux iso文件装在虚拟机上以上两点不是本文重点,如果有需要可以私…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
