Linux内核代码中常用的数据结构
Linux内核代码中广泛使用了数据结构和算法,其中最常用的两个是链表和红黑树。
链表
Linux内核代码大量使用了链表这种数据结构。链表是在解决数组不能动态扩展这个缺陷而产生的一种数据结构。链表所包含的元素可以动态创建并插入和删除。
链表的每个元素都是离散存放的,因此不需要占用连续的内存。链表通常由若干节点组成,每个节点的结构都是一样的,由有效数据区和指针区两部分组成。有效数据区用来存储有效数据信息,而指针区用来指向链表的前继节点或者后继节点。因此,链表就是利用指针将各个节点串联起来的一种存储结构。
(1)单向链表
单向链表的指针区只包含一个指向下一个节点的指针,因此会形成一个单一方向的链表,如下代码所示。
struct list {int data; /*有效数据*/struct list *next; /*指向下一个元素的指针*/
};
如图所示,单向链表具有单向移动性,也就是只能访问当前的节点的后继节点,而无法访问当前节点的前继节点,因此在实际项目中运用得比较少。

单向链表示意图
(2)双向链表
如图所示,双向链表和单向链表的区别是指针区包含了两个指针,一个指向前继节点,另一个指向后继节点,如下代码所示。
struct list {int data; /*有效数据*/struct list *next; /*指向下一个元素的指针*/struct list *prev; /*指向上一个元素的指针*/
};
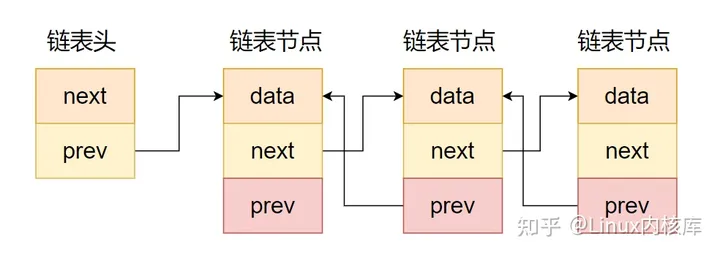
双向链表示意图(链表头应该是next指向节点)
(3)Linux内核链表实现
单向链表和双向链表在实际使用中有一些局限性,如数据区必须是固定数据,而实际需求是多种多样的。这种方法无法构建一套通用的链表,因为每个不同的数据区需要一套链表。
为此,Linux内核把所有链表操作方法的共同部分提取出来,把不同的部分留给代码编程者自己去处理。
Linux内核实现了一套纯链表的封装,链表节点数据结构只有指针区而没有数据区,另外还封装了各种操作函数,如创建节点函数、插入节点函数、删除节点函数、遍历节点函数等。
Linux内核链表使用 struct list_head 数据结构来描述。
<include/linux/types.h>struct list_head {struct list_head *next, *prev;
};
struct list_head数据结构不包含链表节点的数据区,通常是嵌入其他数据结构,如struct page数据结构中嵌入了一个lru链表节点,通常是把page数据结构挂入LRU链表。
<include/linux/mm_types.h>struct page {...struct list_head lru;...
}
链表头的初始化有两种方法,一种是静态初始化,另一种动态初始化。
把next和prev指针都初始化并指向自己,这样便初始化了一个带头节点的空链表。
<include/linux/list.h>/*静态初始化*/
#define LIST_HEAD_INIT(name) { &(name), &(name) }#define LIST_HEAD(name) \struct list_head name = LIST_HEAD_INIT(name)/*动态初始化*/
static inline void INIT_LIST_HEAD(struct list_head *list)
{list->next = list;list->prev = list;
}
添加节点到一个链表中,内核提供了几个接口函数,如list_add()是把一个节点添加到表头,list_add_tail()是插入表尾。
<include/linux/list.h>void list_add(struct list_head *new, struct list_head *head)
list_add_tail(struct list_head *new, struct list_head *head)
遍历节点的接口函数。
#define list_for_each(pos, head) \
for (pos = (head)->next; pos != (head); pos = pos->next)
这个宏只是遍历一个一个节点的当前位置,那么如何获取节点本身的数据结构呢?这里还需要使用list_entry()宏。
#define list_entry(ptr, type, member) \container_of(ptr, type, member)
//container_of()宏的定义在kernel.h头文件中。
#define container_of(ptr, type, member) ({ \const typeof( ((type *)0)->member ) *__mptr = (ptr); \(type *)( (char *)__mptr - offsetof(type,member) );})#define offsetof(TYPE, MEMBER) ((size_t) &((TYPE *)0)->MEMBER)
其中offsetof()宏是通过把0地址转换为type类型的指针,然后去获取该结构体中member成员的指针,也就是获取了member在type结构体中的偏移量。最后用指针ptr减去offset,就得到type结构体的真实地址了。
下面是遍历链表的一个例子。
<drivers/block/osdblk.c>static ssize_t class_osdblk_list(struct class *c,struct class_attribute *attr,char *data)
{int n = 0;struct list_head *tmp;list_for_each(tmp, &osdblkdev_list) {struct osdblk_device *osdev;osdev = list_entry(tmp, struct osdblk_device, node);n += sprintf(data+n, "%d %d %llu %llu %s\n",osdev->id,osdev->major,osdev->obj.partition,osdev->obj.id,osdev->osd_path);}return n;
}
红黑树
红黑树(Red Black Tree)被广泛应用在内核的内存管理和进程调度中,用于将排序的元素组织到树中。红黑树被广泛应用在计算机科学的各个领域中,它在速度和实现复杂度之间提供一个很好的平衡。
红黑树是具有以下特征的二叉树:
- 每个节点或红或黑。
- 每个叶节点是黑色的。
- 如果结点都是红色,那么两个子结点都是黑色。
- 从一个内部结点到叶结点的简单路径上,对所有叶节点来说,黑色结点的数目都是相同的。
红黑树的一个优点是,所有重要的操作(例如插入、删除、搜索)都可以在O(log n)时间内完成,n为树中元素的数目。
经典的算法教科书都会讲解红黑树的实现,这里只是列出一个内核中使用红黑树的例子,供读者在实际的驱动和内核编程中参考。这个例子可以在内核代码的documentation/Rbtree.txt文件中找到。
#include <linux/init.h>
#include <linux/list.h>
#include <linux/module.h>
#include <linux/kernel.h>
#include <linux/slab.h>
#include <linux/mm.h>
#include <linux/rbtree.h>MODULE_AUTHOR("figo.zhang");
MODULE_DESCRIPTION(" ");
MODULE_LICENSE("GPL");struct mytype { struct rb_node node;int key;
};/*红黑树根节点*/struct rb_root mytree = RB_ROOT;
/*根据key来查找节点*/
struct mytype *my_search(struct rb_root *root, int new){struct rb_node *node = root->rb_node;while (node) {struct mytype *data = container_of(node, struct mytype, node);if (data->key > new)node = node->rb_left;else if (data->key < new)node = node->rb_right;elsereturn data;}return NULL;}/*插入一个元素到红黑树中*/int my_insert(struct rb_root *root, struct mytype *data){struct rb_node **new = &(root->rb_node), *parent=NULL;/* 寻找可以添加新节点的地方 */while (*new) {struct mytype *this = container_of(*new, struct mytype, node);parent = *new;if (this->key > data->key)new = &((*new)->rb_left);else if (this->key < data->key) {new = &((*new)->rb_right);} elsereturn -1;}/* 添加一个新节点 */rb_link_node(&data->node, parent, new);rb_insert_color(&data->node, root);return 0;}static int __init my_init(void)
{int i;struct mytype *data;struct rb_node *node;/*插入元素*/for (i =0; i < 20; i+=2) {data = kmalloc(sizeof(struct mytype), GFP_KERNEL);data->key = i;my_insert(&mytree, data);}/*遍历红黑树,打印所有节点的key值*/for (node = rb_first(&mytree); node; node = rb_next(node)) printk("key=%d\n", rb_entry(node, struct mytype, node)->key);return 0;
}static void __exit my_exit(void)
{struct mytype *data;struct rb_node *node;for (node = rb_first(&mytree); node; node = rb_next(node)) {data = rb_entry(node, struct mytype, node);if (data) {rb_erase(&data->node, &mytree);kfree(data);}}
}
module_init(my_init);
module_exit(my_exit);
mytree是红黑树的根节点,my_insert()实现插入一个元素到红黑树中,my_search()根据key来查找节点。内核大量使用红黑树,如虚拟地址空间VMA的管理。
资料直通车:Linux内核源码技术学习路线+视频教程内核源码
学习直通车:Linuxc/c++高级开发【直播公开课】
零声白金VIP体验卡:零声白金VIP体验卡(含基础架构/高性能存储/golang/QT/音视频/Linux内核)
无锁环形缓冲区
生产者和消费者模型是计算机编程中最常见的一种模型。生产者产生数据,而消费者消耗数据,如一个网络设备,硬件设备接收网络包,然后应用程序读取网络包。
环形缓冲区是实现生产者和消费者模型的经典算法。环形缓冲区通常有一个读指针和一个写指针。读指针指向环形缓冲区中可读的数据,写指针指向环形缓冲区可写的数据。通过移动读指针和写指针实现缓冲区数据的读取和写入。
在Linux内核中,KFIFO是采用无锁环形缓冲区的实现。FIFO的全称是“First In First Out”,即先进先出的数据结构,它采用环形缓冲区的方法来实现,并提供一个无边界的字节流服务。
采用环形缓冲区的好处是,当一个数据元素被消耗之后,其余数据元素不需要移动其存储位置,从而减少复制,提高效率。
(1)创建KFIFO
在使用KFIFO之前需要进行初始化,这里有静态初始化和动态初始化两种方式。
<include/linux/kfifo.h>int kfifo_alloc(fifo, size, gfp_mask)
该函数创建并分配一个大小为size的KFIFO环形缓冲区。第一个参数fifo是指向该环形缓冲区的struct kfifo数据结构;第二个参数size是指定缓冲区元素的数量;第三个参数gfp_mask表示分配KFIFO元素使用的分配掩码。
静态分配可以使用如下的宏。
#define DEFINE_KFIFO(fifo, type, size)
#define INIT_KFIFO(fifo)
(2)入列
把数据写入KFIFO环形缓冲区可以使用kfifo_in()函数接口。
int kfifo_in(fifo, buf, n)
该函数把buf指针指向的n个数据复制到KFIFO环形缓冲区中。第一个参数fifo指的是KFIFO环形缓冲区;第二个参数buf指向要复制的数据的buffer;第三个数据是要复制数据元素的数量。
(3)出列
从KFIFO环形缓冲区中列出或者摘取数据可以使用kfifo_out()函数接口。
#define kfifo_out(fifo, buf, n)
该函数是从fifo指向的环形缓冲区中复制n个数据元素到buf指向的缓冲区中。如果KFIFO环形缓冲区的数据元素小于n个,那么复制出去的数据元素小于n个。
(4)获取缓冲区大小
KFIFO提供了几个接口函数来查询环形缓冲区的状态。
#define kfifo_size(fifo)
#define kfifo_len(fifo)
#define kfifo_is_empty(fifo)
#define kfifo_is_full(fifo)
kfifo_size()用来获取环形缓冲区的大小,也就是最大可以容纳多少个数据元素。kfifo_len()用来获取当前环形缓冲区中有多少个有效数据元素。kfifo_is_empty()判断环形缓冲区是否为空。kfifo_is_full()判断环形缓冲区是否为满。
(5)与用户空间数据交互
KFIFO还封装了两个函数与用户空间数据交互。
#define kfifo_from_user(fifo, from, len, copied)
#define kfifo_to_user(fifo, to, len, copied)
kfifo_from_user()是把from指向的用户空间的len个数据元素复制到KFIFO中,最后一个参数copied表示成功复制了几个数据元素。
kfifo_to_user()则相反,把KFIFO的数据元素复制到用户空间。这两个宏结合了copy_to_user()、copy_from_user()以及KFIFO的机制,给驱动开发者提供了方便。
相关文章:

Linux内核代码中常用的数据结构
Linux内核代码中广泛使用了数据结构和算法,其中最常用的两个是链表和红黑树。 链表 Linux内核代码大量使用了链表这种数据结构。链表是在解决数组不能动态扩展这个缺陷而产生的一种数据结构。链表所包含的元素可以动态创建并插入和删除。 链表的每个元素都是离散…...

自动驾驶,从“宠儿”走进“淘汰赛”
从“一步到位”到场景、技术降维。从拼落地路径,到拼雷达、算力,再到如今的性价比之争,自动驾驶似乎变得愈发“接地气”。 作者|斗斗 编辑|皮爷 出品|产业家 比起去年,黄文欢和张放今年显得更加忙碌。 “自动驾驶赛道&…...

Tensorflow2 中模型训练标签顺序和预测结果标签顺序不一致问题解决办法
本篇文章将详细介绍Tensorflow2.x中模型训练标签顺序和预测结果标签顺序不一致问题,这个问题如果考虑不周,或者标签顺序没有控制好的情况下会出现预测结果精度极其不准确的情况。 训练数据集的结构:数据集有超过10的类别数,这里包…...
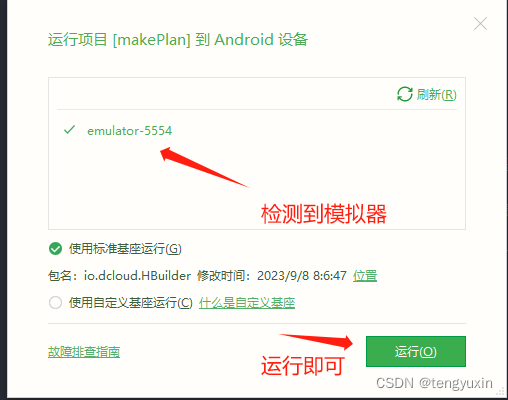
uniapp 在 Android Studio 模拟器中运行项目
在开发App时,无论是使用 Flutter 还是 React native,还是使用uni-app 开发跨端App时,总是需要运行调试。一般调试分为两种。 第一:真机调试 第二:模拟器调试 真机调试的好处是可以看到更好的效果,缺点就是…...

淘宝API接口获取商品信息,订单管理,库存管理,数据分析
在淘宝开放平台中,每个API接口都有相应的文档说明和授权机制,以确保数据的安全性和可靠性。开发者可以根据自己的需求选择相应的API接口,并根据文档说明进行调用和使用。 淘宝开放平台API接口是一套REST方式的开放应用程序编程接口&…...

Azure - 机器学习企业级服务概述与介绍
目录 一、什么是 Azure 机器学习?大规模生成业务关键型机器学习模型 二、Azure 机器学习适合哪些人群?三、Azure 机器学习的价值点加快价值实现速度协作并简化 MLOps信心十足地开发负责任地设计 四、端到端机器学习生命周期的支持准备数据生成和训练模型…...

Linux docker 安装 部署
docker 安装 linux系统离线安装docker 如何使用docker部署c/c程序 常用命令 给予 docker 访问 gui 的权限 在 /etc/profile 末尾添加 if [ "$DISPLAY" ! "" ] thenxhost fi在执行 更新 source /etc/profiledocker下载镜像 docker search gcc #搜索d…...

selenium+python web自动化测试框架项目实战实例教程
自动化测试对程序的回归测试更方便。 由于回归测试的动作和用例是完全设计好的,测试期望的结果也是完全可以预料的,将回归测试自动运行... 可以运行更加繁琐的测试 自动化测试的一个明显好处就是可以在很短的时间内运行更多的测试。学习自动化测试最终目的是应用到实际项目中&…...

软考高级系统架构设计师系列之:案例分析典型试题七
软考高级系统架构设计师系列之:案例分析典型试题七 一、架构评估1.案例试题2.参考答案一、架构评估 某网上购物电子商务公司拟升级正在使用的在线交易系统,以提高用户网上购物在线支付环节的效率和安全性。在系统的需求分析与架构设计阶段,公司提出的需求和关键质量属性场景…...
【算法|动态规划No30】leetcode5. 最长回文子串
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

计算机视觉 激光雷达结合无监督学习进行物体检测的工作原理
一、简述 激光雷达是目前正在改变世界的传感器。它集成在自动驾驶汽车、自主无人机、机器人、卫星、火箭等中。该传感器使用激光束了解世界,并测量激光击中目标返回所需的时间,输出是点云信息,利用这些信息,我们可以从3D点云中查找障碍物。 从自动驾驶汽车的角度看激光雷达…...
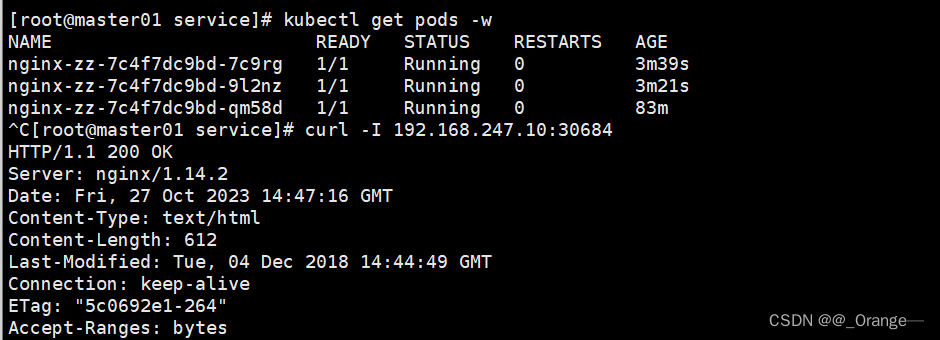
kubectl资源管理命令-陈述式
目录 一、陈述式对象管理 1、基本概念 2、基础命令使用 3、基本信息查看(kubectl get) 4、增删等操作 5、登录pod中的容器 6、扩容缩容pod控制器的pod 7、删除副本控制器 二、创建项目实例 1、创建 kubectl create命令 2、发布 kubectl …...
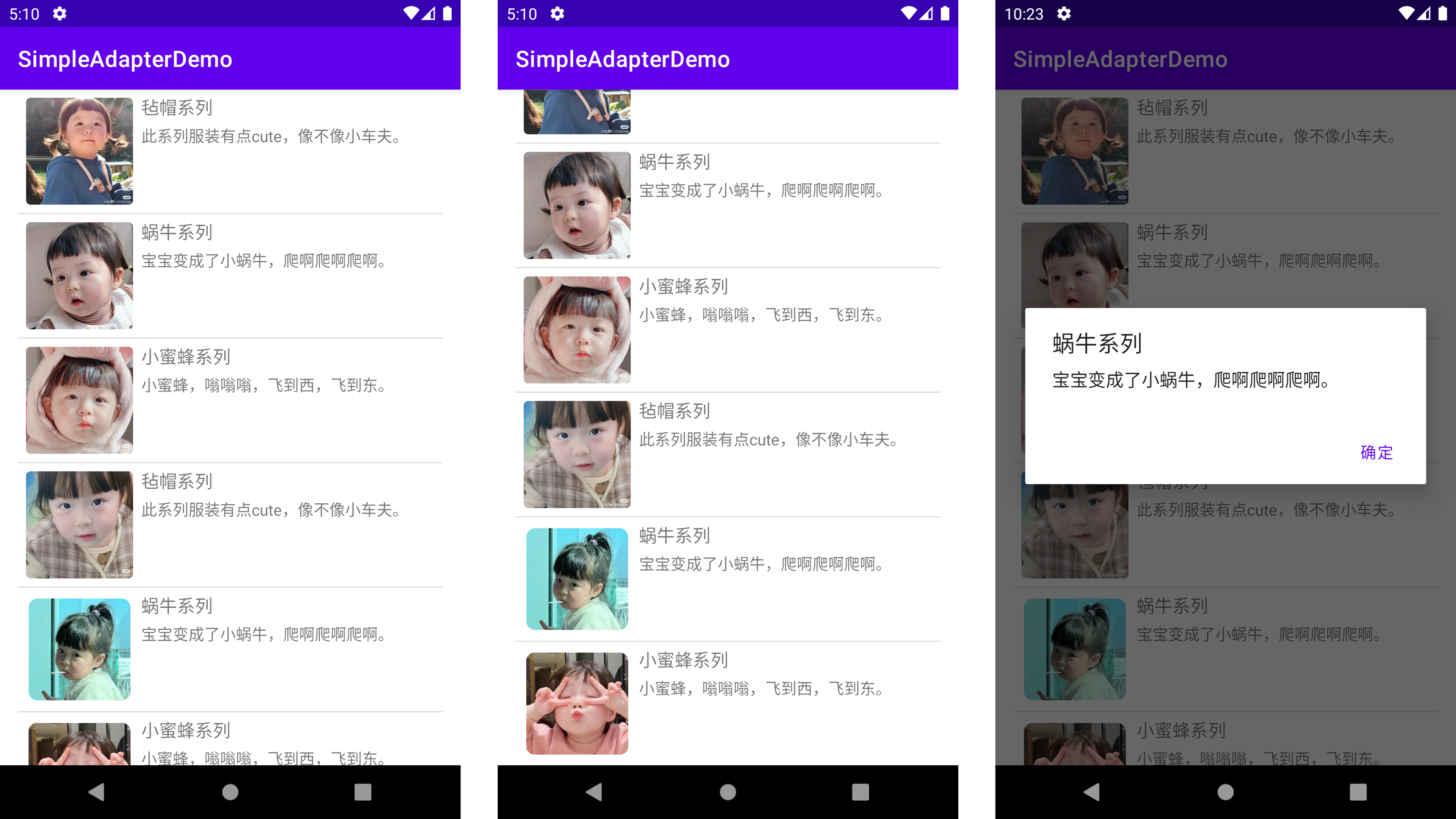
Android-宝宝相册(第四次作业)
第四次作业-宝宝相册 题目 用Listview建立宝宝相册,相册内容及图片可自行设定,也可在资料文件中获取。给出模拟器仿真界面及代码截图。 (参考例4-8) 创建工程项目 创建名为baby的项目工程,最后的工程目录结构如下图所…...

Android应用:实现网络加载商品数据【OKHttp、Glide、Gson】
实现网络加载商品数据的功能: 1、在AndroidManifest.xml中声明网络权限; 2、在app/build.gradle中添加okhttp, glide, gson等必需的第3方库; 3、在MainActivity中通过OkHttpClient连接给定的Web服务,获取商品数据;对…...

增强常见问题解答搜索引擎:在 Elasticsearch 中利用 KNN 的力量
在快速准确的信息检索至关重要的时代,开发强大的搜索引擎至关重要。 随着大型语言模型和信息检索架构(如 RAG)的出现,在现代软件系统中利用文本表示(向量/嵌入)和向量数据库已变得越来越流行。 在本文中&am…...
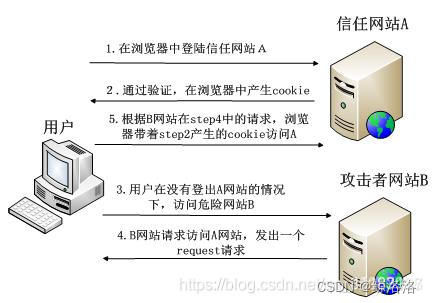
常见网络攻击及防御方法总结(XSS、SQL注入、CSRF攻击)
网络攻击无时无刻不存在,其中XSS攻击和SQL注入攻击是网站应用攻击的最主要的两种手段,全球大约70%的网站应用攻击都来自XSS攻击和SQL注入攻击。此外,常用的网站应用攻击还包括CSRF、Session劫持等。 1、 XSS攻击 XSS攻击即跨站点脚本攻击&am…...

python爬虫request和BeautifulSoup使用
request使用 1.安装request pip install request2.引入库 import requests3.编写代码 发送请求 我们通过以下代码可以打开豆瓣top250的网站 response requests.get(f"https://movie.douban.com/top250")但因为该网站加入了反爬机制,所以…...

记录--vue3实现excel文件预览和打印
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 前言 在前端开发中,有时候一些业务场景中,我们有需求要去实现excel的预览和打印功能,本文在vue3中如何实现Excel文件的预览和打印。 预览excel 关于实现excel文档在…...
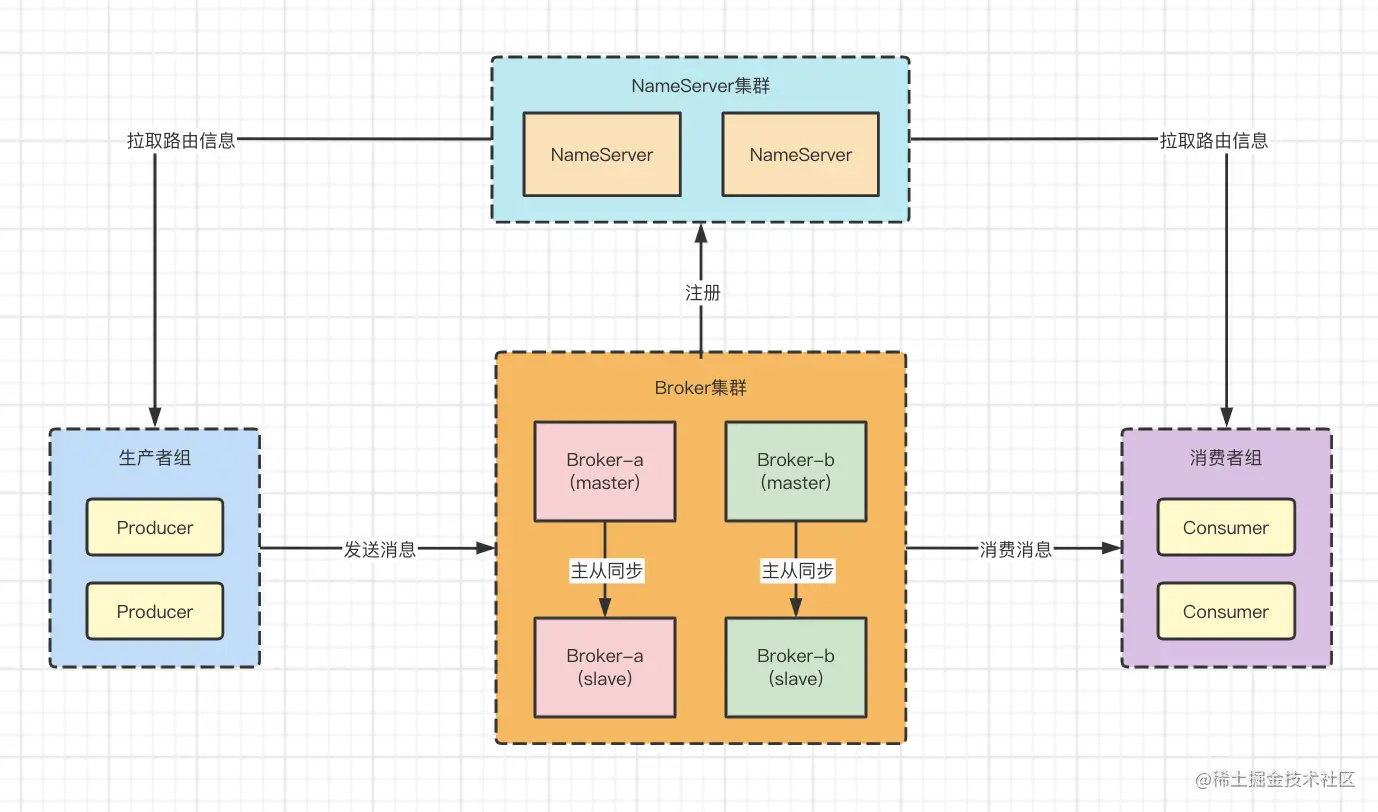
消息队列中间件面试笔记总结RabbitMQ,Kafka,RocketMQ
文章目录 (一) Rabbit MQRabbitMQ 核心概念消息队列的作用Exchange(交换器)Broker(消息中间件的服务节点)如何保证消息的可靠性如何保证 RabbitMQ 消息的顺序性如何保证 RabbitMQ 高可用的?如何解决消息队列的延时以及过期失效问题消息堆积问…...
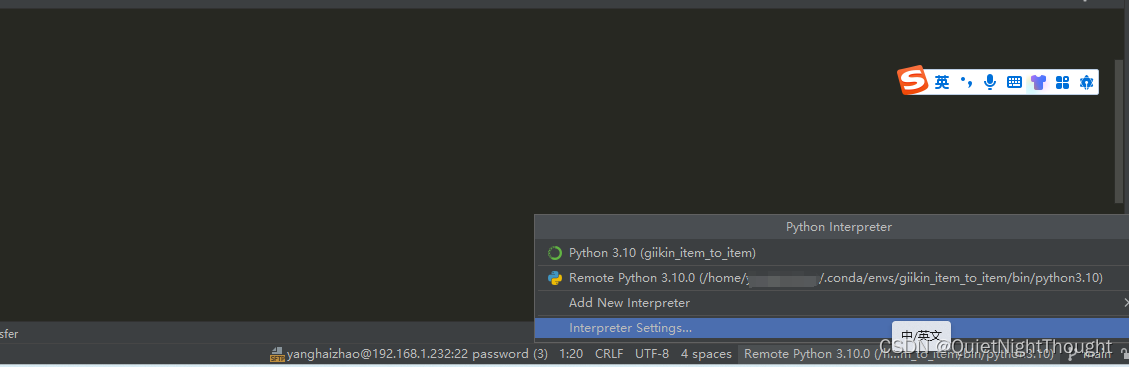
pycharm远程连接Linux服务器
文章目录 一:说明二:系统三:实现远程连接方式一: 直接连接服务器不使用服务器的虚拟环境步骤一:找到配置服务器的地方步骤二:进行连接配置步骤三:进行项目文件映射操作步骤四:让文件…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
