LeetCode 2558. 从数量最多的堆取走礼物【模拟,堆或原地堆化】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个整数数组 gifts ,表示各堆礼物的数量。每一秒,你需要执行以下操作:
- 选择礼物数量最多的那一堆。
- 如果不止一堆都符合礼物数量最多,从中选择任一堆即可。
- 选中的那一堆留下平方根数量的礼物(向下取整),取走其他的礼物。
返回在 k 秒后剩下的礼物数量。
示例 1:
输入:gifts = [25,64,9,4,100], k = 4
输出:29
解释:
按下述方式取走礼物:
- 在第一秒,选中最后一堆,剩下 10 个礼物。
- 接着第二秒选中第二堆礼物,剩下 8 个礼物。
- 然后选中第一堆礼物,剩下 5 个礼物。
- 最后,再次选中最后一堆礼物,剩下 3 个礼物。
最后剩下的礼物数量分别是 [5,8,9,4,3] ,所以,剩下礼物的总数量是 29 。
示例 2:
输入:gifts = [1,1,1,1], k = 4
输出:4
解释:
在本例中,不管选中哪一堆礼物,都必须剩下 1 个礼物。
也就是说,你无法获取任一堆中的礼物。
所以,剩下礼物的总数量是 4 。
提示:
1 <= gifts.length <= 10^31 <= gifts[i] <= 10^91 <= k <= 10^3
相似题目:
- 2558. 从数量最多的堆取走礼物
- 2530. 执行 K 次操作后的最大分数
- 1962. 移除石子使总数最小
- 2208. 将数组和减半的最少操作次数
- 2233. K 次增加后的最大乘积
解法 模拟+堆
维护一些数的最大值,可以最大堆模拟。循环 k k k 次。每次循环,弹出堆顶 top \textit{top} top ,然后把 ⌊ top ⌋ \left\lfloor\sqrt{\textit{top}}\right\rfloor ⌊top⌋ 入堆。循环结束后,堆中所有元素之和就是答案。
class Solution {public long pickGifts(int[] gifts, int k) {var pq = new PriorityQueue<Integer>(gifts.length, (Integer a, Integer b) -> {return b- a;});for (int gift : gifts) pq.add(gift);for (int i = 0; i < k; ++i) {long m = pq.poll();pq.add((int) Math.sqrt(m)); // 留下平方根数量的礼物}long ans = 0;while (!pq.isEmpty()) ans += pq.poll();return ans;}
}
优化
- 如果堆顶等于 1 1 1 ,说明堆中所有元素都为 1 1 1 。由于 1 = 1 \sqrt{1} = 1 1=1 ,后续操作无法修改任何元素,可以直接退出循环。
- 原地堆化
heapify可以做到 O ( 1 ) \mathcal{O}(1) O(1) 的空间复杂度。部分语言用的标准库自带的堆化函数。
class Solution {
public:long long pickGifts(vector<int>& gifts, int k) {make_heap(gifts.begin(), gifts.end()); // 原地堆化,最大堆while (k-- && gifts[0] > 1) {pop_heap(gifts.begin(), gifts.end()); // 弹出堆顶并移到末尾gifts.back() = sqrt(gifts.back());push_heap(gifts.begin(), gifts.end()); // 把末尾元素入堆}return accumulate(gifts.begin(), gifts.end(), 0LL);}
};
复杂度分析:
- 时间复杂度: O ( n + k log n ) \mathcal{O}(n + k\log n) O(n+klogn) ,其中 n n n 为 gifts \textit{gifts} gifts 的长度。堆化需要 O ( n ) \mathcal{O}(n) O(n) 的时间(证明见下)。每次修改堆顶,需要 O ( log n ) \mathcal{O}(\log n) O(logn) 的时间。计算平方根有专门的 CPU 指令,可以视为 O ( 1 ) \mathcal{O}(1) O(1) 时间。所以总的时间复杂度为 O ( n + k log n ) \mathcal{O}(n + k\log n) O(n+klogn) 。
- 空间复杂度: O ( 1 ) \mathcal{O}(1) O(1) ,仅用到若干额外变量。
相关文章:

LeetCode 2558. 从数量最多的堆取走礼物【模拟,堆或原地堆化】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
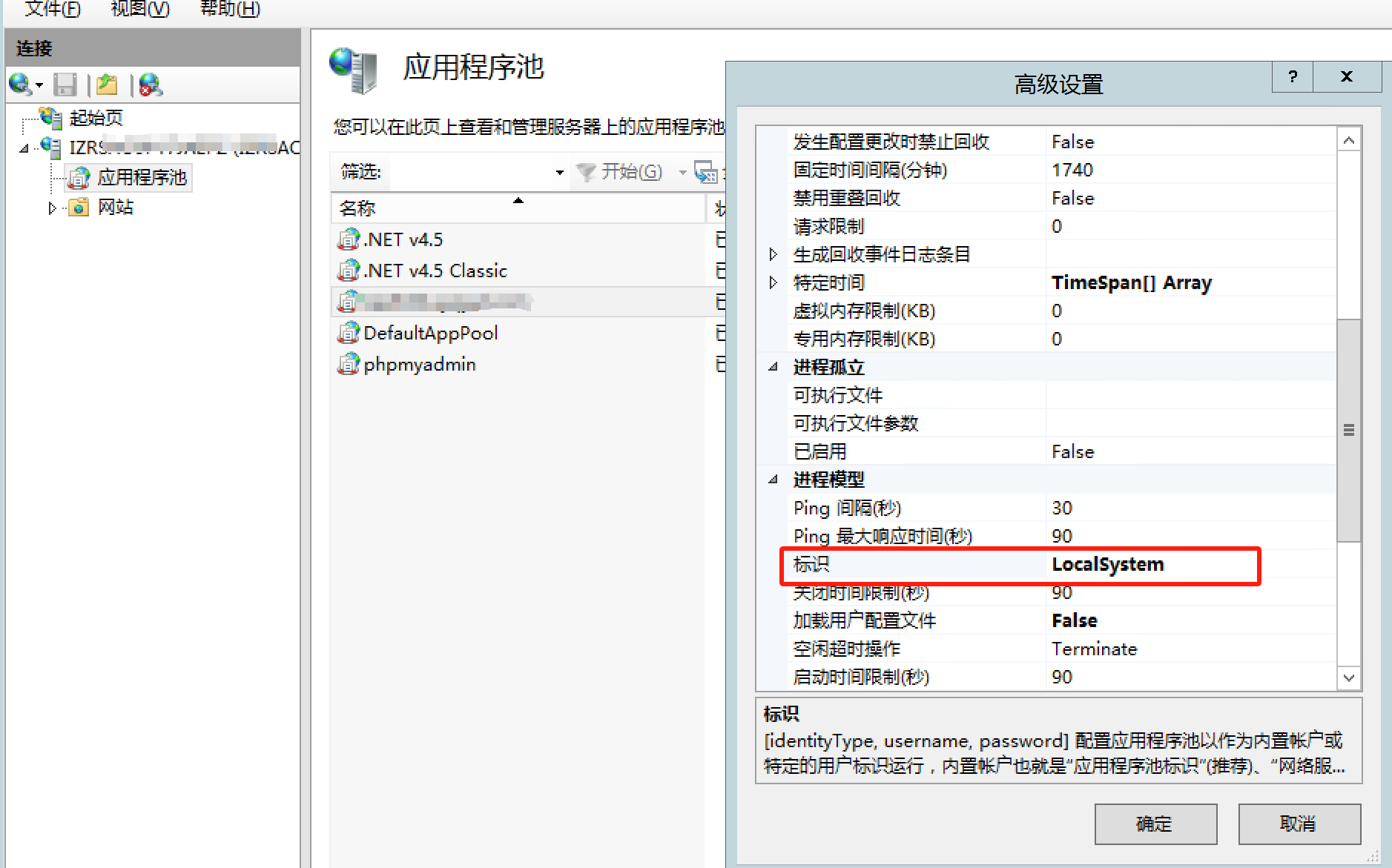
windows服务器环境下使用php调用com组件
Office设置 安装 office2013 且通过正版激活码激活 在组件服务 计算机 我的电脑 DOM 中找到 Microsoft Word 97 - 2003 文档 服务,右键属性 身份验证调整为 无 在 标识中 调整为 交互式用户 php环境设置 开启com组件扩展 在php.ini中设置 extensionphp_com_dotn…...

3DCAT+东风日产:共建线上个性化订车实时云渲染方案
近年来,随着5G网络和云计算技术的不断发展,交互式3D实时云看车正在成为一种新的看车方式。 与传统的到4S店实地考察不同,消费者可以足不出户,通过网络与终端设备即可实现全方位展示、自选汽车配色、模拟效果、快捷选车并进行个性…...

【VR开发】【Unity】【VRTK】1-无代码VRVR开发介绍
本篇开始精简讲解VRTK相关的知识。 VRTK是基于Unity的一套提供无代码VR开发的插件,这套插件开源,可商用,集合了目前可能的VR体验组件,可以让不会C#编程但想要开发VR体验的人在不写一行代码的前提下开发出心仪的VR作品。 这套组件问世后也很受欢迎,目前已经进化到了第四代…...
)
全国地级市最新城投债数据(2006-2023.2)
地级市-城投债数据是关于各地级市发行的城市投资建设项目资金债券的统计数据。这些数据对于研究者来说有着一定的参考价值。首先,地级市-城投债数据能够提供全国各地级市城投债发行的数量和规模情况,帮助研究者了解城市基础设施建设和经济发展的情况。其…...
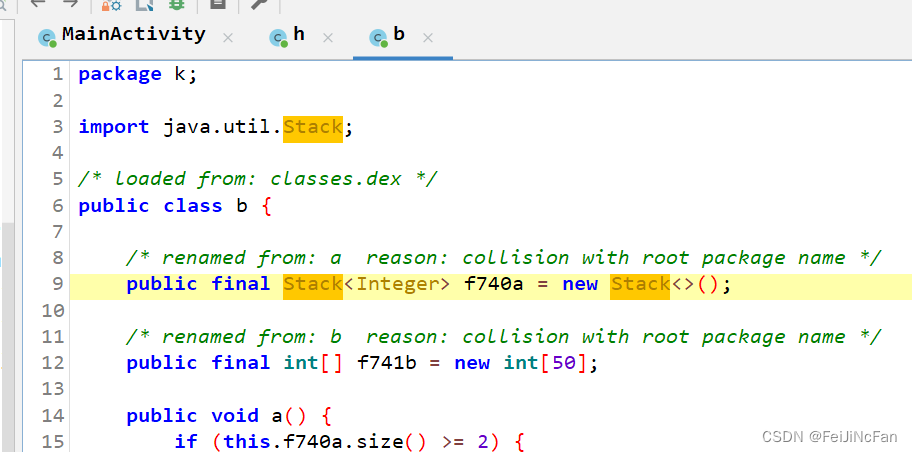
vm_flutter
附件地址 https://buuoj.cn/match/matches/195/challenges#vm_flutter 可以在buu下载到。 flutter我也不会,只是这个题目加密算法全部在java层,其实就是一个异或和相加。 反编译 package k;import java.util.Stack;/* loaded from: classes.dex */ pu…...
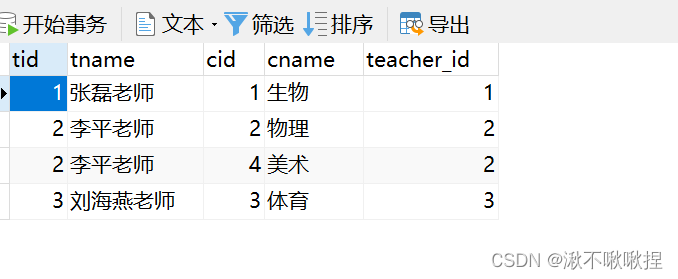
MySQL数据库#6
Python操作mysql 在使用Python连接mysql之前我们需要先下载一个第三方的模块 pymysql的模块,导入后再进行操作。 操作步骤:1. 先连接mysql host,port,charset,username password 库,等等。 import pymysql…...

YOLO v1(2016.5)
文章目录 AbstractIntroduction过去方法存在的问题我们提出的方法解决了... Unified DetectionNetwork DesignTrainingInference Comparison to Other Detection SystemsDeformable parts modelsR-CNNOther Fast DetectorsDeep MultiBoxOverFeatMultiGrasp ExperimentsConclusi…...

SQL比较两次的字段集合,找出并返回差异,主要用于更新记录事件
Create PROCEDURE [dbo].[SysGetTableFieldsCompare] -- Description: <比较两次的字段集合,找出并返回差异,主要用于更新记录事件> -- Return 0- 成功, -1- 没有这个表 -- Rev: 1.00 -- FieldsSource Nvarchar(max) , FieldsTarg…...

muduo源码剖析之Acceptor监听类
简介 Acceptor类用于创建套接字,设置套接字选项,调用socket()->bind()->listen()->accept()函数,接受连接,然后调用TcpServer设置的connect事件的回调。 listen()//在TcpServer::start中调用 封装了一个listen fd相关…...
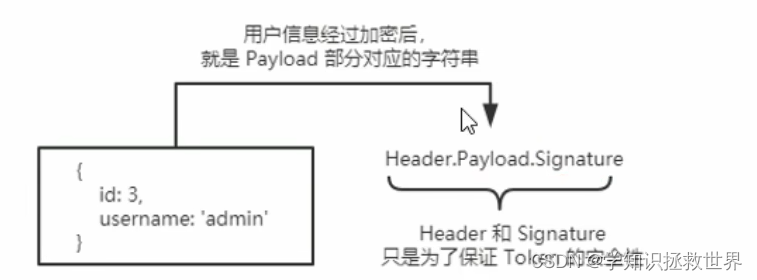
express session JWT JSON Web Token
了解 Session 认证的局限性 Session 认证机制需要配合 cookie 才能实现。由于 Cookie 默认不支持跨域访问,所以,当涉及到前端跨域请求后端接口的时候,需要做很多额外的配置,才能实现跨域 Session 认证。 注意: 当前端…...

负载均衡策略 LVS
一、集群功能分类 1、LB (1) 概念: LB:负载均衡 (Load Balancing) 是一种分发网络流量的技术,LB 负载均衡的基本原理是将传入的网络流量分发到多个后端服务器,以确保这些服务器都承担相似的工作负载,从而避免某一台…...
驱动开发6 IO多路复用——epoll
核心操作:一棵树、一张表、三个接口 相关案例 #include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <unistd.h> #include <stdlib.h> #include <string.h> #include <sys…...

【python学习笔记——列表】
1、列表定义 列表是写在方括号 [] 之间、用逗号分隔开的元素列表。 空列表 list[]非空列表 列表定义时例如list[‘csdn’, ‘is’ ,‘good’ ,2023],直接给列表内赋值 2、列表索引规则 列表名[start:stop:step],前闭后开,即取索引为start…...

TensorRT量化实战课YOLOv7量化:YOLOv7-PTQ量化(一)
目录 前言1. YOLOv7-PTQ量化流程2. 准备工作3. 插入QDQ节点3.1 自动插入QDQ节点3.2 手动插入QDQ节点 前言 手写 AI 推出的全新 TensorRT 模型量化实战课程,链接。记录下个人学习笔记,仅供自己参考。 该实战课程主要基于手写 AI 的 Latte 老师所出的 Tens…...

[微信小程序踩坑]微信小程序editor富文本组件渲染字符串时,内部图片超出大小导致无法正常渲染或回显(数据传输长度为 3458 KB,存在有性能问题!)
坑一:回显问题 富文本组件: <editor id"editor" name"{{name}}" style"font-size: 28rpx;color: #C9CDD4" read-only"{{true}}" placeholder"{{placeholder}}" bind:input"onChange11"…...
)
USACO12OPEN Balanced Cow Subsets G(meet in the middle)
洛谷P3067 [USACO12OPEN] Balanced Cow Subsets G 题目大意 我们定义一个奶牛集合 S S S是平衡的,当且仅当满足以下两个条件: S S S非空 S S S可以被划分为两个集合 A , B A,B A,B,满足 A A A里的奶牛产量之和等于 B B B里的牛奶产量之和 …...

GIT常用操作记录
1、后悔药:强制回退到某个具体历史提交记录,并强制推送到远程仓库 强制回退到某个具体历史提交记录,即要删除它之后的所有提交,可以用 git reset 命令。 首先找到目标提交记录的ID,可以在github远程仓库的历史提交记…...

【ETL工具】Datax-ETL-SqlServerToHDFS
🦄 个人主页——🎐个人主页 🎐✨🍁 🪁🍁🪁🍁🪁🍁🪁🍁 感谢点赞和关注 ,每天进步一点点!加油!&…...
概述)
Kubernetes (K8S)概述
1、K8S 是什么? K8S 的全称为 Kubernetes (K12345678S),PS:“嘛,写全称也太累了吧,不如整个缩写”。 1.1 作用 用于自动部署、扩展和管理“容器化(containerized)应用程序”的开源系统。 可以…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
