matlab simulink 直线一级倒立摆控制(自起摆和稳态控制)
1、内容简介
略
6-可以交流、咨询、答疑
2、内容说明
- 控制器设计
- 自起摆建模
规定正方向:顺时针为角度(力矩)正方向,向右为位移正方向。
在规定的正方向条件下,图 1 所示摆杆的角度φ为正值, 下车向右加速,故a为正值,则摆杆相对于小车的运动方程可表示为:
其中,J是指摆杆相对于摆杆转轴的转动惯量,
若垂直向下位置规定为π,则有:
由此可见,当正方向确定后,摆杆运动方程的形式与摆杆垂直向下位置的
规定角度无关。同理,假如开始时小车向左加速,摆杆向右摆起,,可得摆杆运动方程与上述相同。
-
- 自起摆算法设计与仿真
利用李雅谱诺夫原理构建控制律
由前面的分析可知,倒立摆摆杆的运动方程为:
,可改写成:
。
摆杆的能量可以由两部分构成:转动动能和势能,若将摆杆垂直向上位置的势能定义为零势能,则摆杆的能量Ep可表示为:
(1)
摆杆的目标位置是垂直向上,且摆起后的理想状态是,
均为0。由此可知,在摆起过程中,
(摆杆垂直向下位置),
(摆杆垂直向上位置),理想的控制率应保证
在摆起过程汇总始终是减小的。
小车在运动过程中的能量
, 由于在控制摆杆摆起到目标位置的同时,小车的横向位置应回到起摆时的位置,在构建小车的能量函数时应考虑小车的位移,为此,构建小车的广义能量函数为:
, 为了简
化后继的运算,与摆杆的能量函数之间能提取出公共项,引入一个比例系数r将
表达为:
。
构建一个李雅谱诺夫函数如下:
(2)
,其中
表示取
的符号。
为了确保
,取控制量
为如下形式:
(3)
其中α为权重系数,其值的选取是保证控制量
在许可的范围之内,保证系统尽可能快地收敛(达到目标值)。
当
时,除了在垂直向上位置,即倒立摆系统处于平衡位置
时,均有下式成立:
由此可知,当
取(3)所示的值时,系统在平衡位置是渐进稳定的,摆杆能摆起至垂直向上位置。
在实际运算中,当
时,系统将无法运算,为了防止该种情况发生,在实际控制时,可采用以下控制规律:
实际仿真中,取
。仿真步长设定为0.01s。

3、仿真分析
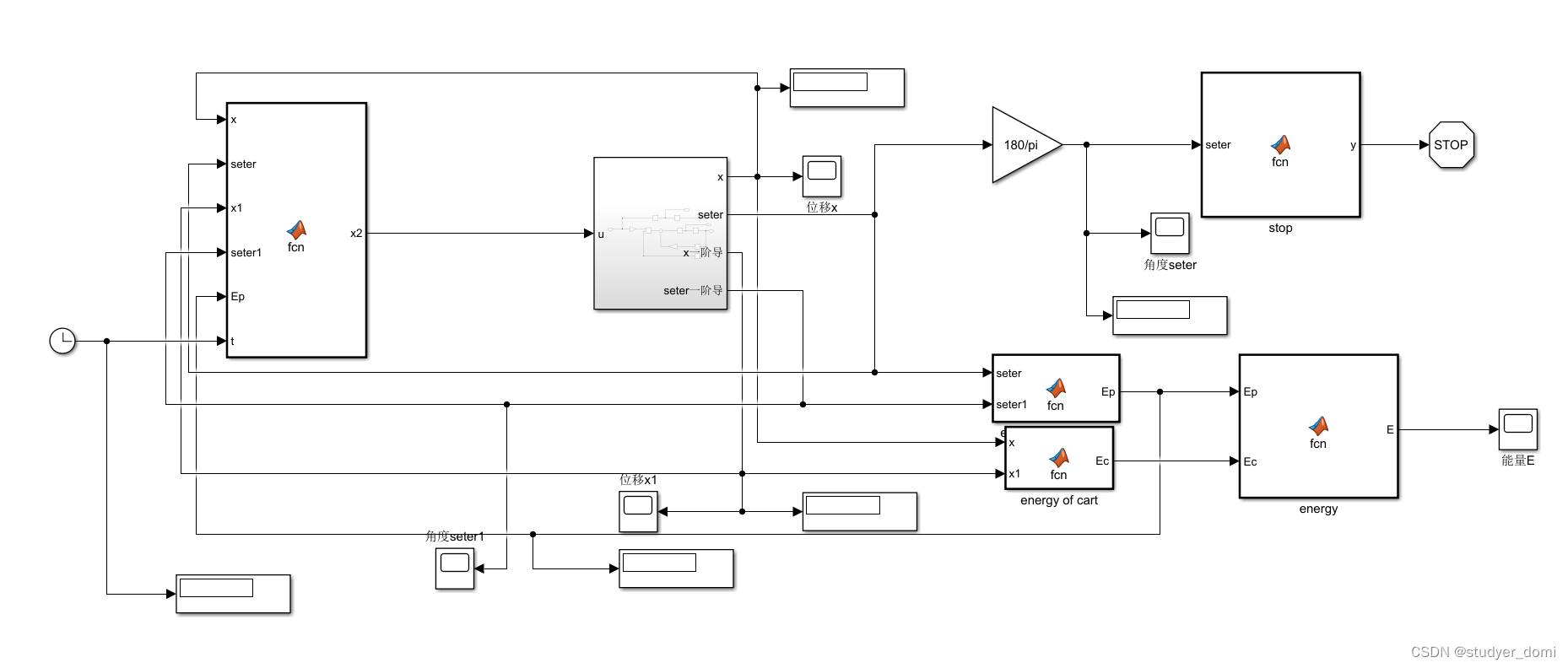
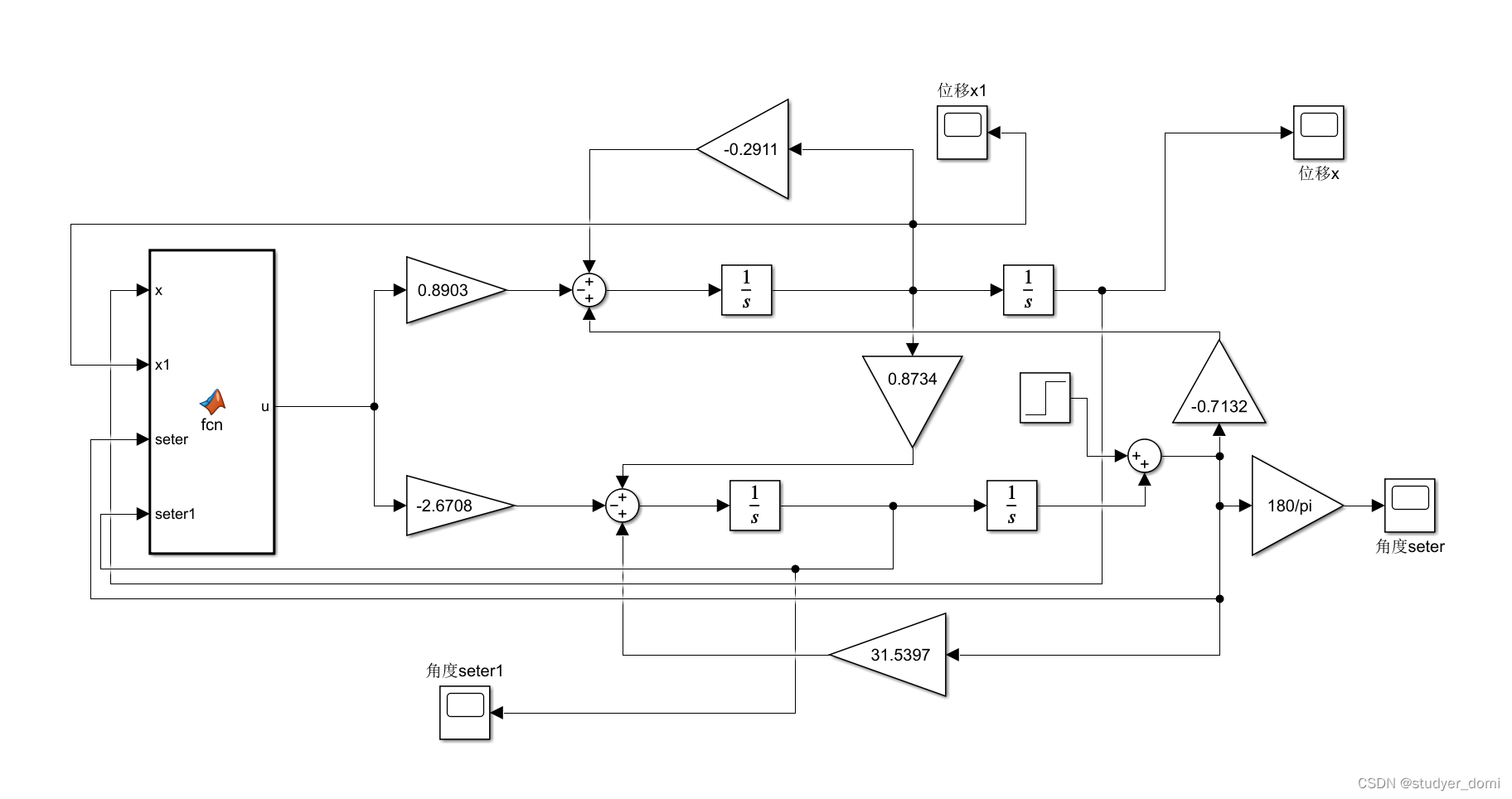
4、参考论文
略
相关文章:

matlab simulink 直线一级倒立摆控制(自起摆和稳态控制)
1、内容简介 略 6-可以交流、咨询、答疑 2、内容说明 控制器设计 自起摆建模 规定正方向:顺时针为角度(力矩)正方向,向右为位移正方向。 在规定的正方向条件下,图 1 所示摆杆的角度φ为正值, 下车向右加…...

Transformers实战(二)快速入门文本相似度、检索式对话机器人
Transformers实战(二)快速入门文本相似度、检索式对话机器人 1、文本相似度 1.1 文本相似度简介 文本匹配是一个较为宽泛的概念,基本上只要涉及到两段文本之间关系的,都可以被看作是一种文本匹配的任务, 只是在具体…...
【错误解决方案】ModuleNotFoundError: No module named ‘PeptideBuilder‘
1. 错误提示 在python程序中,试图导入一个不存在的模块PeptideBuilder导致的错误: 错误提示:ModuleNotFoundError: No module named PeptideBuilder 2. 解决方案 解决方案是确保你已经正确安装了PeptideBuilder模块。你可以通过pip来安装它…...

汇编学习(1)
汇编、CPU架构、指令集、硬编码之间的关系 ● 汇编语言:这是一种低级语言,用于与硬件直接交互。它是由人类可读的机器码或指令组成的,这些指令告诉CPU如何执行特定的任务。每条汇编指令都有一个对应的机器码指令,CPU可以理解和执…...

C#,数值计算——分类与推理Svmlinkernel的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { public class Svmlinkernel : Svmgenkernel { public int n { get; set; } public double[] mu { get; set; } public Svmlinkernel(double[,] ddata, double[] yy) : base(yy, ddata) …...
【鸿蒙软件开发】ArkTS容器组件之Badge
文章目录 前言一、Badge组件1.1 子组件1.2 接口接口1参数 接口2参数 BadgePosition枚举说明BadgeStyle对象说明 1.3 示例代码 总结 前言 Badge组件:可以附加在单个组件上用于信息标记的容器组件。 一、Badge组件 可以附加在单个组件上用于信息标记的容器组件。 说…...
H5游戏源码分享-命悬一线
H5游戏源码分享-命悬一线 在合适的时机跳下绳子,能安全站到木桩上,就通过。 游戏源码 <!DOCTYPE html> <html> <head><meta http-equiv"Content-Type" content"text/html; charsetutf-8" /><meta name&…...

【电路笔记】-交流电阻和阻抗
交流电阻和阻抗 文章目录 交流电阻和阻抗1、概述:电阻率2、交流状态与直流状态近似性3、交流状态与直流状态的差异性3.1 趋肤效应(The Skin Effect)3.2 靠近效应(The Proximity Effect) 4、总结 电阻是一种特性,用于表征当电压差施…...
android开发使用OkHttp自带的WebSocket实现IM功能
一、背景 android app开发经常会有IM需求,很多新手不晓得如何入手,难点在于通讯不中断。其实android发展到今天,很多技术都很完善,有很多类似框架可以实现。例如有:okhttp自带的websocket框架、easysocket等等。本文主…...

前端小技巧: TS实现柯里化函数
实现 curry 函数,把其他函数柯里化 curry 返回一个函数fn执行fn, 中间状态返回函数,如 add(1), 或者 add(1)(2)最后返回执行结果,如 add(1)(2)(3) function curry(fn:Function) {const fnArgsLen fn.length // 传入函数的参数长度let args…...

【算法-数组2】有序数组的平方 和 长度最小的子数组
今天,带来数组相关算法的讲解。文中不足错漏之处望请斧正! 理论基础点这里 有序数组的平方 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输…...

H5游戏源码分享-接苹果游戏拼手速
H5游戏源码分享-接苹果游戏拼手速 看看在20秒内能接多少个苹果 <html> <head><title>我是你的小苹果</title><meta charset"utf-8"/><meta name"viewport" content"initial-scale1, user-scalableno, minimum-scale…...
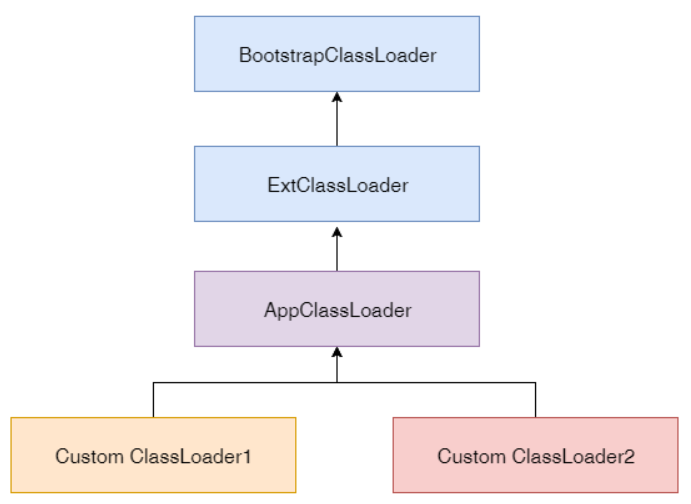
详解类生到死的来龙去脉
类生命周期和加载过程 一个类在 JVM 里的生命周期有 7 个阶段,分别是加载(Loading)、校验(Verification)、准备(Preparation)、解析(Resolution)、初始化(Ini…...
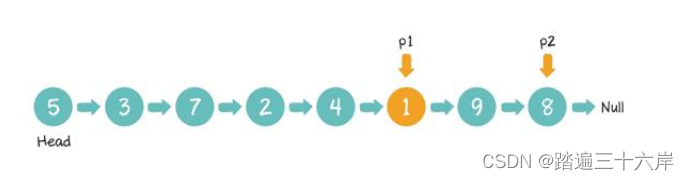
寻找倒数第K个节点
这篇文章也是凑数的 ... 寻找倒数第K个节点 描述 : 找出单向链表中倒数第 k 个节点。返回该节点的值。 题目 : LeetCode 返回倒数第K个节点 : 面试题 02.02. 返回倒数第 k 个节点 说明 : 给定的 k 保证是有效的。 分析 : 我们给出个例子 : 首先,我们创建两个…...
)
[ROS系列]ubuntu 20.04 从零配置orbslam3(无坑版)
目录 背景: 结果展示: 一、配置虚拟机 二、 同步网络时间 三、ping网络 四、 安装ros 五、下载源码 六、下载orb_slam3 error1:Pangolin error2: ./HelloPangolin: error while loading shared libraries: libpango_windowing.so: cannot open shared object file…...

网络协议--TCP的保活定时器
23.1 引言 许多TCP/IP的初学者会很惊奇地发现可以没有任何数据流通过一个空闲的TCP连接。也就是说,如果TCP连接的双方都没有向对方发送数据,则在两个TCP模块之间不交换任何信息。例如,没有可以在其他网络协议中发现的轮询。这意味着我们可以…...
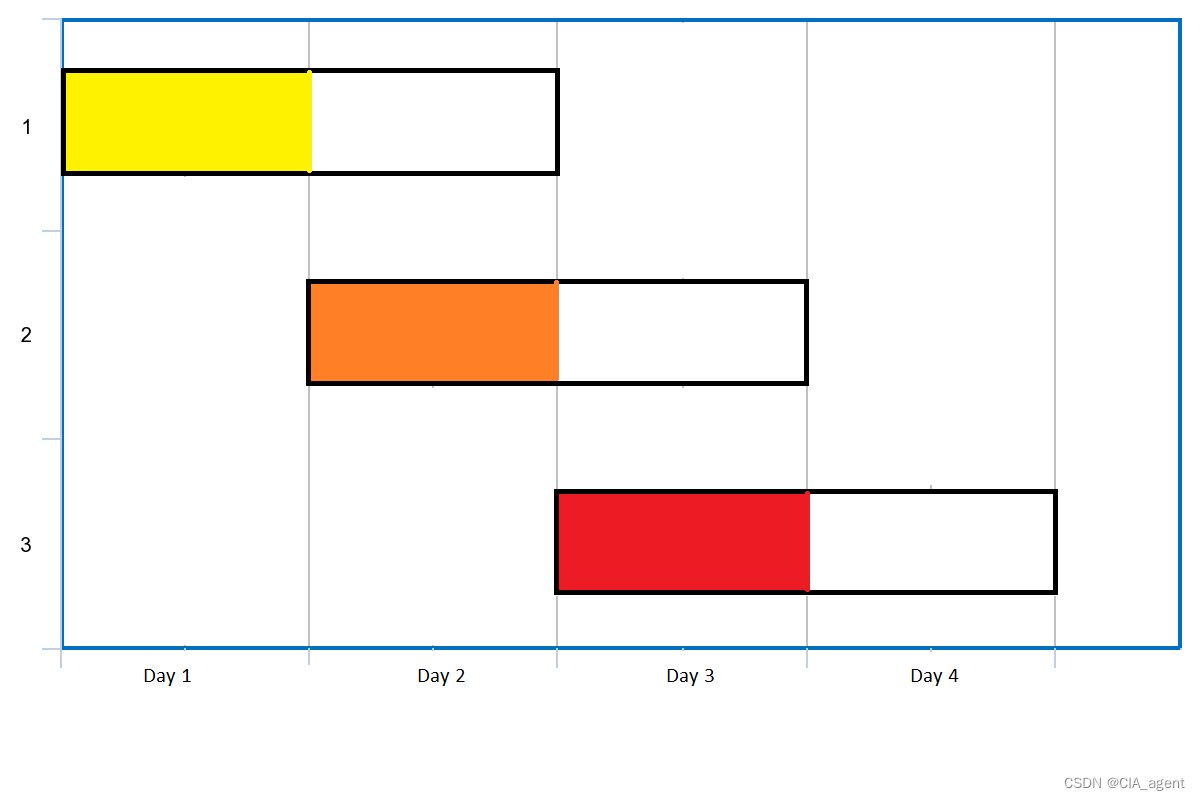
leetcode 1353. 最多可以参加的会议数目
给你一个数组 events,其中 events[i] [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。 你可以在满足 startDayi < d < endDayi 中的任意一天 d 参加会议 i 。注意,一天只能参加一个会议。 请你返回…...
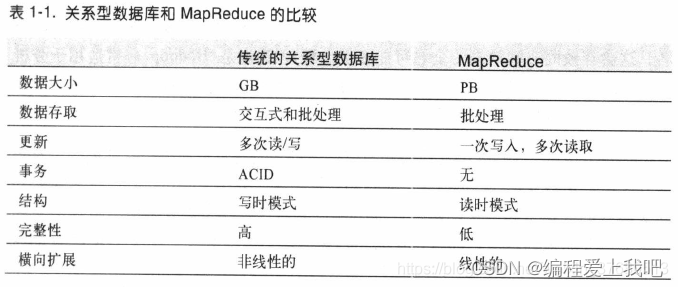
hadoop权威指南第四版
第一部分 HaDOOP基础知识 1.1 面临的问题 存储越来越大,读写跟不上。 并行读多个磁盘。 问题1 磁盘损坏 – 备份数据HDFS 问题2 读取多个磁盘用于分析,数据容易出错 --MR 编程模型 1.2 衍生品 1 在线访问的组件是hbase 。一种使用hdfs底层存储的模型。…...

LeetCode75——Day20
文章目录 一、题目二、题解 一、题目 2215. Find the Difference of Two Arrays Given two 0-indexed integer arrays nums1 and nums2, return a list answer of size 2 where: answer[0] is a list of all distinct integers in nums1 which are not present in nums2. an…...

搭建微信小程序环境及项目结构介绍
一、注册 访问微信公众平台,将鼠标的光标置于账号分类中的小程序上, 点击‘查看详情’ 点击“前往注册” 下方也可以点击注册: 小程序注册页面: 步骤a:进入小程序注册页,根据指引填写信息和提交相应的资料&#x…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
