【机器学习】朴素贝叶斯算法基本原理与计算案例
朴素贝叶斯算法基本原理与计算案例
文章目录
- 朴素贝叶斯算法基本原理与计算案例
- 1. 朴素贝叶斯算法的基本原理
- 2. 概率基础
- 3. 朴素贝叶斯简单计算案例
- 4. 朴素贝叶斯算法对文本进行分类
- 5. 拉普拉斯平滑系数
- 6. 案例:20类新闻分类
- 7. 总结
1. 朴素贝叶斯算法的基本原理
朴素贝叶斯算法的基本原理建立在贝叶斯定理的基础上,它用于分类和概率估计。算法的核心思想是根据已知数据,计算不同类别的条件概率,并利用这些概率进行分类。以下是朴素贝叶斯算法的基本原理:
-
贝叶斯定理:朴素贝叶斯算法基于贝叶斯定理,该定理描述了在给定某些观察数据的情况下,如何计算某一事件的条件概率。数学表示如下:
P(A|B) = (P(B|A) * P(A)) / P(B)
- P(A|B):在给定B的条件下,事件A发生的概率。
- P(B|A):在给定A的条件下,事件B发生的概率。
- P(A):事件A发生的先验概率。
- P(B):事件B发生的先验概率。
-
朴素假设:朴素贝叶斯算法做出一个朴素的假设,即特征之间是相互独立的。这意味着在分类时,它假设每个特征对于类别的影响是相互独立的。尽管这个假设在实际情况中通常不成立,但它简化了计算,使算法易于实现。
-
学习阶段:在朴素贝叶斯的学习阶段,使用已知的训练数据来估计每个特征在不同类别下的条件概率。这包括计算每个类别的先验概率(每个类别发生的概率)以及每个特征在每个类别下的条件概率。
-
预测阶段:在预测阶段,算法使用已经估计的条件概率来对新的、未知的数据点进行分类。它计算每个类别的后验概率(给定数据点的情况下,每个类别发生的概率),然后选择具有最高后验概率的类别作为预测结果。
具体步骤包括计算每个特征在给定类别下的条件概率,然后将这些条件概率组合起来,使用贝叶斯定理来计算后验概率。
朴素贝叶斯算法在特征之间相关性较高的情况下可能表现不佳,因为它的独立性假设通常不成立。
2. 概率基础
- 联合概率:包含多个条件,且这些条件同时成立的概率记作:P(A,B,…)
- 条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率,记作P(A|B)
- 相互独立:如果P(A,B)=P(A)*P(B),则称事件A和事件B相互独立
3. 朴素贝叶斯简单计算案例
- 下面是训练集:
| 样本数 | 职业 | 体型 | 女神是否喜欢 |
|---|---|---|---|
| 1 | 程序员 | 超重 | 不喜欢 |
| 2 | 产品经理 | 匀称 | 喜欢 |
| 3 | 程序员 | 匀称 | 喜欢 |
| 4 | 程序员 | 超重 | 喜欢 |
| 5 | 美工 | 匀称 | 不喜欢 |
| 6 | 美工 | 超重 | 不喜欢 |
| 7 | 产品经理 | 匀称 | 喜欢 |
- 下面是测试集:
| 测试集 | 小明 | 产品经理 | 超重 | ??? |
|---|
我们先来明确一下目标,已知小明是一个产品经理,体重超重,是否会被女神喜欢,从测试集来看,这是一个分类问题,而且还是一个二分类问题。先来解决以下的概率问题:
- 女神喜欢的概率?P(喜欢)=4/7
- 职业是程序员并且体型匀称的概率?P(程序员,匀称)=1/7 联合概率
- 在女神喜欢的条件下,职业是程序员的概率?P(程序|喜欢)=2/4=1/2 条件概率
- 在女神喜欢的条件下,职业是程序员,体重是超重的概率?P(程序员,超重|喜欢)=1/4 联合条件概率
解决完以上的问题之后,就来解决小明的问题。
- 目标:P(喜欢|产品经理,超重)=? and 贝叶斯公式
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
- 接下来就是简单的计算,在计算的过程中,我们会发现,P(产品经理,超重)=0,回到朴素贝叶斯算法的i定义,两事件之间是相互独立的,所以P(产品经理,超重)=P(产品经理)*P(超重)=7/12,所以很大可能内女神喜欢,但是也是不实际的,因为样本量太小,而且做出了相互独立的假设。
4. 朴素贝叶斯算法对文本进行分类
| 文档ID | 文档中的词 | 属于c=China类 | |
|---|---|---|---|
| 训练集 | 1 | Chinese Beijing Chinese | Yes |
| 2 | Chinese Chinese Shanghai | Yes | |
| 3 | Chinese Macao | Yes | |
| 4 | Tokyo Japan Chinese | No | |
| 测试集 | 5 | Chinese Chinese Chinese Tokyo Japan | ? |
如果朴素贝叶斯公式用在文章分类的场景中,我们可以这样看:
P ( C ∣ F 1 , F 2 , F 3 , F 4... ) = P ( F 1 , F 2 , F 3 , F 4... ∣ C ) ⋅ P ( C ) P ( F 1 , F 2 , F 3 , F 4... ) P(C|F1,F2,F3,F4...) = \frac{P(F1,F2,F3,F4...|C) \cdot P(C)}{P(F1,F2,F3,F4...)} P(C∣F1,F2,F3,F4...)=P(F1,F2,F3,F4...)P(F1,F2,F3,F4...∣C)⋅P(C)
其中C可以是不同类别,公式分为三个部分:
- P©:每个文档类别的概率(某文档类别数/总文档数量)
- P(W|C):给定类别下特征(被预测文档中出现的词)的概率,计算方法:P(F1|C)=Ni/N(训练文档中去计算,Ni为该F1词在C类别所有文档中出现的次数,N为所需类别C下的文档所有词出现次数和)
- P(F1,F2,F3,…):预测文档中每个词的概率
首先明确目标,我们要求的是P(C|Chinese,Chinese,Chinese,Tokyo,Japan),即求:P(Chinese,Chinese,Chinese,Tokyo,Japan|C),P©,P(Chinese,Chinese,Chinese,Tokyo,Japan)
- 根据朴素贝叶斯算法,假设每一个事件相互独立所以:P(Chinese,Chinese,Chinese,Tokyo,Japan|C)=P(Chinese|C)^3*P(Tokyo|C)*P(Japan|C),我们可以算出P(Chinese|C)=5/8,而在算P(Tokyo|C)和P(Japan|C)的时候发现为0,这会对结果产生很大的影响,发生这种情况的原因就是样本量太小了,那么如何避免这情况呢?这就要用到拉普拉斯平滑系数了。
5. 拉普拉斯平滑系数
拉普拉斯平滑系数是一种在统计学和机器学习中用于处理概率估计问题的技术。它的主要作用是解决在统计分析中遇到的一些问题,如零概率问题和过拟合问题。具体来说,拉普拉斯平滑系数通常用于计算一个特定事件在一个样本空间中的概率。在统计中,如果一个事件在训练数据中没有观察到,那么根据最大似然估计,其概率会被估计为零。这可能导致问题,因为零概率的事件在实际应用中可能不是完全不可能发生的,而只是未观察到而已。
简单来说,就是防止计算出的分类概率为0
P ( F 1 ∣ C ) = N i + α N + α m P(F1|C) = \frac{Ni+α}{N+αm} P(F1∣C)=N+αmNi+α
α为指定系数一般为1,m为训练文档中统计出的特征词个数,例如:
P(Chinese|C)=(5+1)/(8+1*6)=3/7
P(Tokyo|C)=(0+1)/(8+1*6)=1/14
P(Japean|C)=(0+1)/(8+1*6)=1/14
6. 案例:20类新闻分类
- sklearn.naive_bayes.MultinomialNB(alpha=1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_splitdef nb_news_demo():"""用朴素贝叶斯算法对新闻进行分类1.获取数据2.划分数据集3.特征工程,文本特征抽取-tfidf4.朴素贝叶斯算法预估器5.模型评估:return:"""news = fetch_20newsgroups(subset= "all")x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)transfer = TfidfVectorizer()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)estimator = MultinomialNB()estimator.fit(x_train, y_train)# 模型评估,方法1:直接比对真实值和预测值y_predict = estimator.predict(x_test)print("y_predict:\n", y_predict)print("直接比对真实值和预测值:\n", y_test == y_predict)# 方法2:计算准确率score = estimator.score(x_test, y_test)print("准确率为:", score)return None
y_predict:[ 4 15 9 ... 4 0 6]
直接比对真实值和预测值:[ True False True ... False False True]
准确率为: 0.8499575551782682
7. 总结
- 优点:朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率;对缺失数据不太敏感,算法比较简单,常用于文本分类;分类准确率高,速度快。
- 缺点:由于使用了样本属性独立性的假设,所以如果特征属性有关联时效果不好。
相关文章:

【机器学习】朴素贝叶斯算法基本原理与计算案例
朴素贝叶斯算法基本原理与计算案例 文章目录 朴素贝叶斯算法基本原理与计算案例1. 朴素贝叶斯算法的基本原理2. 概率基础3. 朴素贝叶斯简单计算案例4. 朴素贝叶斯算法对文本进行分类5. 拉普拉斯平滑系数6. 案例:20类新闻分类7. 总结 1. 朴素贝叶斯算法的基本原理 朴…...

redis6.0源码分析:简单动态字符串sds
文章目录 sds简介与特性(面试)sds结构模型数据结构苛刻的数据优化数据结构优化uintX_t对齐填充 sds优势O(1)时间复杂度获取字符串长度二进制安全杜绝缓冲区溢出自动扩容机制——sdsMakeRoomFor方法 内存重分配次数优化 sds最长是多少部分API源码解读创建sds释放sds sds简介与特…...

1.7 攻击面和攻击树
思维导图: 1.7 攻击面与攻击树 攻击面: 描述计算机和网络系统面对的安全威胁和攻击。 定义: 攻击面是由系统中可访问和可利用的漏洞所组成。常见攻击面: 向外部Web及其他服务器开放的端口和相应代码。防火墙内部的服务。处理入站数据、电子邮件、XML文件、Office文档…...

解决input在谷歌浏览器自动填充问题
解决input在谷歌浏览器自动填充问题 <input typepassword readonly onfocus"this.removeAttribute(readonly);" />...
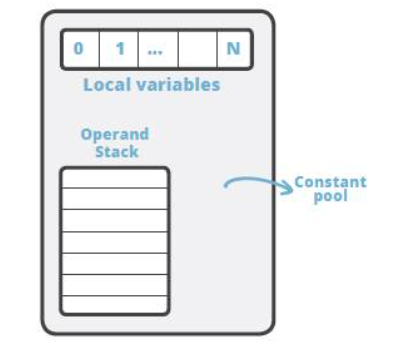
Java字节码技术
Java 字节码简介 Java 中的字节码,英文名为 bytecode, 是 Java 代码编译后的中间代码格式。JVM 需要读取并解析字节码才能执行相应的任务。 从技术人员的角度看,Java 字节码是 JVM 的指令集。JVM 加载字节码格式的 class 文件,校验之后通过 J…...
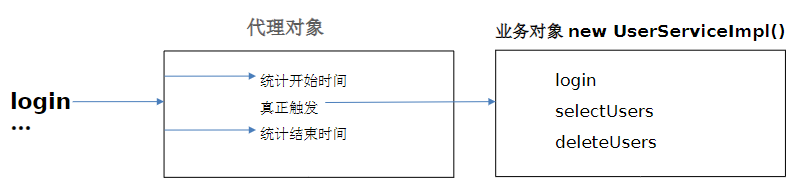
Java SE 学习笔记(十八)—— 注解、动态代理
目录 1 注解1.1 注解概述1.2 自定义注解1.3 元注解1.4 注解解析1.5 注解应用于 junit 框架 2 动态代理2.1 问题引入2.2 动态代理实现 1 注解 1.1 注解概述 Java 注解(Annotation)又称Java标注,是JDK 5.0引入的一种注释机制,Java语…...

虚拟内存之请求分页管理
一、与基本分页存储管理的区别 程序执行过程中,访问信息不在内存时,OS需要从外存调入内存。——>调页功能 内存空间不够时,OS需要将内存中暂时用不到的信息换出到外存。——>页面置换功能 二、页表机制 1.页表:需要知道页面…...

lazarus开发:提升sqlite数据插入速度
目录 1 前言 2 优化数据容器 3 开启事务插入数据 4 其他方面优化 1 前言 近期有一个需求是向数据库中插入excel文件中的10万多条数据,接近70个字段。最初整个插入数据时间是大约40分钟,经过优化调整后,大幅优化为大约5分钟。这里简单介绍…...
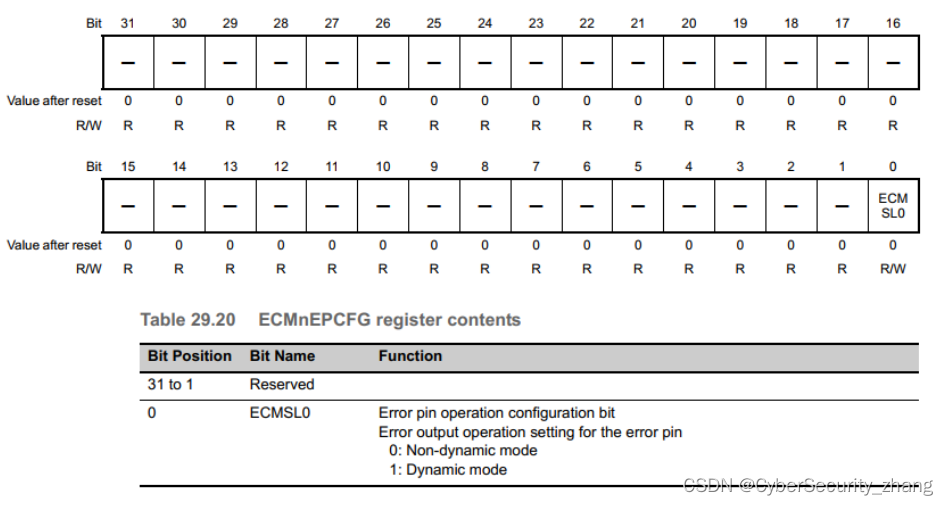
瑞萨RH850-P1X ECM和英飞凌TC3xx SMU对比
1.1 基本结构 P1X ECM(Error Control Module)收集从不同的错误源和监控电路发来的错误信号,并通过error pin(ERROROUTZ)对外输出、产生中断并发出ECM reset信号。 P1x-C系列根据产品型号不同,ECM个数也不相同,如下: 对应寄存器基地…...
Ajax学习笔记第三天
做决定之前仔细考虑,一旦作了决定就要勇往直前、坚持到底! 【1 ikunGG邮箱注册】 整个流程展示: 1.文件目录 2.页面效果展示及代码 mysql数据库中的初始表 2.1 主页 09.html:里面代码部分解释 display: inline-block; 让块元素h1变成行内…...

ESP32-C3 低功耗懒人开关:传统开关轻松上云和本地控制
项目背景 随着科技的快速发展,智能家居已经成为我们日常生活的一部分。而对于基础设施已经配备完毕的家庭而言,对家居设备的智能化改造是一项相对困难的工作。本文将分享一款基于 Wi-Fi 的低功耗懒人开关—— “ESP32-C3 管灯熊猫”。将智能的 “ESP32-…...

前端学习路线指南:从入门到精通【①】
前言 作为一个前端开发者,学习前端技术是必不可少的。然而,由于前端领域的广阔和不断演进的技术栈,对于初学者来说可能会感到困惑。本篇文章将为你提供一个清晰的前端学习路线,帮助你系统地掌握前端开发技能,并成为一名…...

Flash模拟EEPROM原理浅析
根据ST的手册,我们可以看到,外挂EEPROM和Dflash模拟EEPROM,区别如下: 很明显,模拟EEprom的写入速度要远远快于外挂eeprom(有数据传输机制); 其次,外挂EEPROM不需要擦除即可实现写入数据…...
Typora 最新激活方法
Markdown是一种可以使用普通文本编辑器编写的标记语言,通过简单的标记语法,它可以使普通文本内容具有一定的格式,其目标是实现易读易写。而Typora则是一个非常不错的Markdown编辑器,它的界面非常的简洁直观,并且功能各…...
jenkins如何安装?
docker pull jenkins/jenkins:lts-centos7-jdk8 2.docker-compose.yml version: 3 services:jenkins:image: jenkins/jenkins:lts-centos7-jdk8container_name: my-jenkinsports:- "8080:8080" # 映射 Jenkins Web 界面端口volumes:- jenkins_home:/var/jenkins_h…...

从零开始的LINUX(三)
bc:进行浮点数运算 uname:查看当前的操作系统 ctrlc:中止当前正在执行的程序 ctrld:退出xshell shutdown:关机 reboot:重启 shell外壳: 作用:1、命令解释(将输入的程序…...
CleanMyMac2024永久免费版Mac系统磁盘清理工具
Cleanmymac对很多用户来说已经非常熟悉了,因为在网上如果你搜寻有关清理mac系统方面的软件时,占比非常多的会是cleanmymac的相关消息。许多刚从Windows系统转向Mac系统怀抱的用户,一开始难免不习惯,因为Mac系统没有像Windows一样的…...

HashSet 元素不重复
HashSet通过底层使用HashMap来保证元素不重复。具体来说,HashSet内部维护一个HashMap,其中元素存储在HashMap的key上,而所有的value都指向同一个共享的内部对象。在存储元素时,HashSet会根据元素的hashCode值来确定其在HashMap中的…...
基于SpringBoot的二手车交易系统的设计与实现
目录 前言 一、技术栈 二、系统功能介绍 管理员功能实现 商家管理 公告信息管理 论坛管理 商家功能实现 汽车管理 汽车留言管理 论坛管理 用户功能实现 汽车信息 在线论坛 公告信息 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 如今社会上各行…...
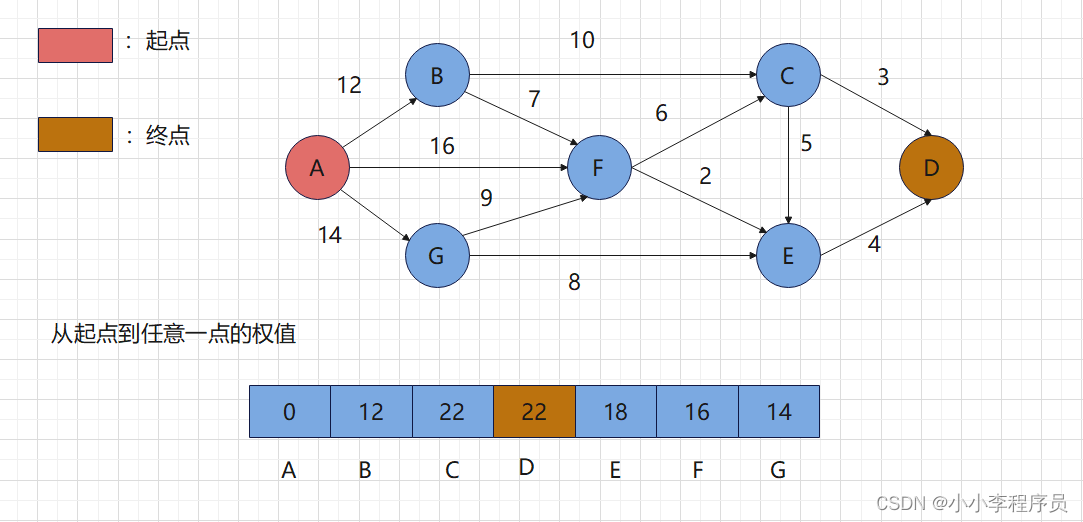
最短路径:迪杰斯特拉算法
简介 英文名Dijkstra 作用:找到路中指定起点到指定终点的带权最短路径 核心步骤 1)确定起点,终点 2)从未走过的点中选取从起点到权值最小点作为中心点 3)如果满足 起点到中心点权值 中心点到指定其他点的权值 < 起…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
