信号类型(雷达)——脉冲雷达(三)
系列文章目录
《信号类型(雷达+通信)》
《信号类型(雷达)——雷达波形认识(一)》
《信号类型(雷达)——连续波雷达(二)》
文章目录
前言
一、相参雷达
1.1 固定频脉冲信号
1.2 线性调频脉冲信号
1.3 捷变频雷达信号
1.4 伪随机相位编码信号
二、线性调频雷达的相参与非相参
总结
前言
连续被雷达在工作过程中,发射信号泄漏会对接收机造成干扰,情况主要有两种:一种是大信号干扰使得接收机压缩增益或出现饱和,甚至造成接收机阻塞,通常可以通过将收发天线进行物理隔离来解决;另一种是发射信号的边带噪声将微弱的回波信号淹没,对接收机的目标检测造成影响。而脉冲雷达因为发射波形有一定的占空比,因此信号发射以及回波接收过程可以在时间上实现分离,这就可以避免连续波雷达中发射信号泄露的问题。
脉冲雷达中相参与非相参体制主要由硬件实现水平决定, 一般相参体制雷达所需硬件要求高,成本比较高,本节主要结合简单的仿真介绍常见的脉冲雷达信号,并且通过对比说明脉冲雷达相参的重要性。
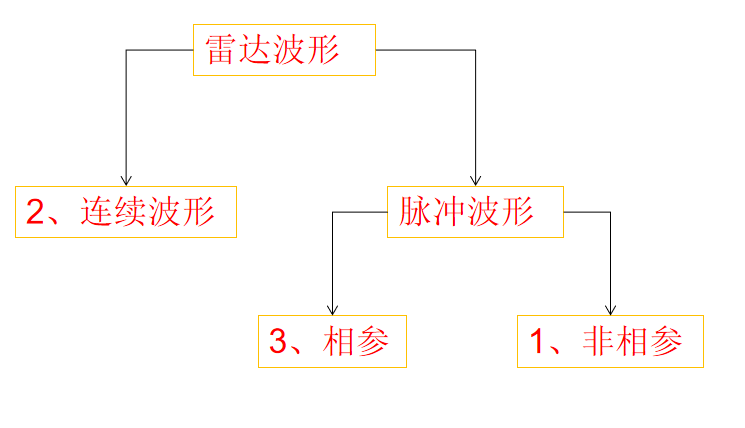
一、脉冲相参雷达
脉冲波形主要有四个基本特征:载频(就是雷达发射机产生大功率电磁波信号在未受调制前的频率)、脉冲宽度(脉冲的持续时间)、脉冲重复频率(每秒钟发射脉冲的个数)、脉冲调制参数(载波相位或频率调制参数)。固定频脉冲信号主要涉及前3个特征;线性调频脉冲信号是对载波的频率进行线性调制,因此在存在调频率的脉冲调制参数,其与脉宽共同决定脉冲信号带宽;捷变频雷达与线性调频率雷达主要区别在于捷变频雷达每个载频中心是随机捷变的,而一般的线性调频脉冲雷达载频中心是固定的;伪随机相位编码雷达的对载波相位进行伪随机编码,增加脉冲信号带宽,进而提高距离分辨率。本节主要围绕多目标分辨对不同体制的雷达进行分析:
1.1 固定频脉冲信号
波形特点:一系列载频固定的脉冲串信号,脉冲波形具有一定的占空比,发射波形为:
则接收信号波形为:
其中
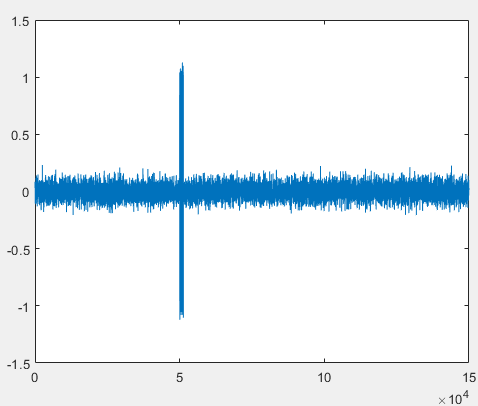
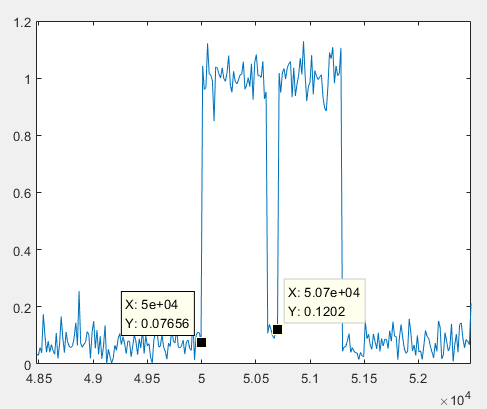
仿真时,考虑某个脉冲的多目标分辨性能。中心载频3GHz,脉冲重复间隔1ms,脉宽4us,目标1距离50km,目标2距离50km+0.7km。脉冲回波信号如下所示,右图为左图脉冲回波的放大图,可以看出距离分辨率由脉宽决定,约为
1.2 线性调频脉冲信号
波形特点:一系列调频率参数相同的线性调频脉冲串信号,脉冲波形具有一定的占空比,发射波形为:
则接收信号波形为:
其中
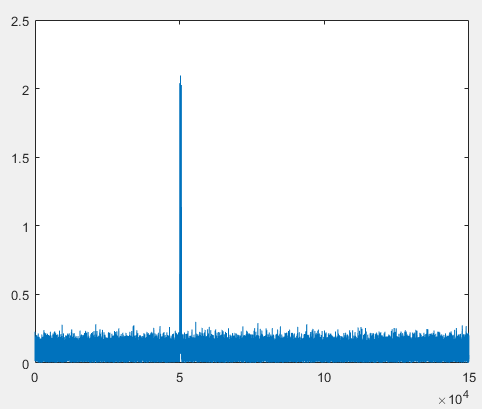
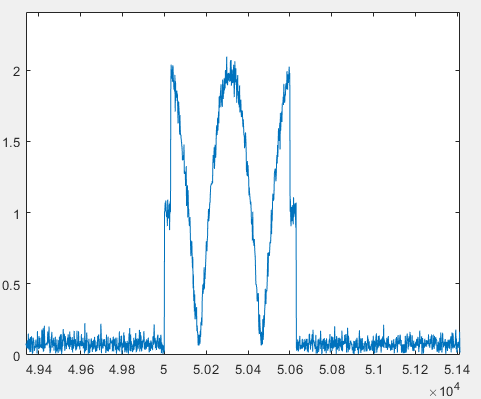
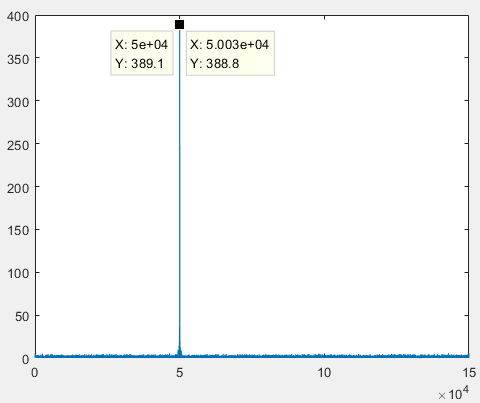
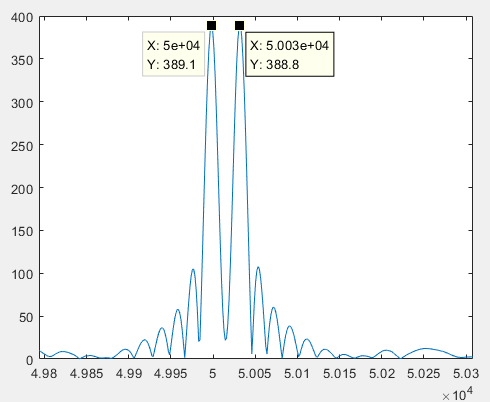
仿真时,考虑某个脉冲的多目标分辨性能。中心载频3GHz,脉冲重复间隔1ms,脉宽4us,调频率2.5e12 Hz/s,目标1距离50km,目标2距离50km+30m。脉冲回波信号如上图所示,右图为左图脉冲回波的放大图,此时目标分辨不出来。下图是经过脉冲压缩后的结果,目标能够分辨,并且距离分辨率由脉冲带宽决定,约为
1.3 捷变频雷达信号
波形特点:一系列调频率参数相同载频变化的线性调频脉冲串信号,脉冲波形具有一定的占空比,发射波形为:
其中为捷变载频,则接收信号波形为
其中
针对单个脉冲的分析,捷变频雷达与固定频的线性调频雷达没有太大区别,这里不再赘述。
1.4 伪随机相位编码信号
波形特点:一系列相位伪随机变化的脉冲串信号,脉冲波形具有一定的占空比,发射波形为:
其中为随机相位,则接收信号波形为
其中
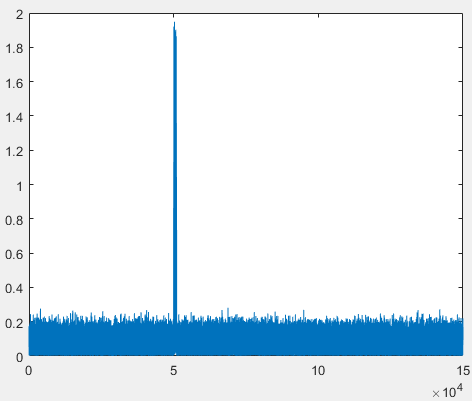
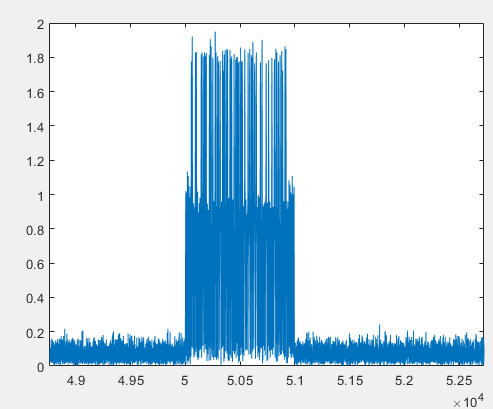
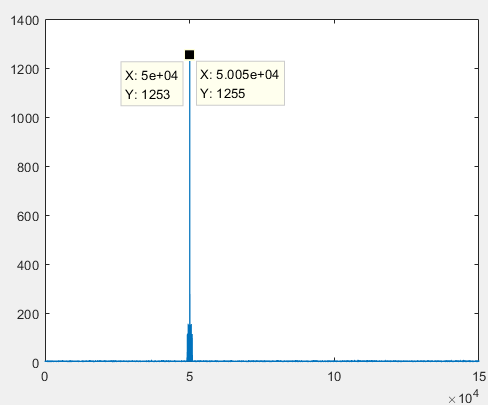
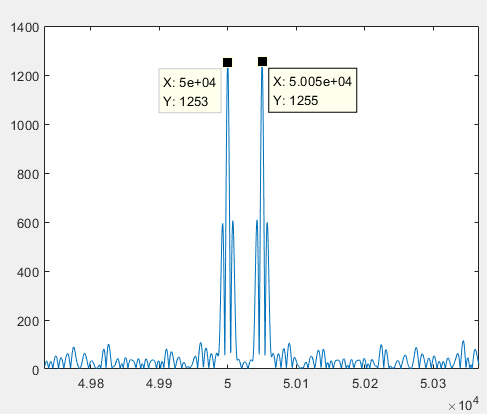
仿真时,考虑某个脉冲的多目标分辨性能。中心载频3GHz,脉冲重复间隔1ms,脉宽4us,相位BPSK编码调制,码宽0.1us,目标1距离50km,目标2距离50km+50m。脉冲回波信号如上图所示,右图为左图脉冲回波的放大图,此时目标分辨不出来。下图是经过脉冲压缩后的结果,目标能够分辨,并且距离分辨率由脉冲带宽决定,约为
二、线性调频雷达的相参与非相参
波形特点:一系列调频率参数相同的线性调频脉冲串信号,脉冲波形具有一定的占空比,发射波形为:
其中为初相,则接收信号波形为:
其中
仿真时,考虑某个脉冲的多目标分辨性能。中心载频GHz,脉冲重复间隔1ms,脉宽4us,调频率2.5e12 Hz/s,目标距离50km,速度10m/s。
- 当初相
固定(相参)
下图分别为距离脉压后的图像以及最终距离多普勒图像。
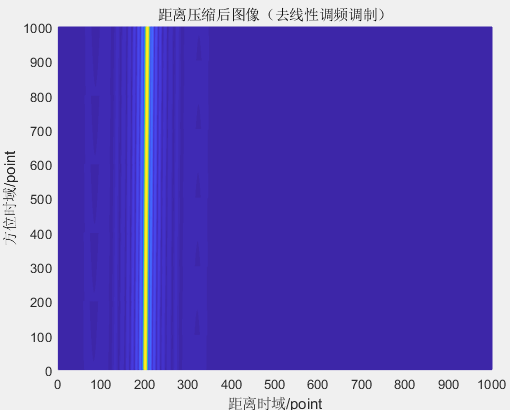
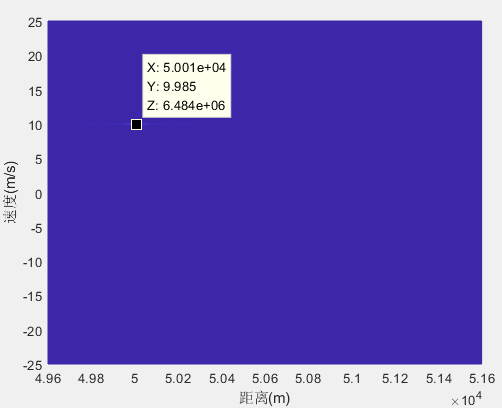
-
当初相
随机(非相参)
下图分别为距离脉压后的图像以及最终距离多普勒图像。可以看出非相参下,多普勒频率(速度)难以聚焦。
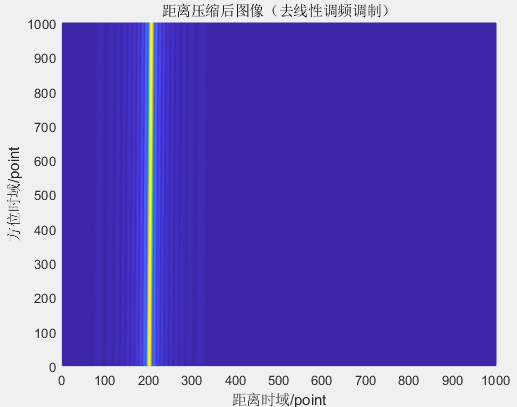
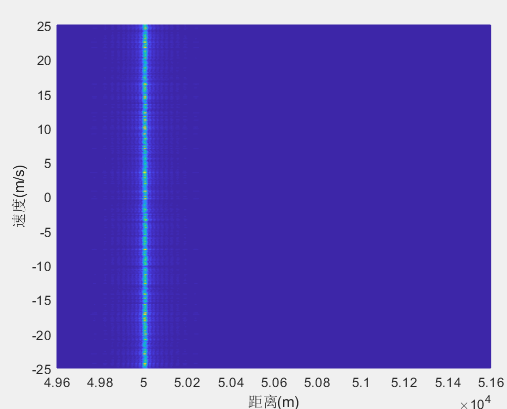
代码见雷达领域+波形设计+脉冲雷达体制
总结
本文主要对常见脉冲雷达的分辨性能进行了仿真,并通过仿真对比简单分析了相参体制在形成目标距离速度图像时的重要性。 转载请附链接【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主
相关文章:

信号类型(雷达)——脉冲雷达(三)
系列文章目录 《信号类型(雷达通信)》 《信号类型(雷达)——雷达波形认识(一)》 《信号类型(雷达)——连续波雷达(二)》 文章目录 前言 一、相参雷达 1…...
并查集(13张图解)--擒贼先擒王
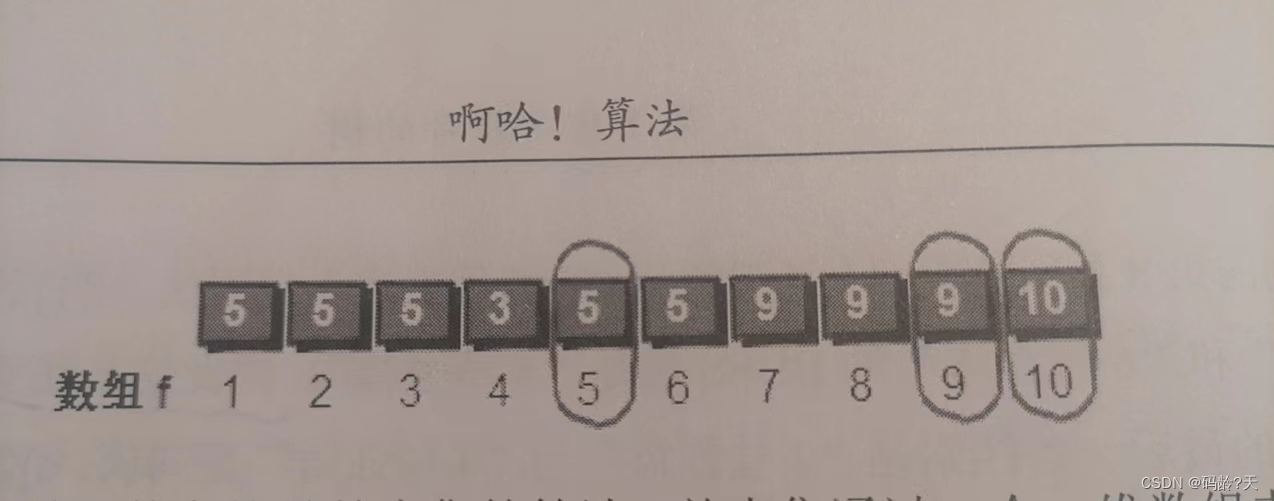
目录 前言 故事 🌼思路 🌼总结 🌼代码 👊观察过程代码 👊正确代码 👊细节代码 来自《啊哈算法》 前言 刚学了树在优先队列中的应用--堆的实现 那么树还有哪些神奇的用法呢?我们从一…...
Flutter3引用原生播放器-IOS(Swift)篇
前言由于Flutter项目中需要使用到播放器功能,因此对flutter中各种播放器解决方案进行了一番研究和比对,最后决定还是自己通过Plugin的方法去引用原生播放器符合自己的需求,本篇文章会对各种解决方案做一个简单的比较,以及讲解一下…...
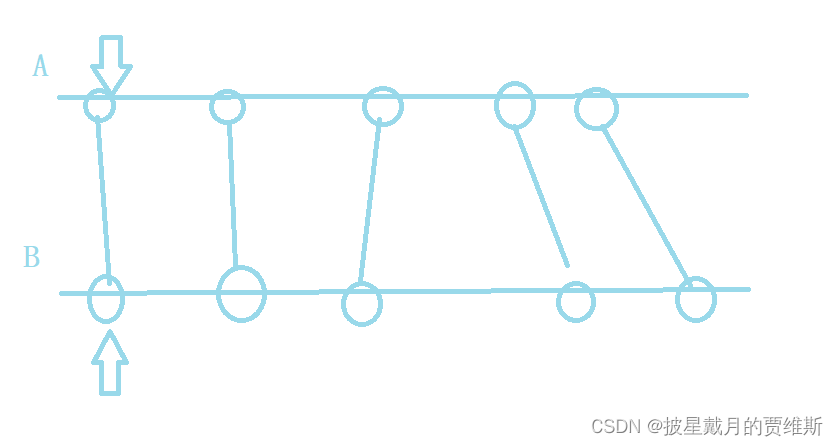
【蓝桥杯每日一题】双指针算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...
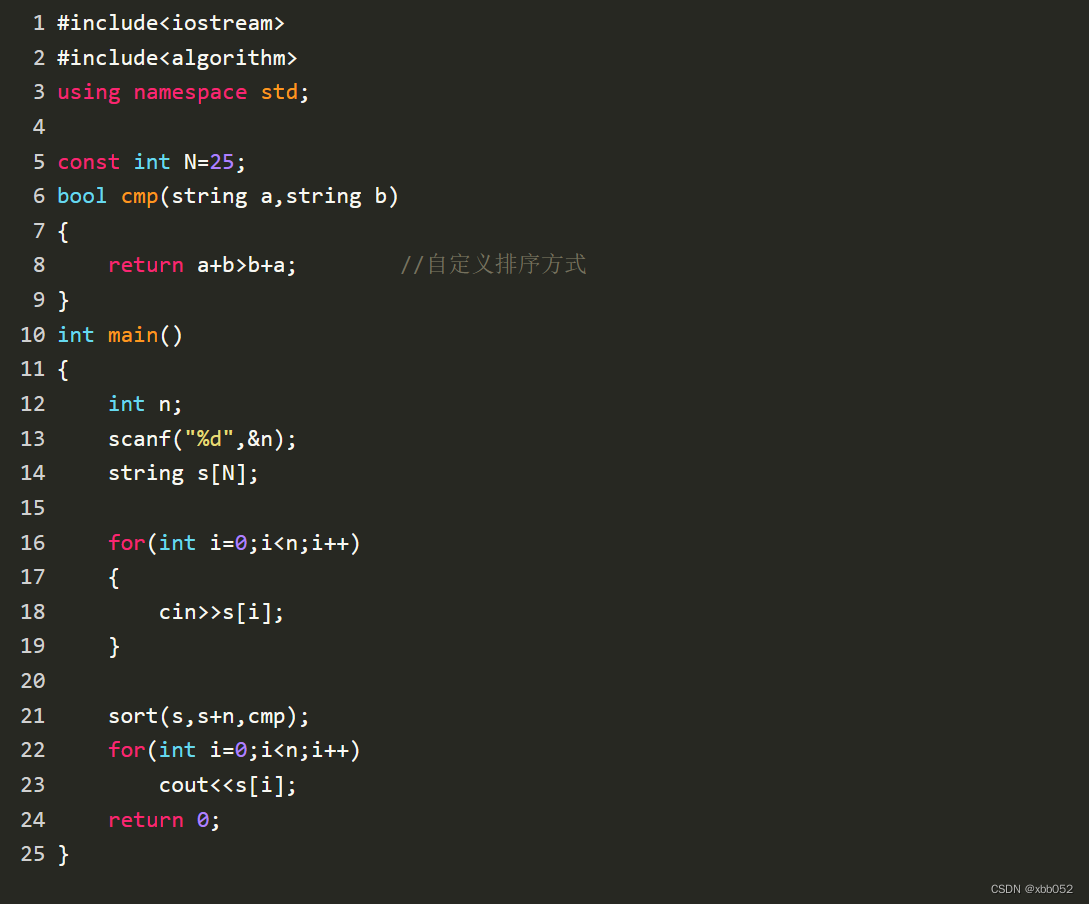
拼数(一般贪心)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题号:NC16783 时间限制:C/C 1秒,其他语言2秒 空间限制:C/C 262144K,其他语言524288K 64bit IO Format: %lld 题目描述 设有n个正整…...

LeetCode 热题 C++ 169. 多数元素 10. 正则表达式匹配 155. 最小栈
力扣169 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3] 输出࿱…...
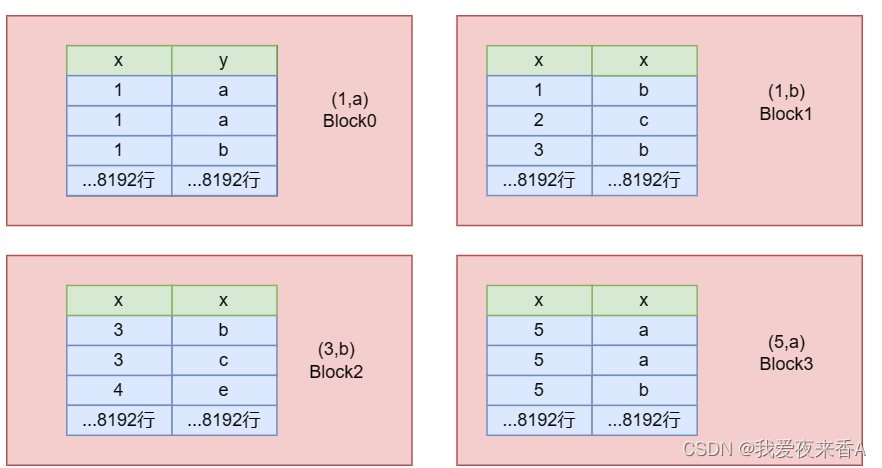
Clickhouse学习:MergeTree
MergeTree一、MergeTree逻辑存储结构二、MergeTree物理存储结构三、总结一、MergeTree逻辑存储结构 如上图所示,在排序键(CountrID、Date)上做索引,数据会按照这两个字段先后排序ClickHouse是稀疏索引,每隔8192行做一个索引,如(a,1),(a,2),比如想查a,要读取[0,3)之间的内容,稀疏…...
【java基础】包装类,自动装箱和自动拆箱
文章目录基本介绍包装类自动装箱自动拆箱包装类注意事项包装类比较包装器内容不可变基本介绍 有时,需要将int这样的基本类型转换为对象。所有的基本类型都有一个与之对应的类。 例如,Integer类对应基本类型int。通常,这些类称为包装器&#…...
Android笔记(二十五):两种sdk热更插件资源加载方案
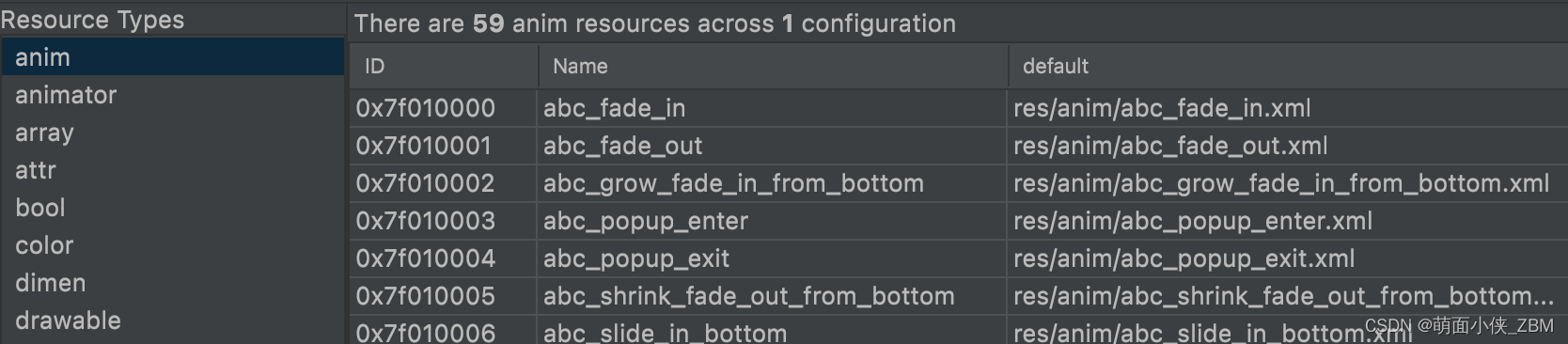
背景 在研究sdk插件化热更新方式的过程中总结出了两套插件资源加载方案,在此记录下 资源热更方式 方式一:合并所有插件资源 需要解决资源id冲突问题 资源ID值一共4个字段,由三部分组成:PackageIdTypeIdEntryId PackageId&…...

spring框架--全面详解(学习笔记)
目录 1.Spring是什么 2.Spring 框架特点 3.Spring体系结构 4.Spring开发环境搭建 5.spring中IOC和DI 6.Spring中bean的生命周期 7.Spring Bean作用域 8.spring注解开发 9.Spring框架中AOP(Aspect Oriented Programming) 10.AOP 实现分类 11.A…...
)
2023年CDGA考试模拟题库(401-500)
2023年CDGA考试模拟题库(401-500) 401.数据管理战略的SMART原则指的是哪项? [1分] A.具体 、高质量、可操作 、现实、有时间限制 B.具体、可衡量、可检验、现实、有时间限制 C.具体、可衡量、可操作、现实、有时间限制 D.具体、高质量、可检验、现实12-24个月的目标 答…...

软件设计师备考文档
cpu 计算机的基本硬件系统:运算器、控制器、存储器、输入设备、输出设备 cpu负责获取程序指令,对指令进行译码并加以执行 * cpu的功能控制器(保证程序正常执行,处理异常事件) 程序控制操作控制运算器(只能…...
)
Javascript的API基本内容(一)
一、获取DOM对象 querySelector 满足条件的第一个元素 querySelectorAll 满足条件的元素集合 返回伪数组 document.getElementById 专门获取元素类型节点,根据标签的 id 属性查找 二、操作元素内容 通过修改 DOM 的文本内容,动态改变网页的内容。 inn…...

10、最小公倍数
法一: #include <stdio.h>int main(){int a,b;scanf("%d%d",&a,&b);int m a>b?a:b;//m表示a,b之间的较大值while(1){if(m%a0&&m%b0){break;}m;}printf("%d",m);return 0; }法二:a*i%b0成立 #include &…...

【vue】vue2.x项目中使用md文件
一、Vue项目展示md文件的三种方式 1、将md文件 导入为 html 生成的标题标签自带具有id属性,值为标题内容; <h2 id"测试">测试</h2> # 处理md为html字符串 yarn add markdown-loader # 处理字符串,用于导出显示 yarn a…...

操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 注:阅读本编文章前,请先阅读系列文章,以免造成看不懂的情况!! MSF和CS绕过UAC提权 CS绕过UAC提权 拿到一个普通管理员的SHELL,在CS中没有*号代表有…...

快速排序+快速定位
快速排序算法采用了分治法以及递归作为解决问题的思想。在计算机科学中,分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以…...

nginx http rewrite module 详解
大家好,我是 17。 今天和大家聊聊 nginx http rewrite module 。 简单来说, ngx_http_rewrite_module module 用正则匹配请求,改写请求,然后做跳转。可以是内部跳转,也可以是外部跳转。 学习这个模块的时候…...

机器学习可解释性一(LIME)
随着深度学习的发展,越来越多的模型诞生,并且在训练集和测试集上的表现甚至于高于人类,但是深度学习一直被认为是一个黑盒模型,我们通俗的认为,经过训练后,机器学习到了数据中的特征,进而可以正…...

CV学习笔记-MobileNet
MobileNet 文章目录MobileNet1. MobileNet概述2. 深度可分离卷积(depthwise separable convolution)2.1 深度可分离卷积通俗理解2.2 深度可分离卷积对于参数的优化3. MobileNet网络结构4. 代码实现4.1 卷积块4.2 深度可分离卷积块4.3 MobileNet定义4.4 完…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
