深度学习(生成式模型)——DDIM:Denoising Diffusion Implicit Models
文章目录
- 前言
- 为什么DDPM的反向过程与前向过程步数绑定
- DDIM如何减少DDPM反向过程步数
- DDIM的优化目标
- DDIM的训练与测试
前言
上一篇博文介绍了DDIM的前身DDPM。DDPM的反向过程与前向过程步数一一对应,例如前向过程有1000步,那么反向过程也需要有1000步,这导致DDPM生成图像的效率非常缓慢。本文介绍的DDIM将降低反向过程的推断步数,从而提高生成图像的效率。
值得一提的是,DDIM的反向过程仍然是马尔可夫链,但论文里有讨论非马尔可夫链的生成模型。本博文只总结DDIM如何提高DDPM的生成图像效率。
为什么DDPM的反向过程与前向过程步数绑定
DDPM反向过程的推导公式为
q ( x ^ t − 1 ∣ x ^ t ) = q ( x ^ t − 1 ∣ x ^ t , x ^ 0 ) = q ( x ^ t − 1 , x ^ t , x ^ 0 ) q ( x ^ t , x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 , x ^ 0 ) q ( x ^ t − 1 , x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) q ( x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 , x ^ 0 ) q ( x ^ t − 1 ∣ x ^ 0 ) q ( x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) q ( x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 , x ^ 0 ) q ( x ^ t − 1 ∣ x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 ) q ( x ^ t − 1 ∣ x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) \begin{aligned} q(\hat x_{t-1}|\hat x_{t})&=q(\hat x_{t-1}|\hat x_{t},\hat x_0)\\ &=\frac{q(\hat x_{t-1},\hat x_t,\hat x_0)}{q(\hat x_t,\hat x_0)}\\ &=\frac{q(\hat x_{t}|\hat x_{t-1},\hat x_0)q(\hat x_{t-1},\hat x_0)}{q(\hat x_t|\hat x_0)q(\hat x_0)}\\ &=\frac{q(\hat x_{t}|\hat x_{t-1},\hat x_0)q(\hat x_{t-1}|\hat x_0)q(\hat x_0)}{q(\hat x_t|\hat x_0)q(\hat x_0)}\\ &=\frac{q(\hat x_{t}|\hat x_{t-1},\hat x_0)q(\hat x_{t-1}|\hat x_0)}{q(\hat x_t|\hat x_0)}\\ &=\frac{ q(\hat x_{t}|\hat x_{t-1})q(\hat x_{t-1}|\hat x_0)}{q(\hat x_t|\hat x_0)} \end{aligned} q(x^t−1∣x^t)=q(x^t−1∣x^t,x^0)=q(x^t,x^0)q(x^t−1,x^t,x^0)=q(x^t∣x^0)q(x^0)q(x^t∣x^t−1,x^0)q(x^t−1,x^0)=q(x^t∣x^0)q(x^0)q(x^t∣x^t−1,x^0)q(x^t−1∣x^0)q(x^0)=q(x^t∣x^0)q(x^t∣x^t−1,x^0)q(x^t−1∣x^0)=q(x^t∣x^0)q(x^t∣x^t−1)q(x^t−1∣x^0)
值得一提的是,反向过程的马尔可夫状态 x ^ t \hat x_t x^t、 x ^ t − 1 \hat x_{t-1} x^t−1不一定要与前向过程一致,如下图所示,反向过程的状态 x ^ T \hat x_T x^T、 x ^ T − 1 \hat x_{T-1} x^T−1对应前向过程的 x T x_T xT、 x T − 2 x_{T-2} xT−2。

从上述公式构成来看,反向过程的概率图形式与 q ( x ^ t ∣ x ^ t − 1 ) q(\hat x_t|\hat x_{t-1}) q(x^t∣x^t−1)有关。而在DDPM中, q ( x ^ t ∣ x ^ t − 1 ) q(\hat x_t|\hat x_{t-1}) q(x^t∣x^t−1)与前向过程 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)一致,这就导致DDPM的概率图为

因此利用DDPM推导的 q ( x ^ t − 1 ∣ x ^ t ) q(\hat x_{t-1}|\hat x_{t}) q(x^t−1∣x^t)进行反向过程时,状态转移步数必须与前向过程一致。
DDIM如何减少DDPM反向过程步数
在上一节中,我们说明了反向过程的马尔可夫状态与前向过程不需要一致,这表明 q ( x ^ t − 1 ∣ x ^ t ) q(\hat x_{t-1}|\hat x_{t}) q(x^t−1∣x^t)的概率密度函数有多种。找到合适的概率密度函数,我们即可减少反向过程的迭代步数,同时保持生成图像的质量,这便是DDIM的出发点。以下的推导中,我们将用 x t 、 x t − 1 x_t、x_{t-1} xt、xt−1来表示反向过程的马尔可夫状态。
本章节的所有符号定义与深度学习(生成式模型)——DDPM:denoising diffusion probabilistic models一致
为了书写方便,除非特殊提及,在以下的所有推导中,所有的 x x x、 ϵ \epsilon ϵ符号都表示随机变量,而不是一个样本。
在DDPM的前向过程里有
x t − 1 = α ˉ t x 0 + 1 − α ˉ t ϵ t − 1 (2.0) \begin{aligned} x_{t-1}&=\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon_{t-1}\tag{2.0} \end{aligned} xt−1=αˉtx0+1−αˉtϵt−1(2.0)
已知两个均值为0的高斯分布相加具备以下性质
N ( 0 , δ 1 2 ) + N ( 0 , δ 2 2 ) = N ( 0 , δ 1 2 + δ 2 2 ) \mathcal N(0,\delta_1^2)+\mathcal N(0,\delta_2^2)=\mathcal N(0,\delta_1^2+\delta_2^2) N(0,δ12)+N(0,δ22)=N(0,δ12+δ22)
依据重参数化技巧,已知
1 − α ˉ t − δ t 2 ϵ t ∼ N ( 0 , 1 − α ˉ t − δ t 2 ) δ t ϵ ∼ N ( 0 , δ t 2 ) 1 − α ˉ ϵ t − 1 ∼ N ( 0 , 1 − α ˉ t − 1 ) \begin{aligned} \sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_{t}&\sim \mathcal N(0,1-\bar\alpha_{t}-\delta_t^2)\\ \delta_t\epsilon&\sim \mathcal N(0,\delta_t^2)\\ \sqrt{1-\bar\alpha}\epsilon_{t-1}&\sim \mathcal N(0,1-\bar \alpha_{t-1}) \end{aligned} 1−αˉt−δt2ϵtδtϵ1−αˉϵt−1∼N(0,1−αˉt−δt2)∼N(0,δt2)∼N(0,1−αˉt−1)
则有
x t − 1 = α ˉ t − 1 x 0 + 1 − α ˉ t ϵ t − 1 = α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 ϵ t + δ t ϵ = α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 x t − α ˉ t x 0 1 − α ˉ t + δ t ϵ (2.1) \begin{aligned} x_{t-1}&=\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_t}\epsilon_{t-1}\\ &=\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_{t}+\delta_t\epsilon\\ &=\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\frac{x_t-\sqrt{\bar \alpha_t}x_0}{\sqrt{1-\bar\alpha_t}}+\delta_t\epsilon \end{aligned}\tag{2.1} xt−1=αˉt−1x0+1−αˉtϵt−1=αˉt−1x0+1−αˉt−δt2ϵt+δtϵ=αˉt−1x0+1−αˉt−δt21−αˉtxt−αˉtx0+δtϵ(2.1)
依据重参数化公式,式2.1可表征为
q ( x t − 1 ∣ x t ) = q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 x t − α ˉ t x 0 1 − α ˉ t , δ t 2 I ) (2.2) \begin{aligned} q(x_{t-1}|x_{t})&=q(x_{t-1}|x_t,x_0)\\ &=\mathcal N(x_{t-1};\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\frac{x_t-\sqrt{\bar \alpha_t}x_0}{\sqrt{1-\bar\alpha_t}},\delta_t^2\mathcal I)\tag{2.2} \end{aligned} q(xt−1∣xt)=q(xt−1∣xt,x0)=N(xt−1;αˉt−1x0+1−αˉt−δt21−αˉtxt−αˉtx0,δt2I)(2.2)
注意式2.2的推导过程绕过了贝叶斯公式,而且没有指定反向过程的状态转移图,因此式2.1是一个反向过程的概率密度函数族,不同的 δ t \delta_t δt表示不同的概率密度函数,对应反向过程不同的马尔可夫状态转移链。
结合式2.0,式2.2可进一步变化为
q ( x t − 1 ∣ x t ) = q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; α ˉ t − 1 x t − 1 − α ˉ t ϵ t α ˉ t + 1 − α ˉ t − δ t 2 ϵ t , δ t 2 I ) (2.3) \begin{aligned} q(x_{t-1}|x_t)&=q(x_{t-1}|x_t,x_0)\\ &=N(x_{t-1};\sqrt{\bar \alpha_{t-1}}\frac{x_t-\sqrt{1-\bar \alpha_t}\epsilon_t}{\sqrt{\bar\alpha_t}}+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_t,\delta_t^2\mathcal I)\tag{2.3} \end{aligned} q(xt−1∣xt)=q(xt−1∣xt,x0)=N(xt−1;αˉt−1αˉtxt−1−αˉtϵt+1−αˉt−δt2ϵt,δt2I)(2.3)
DDIM的优化目标
由于DDIM与DDPM一样,前向过程与反向过程均为马尔科夫链,因此优化目标也一致。从上一篇博客,我们可知DDPM的优化目标为
L = ∑ t = 2 T D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) = ∑ t = 2 T ( 1 2 ( n + 1 δ t 2 ∣ ∣ μ t − μ θ ∣ ∣ 2 − n + l o g 1 ) = ∑ t = 2 T ( 1 2 δ t 2 ∣ ∣ μ t − μ θ ∣ ∣ 2 ) \begin{aligned} L&=\sum_{t=2}^TD_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))\\ &=\sum_{t=2}^T(\frac{1}{2}(n+\frac{1}{\delta_t^2}||\mu_t-\mu_\theta||^2-n+log1)\\ &=\sum_{t=2}^T(\frac{1}{2\delta_t^2}||\mu_t-\mu_\theta||^2)\\ \end{aligned} L=t=2∑TDKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))=t=2∑T(21(n+δt21∣∣μt−μθ∣∣2−n+log1)=t=2∑T(2δt21∣∣μt−μθ∣∣2)
设网络预测的噪声为 ϵ θ ( x t ) \epsilon_\theta(x_t) ϵθ(xt),则DDIM的优化目标为:
L = ∑ t = 2 T ( 1 2 δ t 2 ∣ ∣ μ t − μ θ ∣ ∣ 2 ) = ∑ t = 2 T ( 1 2 δ 2 ∣ ∣ α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 ϵ t − ( α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 ϵ θ ( x t ) ) ∣ ∣ 2 ) = ∑ t = 2 T ( 1 − α ˉ t − δ t 2 2 δ t 2 ∣ ∣ ϵ t − ϵ θ ( x t ) ∣ ∣ 2 ) \begin{aligned} L&=\sum_{t=2}^T(\frac{1}{2\delta_t^2}||\mu_t-\mu_\theta||^2)\\ &=\sum_{t=2}^T(\frac{1}{2\delta^2}||\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_t-(\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_\theta(x_t))||^2)\\ &=\sum_{t=2}^T(\frac{1-\bar\alpha_t-\delta_t^2}{2\delta_t^2}||\epsilon_t-\epsilon_{\theta}(x_t)||^2) \end{aligned} L=t=2∑T(2δt21∣∣μt−μθ∣∣2)=t=2∑T(2δ21∣∣αˉt−1x0+1−αˉt−δt2ϵt−(αˉt−1x0+1−αˉt−δt2ϵθ(xt))∣∣2)=t=2∑T(2δt21−αˉt−δt2∣∣ϵt−ϵθ(xt)∣∣2)
结合上式以及坐标下降法,可得DDIM最终优化目标 L L L为
L = ∣ ∣ ϵ t − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t ) ∣ ∣ 2 L=||\epsilon_t-\epsilon_\theta(\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon_t)||^2 L=∣∣ϵt−ϵθ(αˉtx0+1−αˉtϵt)∣∣2
与DDPM一致
DDIM的训练与测试
DDIM的训练过程与DDPM一致,反向过程的采样公式变为
x t − 1 = α ˉ t − 1 x t − 1 − α ˉ t ϵ θ ( x t ) α ˉ t + 1 − α ˉ t − δ t 2 ϵ θ ( x t ) + δ t ϵ (4.0) x_{t-1}=\sqrt{\bar \alpha_{t-1}}\frac{x_t-\sqrt{1-\bar \alpha_t}\epsilon_\theta(x_t)}{\sqrt{\bar\alpha_t}}+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_\theta(x_t)+\delta_t\epsilon\tag{4.0} xt−1=αˉt−1αˉtxt−1−αˉtϵθ(xt)+1−αˉt−δt2ϵθ(xt)+δtϵ(4.0)
其中 ϵ \epsilon ϵ从标准正态分布中采样得到, δ t \delta_t δt为超参数,其取值为
δ t = η ( 1 − α ˉ t − 1 ) / ( 1 − α ˉ t ) 1 − α ˉ t / α ˉ t − 1 \delta_t=\eta\sqrt{(1-\bar\alpha_{t-1})/(1-\bar\alpha_{t})}\sqrt{1-\bar\alpha_t/\bar\alpha_{t-1}} δt=η(1−αˉt−1)/(1−αˉt)1−αˉt/αˉt−1
特别的,当 η = 1 \eta=1 η=1时,DDIM的反向过程与DDPM一致。当 η = 0 \eta=0 η=0时,式4.0的 ϵ \epsilon ϵ将被去掉,从而不具备随机性。即反向过程步数固定情况下,从一个噪声生成的图片将是确定,DDIM一般将 η \eta η取值设为0。
具体的实验结果可见下图:
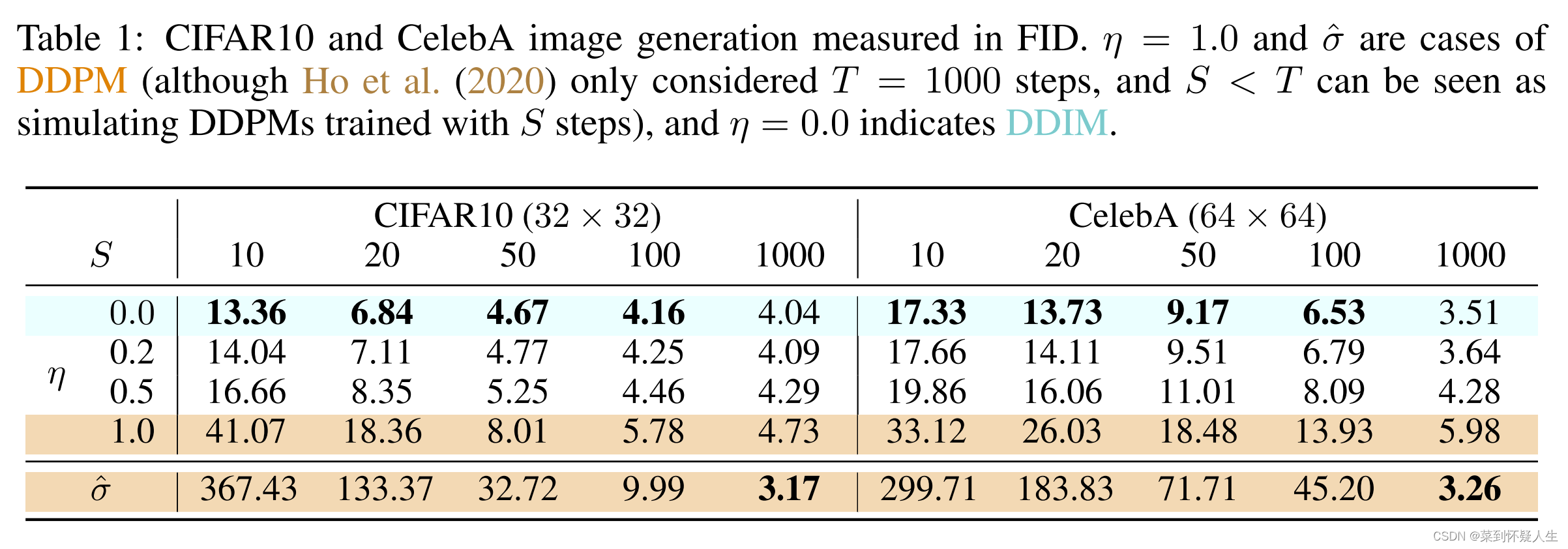
相关文章:

深度学习(生成式模型)——DDIM:Denoising Diffusion Implicit Models
文章目录 前言为什么DDPM的反向过程与前向过程步数绑定DDIM如何减少DDPM反向过程步数DDIM的优化目标DDIM的训练与测试 前言 上一篇博文介绍了DDIM的前身DDPM。DDPM的反向过程与前向过程步数一一对应,例如前向过程有1000步,那么反向过程也需要有1000步&a…...

HashMap的遍历方式 -- 好几次差点记不起来总结了一下
public class HashMapDemo {public static void main(String[] args) {// 创建一个HashMap并添加一些键值对Map<String, Integer> hashMap new HashMap<>();hashMap.put("Alice", 25);hashMap.put("Bob", 30);hashMap.put("Charlie"…...

PostgreSQL 两表关联更新sql
PostgreSQL两表关联更新SQL如下: UPDATE user SET username ft.name, age ft.age FROM userinfo WHERE user.id ft.id; user 要更新的表 userinfo数据来源表...
R2R 的一些小tip
批次间控制器(Run-to-run Controller),以应对高混合生产的挑战。将最优配方参数与各种工业特征相关联的模型是根据历史数据离线训练的。预测的最优配方参数在线用于调整工艺条件。 批次控制(R2R control)是一种先进的工艺控制技术,可在运行(如批次或晶圆…...

UML中类之间的六种主要关系
UML中类之间的六种主要关系: 继承(泛化)(Inheritance、Generalization), 实现(Realization),关联(Association),聚合(Aggregation),组…...

机器学习-朴素贝叶斯之多项式模型
多项式模型: 记住一定用于离散的对象,不能是连续的 于高斯分布相反,多项式模型主要适用于离散特征的概率计算,切sklearn的多项式模型不接受输入负值 因为多项式不接受负值的输入,所以样本数据的特征为数值型数据&…...

下载的nginx证书转换成tomcat证书格式
1、下载的nginx证书格式 XXX.crt private.key 2、转换成JKS格式证书步骤 #crt格式证书转pem openssl x509 -in xxx.crt -out xxx.pem#先转成p12格式,此时注意,如果有别名,需要设置 openssl pkcs12 -export -in xxx.crt -inkey private.key…...
计算机毕业设计选题推荐-社区志愿者服务微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

ES6中数值扩展
目录 二进制和八进制表示法 Number.isFinite() Number.isNaN() Number.parseInt()和Number.parseFloat() Number.isInteger() Math.trunc() Math.sign() Math.cbrt(): Math.clz32(): Math.imul(): Math.fround(): ES6中…...
sql-50练习题11-15
sql-50练习题11-15 前言数据库表结构介绍学生表课程表成绩表教师表 1-1 查询没有学全所有课程的同学的信息1-2 查询至少有一门课与学号为01的同学所学相同的同学的信息1-3 查询和1号的同学学习的课程完全相同的其他同学的信息1-4 查询没学过张三老师讲授的任一门课程的学生姓名…...
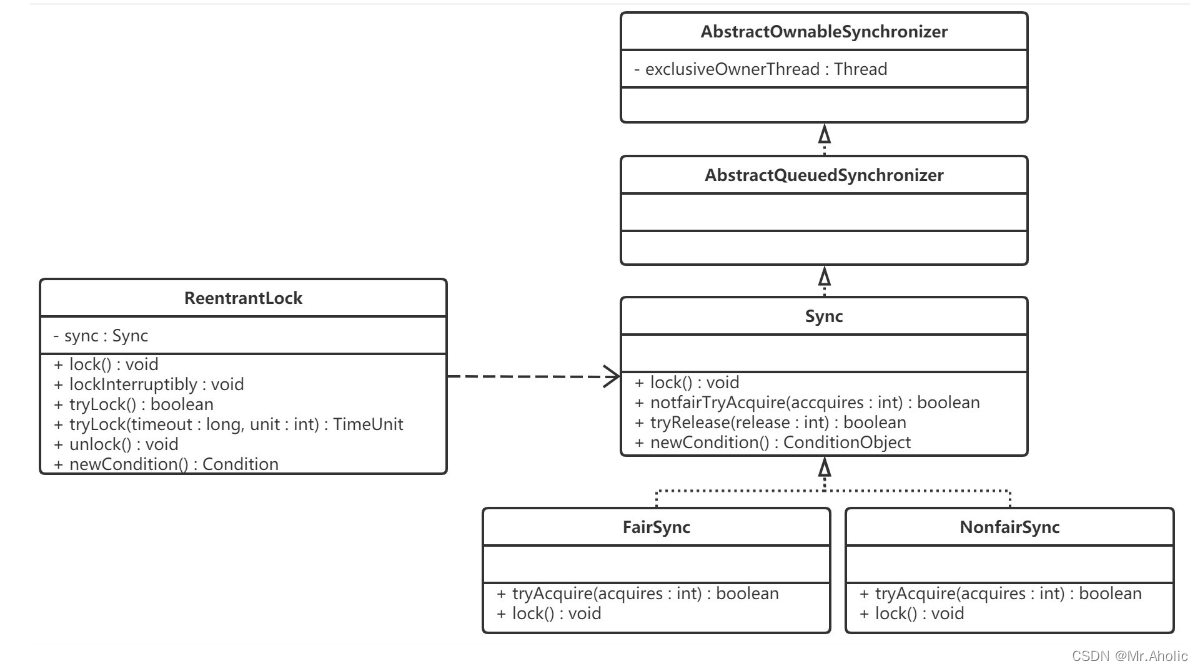
【多线程面试题十九】、 公平锁与非公平锁是怎么实现的?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官: 公平锁与非公平锁是怎么…...
LabVIEW背景颜色设为和其他程序或图像中一样
LabVIEW背景颜色设为和其他程序或图像中一样 有时候LabVIEW背景色要和其他程序或者图片的颜色保持一致,如果要求不高可以大致设置一下。如果要求较高,那可以按照如下的方式。 先用PS打开标准图像,之后用吸管工具选择图像上中的点࿰…...

图表参考线,数据对比一目了然_三叠云
参考线 路径 仪表盘 >> 仪表盘设计 功能简介 新增「参考线」功能。 参考线是在单个图表组件中添加的一条水平虚线,也可以配置两条线形成的参考区间,它表示该水平线上纵坐标值的大小。 使用场景: 通过辅助线的设置,可…...
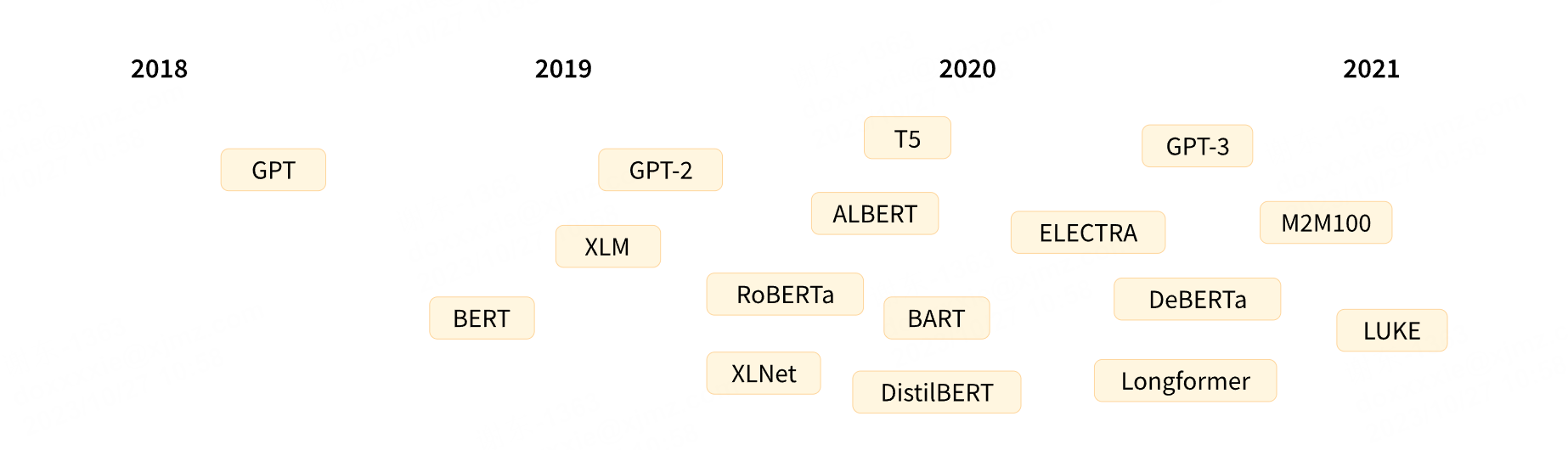
【深度学习】Transformer、GPT、BERT、Seq2Seq什么区别?
请看vcr:https://transformers.run/back/transformer/...
)
数据结构与算法之LRU: 实现 LRU 缓存算法功能 (Javascript版)
关于LRU缓存 LRU - Lease Recently Used 最近使用 如果内存优先,只缓存最近使用的,删除 ‘沉睡’ 数据 核心 api: get set 分析 使用哈希表来实现, O(1)必须是有序的,常用放在前面,沉睡放在后面, 即:有序࿰…...

Matlab | 基于二次谱提取地震数据的地震子波
本文通过地震数据二次谱求取地震子波谱,具体方法如下: MATLAB代码实现如下: function w SndSpecExtWavelet(x, M) % 功能:基于二次谱提取输入地震数据data的地震子波wavelet % Extracting Wavelet from Input Seismic Dat…...
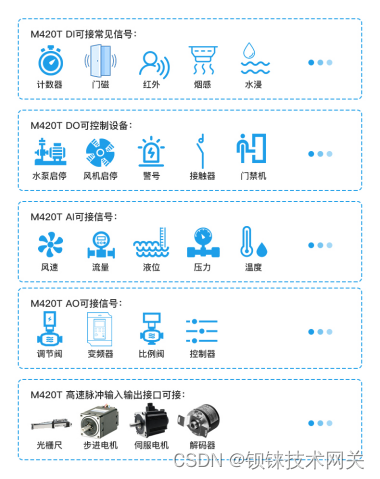
利用远程IO模块,轻松驾驭食品包装生产的自动化
常见的自动化包装系统,它的核心部分通常由一系列高端设备组成,包括自动开箱机、自动封箱机、自动捆扎机、装箱机器人、码垛机器人等。这些设备协同工作,形成一条高效运转的生产线,从开箱到装箱,再到码垛,每…...
华为OD机考算法题:计算最大乘积
题目部分 题目计算最大乘积难度易题目说明给定一个元素类型为小写字符串的数组,请计算两个没有相同字符的元素长度乘积的最大值。 如果没有符合条件的两个元素,返回 0。输入描述输入为一个半角逗号分隔的小写字符串的数组,2< 数组长度<…...
用友 GRP-U8 存在sql注入漏洞复现
0x01 漏洞介绍 用友 GRP-U8 license_check.jsp 存在sql注入,攻击者可利用该漏洞执行任意SQL语句,如查询数据、下载数据、写入webshell、执行系统命令以及绕过登录限制等。 fofa:app”用友-GRP-U8” 0x02 POC: /u8qx/license_check.jsp?kj…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

