2023NOIP A层联测20-点餐
一家新的餐馆开业了,为了吸引更多的顾客,每样餐品都有打折的活动。特别的,餐馆内一共有𝑛样菜品,编号从 1 1 1 到 n n n,每样菜品每人最多只能点一次。对于第 i i i 种菜品,其包含两种价格:活动价格 a i a_i ai 与差价 b i b_i bi。
假设某顾客点了 k k k 样菜品,依次编号为 p 1 , … , p k p_1,\dots,p_k p1,…,pk,那么最终需要支付的价格为
∑ i = 1 k a p i + max i = 1 k b p i \sum\limits_{i=1}^ka_{p_i}+\max_{i=1}^kb_{p_i} i=1∑kapi+i=1maxkbpi
现在有 n n n 名顾客光顾这家餐馆,第 i i i 名顾客想恰好点 i i i 样菜品,请帮助每位顾客计算出他的最小花费。
n ≤ 2 × 1 0 5 n\le2\times10^5 n≤2×105
先把菜品按 b b b 从小到大排序,如果当前要点 k k k 个菜,选定第 i i i 个菜,那么就是要在前 i − 1 i-1 i−1 个菜中选 k − 1 k-1 k−1 个菜。
可以用 set 维护,或者主席树,时间复杂度 O ( n 2 log n ) O(n^2\log n) O(n2logn),这是暴力。
设 w ( k , i ) w(k,i) w(k,i) 表示前 i i i 个菜中选 k k k 个菜的最小花费, f ( k ) f(k) f(k) 为使 w ( k , i ) w(k,i) w(k,i) 取得最小值的 i i i。
考虑决策 x < y x<y x<y,若 w ( k , x ) ≥ w ( k , y ) w(k,x)\ge w(k,y) w(k,x)≥w(k,y),增大 k k k 后 y y y 可选的菜品比 x x x 的多,所以 ∀ k ′ ∈ ( k , n ] , w ( k ′ , x ) ≥ w ( k ′ , y ) \forall k'\in(k,n],w(k',x)\ge w(k',y) ∀k′∈(k,n],w(k′,x)≥w(k′,y),若 y = f ( k ) y=f(k) y=f(k),则对于后面的决策点 m m m, w w w 值至少都比前面的要小了,所以 f ( k ) ≤ f ( m ) f(k)\le f(m) f(k)≤f(m),即 f ( 1 ) ≤ f ( 2 ) ≤ ⋯ ≤ f ( n ) f(1)\le f(2)\le\dots\le f(n) f(1)≤f(2)≤⋯≤f(n),决策具有单调性。
如果这是 DP,就可以用 1D/1D 动态规划的优化方法 O ( n log n ) O(n\log n) O(nlogn) 拿下。但是这不是。
这里要用分治的思想,函数 s o l v e ( l , r , L , R ) solve(l,r,L,R) solve(l,r,L,R) 表示当前处理到区间 [ l , r ] [l,r] [l,r], m i d mid mid 的最优决策点在 L , R L,R L,R。每次暴力求出 p o s = f ( m i d ) pos=f(mid) pos=f(mid),把问题分成 s o l v e ( l , m i d − 1 , L , p o s ) solve(l,mid-1,L,pos) solve(l,mid−1,L,pos) 和 s o l v e ( m i d + 1 , r , p o s , R ) solve(mid+1,r,pos,R) solve(mid+1,r,pos,R) 两部分,这样递归处理下去。
求一个 w w w 是 O ( log V ) O(\log V) O(logV) 的,总的时间复杂度为 O ( n log n log V ) O(n\log n\log V) O(nlognlogV)。( V V V 是值域)
代码如下
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll INF=1e18,Inf=1e9;
const int N=2e5+1;
int n,A[N],cnt,rt[N];
ll ans[N];
struct node
{int a,b;bool operator<(const node &a)const{return b<a.b;}
}a[N];
struct Node
{int ls,rs,sz;ll sum;
}tr[N*32];
void insert(int &rt,int la,int l,int r,int x)
{rt=++cnt;tr[rt]=tr[la];tr[rt].sz++;tr[rt].sum+=x;if(l==r) return;int mid=l+r>>1;if(x<=mid) insert(tr[rt].ls,tr[la].ls,l,mid,x);else insert(tr[rt].rs,tr[la].rs,mid+1,r,x);
}
ll query(int rt,int l,int r,int k)
{if(l==r) return k*l;int mid=l+r>>1,sum=tr[tr[rt].ls].sz;if(sum>=k) return query(tr[rt].ls,l,mid,k);else return query(tr[rt].rs,mid+1,r,k-sum)+tr[tr[rt].ls].sum;
}
void solve(int l,int r,int L,int R)
{if(r<l) return;int mid=l+r>>1,pos;ll sum=INF;for(int i=max(mid,L);i<=R;i++){ll x=a[i].b+a[i].a+query(rt[i-1],0,Inf,mid-1);if(sum>x){sum=x;pos=i;}}ans[mid]=sum;solve(l,mid-1,L,pos);solve(mid+1,r,pos,R);
}
int main()
{freopen("order.in","r",stdin);freopen("order.out","w",stdout);scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d%d",&a[i].a,&a[i].b);sort(a+1,a+1+n);for(int i=1;i<=n;i++) insert(rt[i],rt[i-1],0,Inf,a[i].a);solve(1,n,1,n);for(int i=1;i<=n;i++) printf("%lld\n",ans[i]);
}
相关文章:

2023NOIP A层联测20-点餐
一家新的餐馆开业了,为了吸引更多的顾客,每样餐品都有打折的活动。特别的,餐馆内一共有𝑛样菜品,编号从 1 1 1 到 n n n,每样菜品每人最多只能点一次。对于第 i i i 种菜品,其包含两种价格&a…...

3D LUT 滤镜 shader 源码分析
最近在做滤镜相关的渲染学习,目前大部分 LUT 滤镜代码实现都是参考由 GPUImage 提供的 LookupFilter 的逻辑,整个代码实现不多。参考网上的博文也有各种解释,参考了大量博文之后终于理解了,所以自己重新整理了一份,方便…...
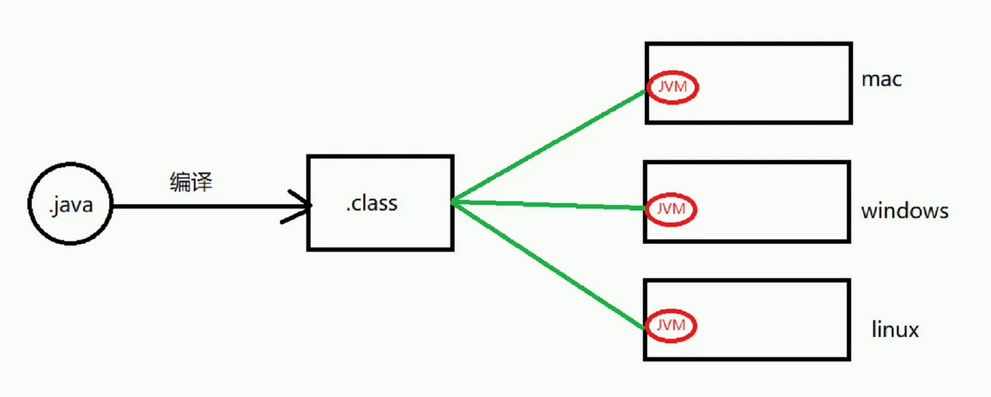
五分钟理解Java跨平台原理(适合小白)
JVM通俗的理解 Java语言的一个非常重要的特点就是与平台的无关性。而使用Java虚拟机,即JVM(Java Virtual Machine)是实现这一特点的关键。JVM是一种用于计算设备的规范,它是一个虚构出来的计算机,是通过在实际的计算机…...

从初级测试工程师到测试专家,你的晋升路线是什么?
最近,我们讨论了软件测试工程的的分级,大家都贡献了自己的想法。 对于大家来说,软件测试人的分级其实也代表了我们的进阶方向,职业发展。总体来说,测试工程师未来发展有三个方向: 技术精英 行业专家 管理…...

合肥中科深谷嵌入式项目实战——人工智能与机械臂(四)
订阅:新手可以订阅我的其他专栏。免费阶段订阅量1000 python项目实战 Python编程基础教程系列(零基础小白搬砖逆袭) 作者:爱吃饼干的小白鼠。Python领域优质创作者,2022年度博客新星top100入围,荣获多家平台专家称号。…...
Zynq-Linux移植学习笔记之64- 国产ZYNQ在linux下配置国产5396芯片
1、背景介绍 复旦微ZYNQ通过SPI配置国产JEM5396,框图如下: 现在需要在linux下的应用程序内配置JEM5396的寄存器。其中FMQL和进口的XILINX ZYNQ类似,JEM5396和进口的BCM5396兼容。因此可以参考进口ZYNQ在linux下配置BCM5396过程。Zynq-Linux移…...

系统架构设计师-第19章-大数据架构设计理论与实践-软考学习笔记
传统数据处理系统存在的问题 传统数据处理系统存在以下问题: 1. 数据孤岛问题:不同部门或系统之间的数据隔离,数据无法共享和整合。 2. 数据不一致性问题:由于数据维护分散,同一数据在不同系统或部门中可能存在不同…...
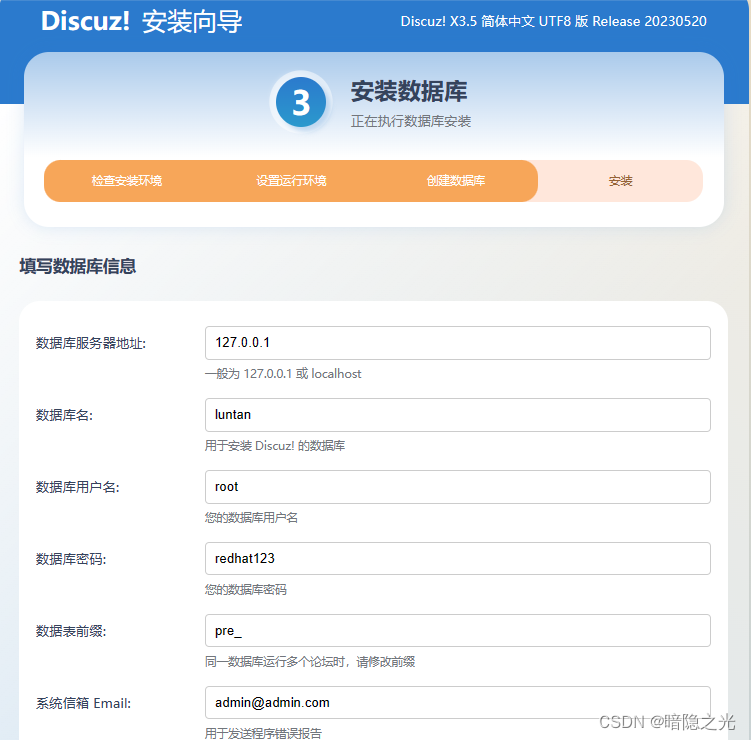
论坛搭建.
目录 一.配置软件仓库 二.安装http php miriadb 三.配置数据库 四.源码拖拽并解压 五.防火墙通过 六.浏览器安装测试 七.界面参数设置 一.配置软件仓库 1.进入仓库目录 cd /etc/yum.repos.d 2.创建仓库文件 vim local.repo 3.在 local.repo中写入:(粘贴的时候注意位…...

三种前端埋点方式
什么是埋点 埋点是数据采集领域(尤其是用户行为数据采集领域)的术语,指的是针对特定用户行为或事件进行捕获、处理和发送的相关技术及其实施过程。比如用户某个icon点击次数、观看某个视频的时长等等。 我们可以知道埋点实际上是对特定事件或…...

html获取网络数据,列表展示 第二种
html获取网络数据,列表展示 第二种 js遍历json数组中的json对象 image.png || - 判断数据是否为空,为空就显示 - <!DOCTYPE html> <html><head><meta charset"utf-8"><title>网页列表</title><script …...
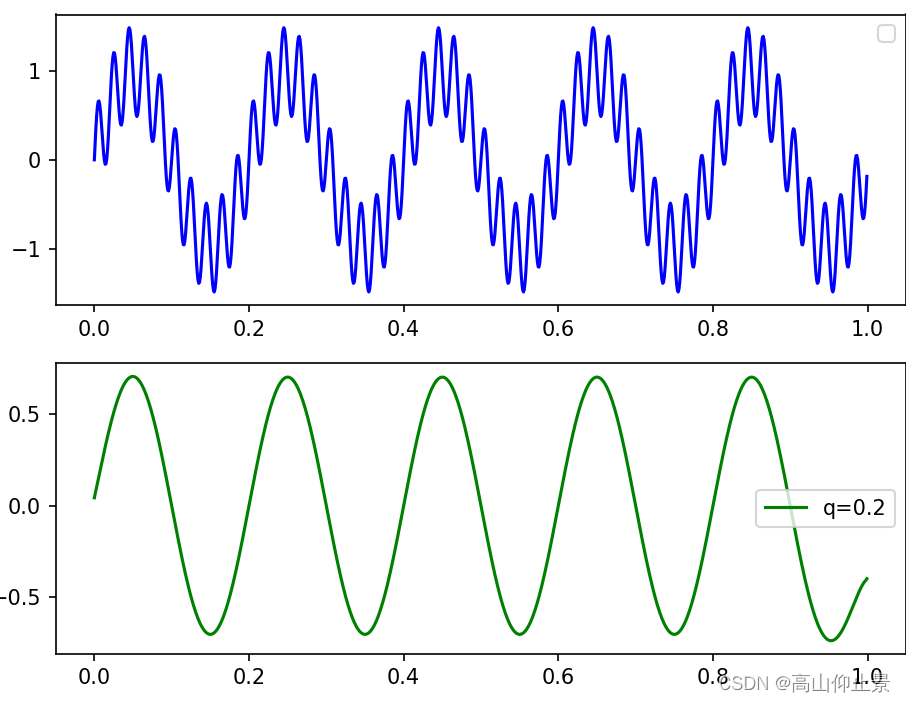
【Python 算法】信号处理通过陷波滤波器准确去除工频干扰
对于一个信号来说通常汇入工频噪声往往是因为交流电产生的电泳,影响了我们信号采集导致信号上存在工频干扰。 那么matlab去除工频干扰可以通过陷波滤波器实现。 通常使用scipy.signal实现信号的处理。 Scipy的信号处理模块(scipy.signal)来创…...

Redis(08)| 线程模型
一、redis 的线程模型 redis 内部使用文件事件处理器 file event handler,它是单线程的,所以redis才叫做单线程模型。它采用IO多路复用机制同时监听多个 socket,将产生事件的 socket 压入内存队列中,事件分派器根据 socket 上的事…...

Java14-16新特性
目录 一、Java14新特性 1、instanceof模式匹配 2、友好的空指针(NullPointerException)提示 3、record类型 二、Java15新特性 1、Sealed Classes 2、CharSequence新增方法 3、TreeMap新增方法 4、文本块 5、无需配置环境变量 三、Java16新特性 1、包装类构造方法的…...

中兴再推爆款,双2.5G网口的巡天AX3000Pro+仅需299元
10月30日消息,中兴新款路由器中兴巡天AX3000Pro将于10月31日20:00正式开售,当前可在天猫、京东及红魔商城进行预约,首发价格299元。 据了解,中兴巡天AX3000Pro是中兴智慧家庭推出的巡天系列新品,也是当前市场上唯一一款300元价位内配备双2.5G网口的路由器。 中兴巡天AX3000Pro…...

【系统架构】架构风格专题
目录 1、定义 2、通用架构风格分类 3、架构风格比较 4、示例:管道-过滤 VS 数据仓库)比较因素分析 1、定义 架构风格:描述某一特定应用领域中系统组织方式的惯用模式,反映了领域中众多系统所共有的结构和语义特性,…...

【Qt】盒子布局、网格布局、表单布局和堆栈布局
盒子布局 QBoxLayout可以在水平方向或垂直方向上排列控件,分别派生了QHBoxLayout、QVBoxLayout子类。 QHBoxLayout:水平布局,在水平方向上排列控件,即:左右排列。QVBoxLayout:垂直布局,在垂直…...

GO语言,半自动打怪
仅供学习参考,切勿用于商业用途 package mainimport ("fmt""github.com/go-vgo/robotgo""math/rand""time" )const (taskNum 7 )type Task struct {Name stringSleepTime1 intSleepTime2 intFunc func() }fu…...

【Java 进阶篇】Java登录案例详解
登录是Web应用程序中常见的功能,它允许用户提供凭证(通常是用户名和密码)以验证其身份。本文将详细介绍如何使用Java创建一个简单的登录功能,并解释登录的工作原理。我们将覆盖以下内容: 登录的基本概念创建一个简单的…...
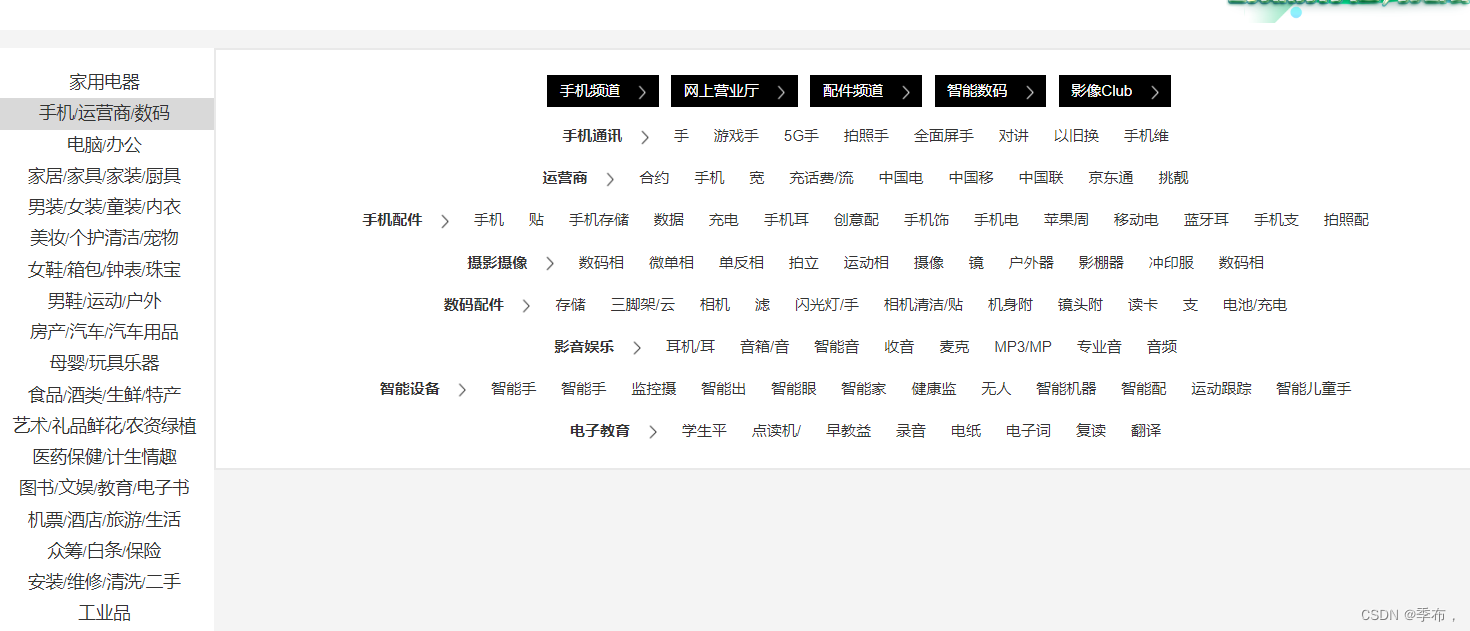
Vue 菜单导航栏,轮播图
导航菜单栏结构和样式代码实现 一级导航栏 views/HomeView.vue <template><div><Shortcut></Shortcut><Header></Header><div class"inner"><Navigation></Navigation></div><div>我是主页&l…...
讲述为什么要学习Adobe XD以及 Adobe XD下载安装
首先 我们要了解 Adobe XD 是个什么东西 XD是Adobe公司专门开发出来面向交互、界面设计的矢量绘图工具。 然后是 他可以做什么? 最基本的 可以做UI界面设置 所有 手机 平板 电脑等设备的UI界面 我们都可以通过XD完成 还有就是原型设置 我们可以做各种界面图 还有…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
