人大与加拿大女王大学金融硕士—与您共创辉煌
生活的本质就是有意识的活着,而生活的智慧就是活出了自己想要的样子,那些真正厉害的人,从来都在默默努力,伴随着金融人才的需求日益增长,中国人民大学与加拿大女王大学联合推出了人大女王金融硕士项目,旨在培养具有国际视野、专业素养和创新能力的金融精英。V13146152701
加拿大女王大学(Queen’s University)依照维多利亚女王的皇家宪章于1841年建立,被公认为是加拿大顶尖学府之一,对加拿大的高等教育影响深远。女王大学与麦吉尔大学、多伦多大学共称“加拿大常春藤盟校”。女王大学在加拿大联邦政府以及政商两界有着广泛的校友网络。在Globe and Mail (《环球邮报》、加拿大第二大日报)公布的大学排名中,女王大学获得学校口碑第一、职业口碑第一、学生满意度第一、建筑与设施第一。女王大学史密斯商学院(Smith School of Business)受到世界级评级机构的认可,其中包括美国的AACSB和欧洲的EQUIS体系。史密斯商学院与美国康奈尔大学联合举办的EMBA课程也取得了学术和行业内成功。自2010年起,女王大学史密斯商学院秉承高质量的办学风格在多伦多的“华尔街”Bay Street上开设金融硕士项目课程。该项目的低录取比例与优良的课程配置使之成为加拿大最热门的金融硕士项目。
中国人民大学(Renmin University of China,RUC)是国家人文社会学科的领头雁。在教育部学位评估中心2016年初公布的新一轮学科评估结果中,人民大学的金融学、理论经济学、应用经济学等九个学科排名全国第一,在人文社会科学领域位居全国高校之首。财政金融学院始建于1950年,其前身财政信用系是中国人民大学最早设立的八大院系之一,也是新中国第一个培养财政金融领域高级人才的基地,为新中国财政金融学科的建立和发展作出了开拓性贡献。经过50年的发展,财政金融学院在财政金融宏观理论和政策研究方面一直走在全国前列。随着社会主义市场经济的不断完善和财政金融制度改革的不断深化,财政金融学科不断向微观领域发展。21世纪初,财政金融学院的财政、金融两大学科均为国家重点学科。在教育部组织的1988年、2001年、2006年三次全国重点学科评审中,中国人民大学财政学、金融学均被评为全国重点学科,其中金融学科三次蝉联第一。这两大学科共包含财政学、税务、金融学、保险学、金融工程、信用管理六大专业。
人大女王金融硕士项目依托中加金融教育领域的两大顶尖学府,汇聚了优秀的师资、设计了科学的课程体系,每一位老师都有自己独特的教学方式,“理论讲授+案例分析+小组讨论+案例分享”是课程总体特色。老师们通过讲授国内外一些经典商业实战案例,将金融理论知识与实践进行整合,这其中尤其精彩的是王炜老师亲自撰写的哈佛商学院金融案例,线索错综复杂且逻辑严密。小组讨论时,往往需要反复阅读案例,结合老师讲授的理论知识并广泛查阅资料才能形成思路,然后建立分析模型,形成结论和报告,这其中自然免不了小组内部的激烈讨论。案例的分享也是很有意义的环节,各个小组分别展示自己的成果,老师逐个点评,不仅强化了对知识的理解,也增强了同学们之间的了解。整个过程下来,学生自主学习和教学参与感很强,仿佛自己就置身于一场场企业并购重组案之中。
那么人大女王金融硕士项目自身的优势也很多:
- 免联考、学制短、时间安排合理
人大与加拿大女王大学金融硕士项目不需要参加全国联考。金融硕士项目共设十门专业课程,每门课程3学分,共计30学分。学制共一年,每月两个周末授课(周六至周日),让工作、提升学历和学习同时进行。
- 独特教学方式
人大与加拿大女王大学金融硕士项目依托中加金融教育领域的两大顶尖学府,汇聚了优秀的师资、设计了科学的课程体系,每一位老师都有自己独特的教学方式,“理论讲授+案例分析+小组讨论+案例分享”是课程总体特色。通过国内外一些著名商业真实案例的讲授,将金融理论知识与学员实际体验相结合,注重理论与实践的整合,既了解国内金融的实际情况,又有深厚的国际背景,在课程的讲授上,更能基于国内金融行业状况有针对性的与国际金融先进经验进行引导、衔接、过渡。
- 高端人才汇聚
人大与加拿大女王大学金融硕士项目的学员都是来自金融领域各个行业的精英人员,课下会组织很多丰富多彩的活动,增长见识,结交许多新朋友。组织移动课堂活动走进澳门大学开展学习交流,参加高规格的经济论坛;探讨学术问题,交流工作经验,加深同学之间的情谊;组织大家参观北京金融资产交易所和腾讯集团,与行业内的资深人士面对面进行交流,除此之外,中国人民大学和女王史密斯商学院校友会也会组织一些精彩纷呈的活动,让项目在读同学与各届校友交流互动,建立起深厚的友谊。一年的共同学习时光,这份宝贵情谊,也将伴随你的终生。
- 可中留服学历学位认证
对于目前报考人大与加拿大女王大学金融硕士项目,无需出国即可拿到已有120年建校历史、职业口碑高居加拿大国内的女王大学金融硕士学位证书,证书可在中国教育部留学服务中心做学历学位认证。不仅省去了很大一笔费用,还能够为我们的职业生涯提供助力。
对于目前报考人大与加拿大女王大学金融硕士项目,无需出国即可拿到已有120年建校历史、职业口碑高居加拿大国内的女王大学金融硕士学位证书,证书可在中国教育部留学服务中心做学历学位认证。不仅省去了很大一笔费用,还能够为我们的职业生涯提供助力。我相信,通过在人大与加拿大女王大学金融硕士项目的学习,你将具备前沿的金融知识和技能。在这个日新月异、竞争激烈的时代,选择人大女王项目,就是选择一个充满无限可能的未来。我们期待着您的加入!
相关文章:

人大与加拿大女王大学金融硕士—与您共创辉煌
生活的本质就是有意识的活着,而生活的智慧就是活出了自己想要的样子,那些真正厉害的人,从来都在默默努力,伴随着金融人才的需求日益增长,中国人民大学与加拿大女王大学联合推出了人大女王金融硕士项目,旨在…...
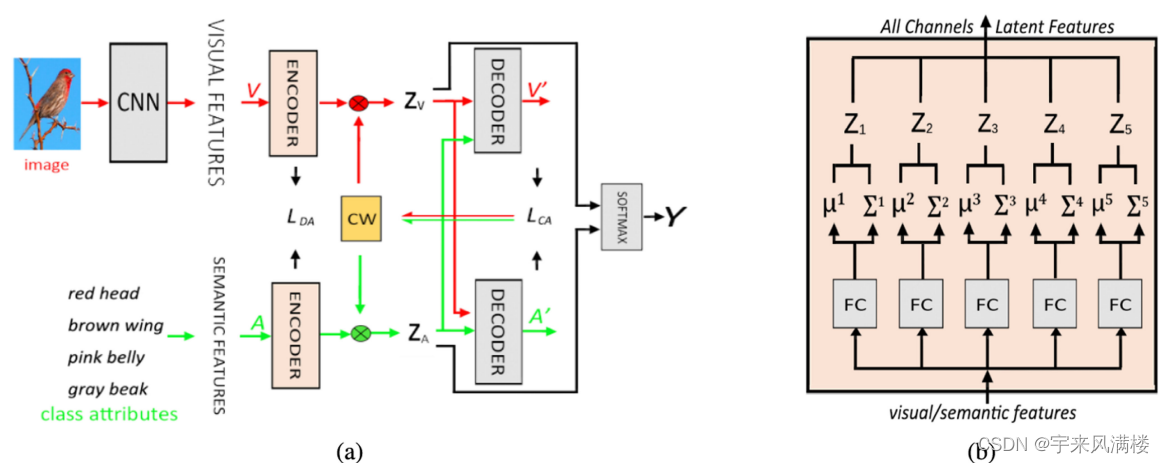
Generalized Zero-Shot Learning With Multi-Channel Gaussian Mixture VAE
L D A _{DA} DA最大化编码后两种特征分布之间的相似性 辅助信息 作者未提供代码...
)
10.30 知识总结(标签分类、css介绍等)
一、 标签的分类 1.1 单标签 img br hr <img /> 1.2 双标签 a h p div <a></a> 1.3 按照标签属性分类 1.3.1 块儿标签 即自己独自占一行 h1-h6 p div 1.3.2 行内(内联)标签 即自身文本有多大就占多大 a span u i b s 二、 标签的嵌套 标签之间是可以互相…...
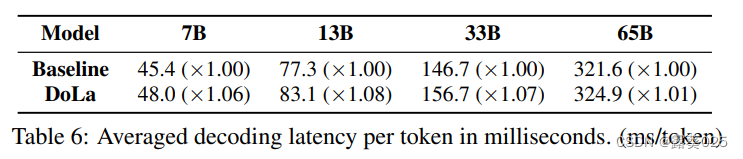
DoLa:对比层解码提高大型语言模型的事实性
DoLa:对比层解码提高大型语言模型的事实性 摘要1 引言2 方法2.1 事实知识在不同层级上演化2.2 动态早期层选择2.3 预测对比 3 实验3.1 任务3.2 实验设置3.3 多项选择3.3.1 TruthfulQA:多项选择3.3.2 FACTOR:维基、新闻 3.4 开放式文本生成3.4…...

解决由于找不到mfc140u.dll无法继续执行此代码问题的4个方法
mfc140u.dll是Microsoft Foundation Class(微软基础类库)中的一个动态链接库文件,它包含了许多用于实现Windows应用程序的基本功能。当我们在编写或运行基于MFC的程序时,如果系统中缺少这个文件,就会出现“找不到mfc14…...

MySQL高性能优化规范建议
当涉及到MySQL数据库的性能优化时,有许多方面需要考虑。以下是一些通用的MySQL性能优化规范建议: 合适的索引: 确保表中的字段使用了适当的索引。这能大幅提升检索速度。但避免过多索引,因为它会增加写操作的成本。 优化查询语句…...
pytorch 入门 (五)案例三:乳腺癌识别-VGG16实现
本文为🔗小白入门Pytorch内部限免文章 🍨 本文为🔗小白入门Pytorch中的学习记录博客🍦 参考文章:【小白入门Pytorch】乳腺癌识别🍖 原作者:K同学啊 在本案例中,我将带大家探索一下深…...

vue中electron与vue通信(fs.existsSync is not a function解决方案)
electron向vue发送消息 dist/main.js (整个文件配置在另一条博客里) win new BrowserWindow({width:1920,height:1080,webPreferences: {// 是否启用Node integrationnodeIntegration: true, // Electron 5.0.0 版本之后它将被默认false// 是否在独立 JavaScript 环境中运行…...

LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks翻译
论文《LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks》翻译 LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks翻译...

文件类漏洞总结, 文件包含, 文件上传, 文件下载
文件类漏洞总结 一, 文件包含 1. 文件包含绕过 实际环境中不是都是像$_GET[file]; incude $file 这样直接把变量传入包含函数的。 在很多时候包含的变量文件不是完全可控的,比如下面这段代码指定了前缀和后缀: <?php $file S_GET[filename]; include /opt/…...

SpringBoot篇---第四篇
系列文章目录 文章目录 系列文章目录一、springboot常用的starter有哪些二、 SpringBoot 实现热部署有哪几种方式?三、如何理解 Spring Boot 配置加载顺序? 一、springboot常用的starter有哪些 spring-boot-starter-web 嵌入tomcat和web开发需要servlet…...
 -- 在不同版本SpringBoot,选用不同的Knife4j相关的jar包)
Knife4j使用教程(一) -- 在不同版本SpringBoot,选用不同的Knife4j相关的jar包
目录 1. Knife4j的项目背景 2. Knife4j的选择 2.1 选用 Spring Boot 版本在 2.4.0~3.0.0之间 2.2 选用 Spring Boot 版本在 3.0.0之上...
Octave Convolution学习笔记 (附代码)
论文地址:https://export.arxiv.org/pdf/1904.05049 代码地址:https://gitcode.com/mirrors/lxtgh/octaveconv_pytorch/overview?utm_sourcecsdn_github_accelerator 1.是什么? OctaveNet网络属于paper《Drop an Octave: Reducing Spatia…...
SpringSecurity 认证实战
一. 项目数据准备 1.1 添加依赖 <dependencies><!--spring security--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-security</artifactId></dependency><!--web起步依赖-…...
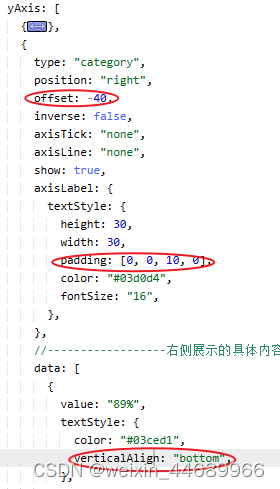
echarts中横向柱状图的数字在条纹上方
实现效果: 数字在条纹的上方 实现方法:这些数字是用新添加一个坐标轴来实现的 直接添加坐标轴数字显示是在条纹的正右边 所以需要配置一下偏移 完整代码 var option {grid: {left: "3%",right: "4%",bottom: "3%",cont…...

【仙逆】尸阴宗始祖现身,王林修得黄泉生窍诀,阿呆惊险逃生
【侵权联系删除】【文/郑尔巴金】 深度爆料最新集,王林终于成功筑基,这一集的《仙逆》动漫真是让人热血沸腾啊!在这个阶段,王林展现出了他的决心和毅力,成功地击杀了藤厉,并采取了夺基大法,从藤…...

C++二叉树剪枝
文章目录 C二叉树剪枝题目链接题目描述解题思路代码复杂度分析 C二叉树剪枝 题目链接 LCR 047. 二叉树剪枝 - 力扣(LeetCode) 题目描述 给定一个二叉树 根节点 root ,树的每个节点的值要么是 0,要么是 1。请剪除该二叉树中所有节…...
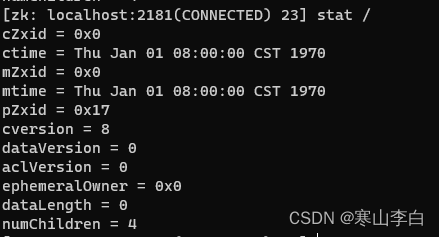
ZooKeeper中节点的操作命令(查看、创建、删除节点)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...
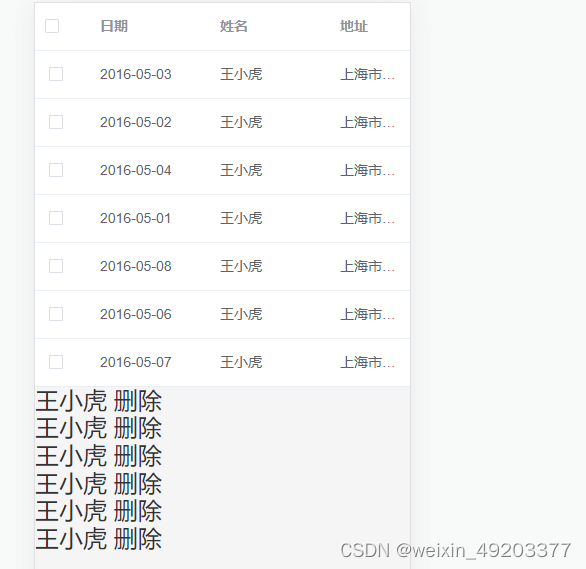
el-table多选表格 实现默认选中 删除选中列表取消勾选等联动效果
实现效果如下: 代码如下: <template><div><el-tableref"multipleTable":data"tableData"tooltip-effect"dark"style"width: 100%"selection-change"handleSelectionChange"><…...
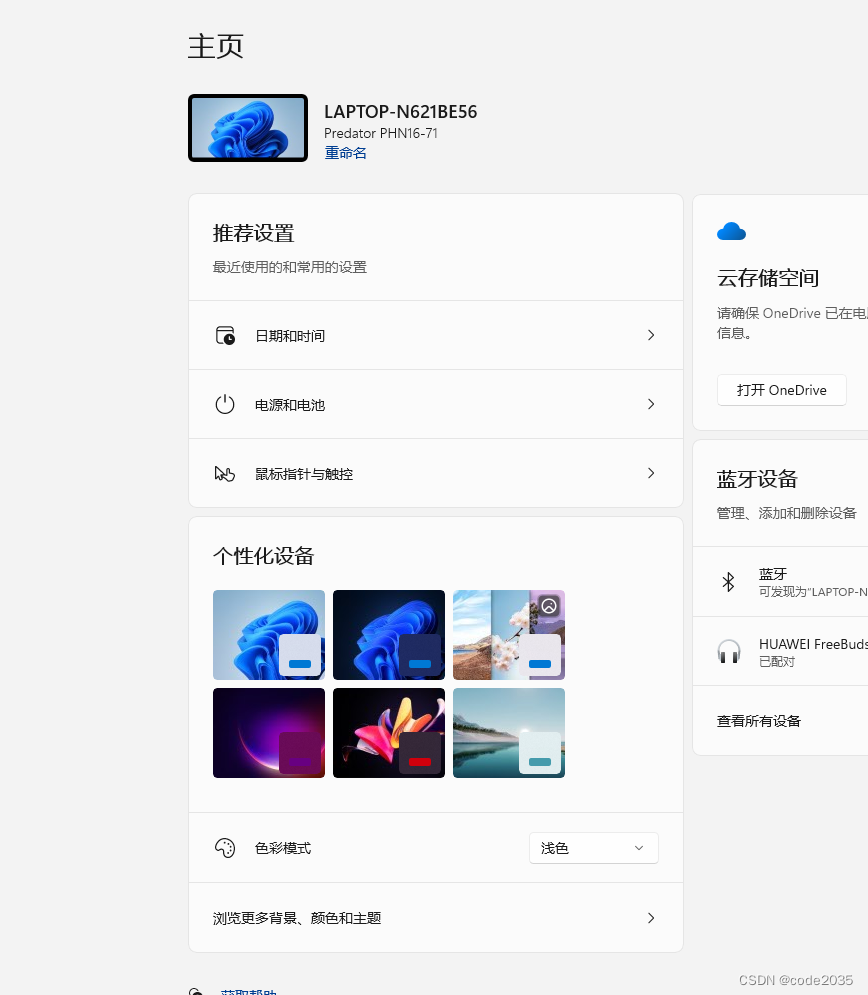
预安装win11的电脑怎么退回正版win10?
对于新购的笔记本 通常来讲预装的系统是全新安装的,是没有之前Windows10系统文件的,无法回退。 可以打开设置-----系统----恢复-----看下是否有该选项。 ------------------------------------------------------------------------------- 若是在上述…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
