0-1背包问题【穷举法+二维dp数组】
问题描述:
使用穷举法解决0/1背包问题。问题描述:给定n个重量为{w1, w2, … ,wn}、价值为{v1, v2, … ,vn}
的物品和一个容量为C的背包,求这些物品中的一个最有价值的子集,且要能够装到背包中。
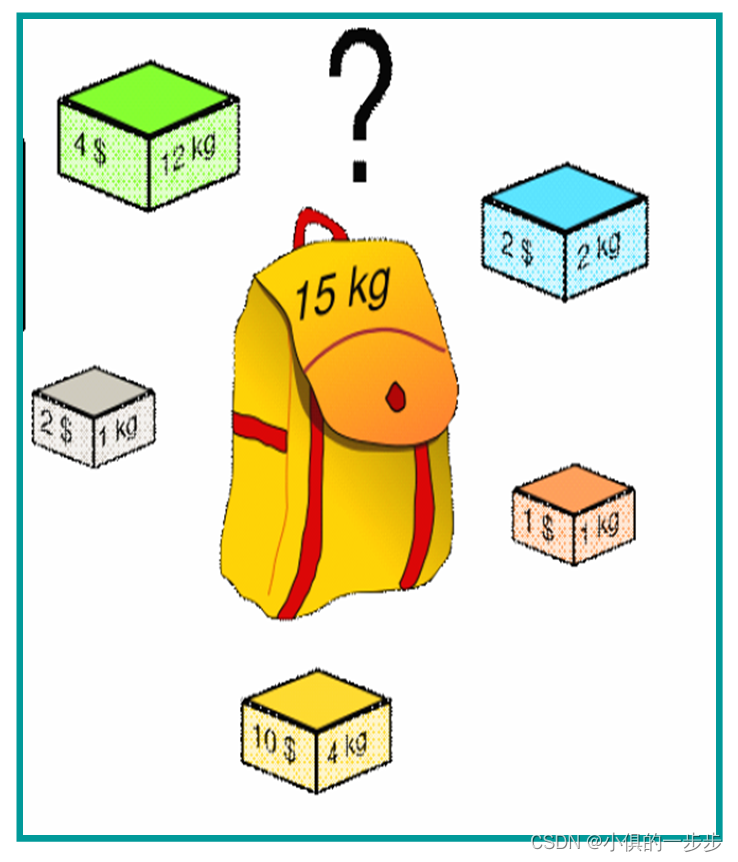
穷举法:每件物品装还是不装有两种选择,使用0-表示不装,1表示装,n件物品就有2^n种,穷举2^n种,找到符合符合weight背包容量的且为价值最大的方式。
public class Main01 {//穷举法public void pack01(int weight,int[] wt,int[] val){int n = wt.length;int count= (int) Math.pow(2,n);int maxVal = 0;//枚举32种情况,并且记录符合weight重量背包的最大价值for (int i = 0; i < count; i++) {String res = String.format("%5s",Integer.toBinaryString(i)).replace(' ','0');System.out.print(res+" ");int sumVal = 0;int sumWeight=0;for (int j = 0; j < n; j++) {//为1时表示装该物品 0表示不准装if (res.charAt(j)=='1') {sumVal += val[j];sumWeight += wt[j];}if (sumWeight<=weight){maxVal = Math.max(sumVal,maxVal);}}System.out.println("价值:"+sumVal+"重量:"+sumWeight);}//打印最大价值下对应的背包实际重量和所装物品的状态for (int i = 0; i<count; i++) {String res = String.format("%5s",Integer.toBinaryString(i)).replace(' ','0');int sumVal = 0;int sumWeight=0;for (int j = 0; j < n; j++) {if (res.charAt(j)=='1') {sumVal += val[j];sumWeight += wt[j];}}if (sumVal==maxVal&&sumWeight<=weight){System.out.println("当背包重量为"+weight+"时:最大价值:"+sumVal+" 总重量: "+sumWeight+" 方式:"+res);break;}}}public static void main(String[] args) {Main01 main01 = new Main01();int[] wt = {1, 2, 1, 12, 4};int[] val = {1, 2, 2, 4, 10};main01.pack01(15, wt, val);}
}输出结果:
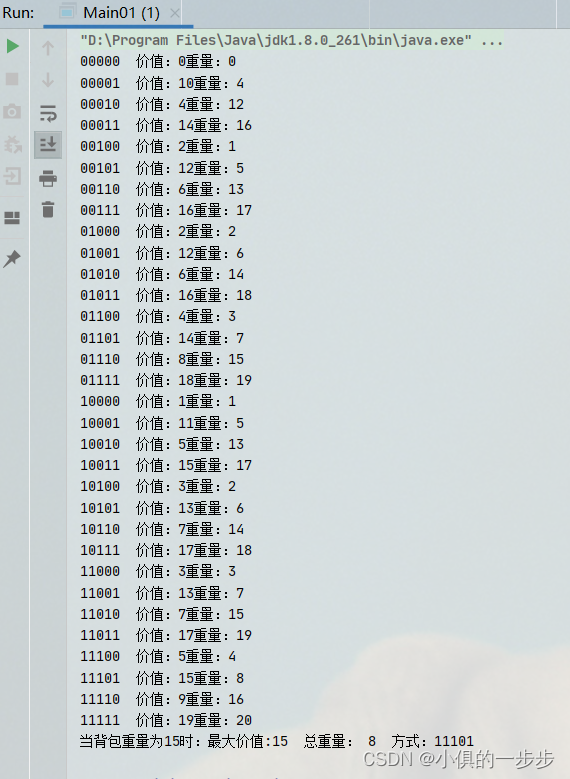
二维dp数组:
dp[i][w]数组含义:对于前i个物品,当前背包容量为w时,可装下的最大值是dp[i][w]。
dp[i-1][w-wt[i-1]]+val[i-1]:装物品i的价值
dp[i-1][w]:不装物品i的价值
因此dp[i][w]取装物品 i dp[i-1][w-wt[i-1]]+val[i-1] 和 不装物品i dp[i-1][w] 的最大值
public class Main01 {public static void main(String[] args) {int[] wt = {1, 2, 1, 12, 4};int[] val = {1, 2, 2, 4, 10};int res = pack01(15,wt,val);System.out.println("最大价值:"+res);}public static int pack01(int weight,int[] wt,int[] val){int n = wt.length;//dp[i][w]数组含义:对于前i个物品,当前背包容量为w时,可装下的最大值是dp[i][w]int[][] dp = new int[n+1][weight+1];for (int i = 1; i <= n; i++) {for (int w = 1; w <= weight; w++) {if (wt[i-1]>w){//不能装入背包dp[i][w] = dp[i-1][w];}else {//择优装入背包dp[i][w] = Math.max(dp[i-1][w-wt[i-1]]+val[i-1],dp[i-1][w]);}}}//打印dp表for (int i = 0; i <=n ; i++) {for (int j = 0; j <=weight ; j++) {if (j<weight){System.out.print(dp[i][j]+",");}else {System.out.print(dp[i][j]);}}System.out.println();}return dp[n][weight];}
}
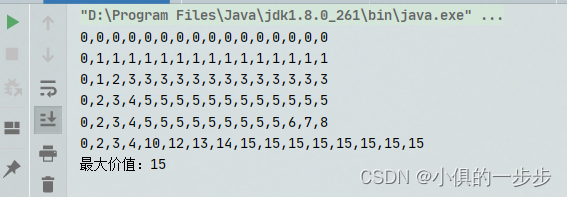
输出结果:
相关文章:

0-1背包问题【穷举法+二维dp数组】
问题描述: 使用穷举法解决0/1背包问题。问题描述:给定n个重量为{w1, w2, … ,wn}、价值为{v1, v2, … ,vn} 的物品和一个容量为C的背包,求这些物品中的一个最有价值的子集,且要能够装到背包中。 穷举法:每件物品装还是…...
nodejs+vue+python+php基于微信小程序的在线学习平台设计与实现-计算机毕业设计
困扰管理层的许多问题当中,在线学习也是不敢忽视的一块。但是管理好在线学习又面临很多麻烦需要解决,例如:如何在工作琐碎,记录繁多的情况下将在线学习的当前情况反应给课程问题管理员决策,等等。 流,开发一个在线学习平台小程序一方面的可能会更合乎时宜,另一方面来…...
Spring学习笔记2 Spring的入门程序
Spring学习笔记1 启示录_biubiubiu0706的博客-CSDN博客 Spring官网地址:https://spring.io 进入github往下拉 用maven引入spring-context依赖 写spring的第一个程序 引入下面依赖,好比引入Spring的基本依赖 <dependency><groupId>org.springframework</groupId&…...
)
【Linux】虚拟机安装Linux、客户端工具及Linux常用命令(详细教程)
一、导言 1、引言 Linux是一个开源的操作系统内核,它最初由芬兰计算机科学家Linus Torvalds于1991年开发。Linux不同于传统的商业操作系统,它常用于服务器、嵌入式系统和个人电脑等各种平台。 Linux具有很多优点,包括稳定性、安全性和可定制…...

Day 47 动态规划 part13
Day 47 动态规划 part13 解题理解300674718 3道题目 300. 最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组 解题理解 300 dp[i]被设置为以nums[i]为结尾的最长递增子序列长度。 class Solution:def lengthOfLIS(self, nums: List[int]) -> int:if len(nums) …...

【广州华锐互动】飞机诊断AR远程指导系统为工程师提供更多支持
随着科技的发展,飞机的维护工作也在不断进步。其中,AR(增强现实)技术的应用使得远程运维成为可能。本文将探讨AR在飞机诊断远程指导系统中的应用,以及它对未来航空维护模式的影响。 AR远程指导系统是一种使用增强现实技…...
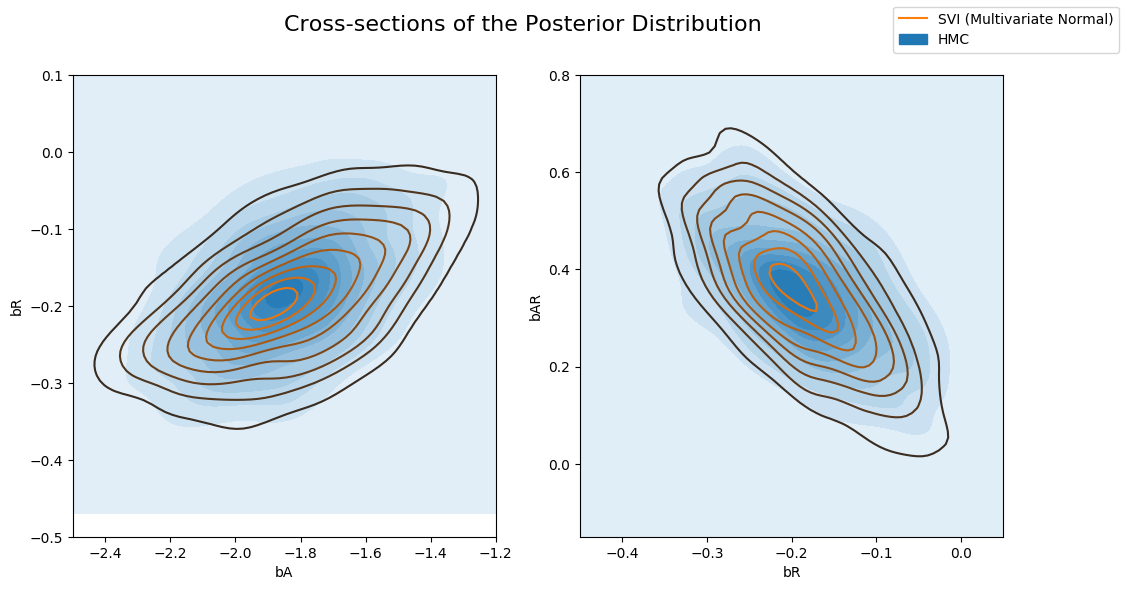
【贝叶斯回归】【第 2 部分】--推理算法
一、说明 在第一部分中,我们研究了如何使用 SVI 对简单的贝叶斯线性回归模型进行推理。在本教程中,我们将探索更具表现力的指南以及精确的推理技术。我们将使用与之前相同的数据集。 二、模块导入 [1]:%reset -sf[2]:import logging import osimport tor…...

【深入浅出汇编语言】寄存器精讲第二期
🌈个人主页:聆风吟 🔥系列专栏:数据结构、算法模板、汇编语言 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️物理地址二. ⛳️16位结构的CPU三. ⛳️8086CPU给出物理地址的方…...

如何保证分布式情况下的幂等性
关于这个分布式服务的幂等性,这是在使用分布式服务的时候会经常遇到的问题,比如,重复提交的问题。而幂等性,就是为了解决问题存在的一个概念了。 什么是幂等 幂等(idempotent、idempotence)是⼀个数学与计算机学概念,常⻅于抽象代数中。 在编程中⼀个幂等操作的特点是…...

Mybatis特殊SQL的执行
文章目录 模糊查询批量删除动态设置表名添加功能获取自增的主键自定义映射resultMapresultMap处理字段和属性的映射关系 多对一映射处理级联方式处理映射关系使用association处理映射关系 分步查询1. 查询员工信息 2. 查询部门信息 一对多映射处理collection 模糊查询 /*** 根…...
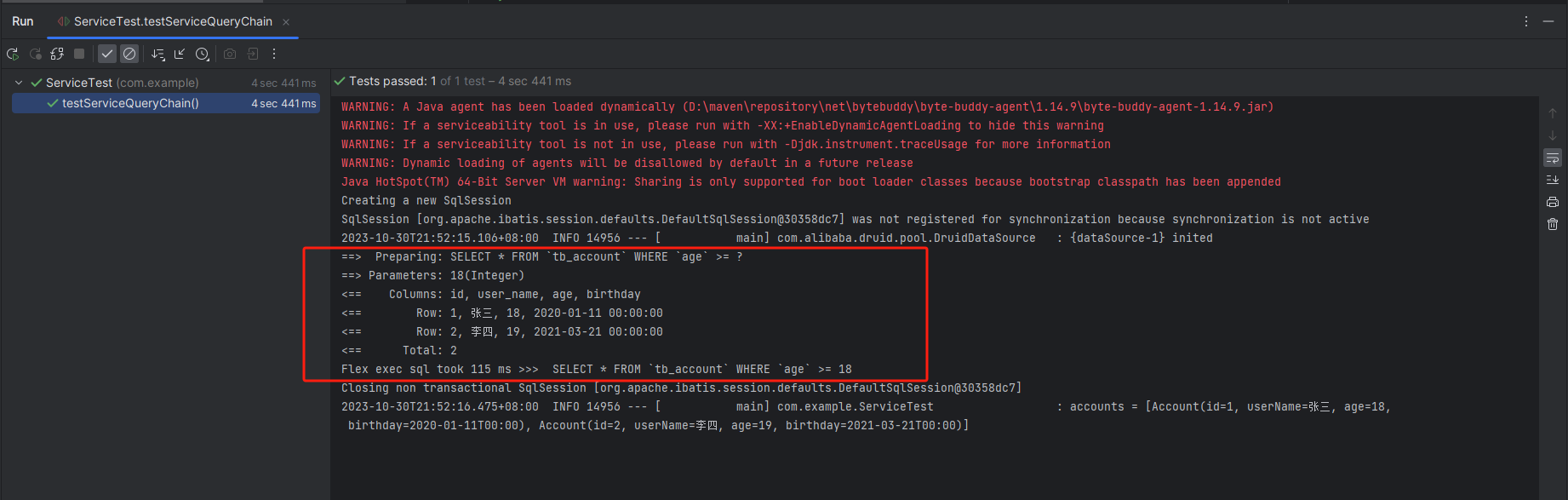
MyBatis-Flex(一):快速开始
框架介绍 MyBatis-Flex 是一个优雅的 MyBatis 增强框架,它非常轻量、同时拥有极高的性能与灵活性。 MyBatis-Flex 官方文档 说明 本文参照官方文档的【快速开始】 章节,编写 Spring Boot 项目的代码示例。 快速开始 创建数据库表 直接参照官网示…...

Vue组件化
组件 组件是实现应用中局部功能的代码(HTML,CSS,JS)和资源(图片,声音,视频)的集合,凡是采用组件方式开发的应用都可以称为组件化应用 模块是指将一个大的js文件按照模块化拆分规则进行拆分成的每个js文件, 凡是采用模块方式开发的应用都可以称为模块化应用(组件包括模块) 传…...

nodejs+python+php+微信小程序-基于安卓android的健身服务应用APP-计算机毕业设计
考虑到实际生活中在健身服务应用方面的需要以及对该系统认真的分析,将系统权限按管理员和用户这两类涉及用户划分。 则对于进一步提高健身服务应用发展,丰富健身服务应用经验能起到不少的促进作用。 健身服务应用APP能够通过互联网得到广泛的、全面的宣…...
SpringCloud 微服务全栈体系(九)
第九章 Docker 三、Dockerfile 自定义镜像 常见的镜像在 DockerHub 就能找到,但是我们自己写的项目就必须自己构建镜像了。 而要自定义镜像,就必须先了解镜像的结构才行。 1. 镜像结构 镜像是将应用程序及其需要的系统函数库、环境、配置、依赖打包而…...
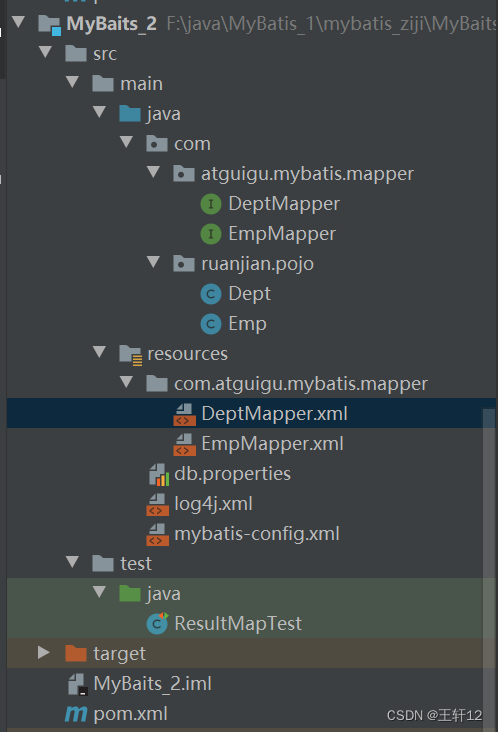
Mybatis 多对一和一对多查询
文章目录 Mybatis 多对一 and 一对多查询详解数据库需求Mybatis代码注意 Mybatis 多对一 and 一对多查询详解 数据库 员工表 t_emp 部门表 t_dept CREATE TABLE t_emp (emp_id int NOT NULL AUTO_INCREMENT,emp_name varchar(25) CHARACTER SET utf8 COLLATE utf8_general_ci…...
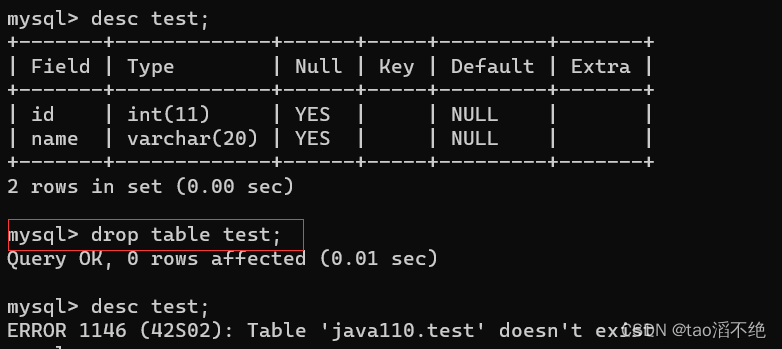
MySQL的数据库操作、数据类型、表操作
目录 一、数据库操作 (1)、显示数据库 (2)、创建数据库 (3)、删除数据库 (4)、使用数据库 二、常用数据类型 (1)、数值类型 (2࿰…...

音视频技术开发周刊 | 317
每周一期,纵览音视频技术领域的干货。 新闻投稿:contributelivevideostack.com。 MIT惊人再证大语言模型是世界模型!LLM能分清真理和谎言,还能被人类洗脑 MIT等学者的「世界模型」第二弹来了!这次,他们证明…...

【JavaSE专栏58】“Java构造函数:作用、类型、调用顺序和最佳实践“ ⚙️⏱️
解析Java构造函数:作用、类型、调用顺序和最佳实践" 🚀📚🔍🤔📝🔄⚙️⏱️📖🌐 摘要引言1. 什么是构造函数 🤔2. 构造函数的类型与用途 📝1.…...
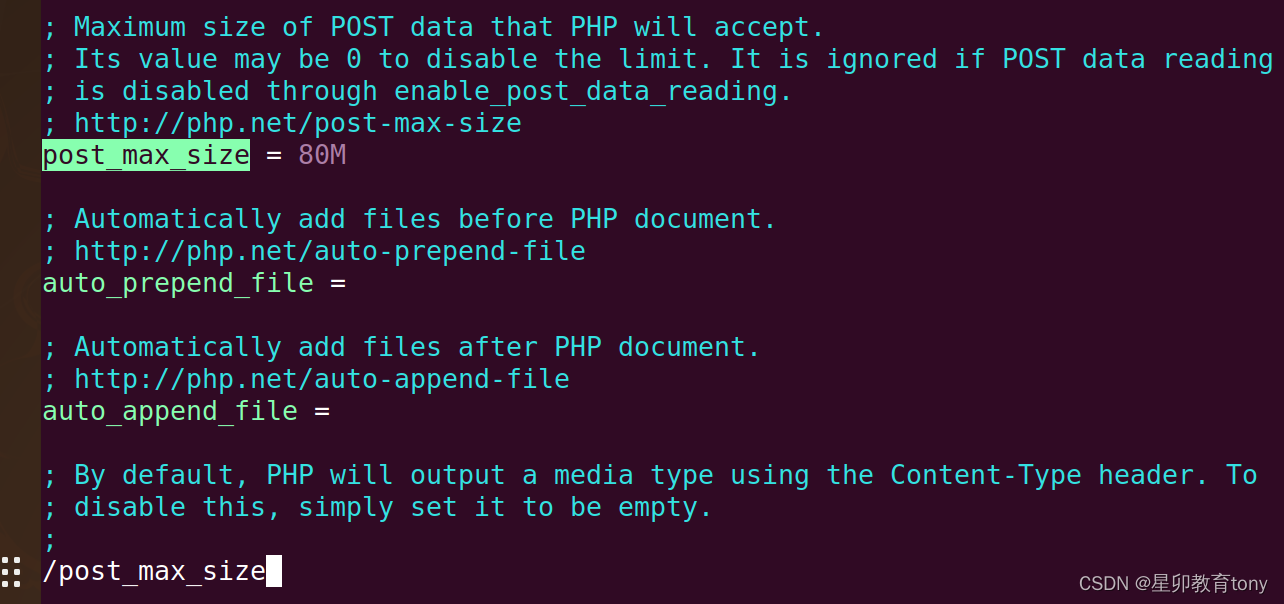
Ubuntu系统HUSTOJ 用 vim 修改php.ini 重启PHP服务
cd / sudo find -name php.ini 输出: ./etc/php/7.4/cli/php.ini ./etc/php/7.4/fpm/php.ini sudo vim /etc/php/7.4/cli/php.ini sudo vim /etc/php/7.4/fpm/php.ini 知识准备: vim的搜索与替换 在正常模式下键入 / ,即可进入搜索模式…...

案例分析真题-信息安全
案例分析真题-信息安全 2009年真题 【问题1】 【问题2】 【问题3】 2010年真题 【问题1】 【问题2】 【问题3】 2011 年真题 【问题1】 【问题2】 【问题3】 骚戴理解:这个破题目完全考的知识储备,不知道的连手都动不了,没法分析 2013年真题…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
