力扣第509题 斐波那契数 新手动态规划(推荐参考) c++
题目
509. 斐波那契数
简单
相关标签
递归 记忆化搜索 数学 动态规划
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
思路和解题方法
在这段代码中,函数
fib接受一个整数N作为参数,返回斐波那契数列中第N个数的值。如果N小于等于1,则直接返回N。if (N <= 1) return N;接下来,我们使用动态规划的思想来求解斐波那契数列。我们定义一个一维数组
dp,其中dp[i]表示斐波那契数列中第i个数的值。我们先将数组的前两个元素初始化为0和1。vector<int> dp(N + 1); dp[0] = 0; dp[1] = 1;接下来,我们使用循环遍历数组中的每个元素,计算出当前位置的值。根据斐波那契数列的定义,第i个数的值应该等于前两个数的和,即
dp[i-1] + dp[i-2]。最后,返回数组中第N个数的值。for (int i = 2; i <= N; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[N];
复杂度
时间复杂度:
O(N)
时间复杂度是O(N),其中N是斐波那契数列中第N个数的值。在循环中,我们需要遍历数组中的每个元素一次,并且每次计算都需要使用前两个数的和,所以时间复杂度与N成正比。
空间复杂度
O(N)
空间复杂度也是O(N),因为我们需要使用一个数组来保存斐波那契数列中每个数的值。数组的长度为N+1,所以空间复杂度与N成正比。
c++ 代码
class Solution {
public:int fib(int N) {// 如果N小于等于1,则直接返回Nif (N <= 1) return N;// 创建一个大小为N+1的数组,用于保存斐波那契数列中每个数的值vector<int> dp(N + 1);// 初始化数组的前两个元素为0和1dp[0] = 0;dp[1] = 1;// 使用动态规划的思想计算斐波那契数列for (int i = 2; i <= N; i++) {// 当前位置的值等于前两个数的和dp[i] = dp[i - 1] + dp[i - 2];}// 返回斐波那契数列中第N个数的值return dp[N];}
};
常数空间代码
只是对于dp来维护两个数
class Solution {
public:int fib(int n) {// 如果n小于等于1,直接返回nif (n <= 1) return n;// 初始化斐波那契数列的前两个数int n1 = 0, n2 = 1;// 用于保存当前位置的值int ans = 0;// 从第3个位置开始遍历到第n个位置for (int i = 2; i <= n; i++) {// 计算当前位置的值,即前两个数的和ans = n1 + n2;// 更新前两个数的值n1 = n2;n2 = ans;}// 返回斐波那契数列中第n个数的值return ans;}
};
附上递归解法
class Solution {
public:int fib(int N) {if (N < 2) return N;return fib(N - 1) + fib(N - 2);}
};觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:
 c++)
力扣第509题 斐波那契数 新手动态规划(推荐参考) c++
题目 509. 斐波那契数 简单 相关标签 递归 记忆化搜索 数学 动态规划 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0&a…...

canvas绘制签名并保存
实现签名的三个关键方法: 1.mousedown:当鼠标按下时开始绘制签名。 2.mousemove:鼠标移动时持续绘制。 3.mouseup:鼠标抬起时结束绘制。 html: <div class"setSign"><canvasref"canvas&q…...
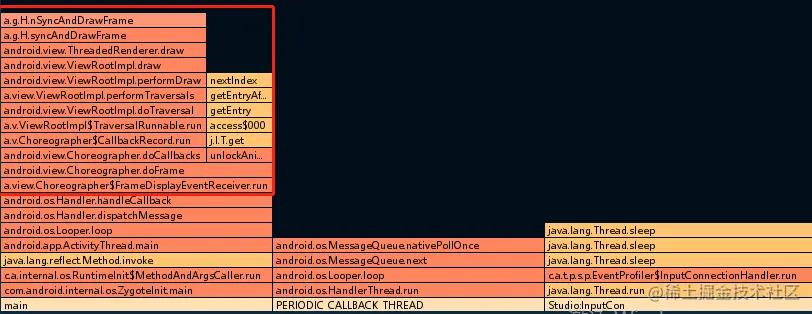
Android渲染流程
目录 缓冲区的不同生命周期代表当前缓冲区的状态: 多个源 ViewRootImpl: Android4.0: Android5.0: Android应用程序调用SurfaceFliger将测量,布局,绘制好的Surface借助GPU渲染显示到屏幕上。 一个Acti…...

牛客-【237题】算法基础精选题单-第二章 递归、分治
第二章 递归、分治 递归NC15173 The Biggest Water ProblemNC22164 更相减损术 递归 NC15173 The Biggest Water Problem 简单递归,直接暴力 #include <math.h> #include <stdio.h> #include <algorithm> #include <cstring> #include &…...

leetcode-字符串
1.反转字符串LeetCode344. 20230911 难度为0,此处就不放代码了 注意reverse和swap等一系列字符串函数什么时候该用,记一记库函数 swap可以有两种实现,涨知识了,除了temp存值还可以通过位运算:s[i] ^ s[j]; s[j] ^ s[i…...

多线程---synchronized特性+原理
文章目录 synchronized特性synchronized原理锁升级/锁膨胀锁消除锁粗化 synchronized特性 互斥 当某个线程执行到某个对象的synchronized中时,其他线程如果也执行到同一个对象的synchronized就会阻塞等待。 进入synchronized修饰的代码块相当于加锁 退出synchronize…...
Qt实现卡牌对对碰游戏
效果 闲来无事,实现一个对对碰游戏,卡牌样式是火影动漫。 先上效果: 卡牌对对碰_火影主题 玩法 启动游戏,进入第一关卡,所有卡牌都为未翻开状态,即背面朝上;点击卡牌,则将卡牌翻开…...

【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割7(数据预处理)
在上一节:【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割6(数据预处理) 中,我们已经得到了与mhd图像同seriesUID名称的mask nrrd数据文件了,可以说是一一对应了。 并且,mask的文件,还根据结…...

极米科技H6 Pro 4K、H6 4K高亮定焦版——开启家用投影4K普及时代
智能投影产业经过几年发展,市场规模正在快速扩大。洛图数据显示,预计今年中国投影出货量有望超700万台,2027年达950万台,可见智能投影产业规模将逐渐壮大,未来可期。2023年,投影行业呈现出全新面貌…...
软考系统架构师知识点集锦九:数据库系统
一、考情分析 二、考点精讲 2.1数据库概述 2.1.1数据库模式 (1)三级模式:外模式对应视图,模式(也称为概念模式)对应数据库表,内模式对应物理文件。(2)两层映像:外模式-模式映像,模式-内模式映像;两层映像可以保证数据库中的数据具有较高的…...

IOC课程整理-6 Spring IoC 依赖注入
1 依赖注入的模式和类型 模式 类型 2 自动绑定(Autowiring) 官方定义 “自动装配是Spring框架中一种机制,用于自动解析和满足bean之间的依赖关系。通过自动装配,Spring容器可以根据类型、名称或其他属性来自动连接协作的bean&…...
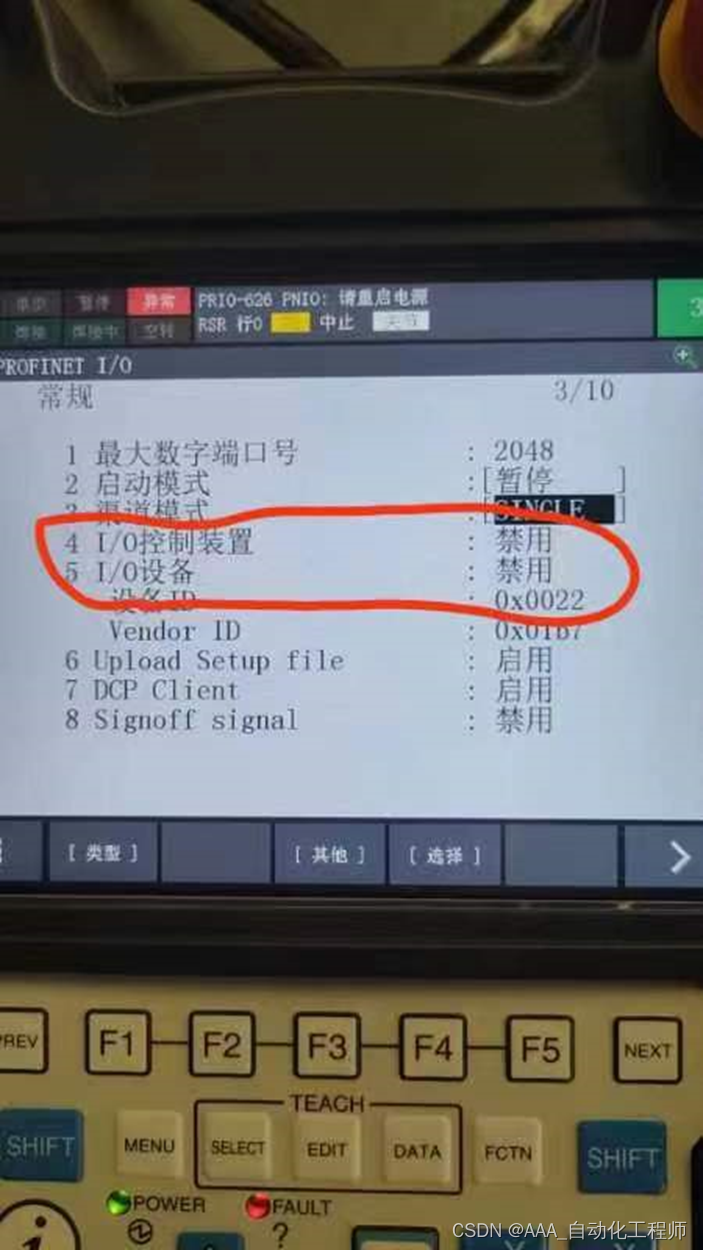
FANUC机器人PRIO-621和PRIO-622设备和控制器没有运行故障处理
FANUC机器人PRIO-621和PRIO-622设备和控制器没有运行故障处理 如下图所示,新的机器人开机后提示报警: PRIO-621 设备没有运行 PRIO-622 控制器没有运行 我们首先查看下手册上的报警代码说明,如下图所示, 如下图所示,…...
《动手深度学习》线性回归简洁实现实例
🎈 作者:Linux猿 🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C、云计算、物联网、面试、刷题、算法尽管咨询我,关注我,有问题私聊! &…...

国家数据局正式揭牌,数据专业融合型人才迎来发展良机
📕作者简介:热爱跑步的恒川,致力于C/C、Java、Python等多编程语言,热爱跑步,喜爱音乐的一位博主。 📗本文收录于恒川的日常汇报系列,大家有兴趣的可以看一看 📘相关专栏C语言初阶、C…...
基于springboot实现休闲娱乐代理售票平台系统项目【项目源码+论文说明】
基于springboot实现休闲娱乐代理售票系统演示 摘要 网络的广泛应用给生活带来了十分的便利。所以把休闲娱乐代理售票管理与现在网络相结合,利用java技术建设休闲娱乐代理售票系统,实现休闲娱乐代理售票的信息化。则对于进一步提高休闲娱乐代理售票管理发…...
)
3.AUTOSAR OS分析(一)
1. AUTOSAR OS诞生背景 在最初接触汽车ECU开发时,提到最多的还是OSEK,比如OSEK NM、OSEK OS等等;而OSEK/VDK操作系统也是最先引入汽车行业;OSEK OS是基于事件触发的操作系统,有以下特性: 固定优先级调度中断处理函数StartOS和StartupHook作为启动阶段的通用接口函数Shutd…...
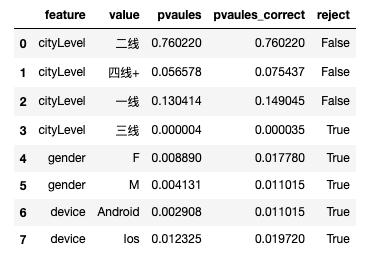
AB试验(七)利用Python模拟A/B试验
AB试验(七)利用Python模拟A/B试验 到现在,我相信大家理论已经掌握了,轮子也造好了。但有的人是不是总感觉还差点什么?没错,还缺了实战经验。对于AB实验平台完善的公司 ,这个经验不难获得&#…...

Go语言入门-流程控制语句
流程控制 Go语言中有以下几种常见的流程控制语句: 条件语句(Conditional Statements): if语句:用于根据条件执行代码块。else语句:在if条件不满足时执行的语句块。else if语句:用于在多个条件之…...

深入探究ASEMI肖特基二极管MBR60100PT的材质
编辑-Z 在电子零件领域中,肖特基二极管MBR60100PT因其出色的性能和广泛的应用而显得尤为关键。理解其材质不仅有助于我们深入理解其运作原理,也有助于我们做出更合适的电子设计。那么,肖特基二极管MBR60100PT是什么材质呢? 首先,…...

python类模拟“对战游戏”
Game类含玩家昵称、生命值、攻击力(整数),暴击率、闪避率(小数),在魔术方法init定义;attack方法中实现两个Game实例对战模拟。 (本笔记适合初通Python类class的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.py…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
