聚类算法(上):8个常见的无监督聚类方法介绍和比较
无监督聚类方法的评价指标必须依赖于数据和聚类结果的内在属性,例如聚类的紧凑性和分离性,与外部知识的一致性,以及同一算法不同运行结果的稳定性。
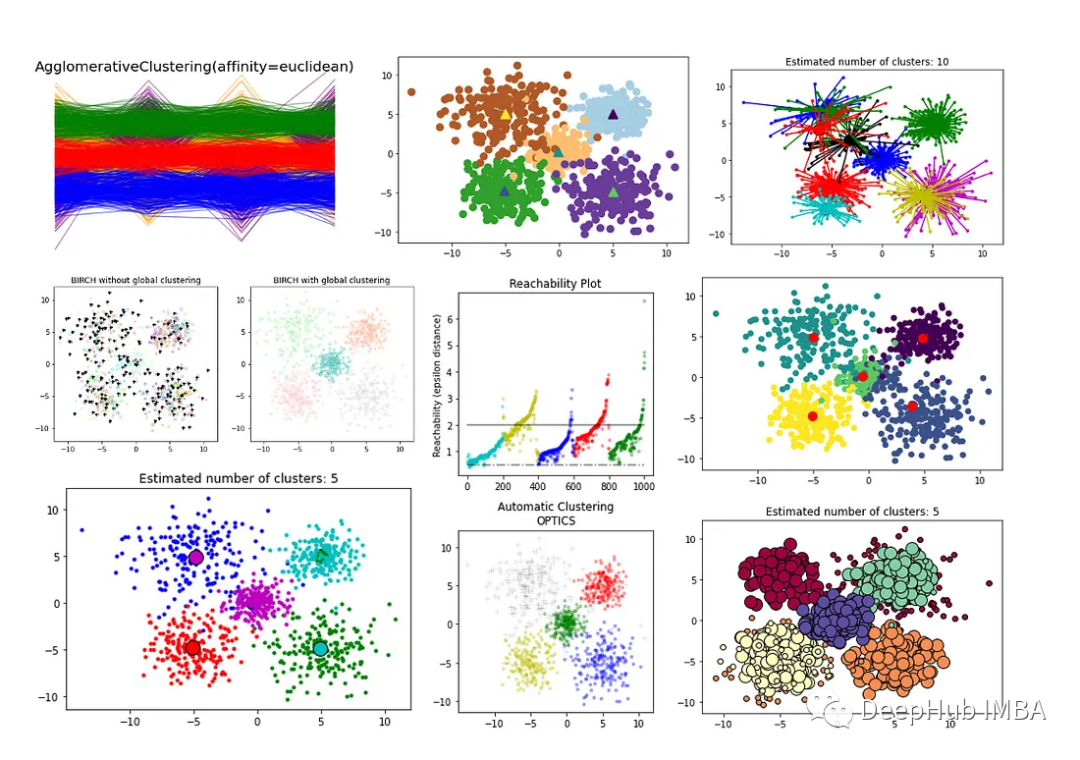
本文将全面概述Scikit-Learn库中用于的聚类技术以及各种评估方法。
本文将分为2个部分,1、常见算法比较 2、聚类技术的各种评估方法
本文作为第一部分将介绍和比较各种聚类算法:
- K-Means
- Affinity Propagation
- Agglomerative Clustering
- Mean Shift Clustering
- Bisecting K-Means
- DBSCAN
- OPTICS
- BIRCH
首先我们生成一些数据,后面将使用这些数据作为聚类技术的输入。
importpandasaspdimportnumpyasnpimportseabornassnsimportmatplotlib.pyplotasplt#Set the number of samples and featuresn_samples=1000n_features=4#Create an empty array to store the datadata=np.empty((n_samples, n_features))#Generate random data for each featureforiinrange(n_features):data[:, i] =np.random.normal(size=n_samples)#Create 5 clusters with different densities and centroidscluster1=data[:200, :] +np.random.normal(size=(200, n_features), scale=0.5)cluster2=data[200:400, :] +np.random.normal(size=(200, n_features), scale=1) +np.array([5,5,5,5])cluster3=data[400:600, :] +np.random.normal(size=(200, n_features), scale=1.5) +np.array([-5,-5,-5,-5])cluster4=data[600:800, :] +np.random.normal(size=(200, n_features), scale=2) +np.array([5,-5,5,-5])cluster5=data[800:, :] +np.random.normal(size=(200, n_features), scale=2.5) +np.array([-5,5,-5,5])#Combine the clusters into one datasetX=np.concatenate((cluster1, cluster2, cluster3, cluster4, cluster5))# Plot the dataplt.scatter(X[:, 0], X[:, 1])plt.show()
结果如下:

我们将用特征值和簇ID创建一个DF。稍后在模型性能时将使用这些数据。
df=pd.DataFrame(X, columns=["feature_1", "feature_2", "feature_3", "feature_4"])cluster_id=np.concatenate((np.zeros(200), np.ones(200), np.full(200, 2), np.full(200, 3), np.full(200, 4)))df["cluster_id"] =cluster_iddf
现在我们将构建和可视化8个不同的聚类模型:
1、K-Means
K-Means聚类算法是一种常用的聚类算法,它将数据点分为K个簇,每个簇的中心点是其所有成员的平均值。K-Means算法的核心是迭代寻找最优的簇心位置,直到达到收敛状态。
K-Means算法的优点是简单易懂,计算速度较快,适用于大规模数据集。但是它也存在一些缺点,例如对于非球形簇的处理能力较差,容易受到初始簇心的选择影响,需要预先指定簇的数量K等。此外,当数据点之间存在噪声或者离群点时,K-Means算法可能会将它们分配到错误的簇中。
#K-Meansfromsklearn.clusterimportKMeans#Define function:kmeans=KMeans(n_clusters=5)#Fit the model:km=kmeans.fit(X)km_labels=km.labels_#Print results:#print(kmeans.labels_)#Visualise results:plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, s=70, cmap='Paired')plt.scatter(kmeans.cluster_centers_[:, 0],kmeans.cluster_centers_[:, 1],marker='^', s=100, linewidth=2, c=[0, 1, 2, 3, 4])
2、Affinity Propagation
Affinity Propagation是一种基于图论的聚类算法,旨在识别数据中的"exemplars"(代表点)和"clusters"(簇)。与K-Means等传统聚类算法不同,Affinity Propagation不需要事先指定聚类数目,也不需要随机初始化簇心,而是通过计算数据点之间的相似性得出最终的聚类结果。
Affinity Propagation算法的优点是不需要预先指定聚类数目,且能够处理非凸形状的簇。但是该算法的计算复杂度较高,需要大量的存储空间和计算资源,并且对于噪声点和离群点的处理能力较弱。
fromsklearn.clusterimportAffinityPropagation#Fit the model:af=AffinityPropagation(preference=-563, random_state=0).fit(X)cluster_centers_indices=af.cluster_centers_indices_af_labels=af.labels_n_clusters_=len(cluster_centers_indices)#Print number of clusters:print(n_clusters_)importmatplotlib.pyplotaspltfromitertoolsimportcycleplt.close("all")plt.figure(1)plt.clf()colors=cycle("bgrcmykbgrcmykbgrcmykbgrcmyk")fork, colinzip(range(n_clusters_), colors):class_members=af_labels==kcluster_center=X[cluster_centers_indices[k]]plt.plot(X[class_members, 0], X[class_members, 1], col+".")plt.plot(cluster_center[0],cluster_center[1],"o",markerfacecolor=col,markeredgecolor="k",markersize=14,)forxinX[class_members]:plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)plt.title("Estimated number of clusters: %d"%n_clusters_)plt.show()

3、Agglomerative Clustering
凝聚层次聚类(Agglomerative Clustering)是一种自底向上的聚类算法,它将每个数据点视为一个初始簇,并将它们逐步合并成更大的簇,直到达到停止条件为止。在该算法中,每个数据点最初被视为一个单独的簇,然后逐步合并簇,直到所有数据点被合并为一个大簇。
Agglomerative Clustering算法的优点是适用于不同形状和大小的簇,且不需要事先指定聚类数目。此外,该算法也可以输出聚类层次结构,便于分析和可视化。缺点是计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间。此外,该算法对初始簇的选择也比较敏感,可能会导致不同的聚类结果。
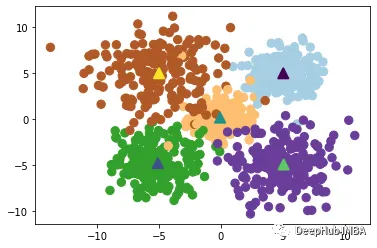
fromsklearn.clusterimportAgglomerativeClustering#Fit the model:clustering=AgglomerativeClustering(n_clusters=5).fit(X)AC_labels=clustering.labels_n_clusters=clustering.n_clusters_print("number of estimated clusters : %d"%clustering.n_clusters_)# Plot clustering resultscolors= ['purple', 'orange', 'green', 'blue', 'red']forindex, metricinenumerate([#"cosine", "euclidean", #"cityblock"]):model=AgglomerativeClustering(n_clusters=5, linkage="ward", affinity=metric)model.fit(X)plt.figure()plt.axes([0, 0, 1, 1])forl, cinzip(np.arange(model.n_clusters), colors):plt.plot(X[model.labels_==l].T, c=c, alpha=0.5)plt.axis("tight")plt.axis("off")plt.suptitle("AgglomerativeClustering(affinity=%s)"%metric, size=20)plt.show()

4、Mean Shift Clustering
Mean Shift Clustering是一种基于密度的非参数聚类算法,其基本思想是通过寻找数据点密度最大的位置(称为"局部最大值"或"高峰"),来识别数据中的簇。算法的核心是通过对每个数据点进行局部密度估计,并将密度估计的结果用于计算数据点移动的方向和距离。算法的核心是通过对每个数据点进行局部密度估计,并将密度估计的结果用于计算数据点移动的方向和距离。
Mean Shift Clustering算法的优点是不需要指定簇的数目,且对于形状复杂的簇也有很好的效果。算法还能够有效地处理噪声数据。他的缺点也是计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间,该算法还对初始参数的选择比较敏感,需要进行参数调整和优化。
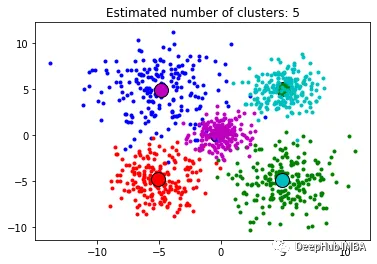
fromsklearn.clusterimportMeanShift, estimate_bandwidth# The following bandwidth can be automatically detected usingbandwidth=estimate_bandwidth(X, quantile=0.2, n_samples=100)#Fit the model:ms=MeanShift(bandwidth=bandwidth)ms.fit(X)MS_labels=ms.labels_cluster_centers=ms.cluster_centers_labels_unique=np.unique(labels)n_clusters_=len(labels_unique)print("number of estimated clusters : %d"%n_clusters_)fromitertoolsimportcycleplt.figure(1)plt.clf()colors=cycle("bgrcmykbgrcmykbgrcmykbgrcmyk")fork, colinzip(range(n_clusters_), colors):my_members=labels==kcluster_center=cluster_centers[k]plt.plot(X[my_members, 0], X[my_members, 1], col+".")plt.plot(cluster_center[0],cluster_center[1],"o",markerfacecolor=col,markeredgecolor="k",markersize=14,)plt.title("Estimated number of clusters: %d"%n_clusters_)plt.show()
5、Bisecting K-Means
Bisecting K-Means是一种基于K-Means算法的层次聚类算法,其基本思想是将所有数据点划分为一个簇,然后将该簇分成两个子簇,并对每个子簇分别应用K-Means算法,重复执行这个过程,直到达到预定的聚类数目为止。
算法首先将所有数据点视为一个初始簇,然后对该簇应用K-Means算法,将该簇分成两个子簇,并计算每个子簇的误差平方和(SSE)。然后,选择误差平方和最大的子簇,并将其再次分成两个子簇,重复执行这个过程,直到达到预定的聚类数目为止。
Bisecting K-Means算法的优点是具有较高的准确性和稳定性,能够有效地处理大规模数据集,并且不需要指定初始聚类数目。该算法还能够输出聚类层次结构,便于分析和可视化。缺点是计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间。此外该算法对初始簇的选择也比较敏感,可能会导致不同的聚类结果。
fromsklearn.clusterimportBisectingKMeans#Build and fit model:bisect_means=BisectingKMeans(n_clusters=5).fit(X)BKM_labels=bisect_means.labels_#Print model attributes:#print('Labels: ', bisect_means.labels_)print('Number of clusters: ', bisect_means.n_clusters)#Define varaibles to be included in scatterdot:y=bisect_means.labels_#print(y)centers=bisect_means.cluster_centers_# Visualize the results using a scatter plotplt.scatter(X[:, 0], X[:, 1], c=y)plt.scatter(centers[:, 0], centers[:, 1], c='r', s=100)plt.show()
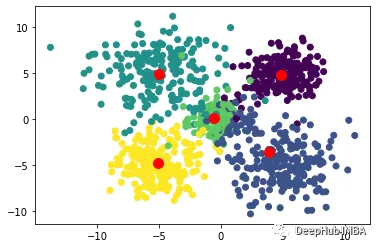
6、DBSCAN
DBSCAN (Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,其可以有效地发现任意形状的簇,并能够处理噪声数据。DBSCAN算法的核心思想是:对于一个给定的数据点,如果它的密度达到一定的阈值,则它属于一个簇中;否则,它被视为噪声点。
DBSCAN算法的优点是能够自动识别簇的数目,并且对于任意形状的簇都有较好的效果。并且还能够有效地处理噪声数据,不需要预先指定簇的数目。缺点是对于密度差异较大的数据集,可能会导致聚类效果不佳,需要进行参数调整和优化。另外该算法对于高维数据集的效果也不如其他算法
fromsklearn.clusterimportDBSCANdb=DBSCAN(eps=3, min_samples=10).fit(X)DBSCAN_labels=db.labels_# Number of clusters in labels, ignoring noise if present.n_clusters_=len(set(labels)) - (1if-1inlabelselse0)n_noise_=list(labels).count(-1)print("Estimated number of clusters: %d"%n_clusters_)print("Estimated number of noise points: %d"%n_noise_)unique_labels=set(labels)core_samples_mask=np.zeros_like(labels, dtype=bool)core_samples_mask[db.core_sample_indices_] =Truecolors= [plt.cm.Spectral(each) foreachinnp.linspace(0, 1, len(unique_labels))]fork, colinzip(unique_labels, colors):ifk==-1:# Black used for noise.col= [0, 0, 0, 1]class_member_mask=labels==kxy=X[class_member_mask&core_samples_mask]plt.plot(xy[:, 0],xy[:, 1],"o",markerfacecolor=tuple(col),markeredgecolor="k",markersize=14,)xy=X[class_member_mask&~core_samples_mask]plt.plot(xy[:, -1],xy[:, 1],"o",markerfacecolor=tuple(col),markeredgecolor="k",markersize=6,)plt.title(f"Estimated number of clusters: {n_clusters_}")plt.show()

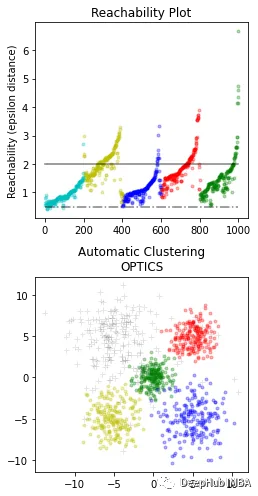
7、OPTICS
OPTICS(Ordering Points To Identify the Clustering Structure)是一种基于密度的聚类算法,其能够自动确定簇的数量,同时也可以发现任意形状的簇,并能够处理噪声数据。OPTICS算法的核心思想是:对于一个给定的数据点,通过计算它到其它点的距离,确定其在密度上的可达性,从而构建一个基于密度的距离图。然后,通过扫描该距离图,自动确定簇的数量,并对每个簇进行划分。
OPTICS算法的优点是能够自动确定簇的数量,并能够处理任意形状的簇,并能够有效地处理噪声数据。该算法还能够输出聚类层次结构,便于分析和可视化。缺点是计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间。另外就是该算法对于密度差异较大的数据集,可能会导致聚类效果不佳。
fromsklearn.clusterimportOPTICSimportmatplotlib.gridspecasgridspec#Build OPTICS model:clust=OPTICS(min_samples=3, min_cluster_size=100, metric='euclidean')# Run the fitclust.fit(X)space=np.arange(len(X))reachability=clust.reachability_[clust.ordering_]OPTICS_labels=clust.labels_[clust.ordering_]labels=clust.labels_[clust.ordering_]plt.figure(figsize=(10, 7))G=gridspec.GridSpec(2, 3)ax1=plt.subplot(G[0, 0])ax2=plt.subplot(G[1, 0])# Reachability plotcolors= ["g.", "r.", "b.", "y.", "c."]forklass, colorinzip(range(0, 5), colors):Xk=space[labels==klass]Rk=reachability[labels==klass]ax1.plot(Xk, Rk, color, alpha=0.3)ax1.plot(space[labels==-1], reachability[labels==-1], "k.", alpha=0.3)ax1.set_ylabel("Reachability (epsilon distance)")ax1.set_title("Reachability Plot")# OPTICScolors= ["g.", "r.", "b.", "y.", "c."]forklass, colorinzip(range(0, 5), colors):Xk=X[clust.labels_==klass]ax2.plot(Xk[:, 0], Xk[:, 1], color, alpha=0.3)ax2.plot(X[clust.labels_==-1, 0], X[clust.labels_==-1, 1], "k+", alpha=0.1)ax2.set_title("Automatic Clustering\nOPTICS")plt.tight_layout()plt.show()
8、BIRCH
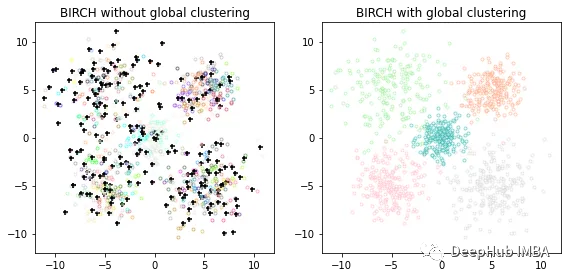
BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)是一种基于层次聚类的聚类算法,其可以快速地处理大规模数据集,并且对于任意形状的簇都有较好的效果。BIRCH算法的核心思想是:通过对数据集进行分级聚类,逐步减小数据规模,最终得到簇结构。BIRCH算法采用一种类似于B树的结构,称为CF树,它可以快速地插入和删除子簇,并且可以自动平衡,从而确保簇的质量和效率。
BIRCH算法的优点是能够快速处理大规模数据集,并且对于任意形状的簇都有较好的效果。该算法对于噪声数据和离群点也有较好的容错性。缺点是对于密度差异较大的数据集,可能会导致聚类效果不佳,对于高维数据集的效果也不如其他算法。
importmatplotlib.colorsascolorsfromsklearn.clusterimportBirch, MiniBatchKMeansfromtimeimporttimefromitertoolsimportcycle# Use all colors that matplotlib provides by default.colors_=cycle(colors.cnames.keys())fig=plt.figure(figsize=(12, 4))fig.subplots_adjust(left=0.04, right=0.98, bottom=0.1, top=0.9)# Compute clustering with BIRCH with and without the final clustering step# and plot.birch_models= [Birch(threshold=1.7, n_clusters=None),Birch(threshold=1.7, n_clusters=5),]final_step= ["without global clustering", "with global clustering"]forind, (birch_model, info) inenumerate(zip(birch_models, final_step)):t=time()birch_model.fit(X)print("BIRCH %s as the final step took %0.2f seconds"% (info, (time() -t)))# Plot resultlabels=birch_model.labels_centroids=birch_model.subcluster_centers_n_clusters=np.unique(labels).sizeprint("n_clusters : %d"%n_clusters)ax=fig.add_subplot(1, 3, ind+1)forthis_centroid, k, colinzip(centroids, range(n_clusters), colors_):mask=labels==kax.scatter(X[mask, 0], X[mask, 1], c="w", edgecolor=col, marker=".", alpha=0.5)ifbirch_model.n_clustersisNone:ax.scatter(this_centroid[0], this_centroid[1], marker="+", c="k", s=25)ax.set_ylim([-12, 12])ax.set_xlim([-12, 12])ax.set_autoscaley_on(False)ax.set_title("BIRCH %s"%info)plt.show()
总结
上面就是我们常见的8个聚类算法,我们对他们进行了简单的说明和比较,并且用sklearn演示了如何使用,在下一篇文章中我们将介绍聚类模型评价方法。
https://avoid.overfit.cn/post/e8ecff6dce514fbbbad9c6d6b882fe4e
相关文章:

聚类算法(上):8个常见的无监督聚类方法介绍和比较
无监督聚类方法的评价指标必须依赖于数据和聚类结果的内在属性,例如聚类的紧凑性和分离性,与外部知识的一致性,以及同一算法不同运行结果的稳定性。 本文将全面概述Scikit-Learn库中用于的聚类技术以及各种评估方法。 本文将分为2个部分&…...
)
华为OD机试真题Python实现【找到它】真题+解题思路+代码(20222023)
找到它 题目 找到它是个小游戏,你需要在一个矩阵中找到给定的单词 假设给定单词HELLOWORLD,在矩阵中只要能找HELLOWORLD就算通过 注意区分英文字母大小写,并且你只能上下左右行走 不能走回头路 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目…...

English Learning - L2 语音作业打卡 Day4 2023.2.24 周五
English Learning - L2 语音作业打卡 Day4 2023.2.24 周五💌 发音小贴士:💌 当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [u:]&#x…...
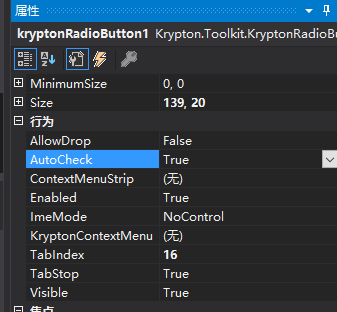
C#:Krypton控件使用方法详解(第九讲) ——kryptonRadioButton
今天介绍的Krypton控件中的kryptonRadioButton,这是一个单选按钮控件。下面开始介绍这个控件的属性:首先介绍的是外观属性,如下图所示:Cheacked属性:表示设置kryptonRadioButton控件的初始选中状态是什么样的ÿ…...
)
消失的数字(每日一题)
目录 一、题目描述 二、题目分析 2.1 方法一 2.1.1 思路 2.1.2 代码 2.2 方法二 2.2.1 思路 2.2.2 代码 2.3 方法三 2.3.1 思路 2.3.2 代码 三、完整代码 一、题目描述 oj链接:https://leetcode.cn/problems/missing-number-lcci 数组nums包含从0到n的…...

TypeScript算法基础——TS字符串的常用操作总结:substring、indexOf、slice、replace等
字符串的操作是算法题当中经常碰见的一类题目,主要考察对string类型的处理和运用。 在处理字符串的时候,我们经常会碰到求字符串长度、匹配子字符串、替换字符串内容、连接字符串、提取字符串字符等操作,那么调用一些简单好用的api可以让工作…...

Leetcode100-两数之和
参见官方题解 一、学到的知识 正面寻找两个数之和相加等于某个数,如 ab c,不如反过来寻找 a c - b 正面寻找需要两层 for 循环,把每个数都进行遍历,所以时间复杂度较高 反过来则可以通过维护一个 a 的集合,每次通过…...

4565: 删除中间的*
描述规定输入的字符串中只包含字母和*号,除了字符串前导和尾部的*号之外,将串中其他*号全部删除输入输入数据包括一串字符串,只包含字母和*,总长度不超过80。输出输出删除中间*后的字符串。样例输入*******A*BC*DEF*G****样例输出*******ABCD…...

VUE组件示例说明
<!-- * Author: xxx.xx * Date: 2021-07-20 14:33:41 * LastEditors: xxx.xx * LastEditTime: 2021-07-20 18:22:37 * PageTitle: 上拉加载组件 * Description: 描述... * FilePath: /wxapp-view/components/loadmore.vue --> <template><view class"c-mor…...
Widget中的State-学习笔记
Widget 有 StatelessWidget 和 StatefulWidget 两种类型。StatefulWidget 应对有交互、需要动态变化视觉效果的场景,而 StatelessWidget 则用于处理静态的、无状态的视图展示。StatefulWidget 的场景已经完全覆盖了 StatelessWidget,因此我们在构建界面时…...
)
股市实战技巧(知行合一)
投资策略 长线:优质核心股票大仓位核心标的票,小仓位短线投资投机小储蓄可加大投机仓位价值投资也要去做仓位控制 行情好,总体大仓位,行情小,小仓位个股根据走势调整个股仓位(布林线的20%原则)…...

k8s-资源限制-探针检查
文章目录一、资源限制1、资源限制的使用2、reuqest资源(请求)和limit资源(约束)3、Pod和容器的资源请求和限制4、官方文档示例5、资源限制实操5.1 编写yaml资源配置清单5.2 释放内存(node节点,以node01为例…...

一文让你彻底了解Linux内核文件系统
一,文件系统特点 文件系统要有严格的组织形式,使得文件能够以块为单位进行存储。文件系统中也要有索引区,用来方便查找一个文件分成的多个块都存放在了什么位置。如果文件系统中有的文件是热点文件,近期经常被读取和写入…...

解决前端组件下拉框选择功能失效问题
问题: 页面下拉框选择功能失效 现象: 在下拉框有默认值的情况下,点击下拉框的其他值,发现并没有切换到其他值 但是在下拉框没默认值的情况下,功能就正常 原因 select 已经绑定选项(有默认值) 在…...

Linux_vim编辑器入门级详细教程
前言(1)vim编辑器其实本质上就是对文本进行编辑,比如在.c文件中改写程序,在.txt文件写笔记什么的。一般来说,我们可以在windows上对文本进行编译,然后上传给Linux。但是有时候我们可能只是对文本进行简单的…...

TCP 的演化史-TCP 是一个过渡
TCP 诞生于 1970 年代早期,彼时没有分组交换网的大规模应用,彼时绝大多数通信都在使用电话,电报,电挂等电路交换技术。 诞生在这种环境下的技术不可能脱离时代的影响,如果一个孩子出生在一个父母关系冷漠的家庭&#x…...

Flask
Flask第三方组件非常全,适合小型 API服务类项目,但第三方组件运行稳定性相对Django差。 基础知识 Flask安装 pip install flask2.0.3Flask库文件 Jinjia2:模板渲染库Markupsafe:返回安全标签 只要Flask返回模板或者标签时都会…...

SAP系统与MES系统的数据协同技术方案
1.MES介绍 本文中提到的MES系统是在西门子公司的SIMATIC IT平台上开发完成。所有的应用子系统进行统一分析、统一设计、统一开发,利用统一的开发平台和数据库系统,保证了管理系统的集成性、高效性。 2.数据协同接口包含的…...
2018年蓝桥杯省赛试题-5道(Python)
文章目录一、日志统计思考二、递增三元组思考三、螺旋折线思考四、乘积最大思考五、全球变暖思考尾声提示:以下是本篇文章正文内容,下面案例可供参考 一、日志统计 题目描述 小明维护着一个程序员论坛。 现在他收集了一份"点赞"日志…...

Python稀疏矩阵最小二乘法
文章目录最小二乘法返回值测试最小二乘法 scipy.sparse.linalg实现了两种稀疏矩阵最小二乘法lsqr和lsmr,前者是经典算法,后者来自斯坦福优化实验室,据称可以比lsqr更快收敛。 这两个函数可以求解AxbAxbAxb,或arg minx∥Ax−b…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
