LeetCode 面试题 16.09. 运算
文章目录
- 一、题目
- 二、C# 题解
一、题目
请实现整数数字的乘法、减法和除法运算,运算结果均为整数数字,程序中只允许使用加法运算符和逻辑运算符,允许程序中出现正负常数,不允许使用位运算。
你的实现应该支持如下操作:
Operations()构造函数minus(a, b)减法,返回a - bmultiply(a, b)乘法,返回a * bdivide(a, b)除法,返回a / b
示例:
Operations operations = new Operations();
operations.minus(1, 2); //返回-1
operations.multiply(3, 4); //返回12
operations.divide(5, -2); //返回-2
提示:
- 你可以假设函数输入一定是有效的,例如不会出现除法分母为0的情况
- 单个用例的函数调用次数不会超过1000次
点击此处跳转题目。
二、C# 题解
使用常数数组 Poss 和 Negs 分别记录 2 次幂的正负值,便于后续使用。
P o s s : { 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7 } N e g s : { − 2 0 − 2 1 − 2 2 − 2 3 − 2 4 − 2 5 − 2 6 − 2 7 } \begin{array}{l} \hspace{0.15em}Poss:\{\hspace{0.78em} 2^0 \hspace{2.2em} 2^1 \hspace{2.25em} 2^2 \hspace{2.4em} 2^3 \hspace{2.1em} 2^4 \hspace{2.25em} 2^5 \hspace{2.25em} 2^6 \hspace{2.1em} 2^7\} \\ Negs:\{-2^0 \hspace{1em} -2^1 \hspace{1em} -2^2 \hspace{1.2em} -2^3 \hspace{0.9em} -2^4 \hspace{1em} -2^5 \hspace{1em} -2^6 \hspace{0.9em} -2^7\} \\ \end{array} Poss:{2021222324252627}Negs:{−20−21−22−23−24−25−26−27}
Negative(int a):
如果 a 是正数,则遍历负数数组Negs;如果 a 是负数,则遍历正数数组Poss。每次遍历判断相加后是否溢出,如果不溢出,就相加,否则跳过。
溢出判断条件:ans + nums[i] + a与a异号,则溢出。
a : 13 ⟵ 方向 n u m s : { − 2 0 ‾ − 2 1 − 2 2 ‾ − 2 3 ‾ − 2 4 − 2 5 − 2 6 − 2 7 } ↑ ↑ ↑ a n s : ( − 1 ) + ( − 4 ) + ( − 8 ) = − 13 \begin{array}{l} \hspace{2em}a:13\\ \hspace{25.9em} \longleftarrow 方向\\ nums:\{\underline{\bold{-2^0}} \hspace{1em} -2^1 \hspace{1em} \underline{\bold{-2^2}} \hspace{1.2em} \underline{\bold{-2^3}} \hspace{0.9em} -2^4 \hspace{1em} -2^5 \hspace{1em} -2^6 \hspace{0.9em} -2^7\} \\ \hspace{4.5em} \uparrow \hspace{5.6em} \uparrow \hspace{2.6em} \uparrow \\ \hspace{0.9em}ans:\hspace{0.3em} (-1) \hspace{1.35em} + \hspace{1.35em} (-4) \hspace{0em} + \hspace{0em} (-8) \hspace{12.5em} = -13\ \end{array} a:13⟵方向nums:{−20−21−22−23−24−25−26−27}↑↑↑ans:(−1)+(−4)+(−8)=−13
-
Minus(int a, int b):
即 a + Negative(b)。 -
Multipy(int a, int b):
类似 Negative(int a) 的思想,Negative(int a) 可以看做是 Multipy(-1, int a),因此将 nums 数组扩展为 a * 2i 即可求解 a * b。在求解 -b 时(记为 cnt),累加 a * 2i,即可得到答案。
这里需要注意 a 的符号,如果 b < 0,需要将 a 异号。
a : 5 b : − 13 c n t : ( − 1 ) + ( − 4 ) + ( − 8 ) = − 13 ↓ ↓ ↓ c n t s : { 2 0 ‾ 2 1 2 2 ‾ 2 3 ‾ 2 4 2 5 2 6 2 7 } ⟵ 方向 n u m s : { − 5 ∗ 2 0 ‾ − 5 ∗ 2 1 − 5 ∗ 2 2 ‾ − 5 ∗ 2 3 ‾ − 5 ∗ 2 4 − 5 ∗ 2 5 − 5 ∗ 2 6 − 5 ∗ 2 7 } ↑ ↑ ↑ a n s : ( − 5 ∗ 1 ) + ( − 5 ∗ 4 ) + ( − 5 ∗ 8 ) = − 5 ∗ 13 \begin{array}{l} \hspace{2em}a:5 \hspace{2em} b:-13\\\\ \hspace{1.1em} cnt: \hspace{1.1em} (-1) \hspace{2.9em} + \hspace{2.9em} (-4) \hspace{0.8em} + \hspace{0.8em} (-8) \hspace{19em} = -13\\ \hspace{5.2em} \downarrow \hspace{8.7em} \downarrow \hspace{4.2em} \downarrow \\ \hspace{0.6em} cnts: \{ \hspace{1.2em} \underline{\bold{2^0}} \hspace{3.6em} 2^1 \hspace{3.6em} \underline{\bold{2^2}} \hspace{3.6em} \underline{\bold{2^3}} \hspace{3.6em} 2^4 \hspace{3.6em} 2^5 \hspace{3.6em} 2^6 \hspace{3.6em} 2^7 \hspace{0.9em} \}\\\\ \hspace{38em} \longleftarrow 方向\\\\ nums:\{\underline{\bold{-5*2^0}} \hspace{1em} -5*2^1 \hspace{1em} \underline{\bold{-5*2^2}} \hspace{1.2em} \underline{\bold{-5*2^3}} \hspace{0.9em} -5*2^4 \hspace{1em} -5*2^5 \hspace{1em} -5*2^6 \hspace{0.9em} -5*2^7\} \\ \hspace{5.2em} \uparrow \hspace{8.7em} \uparrow \hspace{4.2em} \uparrow \\ \hspace{0.9em}ans:\hspace{0.3em} (-5*1) \hspace{2.2em} + \hspace{2.2em} (-5*4) \hspace{0em} + \hspace{0em} (-5*8) \hspace{18.5em} = -5*13\\ \end{array} a:5b:−13cnt:(−1)+(−4)+(−8)=−13↓↓↓cnts:{2021222324252627}⟵方向nums:{−5∗20−5∗21−5∗22−5∗23−5∗24−5∗25−5∗26−5∗27}↑↑↑ans:(−5∗1)+(−5∗4)+(−5∗8)=−5∗13
Divide(int a, int b):
对 b 进行扩展为 nums,即 nums = b * Poss(若 a、b 异号,则 b 取反,目的是使 nums 符号与 a 相同),让 a 尝试依次减去 nums[i],能减则减,减去后 ans 加上对应的 cnts[i](若 a、b 异号,则 cnts 数组为负值;反之,cnts 数组为正值)。是否选取第 i 个元素的条件:
1. a > 0,则 sum + nums[i] <= a。
2. a < 0,则 sum + nums[i] >= a。
a : − 67 b : 5 a n s : ( − 1 ) + ( − 4 ) + ( − 8 ) = − 13 ↓ ↓ ↓ c n t s : { − 2 0 ‾ − 2 1 − 2 2 ‾ − 2 3 ‾ − 2 4 − 2 5 − 2 6 − 2 7 } ⟵ 方向 n u m s : { − 5 ∗ 2 0 ‾ − 5 ∗ 2 1 − 5 ∗ 2 2 ‾ − 5 ∗ 2 3 ‾ − 5 ∗ 2 4 − 5 ∗ 2 5 − 5 ∗ 2 6 − 5 ∗ 2 7 } ↑ ↑ ↑ s u m : ( − 65 ) ← ( − 60 ) ← ( − 40 ) = − 5 ∗ 13 \begin{array}{l} \hspace{2em}a:-67 \hspace{2em} b:5\\\\ \hspace{0.9em} ans: \hspace{1.1em} (-1) \hspace{2.9em} + \hspace{2.9em} (-4) \hspace{0.8em} + \hspace{0.8em} (-8) \hspace{19em} = -13\\ \hspace{5.2em} \downarrow \hspace{8.7em} \downarrow \hspace{4.2em} \downarrow \\ \hspace{0.6em} cnts: \{ \hspace{0.8em} \underline{\bold{-2^0}} \hspace{2.6em} -2^1 \hspace{2.6em} \underline{\bold{-2^2}} \hspace{2.6em} \underline{\bold{-2^3}} \hspace{2.6em} -2^4 \hspace{2.5em} -2^5 \hspace{2.4em} -2^6 \hspace{2.4em} -2^7 \hspace{0.4em} \}\\\\ \hspace{38em} \longleftarrow 方向\\\\ nums:\{\underline{\bold{-5*2^0}} \hspace{1em} -5*2^1 \hspace{1em} \underline{\bold{-5*2^2}} \hspace{1.2em} \underline{\bold{-5*2^3}} \hspace{0.9em} -5*2^4 \hspace{1em} -5*2^5 \hspace{1em} -5*2^6 \hspace{0.9em} -5*2^7\} \\ \hspace{5.2em} \uparrow \hspace{8.7em} \uparrow \hspace{4.2em} \uparrow \\ \hspace{0.6em}sum:\hspace{0.9em} (-65) \hspace{2.5em} \leftarrow \hspace{2.5em} (-60) \hspace{0.3em} \leftarrow \hspace{0.3em} (-40) \hspace{18.8em} = -5*13\\ \end{array} a:−67b:5ans:(−1)+(−4)+(−8)=−13↓↓↓cnts:{−20−21−22−23−24−25−26−27}⟵方向nums:{−5∗20−5∗21−5∗22−5∗23−5∗24−5∗25−5∗26−5∗27}↑↑↑sum:(−65)←(−60)←(−40)=−5∗13
public class Operations {private static long[] Negs, Poss;private const int NEG_ONE = -1;private const int ARR_LEN = 32;static Operations() {long p = 1, n = -1;Poss = new long[ARR_LEN];Negs = new long[ARR_LEN];for (int i = 0; i < ARR_LEN; i++) { // 初始化正、负数组Poss[i] = p;p += p;Negs[i] = n;n += n;}}public int Minus(int a, int b) {return (int)(a + Negative(b));}public int Multiply(int a, int b) {if (a == 0 || b == 0) return 0;long p = b > 0 ? a : Negative(a), ans = 0, cnt = 0;long[] cnts = b > 0 ? Negs : Poss, nums = new long[ARR_LEN];for (int i = 0; i < ARR_LEN; i++) { // 初始化记录数组nums[i] = p;p += p;}// 计算 -b 的过程中,同比例计算 ansfor (int i = ARR_LEN + NEG_ONE; i >= 0; i += NEG_ONE) {if (SameSignal(cnt + cnts[i] + b, b)) {cnt += cnts[i];ans += nums[i];}if (cnt + b == 0) return (int)ans;}return (int)ans;}public int Divide(int a, int b) {if (a == 0) return 0;long p = SameSignal(a, b) ? b : Negative(b), sum = 0, ans = 0;long[] cnts = SameSignal(a, b) ? Poss : Negs, nums = new long[ARR_LEN];for (int i = 0; i < ARR_LEN; i++) { // 初始化记录数组nums[i] = p;p += p;}for (int i = ARR_LEN + NEG_ONE; i >= 0; i += NEG_ONE) {// a > 0,则用 <= 判断溢出,a < 0,则用 >= 判断溢出if (a > 0 && sum + nums[i] <= a || a < 0 && sum + nums[i] >= a) {sum += nums[i];ans += cnts[i];}}return (int)ans;}// 求 -apublic long Negative(long a) {if (a == 0) return 0;long[] nums = a > 0 ? Negs : Poss; // 寻找与 a 异号的数组long ans = 0;for (int i = ARR_LEN + NEG_ONE; i >= 0; i += NEG_ONE) { // 绝对值大 -> 小遍历if (SameSignal(ans + nums[i] + a, a)) // ans + nums[i] 未溢出,则加上 nums[i]ans += nums[i];if (ans + a == 0) return ans; // 提前返回}return ans;}// 判断 a、b 符号是否相同// 0 既看作正数也看作负数public bool SameSignal(long a, long b) {return a <= 0 && b <= 0 || a >= 0 && b >= 0;}
}/*** Your Operations object will be instantiated and called as such:* Operations obj = new Operations();* int param_1 = obj.Minus(a,b);* int param_2 = obj.Multiply(a,b);* int param_3 = obj.Divide(a,b);*/
- 时间:104 ms,击败 80.00% 使用 C# 的用户
- 内存:48.40 MB,击败 0.00% 使用 C# 的用户
相关文章:

LeetCode 面试题 16.09. 运算
文章目录 一、题目二、C# 题解 一、题目 请实现整数数字的乘法、减法和除法运算,运算结果均为整数数字,程序中只允许使用加法运算符和逻辑运算符,允许程序中出现正负常数,不允许使用位运算。 你的实现应该支持如下操作:…...
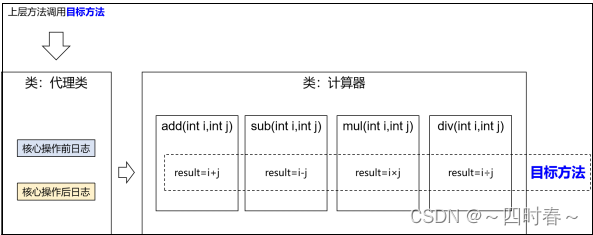
spring-代理模式
代理模式 一、概念1.静态代理2.动态代理 一、概念 ①介绍 二十三种设计模式中的一种,属于结构型模式。它的作用就是通过提供一个代理类,让我们在调用目标 方法的时候,不再是直接对目标方法进行调用,而是通过代理类间接调用。让不…...
我用好说 AI 做二次元人设
你有没有想过自己做一部原创作品? 就像开发《星露谷物语》那样,自己把控作品的 角色、故事、载体、宣传 等方方面面,让 idea 不再只是灵光一闪。 以前是 “万事开头难”,可能第一步都举步维艰。但现在有了 AI 就不同了ÿ…...

付费阅读微信小程序源码/小程序和公众号双版本-多种付费模式前后端+独立源码
源码简介: 付费阅读微信小程序源码,这个是小程序和公众号双版本,它支持多种付费模式前后端独立源码。能够支持免费观看部分文字、视频和音频内容,而其他部分则需要付费才能继续观看。这样更方便变现。 这是付费阅读微信小程序合…...

ref、reactive、toRef、toRefs
ref 作用:定义一个响应式数据 语法:const xxx ref(initValue) 创建一个包含响应式数据的引用对象 js中操作数据:xxx.value 模板中读取数据:不需要.value,直接<div>{{xxx}}</div> 接收的数据:基本类型、对…...

GPT实战系列-如何用自己数据微调ChatGLM2模型训练
GPT实战系列-如何用自己数据微调ChatGLM2模型训练 目录 GPT实战系列-如何用自己数据微调ChatGLM2模型训练1、训练数据广告文案生成模型训练和测试数据组织: 2、训练脚本3、执行训练调整运行 4、问题解决问题一问题二问题三问题四 1、训练数据 广告文案生成模型 输…...
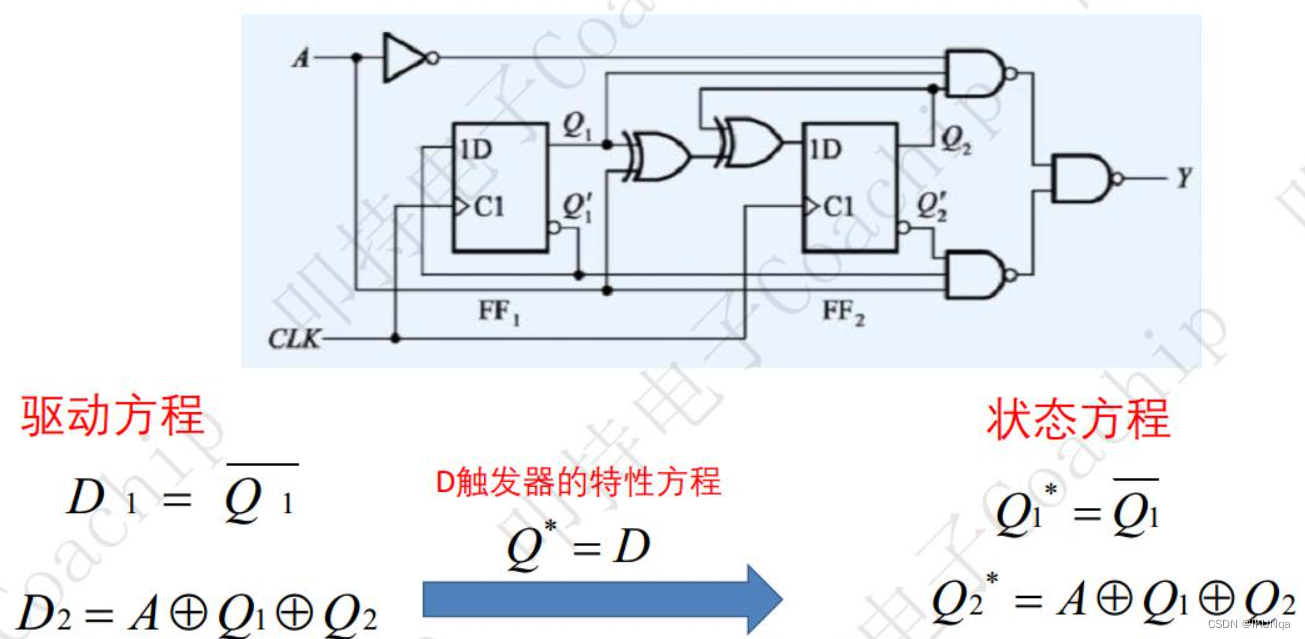
【数电知识点_2023.10.28】
数制与码制 十进制转二进制 8 bits 1 Byte 2|12 //121100自下而上 商为0为止 2|_ 6_…0 2|_ 3_…0 2|1…1 0…1 0.375 //0.3750.011自上而下 小数点为0为止 x 2 ———— 0.75…0 x 2 ———— 1.5…1 x 2 ———— 1…1 BCD码:每4位二进制表示一位十进制 8421…...
spring boot配置ssl(多cer格式)保姆级教程
1. 准备cer格式的证书; 2. 合并cer证书并转化成jks格式的证书 为啥有这一步,因为cer证书配置在spring boot项目中,项目启动不起来。如果有大佬想指导一下可以给我留言,在此先谢过大佬。 1)先创建一个jks格式的证…...
第2篇 机器学习基础 —(4)k-means聚类算法
前言:Hello大家好,我是小哥谈。聚类算法是一种无监督学习方法,它将数据集中的对象分成若干个组或者簇,使得同一组内的对象相似度较高,不同组之间的对象相似度较低。聚类算法可以用于数据挖掘、图像分割、文本分类等领域…...

【Python爬虫+可视化】解析小破站热门视频,看看播放量为啥会这么高!评论、弹幕主要围绕什么展开
大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 如果有什么疑惑/资料需要的可以点击文章末尾名片领取源码 环境使用 Python 3.8 Pycharm 模块使用 import requests import csv import datetime import hashlib import time 一. 数据来源分析 明确需求 明确采集网站以及数…...

Mac电脑专业三维模型展UV贴图编辑工具RizomUV RS + VS 2023有哪些特点
RizomUV RS VS是一款功能强大的UV展开软件,用于在三维模型上创建和编辑UV贴图。它具有直观的用户界面和丰富的功能,能够帮助艺术家和设计师更高效地进行UV展开工作。 RizomUV RS VS支持多种模型格式,包括OBJ、FBX、DAE和3DS等,使…...

Linux文件描述符和文件指针互转
本文研究的主要是Linux中文件描述符fd与文件指针FILE*互相转换的相关内容,具体介绍如下。 简介 1.文件描述符fd的定义: 文件描述符在形式上是一个非负整数。实际上,它是一个索引值,指向内核为每一个进程所维护的该进程打开文件的记录表。当…...
C++11线程
C11线程 创建线程 创建线程需要包含头文件<thread>,使用线程类std::thread 构造函数 默认构造函数 thread() noexcept; 默认构造函数,构造一个线程对象,但它不会启动任何实际的线程执行。 任务函数构造函数 template< class Fun…...

VIVO应用商店评论数据抓取
VIVO应用商店的app评论数据抓取 每个应用的评论能获取到最新的 100页 数据 每页20条,也就是 2000条评论数据 接口: pl.appstore.vivo.com.cn/port/comments/ 爬取运行截图:...

第00章_写在前面
第00章_写在前面 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.comhttp://www.atguigu.com/) 一、MySQL数据库基础篇大纲 MySQL数据库基础篇分为5个篇章: 1. 数据库概述与MySQL安装篇…...
测绘人注意,你可能会改变历史!
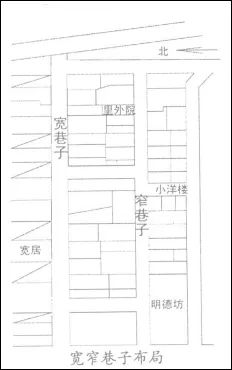
你也许想不到,曾经有一个测绘人员在进行实地测量作业时,在地图上就这么随手一标注,却让这个地方成为了如今的网红打卡地。 这个地方就是外地游客慕名而来的“宽窄巷子”,如果连这个地方都不知道的成都人,就应该不能算…...

MySQL - 慢查询
慢查询日志用于记录执行时间超过设定的时间阈值的 SQL 查询语句。它的目的是帮助数据库管理员识别和优化执行时间较长的查询,以提高数据库性能: 慢查询定义:慢查询日志记录那些执行时间超过 long_query_time 参数设定的时间阈值的 SQL 查询语…...
go中“哨兵错误”的由来及使用建议
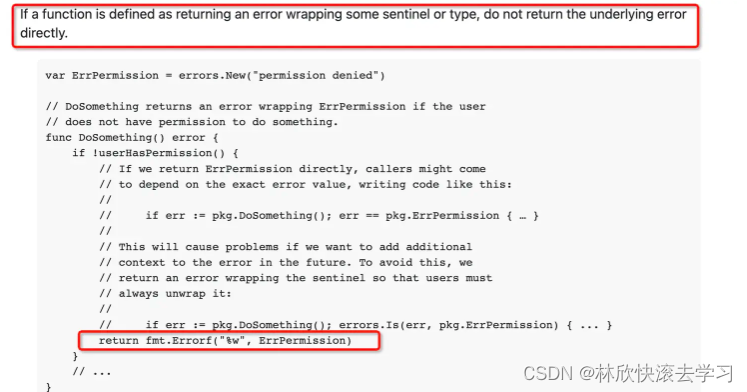
“哨兵错误(sentinel error)”这个词的出处。之前我也只是在一些书籍和资料中见到过,也没深究。当这个网友问了我之后,就深入的翻了翻资料,在golang的官方博客中找到了这个词的提法,也算是比较官方的了吧。…...

【Python百练——第2练】使用Python做一个猜数字小游戏
💐作者:insist-- 💐个人主页:insist-- 的个人主页 理想主义的花,最终会盛开在浪漫主义的土壤里,我们的热情永远不会熄灭,在现实平凡中,我们终将上岸,阳光万里 ❤️欢迎点…...
Power BI 傻瓜入门 18. 让您的数据熠熠生辉
本章内容包括: 配置Power BI以使数据增量刷新发现使用Power BI Desktop and Services保护数据集的方法在不影响性能和完整性的情况下管理海量数据集 如果有更新的、更相关的数据可用,旧数据对组织没有好处。而且,老实说,如果数据…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
