详解—数据结构《树和二叉树》
目录
一.树概念及结构
1.1树的概念
1.2树的表示
二.二叉树的概念及结构
2.1概念
2.2二叉树的特点
2.3现实中的二叉树
2.4数据结构中的二叉树
2.5 特殊的二叉树
2.6二叉树的存储结构
2.6.1二叉树的性质
2.6.2 顺序结构
2.6.3链式存储
三. 二叉树的链式结构的遍历
一.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以
有0个或多个后继
因此,树是递归定义的


节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:
A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
1.2树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; //节点中的数据域
};
二.二叉树的概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
2.2二叉树的特点
1. 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
2. 二叉树的子树有左右之分,其子树的次序不能颠倒。
2.3现实中的二叉树

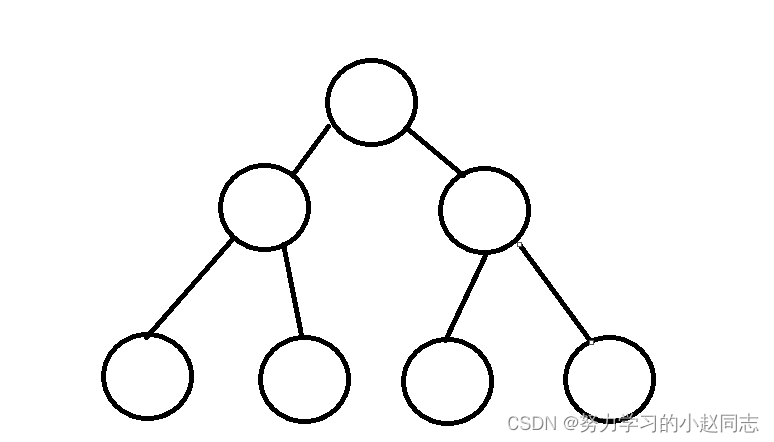
2.4数据结构中的二叉树
2.5 特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树

2.6二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构(数组顺序表),一种链式结构(链表)
2.6.1二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2+1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=Log2(n+1). (ps:Log2(n+1)是log以2为底,n+1为对数)
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2.6.2 顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

2.6.3链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链
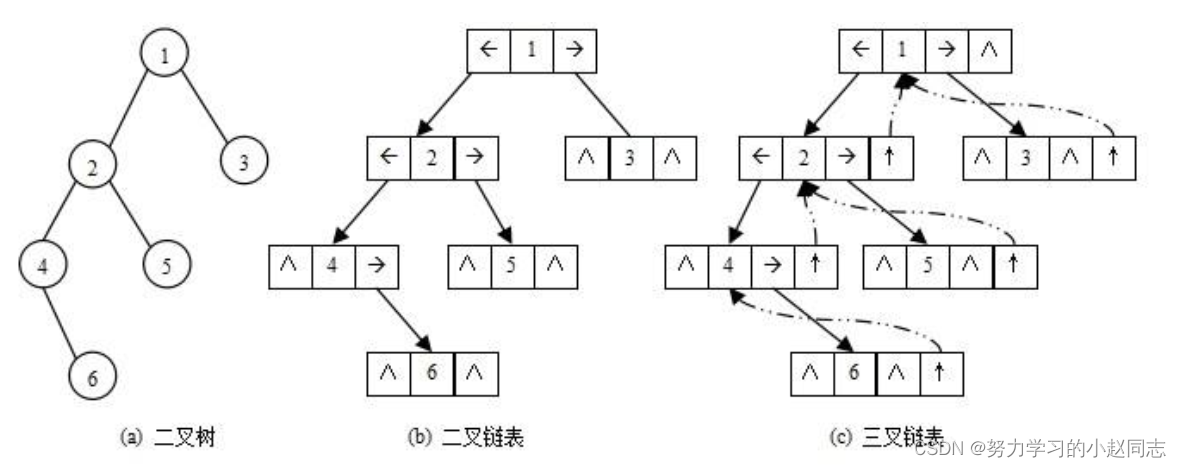
三. 二叉树的链式结构的遍历
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础
前序/中序/后序的递归结构遍历:是根据访问结点操作发生位置命名
1. NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
3. LRN:后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
2. LNR:中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
相关文章:

详解—数据结构《树和二叉树》
目录 一.树概念及结构 1.1树的概念 1.2树的表示 二.二叉树的概念及结构 2.1概念 2.2二叉树的特点 2.3现实中的二叉树 2.4数据结构中的二叉树 2.5 特殊的二叉树 2.6二叉树的存储结构 2.6.1二叉树的性质 2.6.2 顺序结构 2.6.3链式存储 三. 二叉树的链式结构的遍历 …...
菜单管理中icon图标回显
<el-table-column prop"icon" label"图标" show-overflow-tooltip algin"center"><template v-slot"{ row }"><el-icon :class"row.icon"></el-icon></template></el-table-column>...

Postman如何导出接口的几种方法
本文主要介绍了Postman如何导出接口的几种方法,文中通过示例代码介绍的非常详细,具有一定的参考价值,感兴趣的小伙伴们可以参考一下 前言: 我的文章还是一贯的作风,简确用风格(简单确实有用)&…...
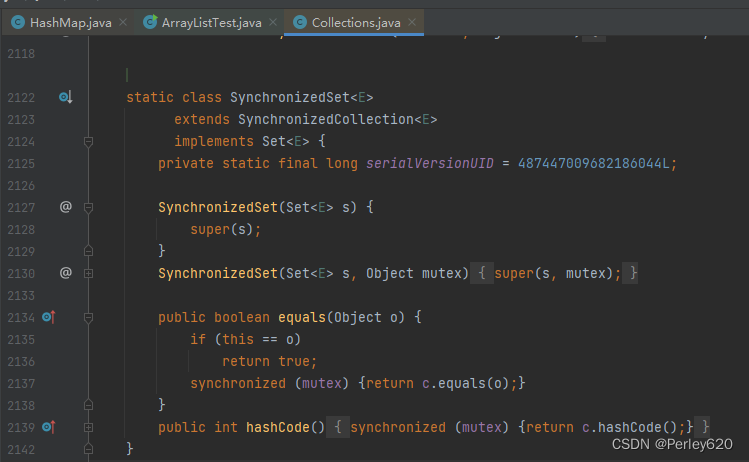
Java进阶(Set)——面试时Set常见问题解读 结合源码分析
前言 List、Set、HashMap作为Java中常用的集合,需要深入认识其原理和特性。 本篇博客介绍常见的关于Java中Set集合的面试问题,结合源码分析题目背后的知识点。 关于List的博客文章如下: Java进阶(List)——面试时L…...

【强化学习】12 —— 策略梯度(REINFORCE )
文章目录 前言策略梯度基于策略的强化学习的优缺点Example:Aliased Gridworld策略目标函数策略优化策略梯度利用有限差分计算策略梯度得分函数和似然比策略梯度定理蒙特卡洛策略梯度(Monte-Carlo Policy Gradient)Puck World Example Softmax随机策略 代…...

Kubernetes Taint(污点) 和 Toleration(容忍)
Author:rab 目录 前言一、Taint(污点)1.1 概述1.2 查看节点 Taint1.3 标记节点 Taint1.4 删除节点 Taint 二、Toleration(容忍) 前言 Kubernetes 中的污点(Taint)和容忍(Toleration…...

使用cv::FileStorage时出错 Can‘t open file: yaml‘ in read mode
1. 使用说明 在做的一个c工程项目,想加一个配置文件,我发现主要有两种主流的方式, (1)opencv有cv::FileStorage这样的一个函数可以使用。 (2)也可以使用cpp-yaml GitHub - jbeder/yaml-cpp: …...

代码之困:那些让你苦笑不得的bug
在编写代码的过程中,我们常常会遇到各种各样的bug。有的时候,我们花费了大量的时间和精力去寻找问题的根源,但却找不到任何线索。然而,令人哭笑不得的是,有时候这些问题的解决方案却是如此简单,以至于我们不…...

【C语言初学者周冲刺计划】2.2用选择法对10个整数从小到大排序
目录 1解题思路: 2代码如下: 3运行结果: 4总结: 1解题思路: 首先利用一维数组和循环语句输入10个整数,然后利用双循环的嵌套进行比较大小,最后输出结果; 2代码如下: #include&…...

c++系列——智能指针
1.智能指针的使用及原理 1.1 RAII RAII(Resource Acquisition Is Initialization)是一种利用对象生命周期来控制程序资源(如内 存、文件句柄、网络连接、互斥量等等)的简单技术。 在对象构造时获取资源,接着控制对资…...

力扣日记10.30-【栈与队列篇】滑动窗口最大值
力扣日记:【栈与队列篇】滑动窗口最大值 日期:2023.10.30 参考:代码随想录、力扣 239. 滑动窗口最大值 题目描述 难度:困难 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只…...

docker与宿主机共享内存通信
docker与宿主机共享内存通信 docker中的进程要与宿主机使用共享内存通信,需要在启动容器的时候指定“–ipchost”选项。然后再编写相应的共享内存的程序,一个跑在宿主机上,另一个跑在docker上面。 宿主机程序准备 shm_data.h #ifndef _SH…...
A股风格因子看板 (2023.10 第13期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第13期,指数组合数据截止日2023-09-30,要点如下 近1年A股风格因子检验统…...

ORB-SLAM3算法2之EuRoc、TUM和KITTI开源数据集运行ORB-SLAM3生成轨迹并用evo工具评估轨迹
文章目录 0 引言1 数据和真值1.1 TUM1.2 EuRoc1.3 KITTI2 ORB-SLAM3的EuRoc示例2.1 纯单目的示例2.2 纯单目的轨迹评估2.3 纯双目的示例2.4 纯双目的轨迹评估2.5 单目和IMU的示例2.6 单目和IMU的轨迹评估2.7 双目和IMU的示例2.8 双目和IMU的轨迹评估2.9 前四种的评估结果对比3 …...

【蓝桥杯选拔赛真题07】C++小球自由落体 青少年组蓝桥杯C++选拔赛真题 STEMA比赛真题解析
目录 C/C++小球自由落体 一、题目要求 1、编程实现 2、输入输出 二、算法分析...

期中考成绩一键私发
作为一名教师,期中考试后最繁忙的事情之一就是发布成绩。每个学生都希望尽快知道自己的成绩,而作为老师,我们需要一种更高效、更方便的方式来完成这项任务。今天,我就来给大家介绍一种成绩查询系统,让我们一起告别繁琐…...
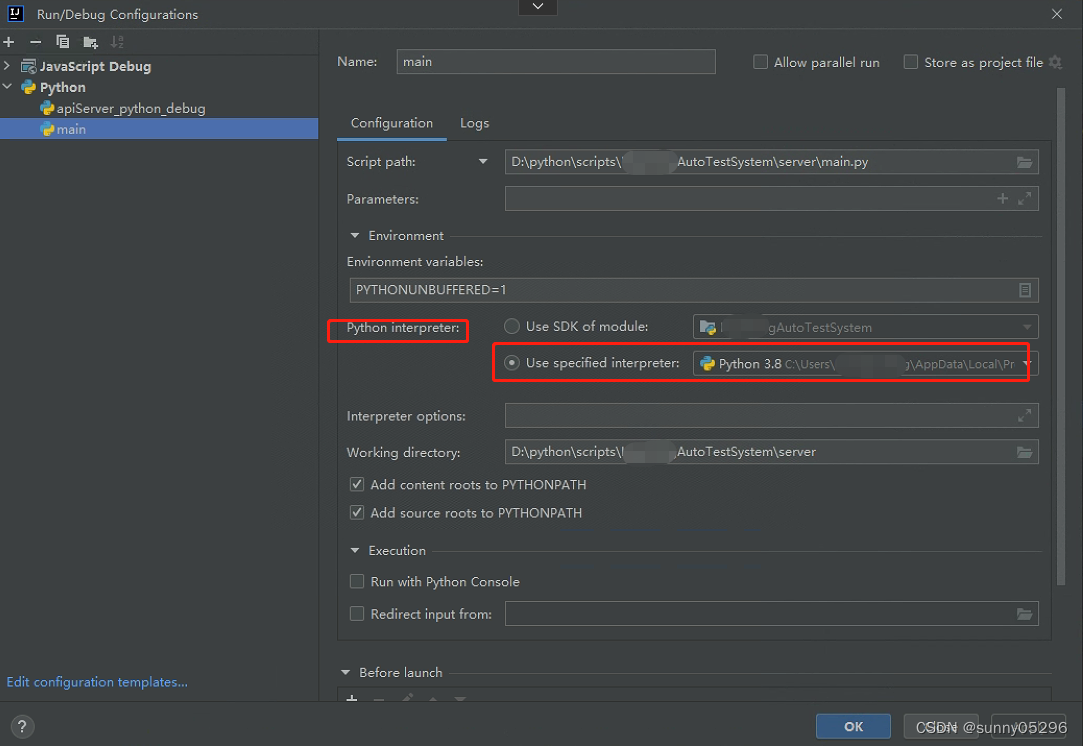
idea中Run/Debug Python项目报错 Argument for @NotNull parameter ‘module‘ of ...
idea中Run/Debug Python项目报错 Argument for NotNull parameter module of ... idea中运行Python项目main.py时报错: Error running main: Argument for NotNull parameter module of com/intellij/openapi/roots/ModuleRootManager.getInstance must not be nu…...
计算机网络第3章-TCP协议(2)
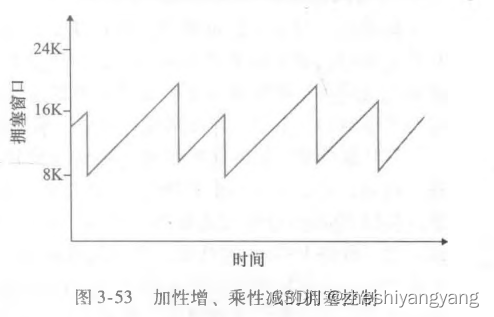
TCP拥塞控制 TCP拥塞控制的三种方式: 慢启动、拥塞避免、快速恢复 慢启动 当一条TCP连接开始时,cwnd的值是一个很小的MSS值,这使得初始发送速率大约为MSS/RTT。 在慢启动状态,cwnd的值以1个MSS开始并且每当传输的报文段首次被…...
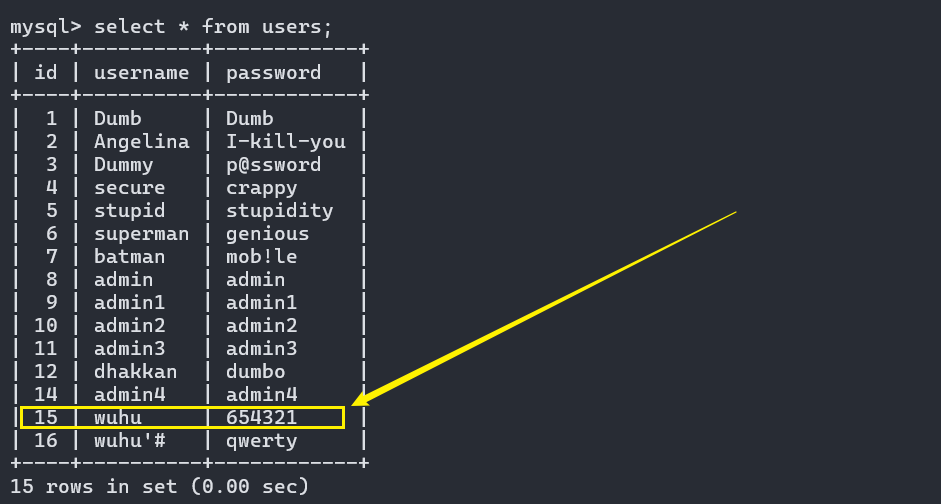
SQL注入——二次注入漏洞
文章目录 SQL注入——二次注入漏洞1. 二次注入原理2. 二次注入需要具备的两个条件3. 二次注入实例4. 总结 SQL注入——二次注入漏洞 1. 二次注入原理 在第一次插入恶意数据的时候,只是对其中的特殊字符进行了转义,在写入数据库的时候还是原来的字符&am…...
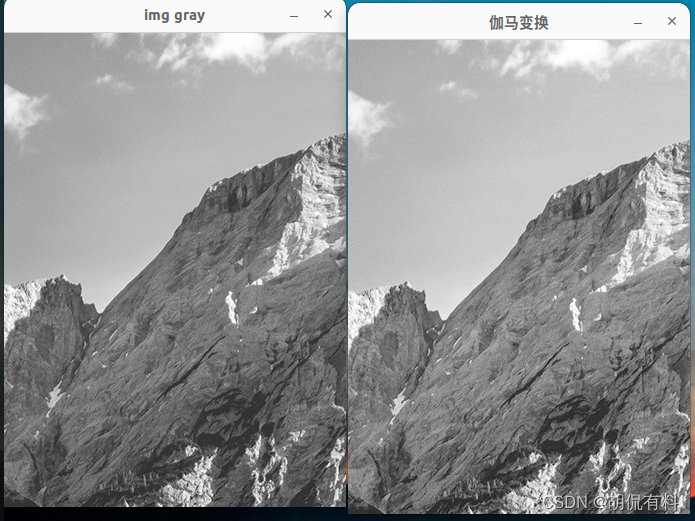
【c++|opencv】二、灰度变换和空间滤波---1.灰度变换、对数变换、伽马变换
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 灰度变换、对数变换、伽马变换 1. 灰度变换 #include <iostream> #include <opencv2/opencv.hpp>using namespace std; using namespace c…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
