【算法】Prim算法(求最小生成树)
题目
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤500
1≤m≤10^5
图中涉及边的边权的绝对值均不超过 10000
思路
建立一个集合,将距离这个集合最近的节点s放入集合内部,然后使用节点s对其他节点到集合的距离进行更新,st[s]=true;表示节点s已经被放入集合,已经放入集合的元素不能再次被放入集合。然后开始下一次循环,每次放入一个节点到集合中,一共遍历n次(一共n个点)。
代码
#include<bits/stdc++.h>
#define N 510
using namespace std;
const int INF = 0x3f3f3f3f;
int n,m;// n个点,m条边
int g[N][N];// 表示点i到点j的距离(不邻接的话为正无穷)
int dist[N];// 表示点i到集合的最小距离
bool st[N];// 表示点i是否在集合内部int prim()
{memset(dist,0x3f,sizeof(dist));// 将距离初始化为正无穷int res = 0;for(int i = 0; i < n; i ++)// 遍历n个点{int t = -1;for(int j = 1; j <= n; j ++)// 遍历所有点if(!st[j] && (t == -1 || dist[t] > dist[j]))// 找到不在集合内部,并且距离集合最近的点t = j;if(i && dist[t] == INF) return INF; // 如果找不到距离小于正无穷的点,则代表这个图不连通,没有最小生成树(当i等于零时,集合还没有元素,不能进行判断)if(i) res += dist[t];// 将这条最小边加起来,是建成最小生成树的其中一条边(当i等于零时,集合还没有元素,不能进行判断)for(int j = 1;j <= n; j ++) dist[j] = min(dist[j],g[t][j]);// 使用这个点对这其他点进行更新st[t] = true;// 这个点已经在集合内部了}return res;// 返回最小生成树的长度
}int main()
{cin >> n >> m;// 输入点数,边数memset(g,0x3f,sizeof(g));while(m --){int a,b,c;cin >> a >> b >> c;// 输入点a到点b之间的距离g[a][b] = g[b][a] = min(g[a][b],c);// 建立无向图}int t = prim();if( t == INF ) cout << "impossible" << endl;else cout << t << endl;return 0;
}相关文章:
)
【算法】Prim算法(求最小生成树)
题目 给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。 求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。 给定一张边带权的无向图 G(V,E),其中 V 表示图中点的集合,E…...

go语言,yaml实现简单的workflow工作流
目录 1.创建一个yaml文件,名字可以是student.yaml 2.创建go文件测试 3.执行结果 本文章内容,只是一个简单的案例,但足够映射到一个大的项目中。 工作流作用:工作流的作用就是通过yaml配置文件,将关于本工作流的一个…...

BaiduMallServcie
说明 本文档指导业务开发步骤 BaiduMallServcie 说明一. 登录业务1.1 数据库设计1.1.1 管理员表1.1.2 角色表1.1.3 关联表 管理员表与角色表关联1.1.4 权限表1.1.5 关联表 角色表与权限表关联1.1.6 管理员登录日志表1.1.7 查询权限示例1.2 添加用户一. 登录业务 1.1 数据库设…...
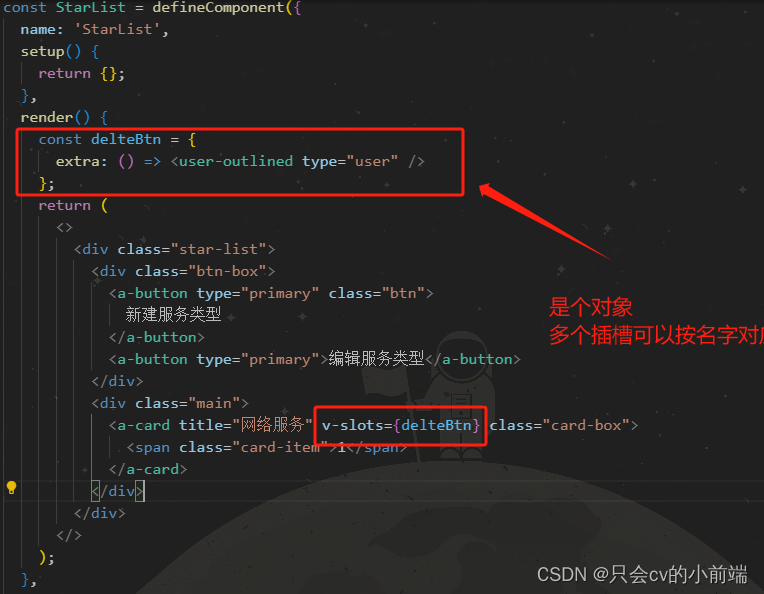
vue3+jsx+antd的插槽写法之一
如果在jsx里面直接这样按照官方的写法是会报错的 正确写法是:...

Shell 学习之 if 命令
1. 执行流程 在 Shell 脚本中,if 是一个 控制流语句,用于进行条件判断,根据条件的结果执行相应的操作。 # 首先,Shell 会检查表达式 condition 返回的 boolean 值。 # 如果 condition 的值为真,则执行 then 代码块&a…...

android 同步 服务器 时间
要将 Android 设备与服务器同步时间,可以通过以下两种方式实现: NTP 协议同步时间 NTP(Network Time Protocol)是一种网络协议,用于同步计算机的时间。Android 设备可以使用 NTP 协议来同步服务器时间。 Android 应…...
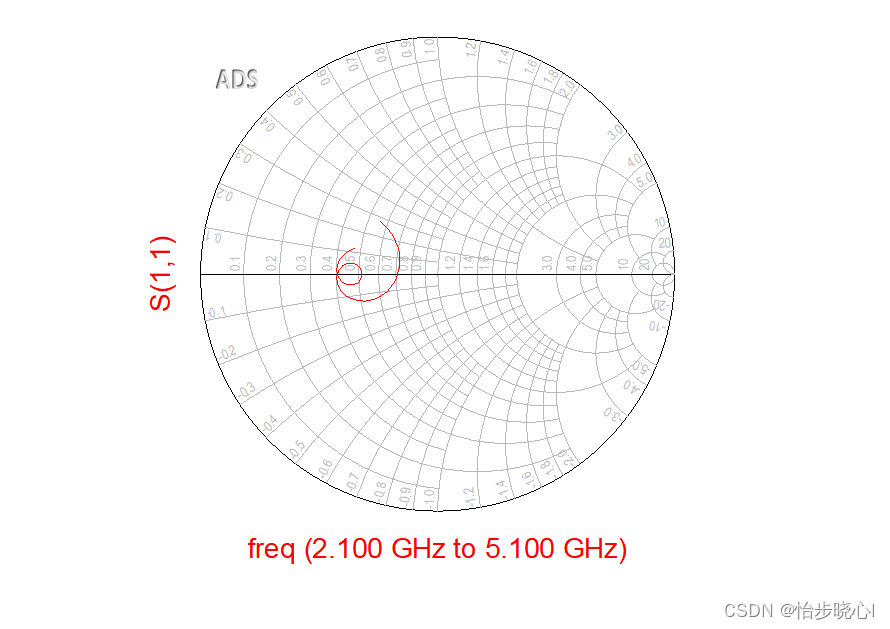
10、电路综合-基于简化实频的宽带匹配电路设计方法
10、电路综合-基于简化实频的宽带匹配电路设计方法 网络综合和简化实频理论学习概述中的1-9介绍了SRFT的一些基本概念和实验方法,终于走到了SRFT的另一个究极用途,宽带匹配电路的设计。 1、之前的一些回顾与总结 之前也给出了一些电路综合的案例&…...
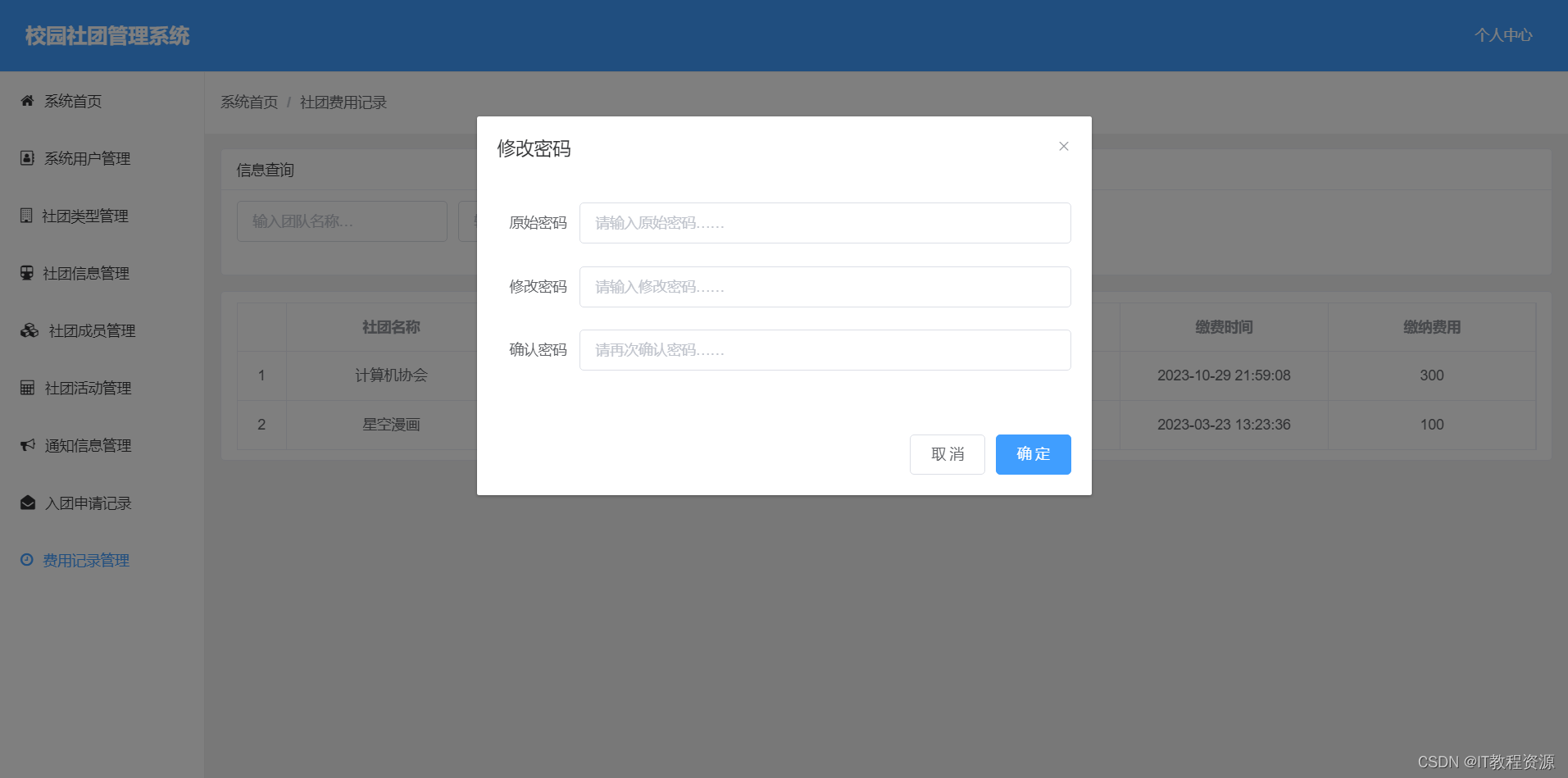
N-130基于springboot,vue校园社团管理系统
开发工具:IDEA 服务器:Tomcat9.0, jdk1.8 项目构建:maven 数据库:mysql5.7 系统分前后台,项目采用前后端分离 前端技术:vueelementUI 服务端技术:springbootmybatis-plus 本系…...
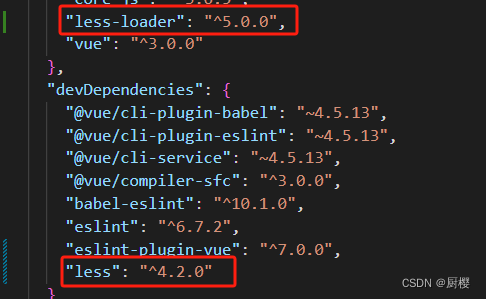
Syntax Error: TypeError: this.getOptions is not a function的解决(Vue)
报错信息: TypeError: this.getOptions is not a function 这个是在运行项目是遇到的问题 这个报错是类型错误,this.getOptions 不是一个函数 。这个错误一般就是less-loader库里的错误。 主要是less-loader版本太高,不兼容this.getOptions…...

使用 kube-downscaler 降低Kubernetes集群成本
新钛云服已累计为您分享772篇技术干货 介绍 Kube-downscaler 是一款开源工具,允许用户定义 Kubernetes 中 pod 资源自动缩减的时间。这有助于通过减少非高峰时段的资源使用量来降低基础设施成本。 在本文中,我们将详细介绍 kube-downscaler 的功能、安装…...

LeetCode热题100——哈希表
哈希表 1.两数之和2.字母异位词分组3.最长连续序列 1.两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。可以按任意顺序返回答案。 // 题解思路:使用哈…...

Kubeadm
目录 绪论:实验步骤 1、环境准备 2、所有节点安装docker 3、所有节点安装kubeadm,kubelet和kubectl 4、部署K8S集群 5、部署 Dashboard 6、安装Harbor私有仓库 master(2C/4G,cpu核心数要求大于2) 192.168.…...
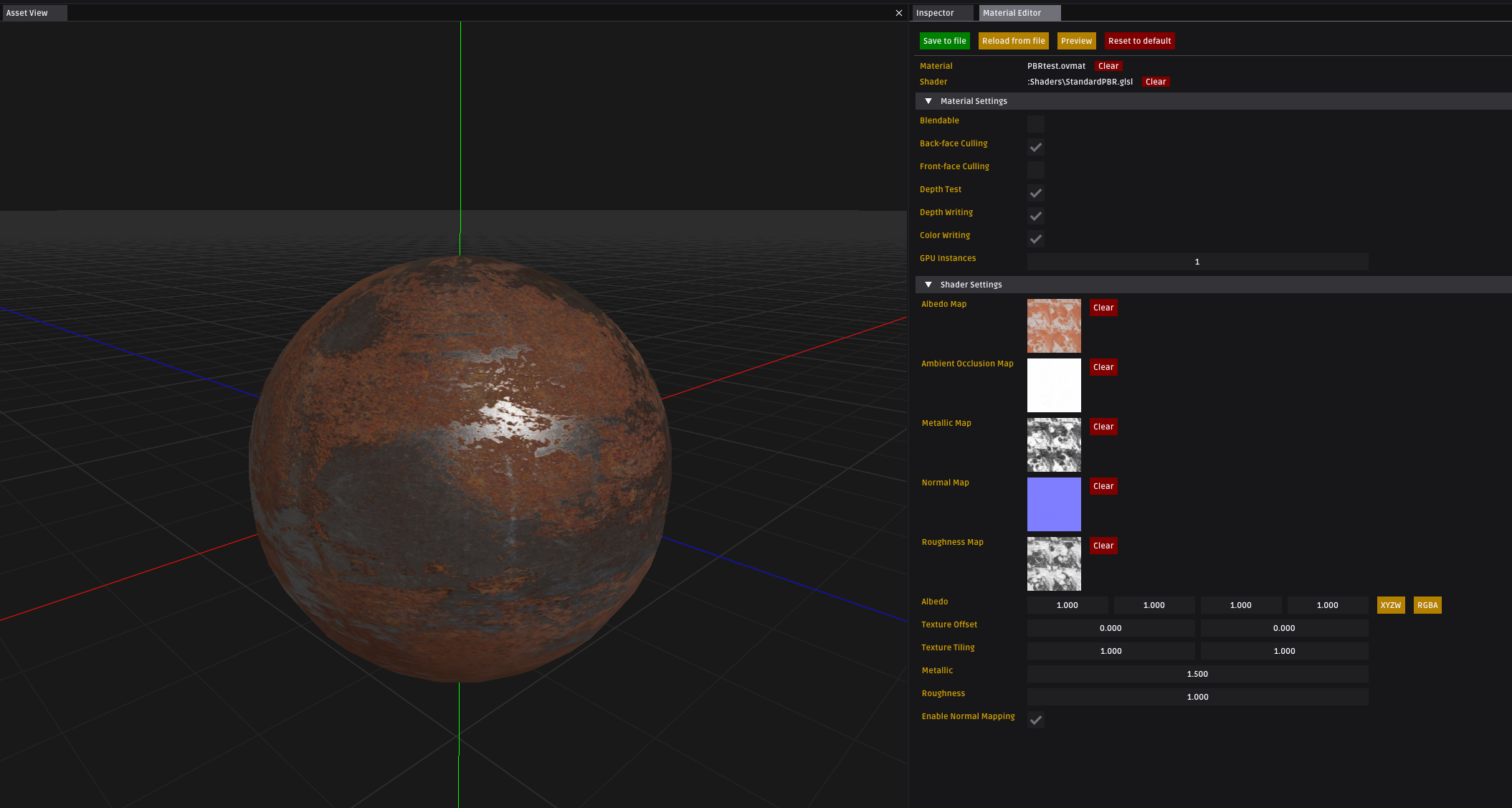
【Overload游戏引擎细节分析】PBR材质Shader---完结篇
PBR基于物理的渲染可以实现更加真实的效果,其Shader值得分析一下。但PBR需要较多的基础知识,不适合不会OpenGL的朋友。 一、PBR理论 PBR指基于物理的渲染,其理论较多,需要的基础知识也较多,我在这就不再写一遍了&…...
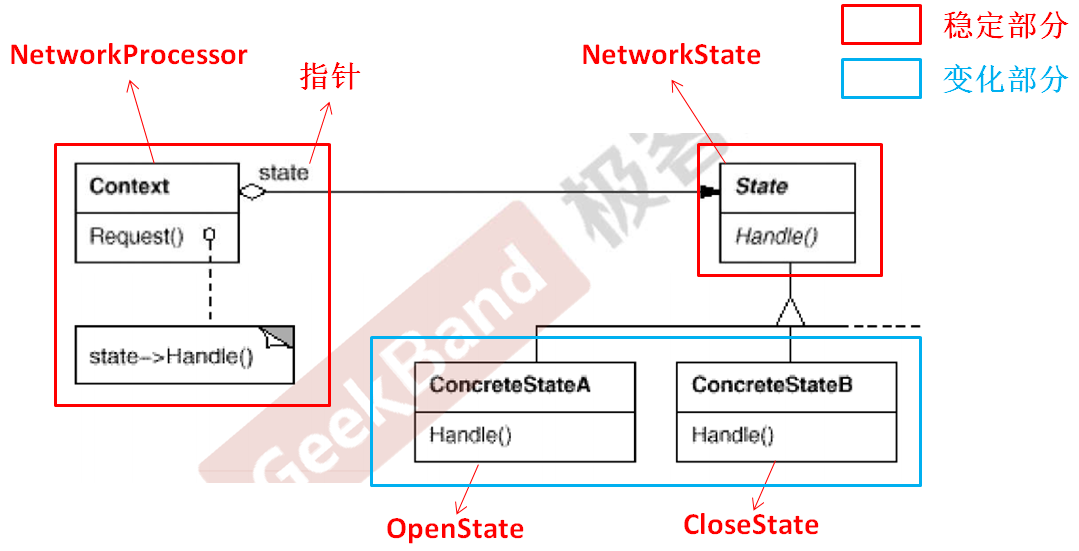
C++设计模式_18_State 状态模式
State和Memento被归为“状态变化”模式。 文章目录 1. “状态变化”模式1.1 典型模式 2. 动机 (Motivation)3. 代码演示State 状态模式3.1 常规方式3.2 State 状态模式 4. 模式定义5. 结构( Structure )6. 要点总结7. 其他参考 1. “状态变化”模式 在组件构建过程中…...
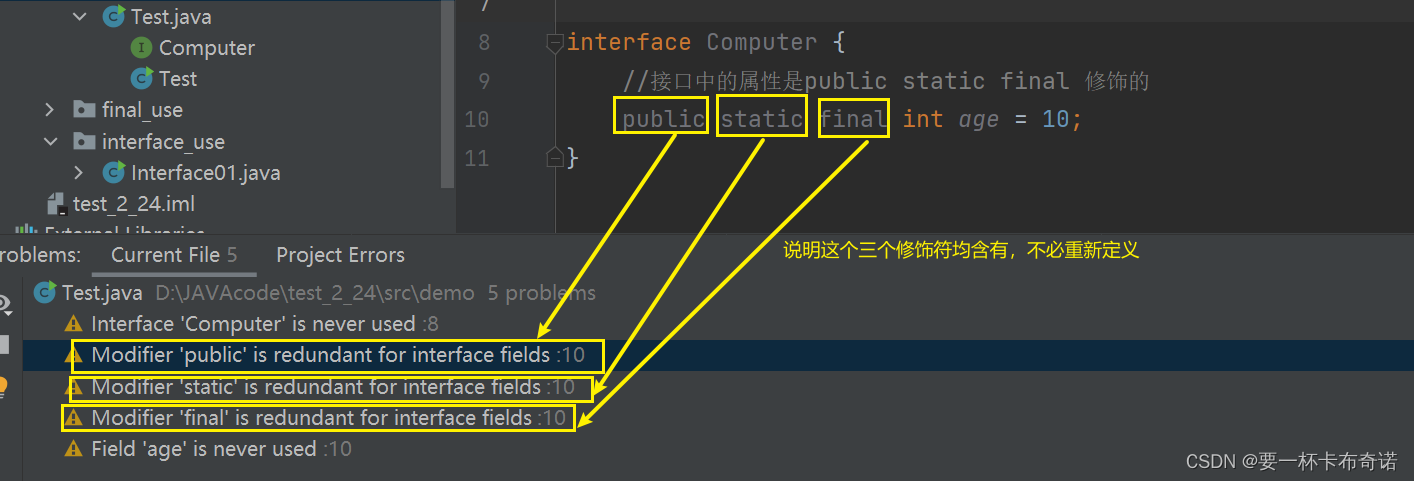
详解final, abstract, interface关键字
一.final关键字 1.final关键字介绍 ——final关键字可以去修饰类、方法、属性和局部变量 2.final关键字的作用 1)final修饰类,这个类不能被其他类继承 2)final修饰方法,方法不能被重写 3)final修饰属性,属…...

统计特殊四元组
题记: 给你一个 下标从 0 开始 的整数数组 nums ,返回满足下述条件的 不同 四元组 (a, b, c, d) 的 数目 : nums[a] nums[b] nums[c] nums[d] ,且a < b < c < d 示例 1: 输入: nums [1,2,3…...
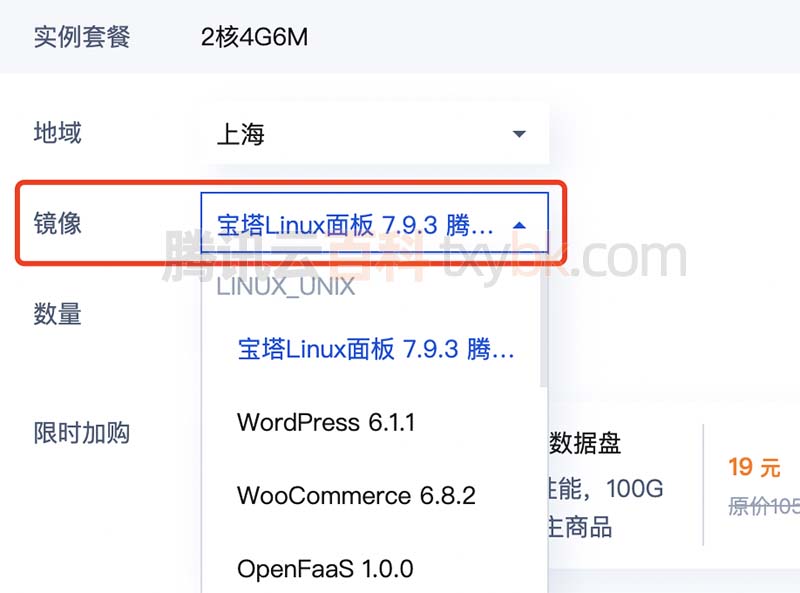
腾讯云轻量应用服务器“镜像”怎么选择合适?
腾讯云轻量应用服务器镜像怎么选择?如果是用来搭建网站可以选择宝塔Linux面板腾讯云专享版,镜像系统根据实际使用来选择,腾讯云百科txybk.com来详细说下腾讯云轻量应用服务器镜像的选择方法: 腾讯云轻量应用服务器镜像选择 轻量…...

Ruby模块和程序组织
和类一样,模块是一组方法和常量的集合。 和类不同,模块没有实例,取而代之的是可以将特殊模块的功能添加到一个类或者指定对象之中。 Class类是Module类的一个子类,因此每一个类对象也是一个模块对象 一、模块创建和基础应用 编写…...

14、SpringCloud -- WebSocket 实时通知用户
目录 实时通知用户需求:代码:前端:后端:WebSocket创建 websocket-server 服务添加依赖:配置 yml 和 启动类:前端:后端代码:注意:测试:总结:实时通知用户 需求: 用户订单秒杀成功之后,对用户进行秒杀成功通知。 弹出个提示框来提示。 代码: 前端:...
智能井盖传感器推荐,万宾科技助力城市信息化建设
随着科技产品更新换代进程加快,人工智能在人们日常生活之中逐渐普及开来,深入人们生活的方方面面,影响城市基础设施建设工程。例如在大街小巷之中的井盖作为城市基础建设的一个重要部分,一旦出现松动倾斜或凸起等异常问题…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
