C语言实现斐波那契数列的多种方法
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。对于解决此类问题方法有四,前两种对于初学者来说,应该可以思考研究明白,后两种就要求有一点点基础了,但是我相信,大家都可以学会的!!!
一、递归方法
完整代码展示如下:
#include <stdio.h>int fib(int n)
{if (n <= 1) {return n;} else {return fib(n - 1) + fib(n - 2);}
}int main()
{int n;printf("请输入一个整数: ");scanf("%d", &n);printf("斐波那契数列第%d项为: %d", n, fib(n));return 0;
}递归方法实现原理如下:
首先检查输入的n是否小于等于1。如果是,那么直接返回n,因为斐波那契数列的前两项就是0和1。
如果n大于1,那么函数会递归地调用自身两次,分别传入n-1和n-2作为参数。这是因为斐波那契数列的定义是每一项都是前两项的和。
最后,将这两个递归调用的结果相加,并返回结果。
结果展示:

二、迭代方法
完整代码展示如下:
#include <stdio.h>int fib(int n)
{if (n <= 1) {return n;}int a = 0, b = 1, temp;for (int i = 2; i <= n; i++) {temp = a + b;a = b;b = temp;}return b;
}int main()
{int n;printf("请输入一个整数: ");scanf("%d", &n);printf("斐波那契数列的第%d项为: %d", n, fib(n));return 0;
}迭代方法实现原理如下:
函数首先检查n是否小于等于1,如果是,则直接返回n。这是因为斐波那契数列的前两项是0和1。
如果n大于1,函数使用一个循环来计算斐波那契数列的第n项。在每次迭代中,它计算a和b的和,并将结果存储在临时变量temp中。然后,它将b的值赋给a,将temp的值赋给b。这样,a和b分别表示斐波那契数列的前两项和当前项。
循环继续进行,直到i等于n。最后,函数返回b的值,即斐波那契数列的第n项。
结果展示:
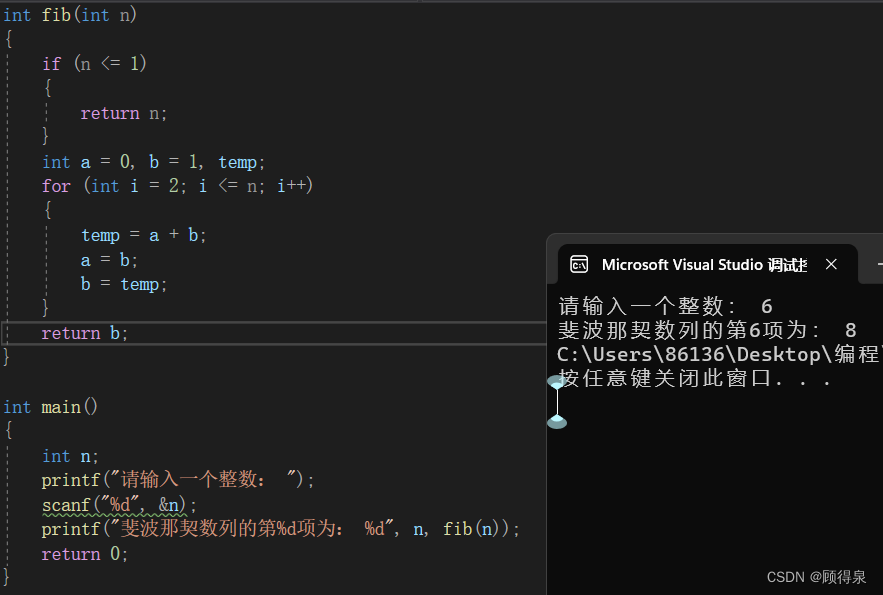
三、数组方法
完整代码展示如下:
#include <stdio.h>void fib(int n)
{int a[n];a[0] = 0;a[1] = 1;for (int i = 2; i < n; i++) {a[i] = a[i - 1] + a[i - 2];}for (int i = 0; i < n; i++) {printf("%d ", a[i]);}
}int main()
{int n;printf("请输入斐波那契数列的长度: ");scanf("%d", &n);fib(n);return 0;
}数组方法原理如下:
首先,代码声明了一个长度为n的整型数组a。然后,通过将数组的第一个元素和第二个元素分别赋值为0和1,初始化了斐波那契数列的前两个元素。
接着,使用一个for循环从索引2开始迭代到n-1。在每次迭代中,代码计算斐波那契数列的第i个元素,即前两个元素的和,并将其存储在数组a的相应位置。
最后,使用另一个for循环遍历数组a,并使用printf函数打印出每个元素的值。这样,你就可以看到斐波那契数列的前n个元素被打印出来了。
结果展示:

四、通项公式方法
要实现斐波那契数列通项公式方法,我们首先需要了解斐波那契数列的通项公式:
F(n) = (φ^n - (-φ)^-n) / sqrt(5)
其中,φ = (1 + sqrt(5)) / 2。
完整代码展示如下:
#include <stdio.h>
#include <math.h>double fibonacci(int n)
{double phi = (1 + sqrt(5)) / 2;return (pow(phi, n) - pow(-phi, -n)) / sqrt(5);
}int main()
{int n;printf("请输入要计算的斐波那契数列项数:");scanf("%d", &n);printf("第%d项斐波那契数列值为:%lf", n, fibonacci(n));return 0;
}通项公式方法原理如下:
函数内部首先定义了一个变量phi,它的值为(1 + sqrt(5)) / 2,这是斐波那契数列中相邻两项之比的近似值。
接着,函数使用公式(pow(phi, n) - pow(-phi, -n)) / sqrt(5)来计算斐波那契数列的第n项。其中,pow(x, y)表示求x的y次方,sqrt(x)表示求x的平方根。
最后,函数返回计算得到的斐波那契数列第n项的值。
结果展示:
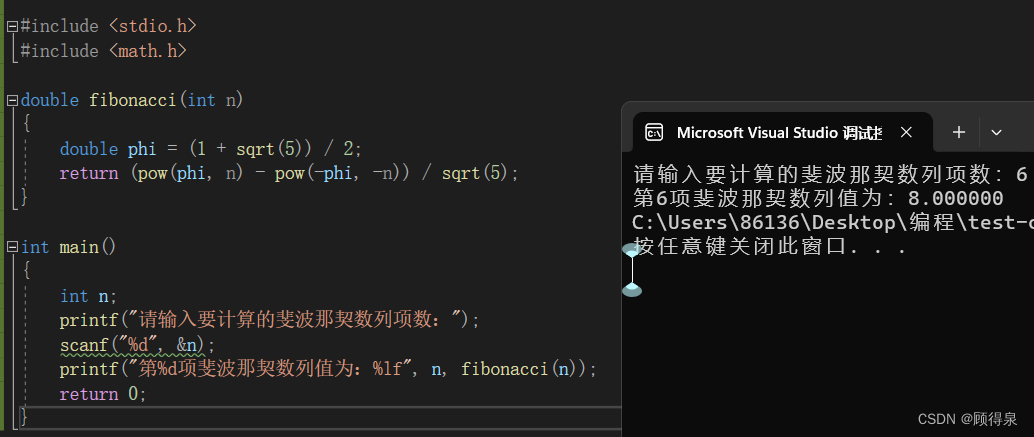
五、注意事项
第一种递归方法在计算较大的斐波那契数时可能会导致性能问题,因为它会重复计算许多相同的子问题。第三种方法使用了数组来存储已经计算过的斐波那契数列,可以提高效率。第四种方法使用了斐波那契数列的通项公式,可以直接计算出第n项的值,但是需要注意精度问题。
结语:以上就是相关斐波那契数列的解决方法了,希望对大家有所帮助。有什么问题欢迎大家留言~~~
相关文章:

C语言实现斐波那契数列的多种方法
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。对于解决此类问题方法有四,前两…...
一文解决:Swagger API 未授权访问漏洞问题
Swagger 是一个用于设计、构建、文档化和使用 RESTful 风格的 Web 服务的开源软件框架。它通过提供一个交互式文档页面,让开发者可以更方便地查看和测试 API 接口。然而,在一些情况下,未经授权的访问可能会导致安全漏洞。本文将介绍如何解决 …...
Elasticsearch下载安装,IK分词器、Kibana下载安装使用,elasticsearch使用演示
首先给出自己使用版本的网盘链接:自己的版本7.17.14 链接:https://pan.baidu.com/s/1FSlI9jNf1KRP-OmZlCkEZw 提取码:1234 一般情况下 Elastic Search(ES) 并不单独使用,例如主流的技术组合 ELK(…...

springboot自定义404页面
添加配置类 import java.io.File; import java.io.FileOutputStream; import java.io.IOException; import javax.servlet.Servlet; import org.apache.catalina.startup.Tomcat; import org.apache.catalina.valves.ErrorReportValve; import org.apache.coyote.UpgradeProtoc…...
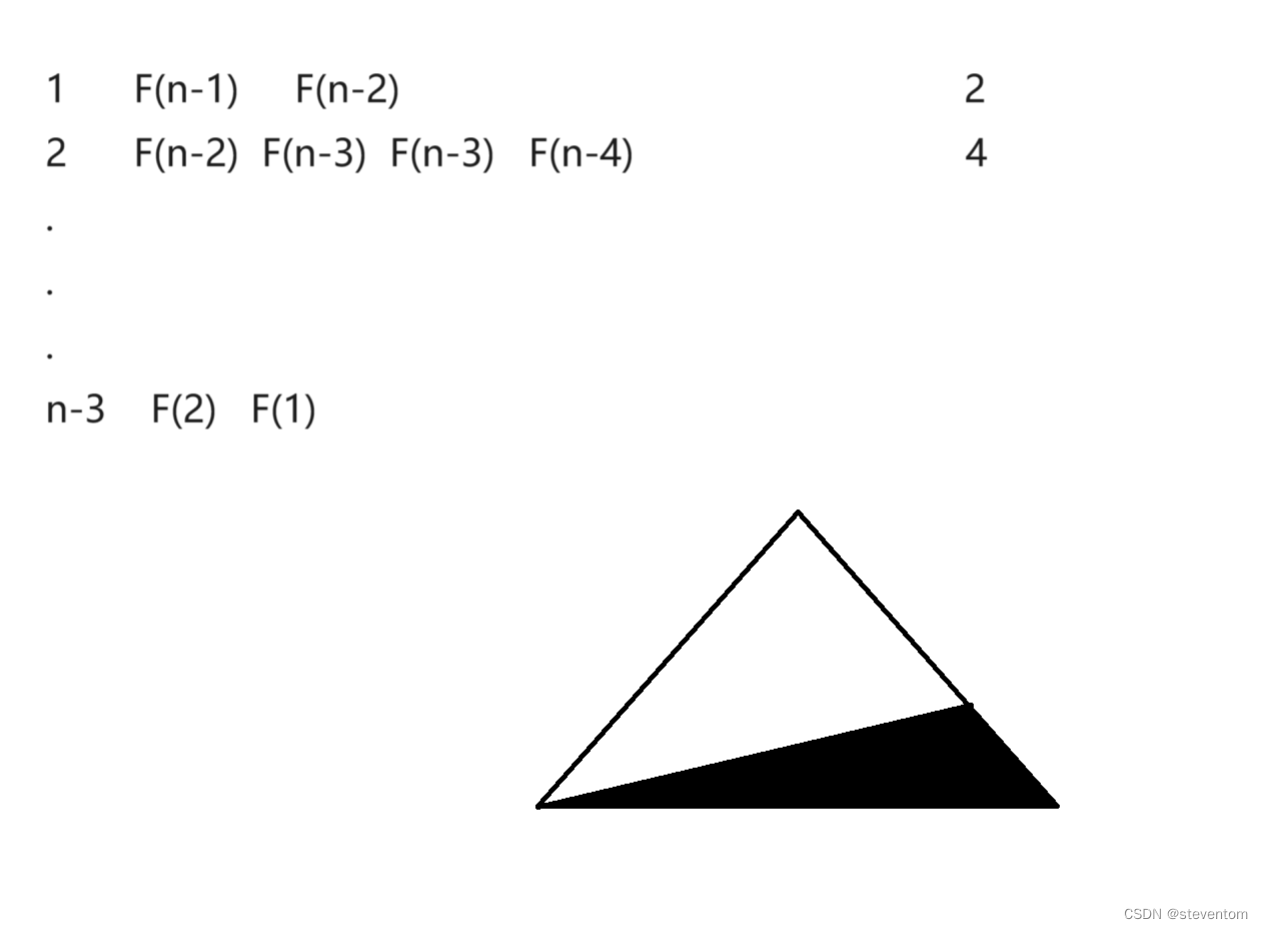
C/C++数据结构之时间复杂度和空间复杂度详细解析以及力扣刷题
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 数据结构初阶 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.前言 2.算法的…...

【需要理解】80 单词搜索
单词搜索 题解1 回溯(需要改变起点) 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内…...
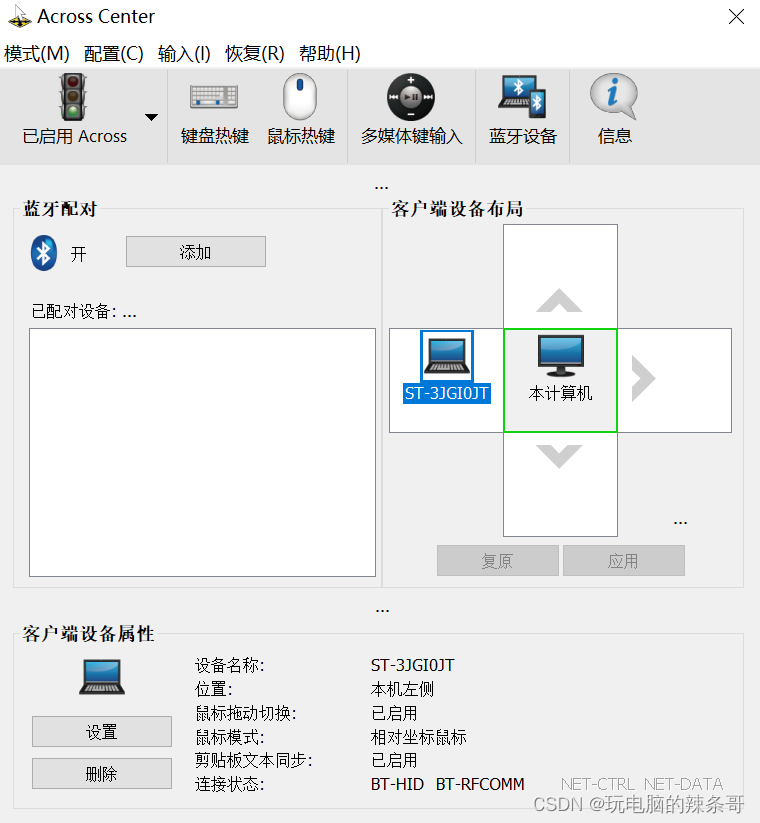
笔记本电脑的键盘鼠标如何共享控制另外一台电脑
环境: 联想E14 x2 Win10 across 2.0 问题描述: 笔记本电脑的键盘鼠标如何共享控制另外一台电脑 解决方案: 1.下载across软件,2台电脑都按装,一台设为服务端,一台客户端 2.把配对好设备拖到右边左侧…...

【计算机网络】(谢希仁第八版)第二章课后习题答案
第二章 1.物理层要解决哪些问题?物理层的主要特点是什么? 答:物理层要解决的主要问题: (1)物理层要尽可能地屏蔽掉物理设备和传输媒体,通信手段的不同,使数据链路层感觉不到这些差…...
笔记软件Notability mac中文版软件功能
Notability mac是一款帮助用户备注文件的得力工具,Notability Mac版可用于注释文稿、草拟想法、录制演讲、记录备注等。它将键入、手写、录音和照片结合在一起,便于您根据需要创建相应的备注。 Mac Notability mac中文版软件功能 将手写,照片…...
【C++的OpenCV】第十四课-OpenCV基础强化(三):Mat元素的访问之data和step属性
🎉🎉🎉 欢迎来到小白 p i a o 的学习空间! \color{red}{欢迎来到小白piao的学习空间!} 欢迎来到小白piao的学习空间!🎉🎉🎉 💖 C\Python所有的入门技术皆在 我…...
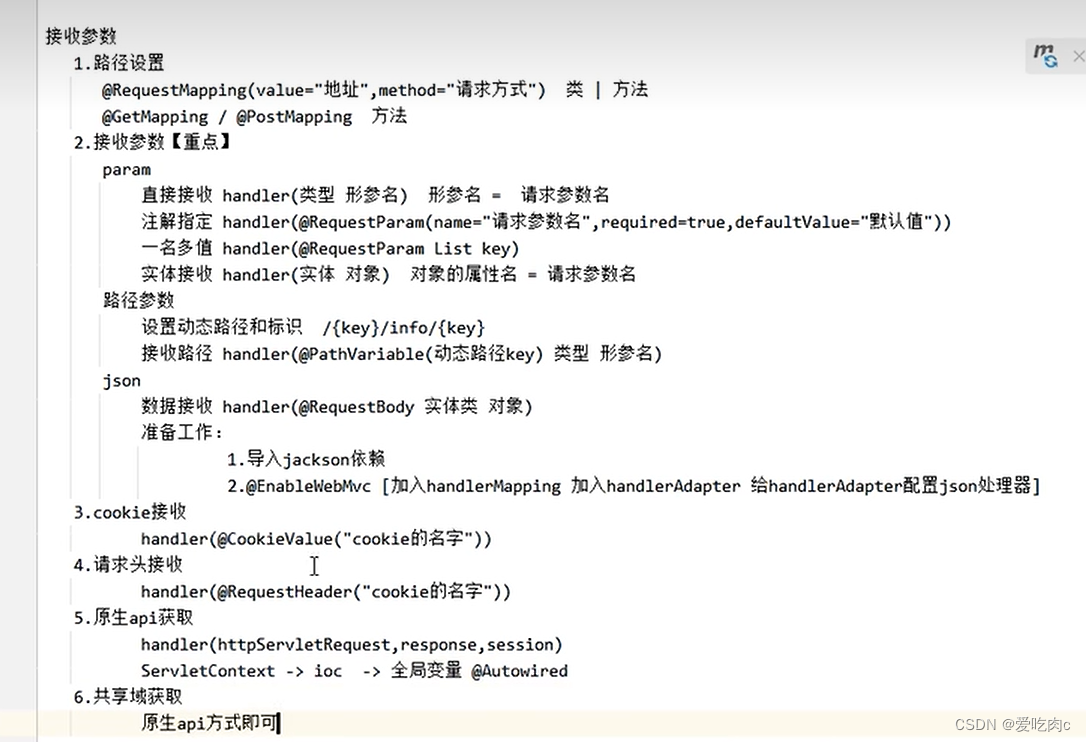
Springmvc 讲解(1)
文章目录 前言一、SpringMvc1、简介2、核心组件和调用流程2.1 涉及组件的理解 3、小案例快速体验3.1场景需求3.1.1 导入依赖3.1.2 controller声明3.1.3 核心配置类3.1.4 环境搭建3.1.6 配置tomcat3.1.7 测试 二、SpringMvc 接收参数1.路径设置注解2、param接收参数四种类型2.1 …...

超级英雄的导航之旅:动态路由和嵌套路由
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

发现个好玩的 Windows微信对话框换行
按住shift键按enter就是换行 直接按enter为发送...

Vue3最佳实践 第八章 ESLint 与 测试 ( Jest )
Jest 测试 Vue 组件 在前端项目开发过程中,有很多时候也会要进行测试工作。本文将重点介绍如何利用 JavaScript 测试框架 Jest 进行高效的测试。Jest 是由 FaceBook 开发的顶级测试框架之一,广受开发者们的欢迎和信赖。在接下来的内容中,我…...

【抓包分析】通过ChatGPT解密还原某软件登录算法实现绕过手机验证码登录
文章目录 🍋前言实现效果成品广告抓包分析一、定位加密文件二、编辑JS启用本地替换 利用Chatgpt进行代码转换获取计划任务id模拟数据请求最后 🍋前言 由于C站版权太多,所有的爬虫相关均为记录,不做深入! 今天发现gith…...
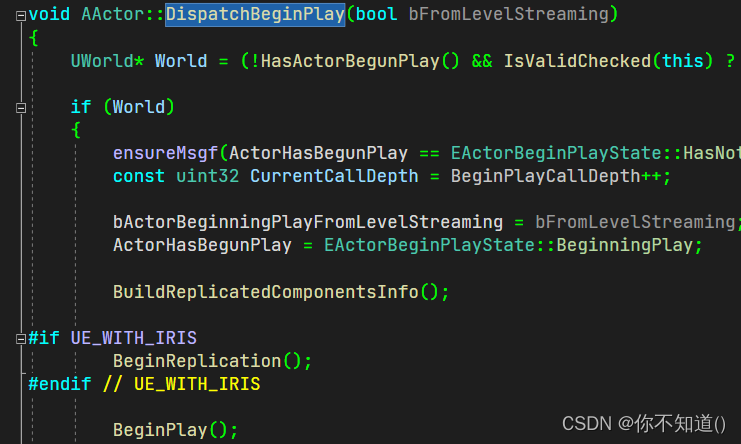
【UE】属性同步,源码详解一个勾选了Actor复制的Actor第一次被创建时经历了什么
本文参考https://zhuanlan.zhihu.com/p/640723352 准备工作 先准备一个勾选了复制的Actor,然后在游戏开始时Spawn这个Actor 源码过程详解 发送属性同步 在NetDriver的TickFlush中发送属性同步的数据 1、ServerReplicateActors_BuildConsiderList 去找到所有需…...

Spring中Bean的完整生命周期!(Bean实例化的流程,Spring后处理器,循环依赖解释及解决方法)附案例演示
Bean实例化的基本流程 加载xml配置文件,解析获取配置中的每个的信息,封装成一个个的BeanDefinition对象将BeanDefinition存储在一个名为beanDefinitionMap的Map<String,BeanDefinition>中ApplicationContext底层遍历beanDefinitionMap,…...

AcWing第 127 场周赛 - AcWing 5283. 牛棚入住+AcWing 5284. 构造矩阵 - 模拟+快速幂+数学
AcWing 5283. 牛棚入住 题目数据范围不大,直接暴力模拟即可 按照题目所说的意思即可。 #include <math.h> #include <stdio.h> #include <algorithm> #include <cstring> #include <iostream> using namespace std; const int N 1…...

2023-10-31 游戏开发-微信小游戏-文档记录
摘要: 2023-10-31 游戏开发-微信小游戏-文档记录 微信开发文档: 快速上手 | 微信开放文档 基础 | 微信开放文档 Cocos/Laya/Egret引擎适配 | 微信开放文档 cocos和微信平台相关文档: Cocos Creator 3.8 手册 - 发布到微信小游戏...

2023NOIP A层联测21-异或
给定一长度为 N N N 的由非负整数组成的数组 a a a,你需要进行一系列操作,每次操作选择一个区间 [ l , r ] [l,r] [l,r],将 a [ l , r ] a_{[l,r]} a[l,r] 异或上 w w w。你需要将 a i a_i ai 全部变为 0 0 0。 求最小操作次数。…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
