2023NOIP A层联测21-异或
给定一长度为 N N N 的由非负整数组成的数组 a a a,你需要进行一系列操作,每次操作选择一个区间 [ l , r ] [l,r] [l,r],将 a [ l , r ] a_{[l,r]} a[l,r] 异或上 w w w。你需要将 a i a_i ai 全部变为 0 0 0。
求最小操作次数。
N ≤ 17 N\le17 N≤17
考虑两个左端点相同的修改 [ l , r 1 ] , [ l , r 2 ] ( r 1 < r 2 ) [l,r_1],[l,r_2](r_1<r_2) [l,r1],[l,r2](r1<r2),可以把它拆成 [ l , r 1 ] [l,r_1] [l,r1] 和 [ r 1 + 1 , r 2 ] [r_1+1,r_2] [r1+1,r2],次数相同。所以没有两个区间左端点相同,反过来右端点也不相同。
将 a a a 序列异或差分得到 b b b,其中 b i = a i ⊕ a i − 1 b_i=a_i\oplus a_{i-1} bi=ai⊕ai−1,区间修改就变成双点修改(区间非后缀)或单点修改(区间为后缀)。最后同样要求 b b b 全为 0 0 0。
把 N N N 个数抽象成 N N N 个点,修改就是在两个点之间连边(如果是单点修改,就是自环),一组方案由几个连通块组成。先暂时不管 w w w 的取值,考虑什么情况时会存在一个 w w w。
一个连通块(大小为 x x x)中的边数只可能有两种情况, x − 1 x-1 x−1(一棵树), x x x(一棵树加自环)。我们的目标是让最后连通块的数全为 0 0 0。
考虑树的情况,发现有解当且仅当连通块内的数异或和为 0 0 0。下证之。
必要性:每次操作都是双点修改,整个连通块内的异或和不变,而最后要求异或和为 0 0 0,那么一开始也必须是 0 0 0。
充分性:考虑把这些数按编号顺序排成一排,从前往后做操作,每次操作都把最前面的消掉了(变成 0 0 0),而最后应得到全 0 0 0 的序列,所以异或和必为 0 0 0。
对于有自环的情况,自环的操作把那个点改成一个适当的值,让除去自环的这棵树的异或和为 0 0 0,所以这无论如何都有解。
发现答案就是 N N N 减去异或和为 0 0 0 的子序列个数。现在目标是最大化这样的子序列个数。
可以用状压 DP 求解,先枚举状态 i i i,再枚举它的子集 s s s,若 s s s 的异或和为 0 0 0, d p i ← max ( d p i , d p i ⊕ s ) dp_i\gets\max(dp_i,dp_{i\oplus s}) dpi←max(dpi,dpi⊕s)。时间复杂度 O ( 3 n ) O(3^n) O(3n)。
注意要预处理出每个子集的异或和。
具体实现参照代码。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=(1<<17)+1;
int n,dp[N];
ll a[20],b[20],sum[N];
int main()
{freopen("xor.in","r",stdin);freopen("xor.out","w",stdout);scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%lld",&a[i]),b[i]=a[i]^a[i-1];int N=1<<n;for(int i=0;i<N;i++){for(int j=0;j<n;j++){if(i>>j&1){sum[i]^=b[j+1];}}}for(int i=0;i<N;i++){for(int s=i;s;s=(s-1)&i){if(!sum[s]) dp[i]=max(dp[i],dp[i^s]+1);}}printf("%d",n-dp[N-1]);
}
相关文章:

2023NOIP A层联测21-异或
给定一长度为 N N N 的由非负整数组成的数组 a a a,你需要进行一系列操作,每次操作选择一个区间 [ l , r ] [l,r] [l,r],将 a [ l , r ] a_{[l,r]} a[l,r] 异或上 w w w。你需要将 a i a_i ai 全部变为 0 0 0。 求最小操作次数。…...

分布式存储系统Ceph应用组件介绍
1、 无中心架构分布式存储Ceph Ceph是一套开源的分布式存储系统。具有可靠性高,性能优良,可伸缩,与HDFS不同的地方在于,该架构中没有中心节点。 Ceph优点在于它不单单是存储,同时还充分利用了存储节点上的计算能…...
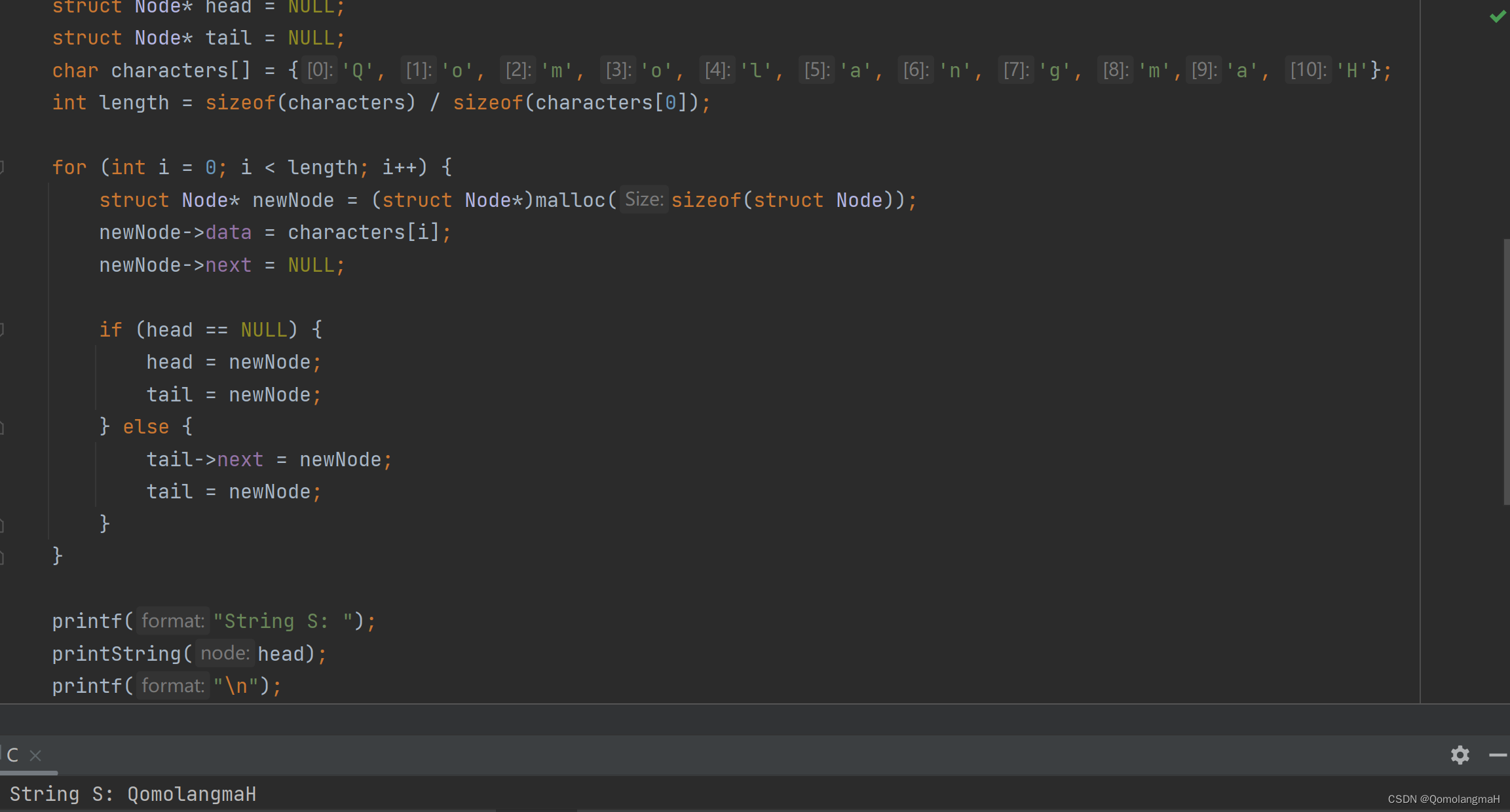
【数据结构】数组和字符串(十一):字符串的定义与存储(顺序存储、链式存储及其C语言实现)
文章目录 4.3 字符串4.3.1 字符串的定义与存储1. 顺序存储2. 链式存储3. C语言实现顺序存储4. C语言实现链式存储代码优化 4.3 字符串 字符串(String)是由零个或多个字符(char)顺序排列组成的有限序列,简称为串。例如 “good morning”就是由12个字符构成的一个字符…...

zk-Bench:SNARKs性能对比评估工具
1. 引言 JENS ERNSTBERGER等人2023年论文《zk-Bench: A Toolset for Comparative Evaluation and Performance Benchmarking of SNARKs》。 zk-Bench,定位为: 定位为首个公钥密码学性能评估基准测试框架和工具,重点关注通用ZKP系统的实测评…...
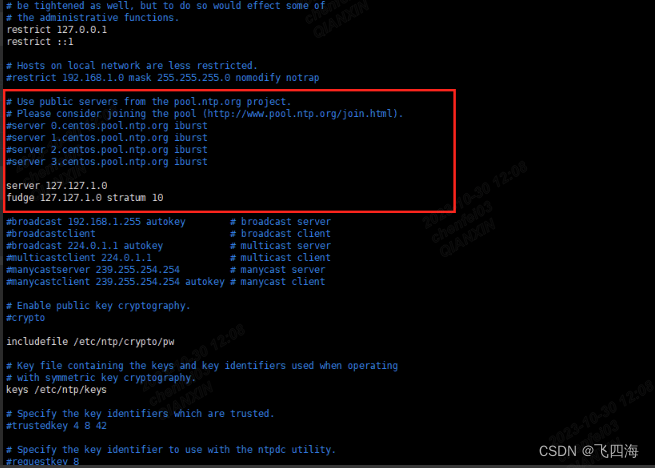
【Linux】NTP服务器配置、时间修改
查看当前系统时间date修改当前系统时间date -s "2018-2-22 19:10:30"查看硬件时间hwclock --show修改硬件时间hwclock --set --date "2018-2-22 19:10:30"同步系统时间和硬件时间hwclock --hctosys保存时钟clock –w1.设置NTP Server服务检查系统是否安装n…...
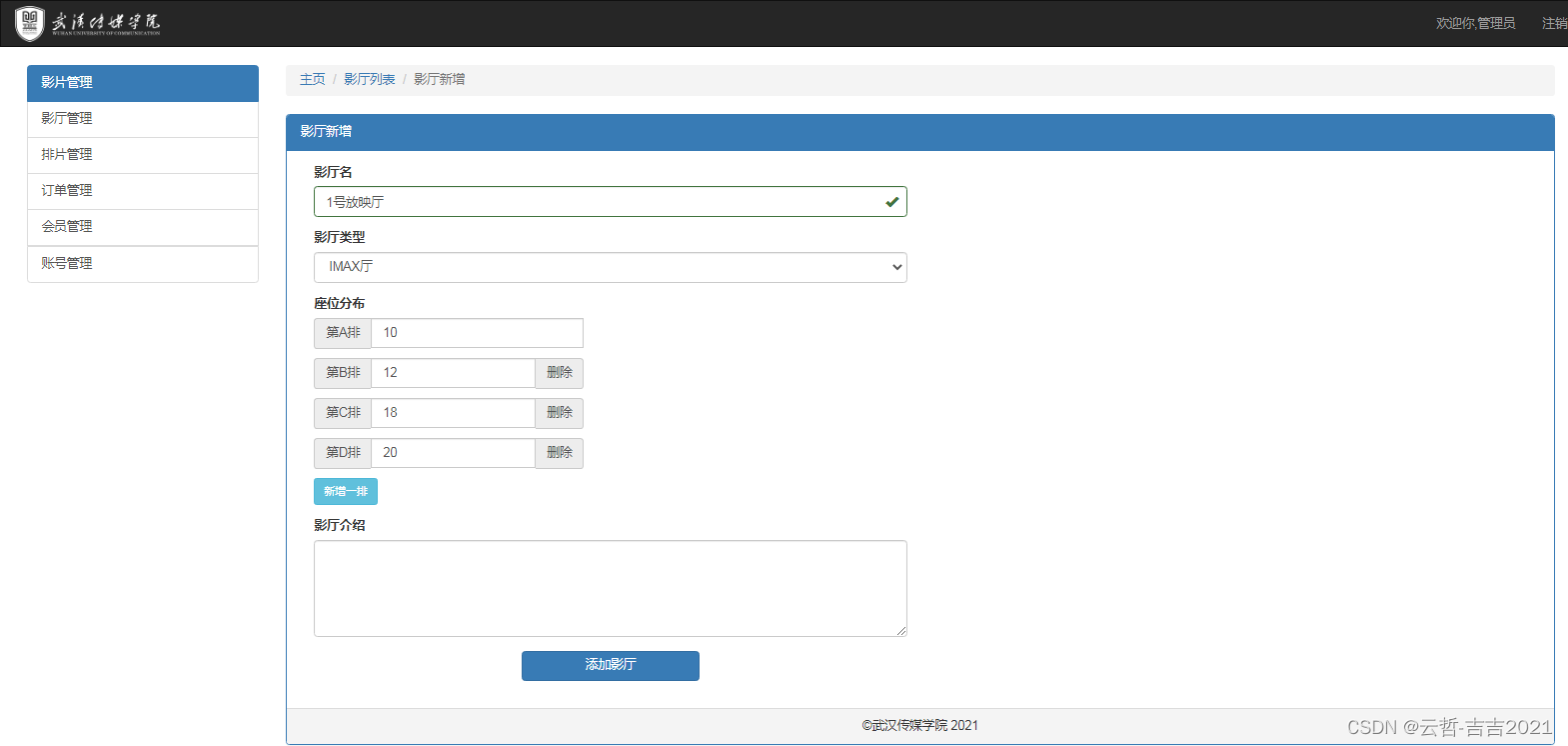
毕业设计基于SpringMVC+Mybatis+Bootstrap的电影院管理系统源码+数据库
<<电影院管理系统>> 电影院管理系统:SpringMVCJSPTomcatMybatisBootstrapJqueryAnimateCSSLayerJS 项目部署:该项目是IDEA版本,Maven项目 前端依赖: Bootstrap-3.4.1Animate.css- 4.1.1Jquery-3.6.0Layer-v3.5.1B…...
浏览器返回上一页的失效问题)
vantUI(Tabbar标签页)浏览器返回上一页的失效问题
在开发中遇到这样一个问题,由页面1切换到页面2,再点击浏览器的回退,无法回退到页面1。 开始以为是路由配置的有问题,但是子页面可以正常回退,因为replace只是替换路由,而不会往history栈中记录路由&#x…...
)
【算法】Prim算法(求最小生成树)
题目 给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。 求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。 给定一张边带权的无向图 G(V,E),其中 V 表示图中点的集合,E…...

go语言,yaml实现简单的workflow工作流
目录 1.创建一个yaml文件,名字可以是student.yaml 2.创建go文件测试 3.执行结果 本文章内容,只是一个简单的案例,但足够映射到一个大的项目中。 工作流作用:工作流的作用就是通过yaml配置文件,将关于本工作流的一个…...

BaiduMallServcie
说明 本文档指导业务开发步骤 BaiduMallServcie 说明一. 登录业务1.1 数据库设计1.1.1 管理员表1.1.2 角色表1.1.3 关联表 管理员表与角色表关联1.1.4 权限表1.1.5 关联表 角色表与权限表关联1.1.6 管理员登录日志表1.1.7 查询权限示例1.2 添加用户一. 登录业务 1.1 数据库设…...
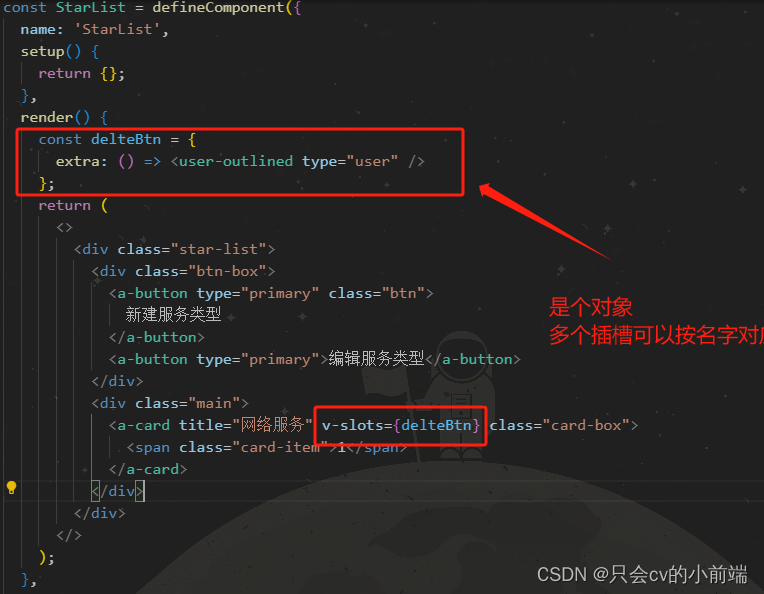
vue3+jsx+antd的插槽写法之一
如果在jsx里面直接这样按照官方的写法是会报错的 正确写法是:...

Shell 学习之 if 命令
1. 执行流程 在 Shell 脚本中,if 是一个 控制流语句,用于进行条件判断,根据条件的结果执行相应的操作。 # 首先,Shell 会检查表达式 condition 返回的 boolean 值。 # 如果 condition 的值为真,则执行 then 代码块&a…...

android 同步 服务器 时间
要将 Android 设备与服务器同步时间,可以通过以下两种方式实现: NTP 协议同步时间 NTP(Network Time Protocol)是一种网络协议,用于同步计算机的时间。Android 设备可以使用 NTP 协议来同步服务器时间。 Android 应…...
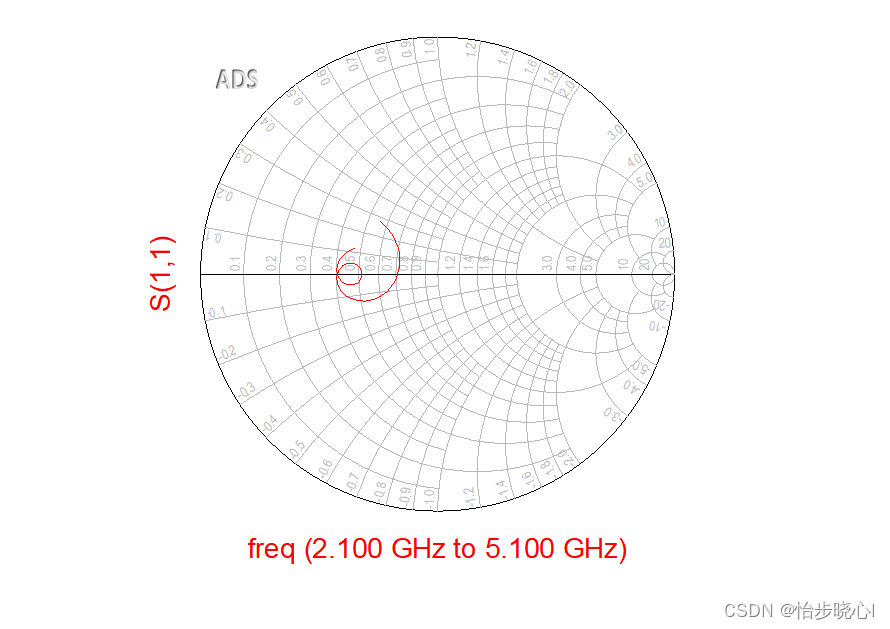
10、电路综合-基于简化实频的宽带匹配电路设计方法
10、电路综合-基于简化实频的宽带匹配电路设计方法 网络综合和简化实频理论学习概述中的1-9介绍了SRFT的一些基本概念和实验方法,终于走到了SRFT的另一个究极用途,宽带匹配电路的设计。 1、之前的一些回顾与总结 之前也给出了一些电路综合的案例&…...
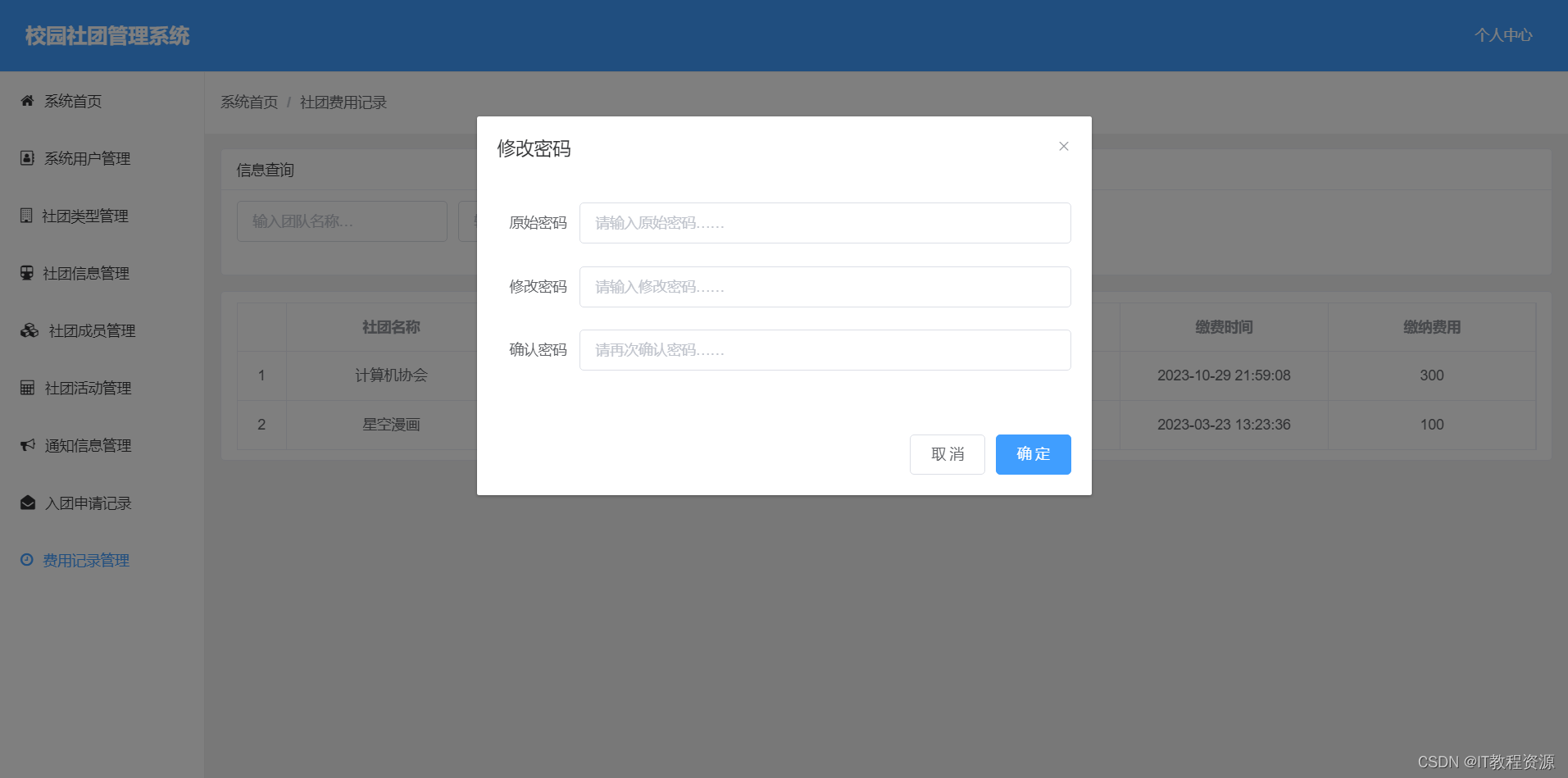
N-130基于springboot,vue校园社团管理系统
开发工具:IDEA 服务器:Tomcat9.0, jdk1.8 项目构建:maven 数据库:mysql5.7 系统分前后台,项目采用前后端分离 前端技术:vueelementUI 服务端技术:springbootmybatis-plus 本系…...
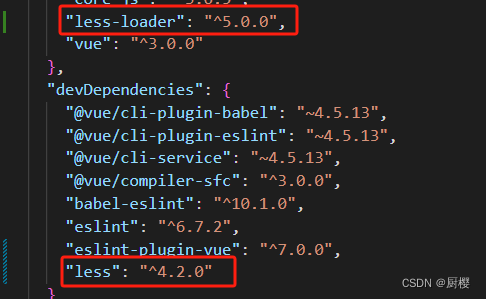
Syntax Error: TypeError: this.getOptions is not a function的解决(Vue)
报错信息: TypeError: this.getOptions is not a function 这个是在运行项目是遇到的问题 这个报错是类型错误,this.getOptions 不是一个函数 。这个错误一般就是less-loader库里的错误。 主要是less-loader版本太高,不兼容this.getOptions…...

使用 kube-downscaler 降低Kubernetes集群成本
新钛云服已累计为您分享772篇技术干货 介绍 Kube-downscaler 是一款开源工具,允许用户定义 Kubernetes 中 pod 资源自动缩减的时间。这有助于通过减少非高峰时段的资源使用量来降低基础设施成本。 在本文中,我们将详细介绍 kube-downscaler 的功能、安装…...

LeetCode热题100——哈希表
哈希表 1.两数之和2.字母异位词分组3.最长连续序列 1.两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。可以按任意顺序返回答案。 // 题解思路:使用哈…...

Kubeadm
目录 绪论:实验步骤 1、环境准备 2、所有节点安装docker 3、所有节点安装kubeadm,kubelet和kubectl 4、部署K8S集群 5、部署 Dashboard 6、安装Harbor私有仓库 master(2C/4G,cpu核心数要求大于2) 192.168.…...
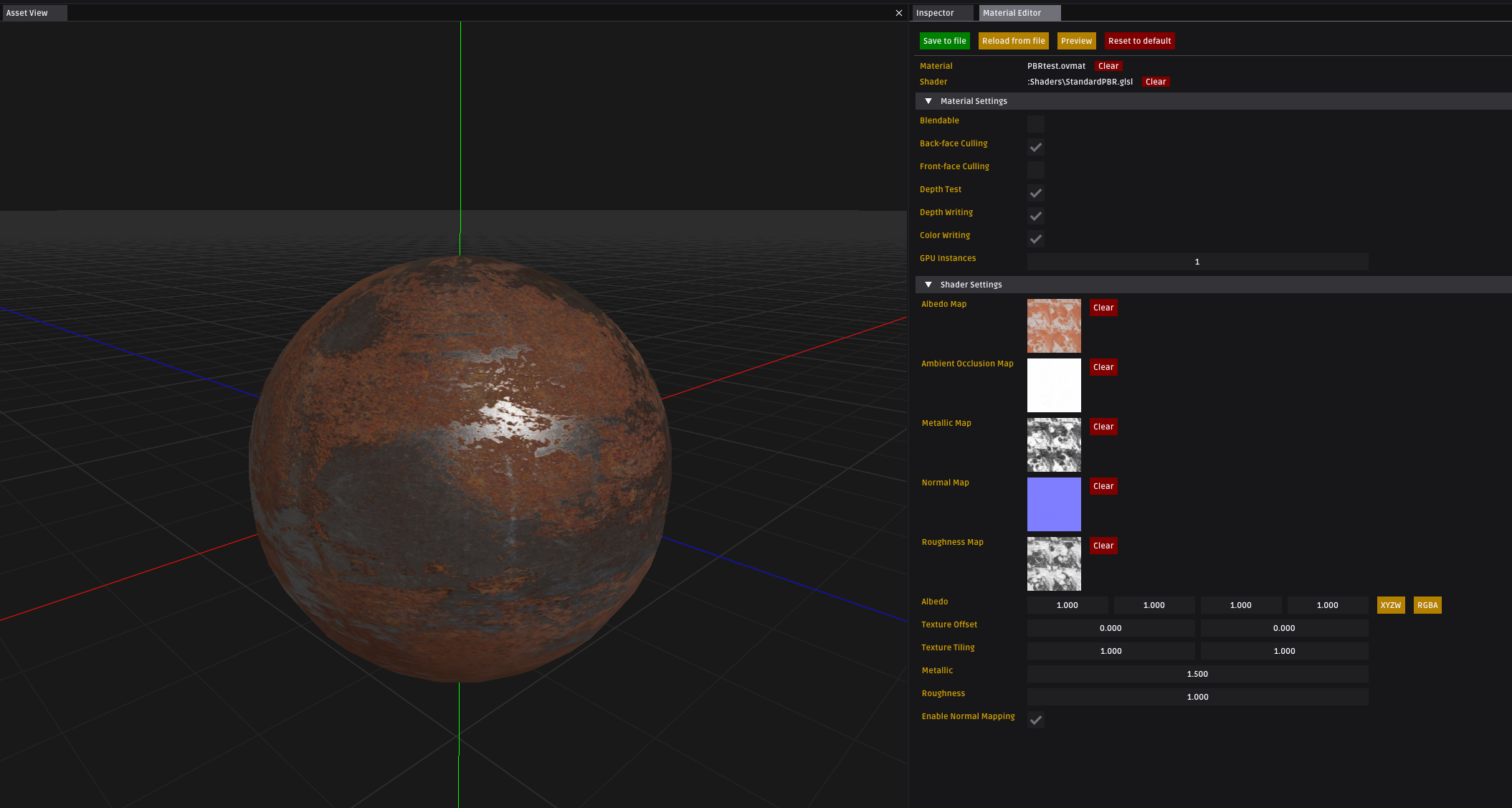
【Overload游戏引擎细节分析】PBR材质Shader---完结篇
PBR基于物理的渲染可以实现更加真实的效果,其Shader值得分析一下。但PBR需要较多的基础知识,不适合不会OpenGL的朋友。 一、PBR理论 PBR指基于物理的渲染,其理论较多,需要的基础知识也较多,我在这就不再写一遍了&…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
