AcWing89. a^b
题目
求 a a a 的 b b b 次方对 p p p 取模的值。
输入格式
三个整数 a , b , p , a,b,p, a,b,p, 在同一行用空格隔开。
输出格式
输出一个整数,表示 a^b mod p 的值。
数据范围
0 ≤ a , b ≤ 1 0 9 0≤a,b≤10^9 0≤a,b≤109
1 ≤ p ≤ 1 0 9 1≤p≤10^9 1≤p≤109
输入样例
3 2 7
输出样例
2
思路
快速幂。
任何一个整数都可以唯一表示为若干指数不重复的 2 的次幂的和。即是说如果 b b b 在二进制表示下 k k k 位,其中第 i ( 0 ≤ i ≤ k ) i(0 \le i \le k) i(0≤i≤k) 位的数字是 c i c_i ci,那么:
b = c k − 1 2 k − 1 + c k − 2 2 k − 2 + . . . + c 0 2 0 b = c_{k-1}2^{k-1} + c_{k-2}2^{k-2} + ... + c_0 2^0 b=ck−12k−1+ck−22k−2+...+c020
于是
a b = a c k − 1 × 2 k − 1 ∗ a c k − 2 × 2 k − 2 ∗ . . . ∗ a c 0 × 2 0 a ^b = a^{c_{k-1}\times2^{k-1}} * a^{c_{k-2} \times 2^{k-2}} * ... * a^{c_0 \times 2^0} ab=ack−1×2k−1∗ack−2×2k−2∗...∗ac0×20
因为 k = ⌈ l o g 2 ( b + 1 ) ⌉ k = \lceil log_2(b+1) \rceil k=⌈log2(b+1)⌉,所以上式乘积项的数量不多于 k = ⌈ l o g 2 ( b + 1 ) ⌉ k = \lceil log_2(b+1) \rceil k=⌈log2(b+1)⌉ 个。又因为:
a 2 i = ( a 2 i − 1 ) 2 a^{2^i} = (a^{2^{i-1}})^2 a2i=(a2i−1)2
所以可以通过 k k k 次递归求出每个乘积项,当 c i = 1 c_i = 1 ci=1 时,将该乘积项累积到答案中。KaTeX parse error: Expected 'EOF', got '&' at position 3: b &̲ 1 运算可以取出 b b b 在二进制表示下的最低位,而 b > > 1 b >> 1 b>>1 运算可以舍去最低位,在递推过程中将二者集合,就可以遍历 b b b 在二进制表示下的所有数位 c i c_i ci。
整个算法的时间复杂度为 O ( l o g 2 b ) O(log_2b) O(log2b)。
代码
#include <cstdio>using namespace std;int main() {int a, b, p;scanf("%d%d%d", &a, &b, &p);int ans = 1 % p;while (b) {if (b & 1) ans = (long long)ans * a % p;b >>= 1;a = (long long)a * a % p;}printf("%d\n", ans);return 0;
}
注意
在 C++ 语言中,两个数值执行算术运算时,以参与运算的最高数值类型为基准,与保存结果的变量类型无关。换言之,虽然两个 32 位整数的乘积可能超过 int 类型的表示范围,但是 CPU 只会用 1 个 32 位寄存器保存结果,造成越界现象。因此,必须把其中一个数强制转换成 64 位整数类型 long long 参与运算,从而得到正确的结果。最终对 p p p 取模以后,执行赋值操作时,该结果会被隐式转换成 int 存回 ans 中。
相关文章:

AcWing89. a^b
题目 求 a a a 的 b b b 次方对 p p p 取模的值。 输入格式 三个整数 a , b , p , a,b,p, a,b,p, 在同一行用空格隔开。 输出格式 输出一个整数,表示 a^b mod p 的值。 数据范围 0 ≤ a , b ≤ 1 0 9 0≤a,b≤10^9 0≤a,b≤109 1 ≤ p ≤ 1 0 9 1≤p≤10^…...
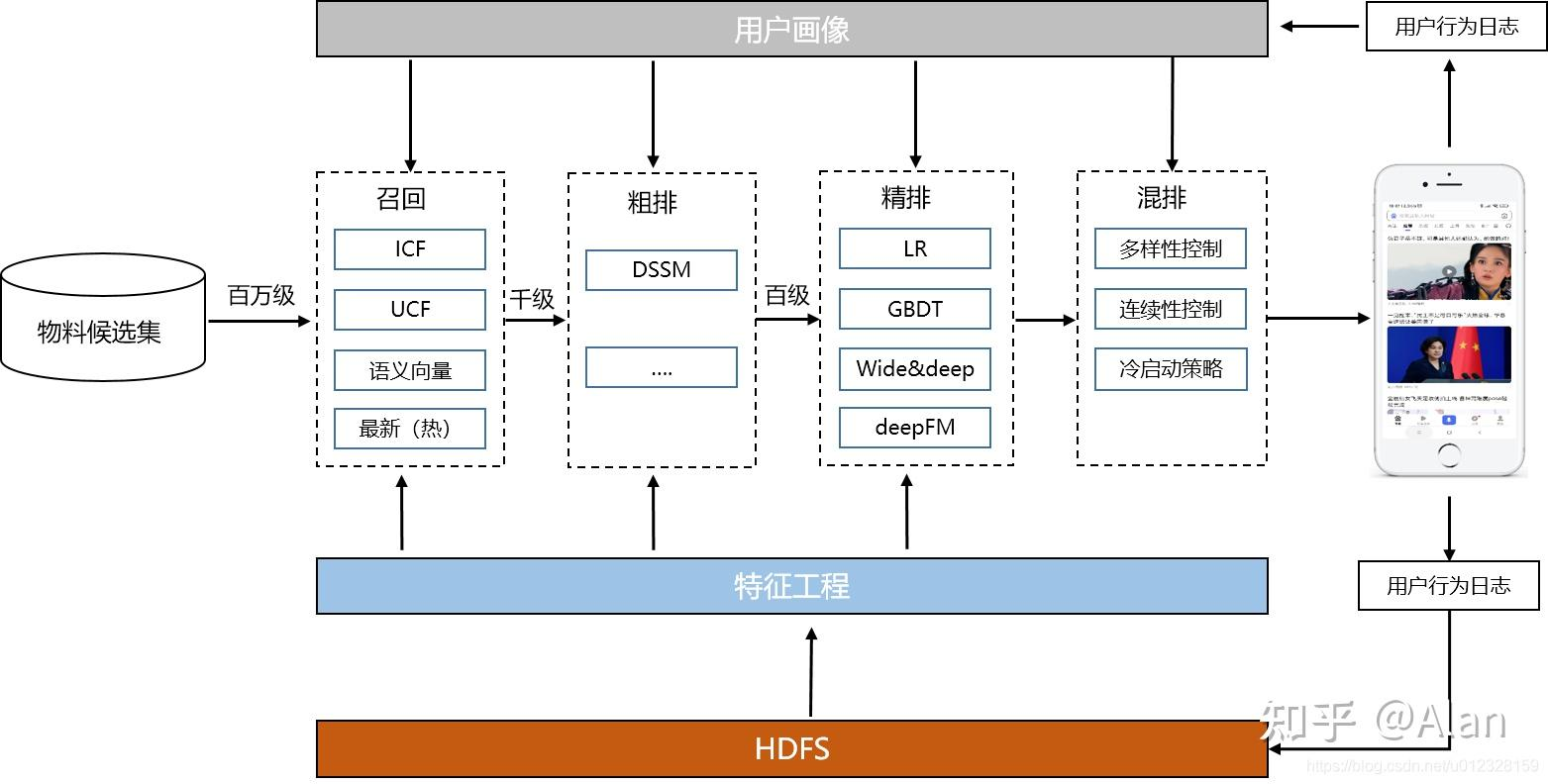
【推荐系统】推荐算法:冷启动-召回-粗排-精排-重排 解读
【推荐系统】推荐算法:冷启动-召回-粗排-精排-重排 解读 文章目录 【推荐系统】推荐算法:冷启动-召回-粗排-精排-重排 解读1. 介绍2. 冷启动2.1 用户冷启动2.1.1 利用用户注册信息冷启动2.1.2 好物推荐冷启动2.1.3 问题启发式冷启动2.1.4 社交冷启动2.1.…...

NB-IOT的粮库挡粮门异动监测装置
一种基于NBIOT的粮库挡粮门异动监测装置,包括若干个NBIOT开门监测装置,物联网后台管理系统,NBIOT低功耗广域网络和用户访问终端;各个NBIOT开门监测装置通过NBIOT低功耗广域网络与物联网后台管理系统连接,物联网后台管理系统与用户访问终端连接.NBIOT开门监测装置能够对粮库挡粮…...
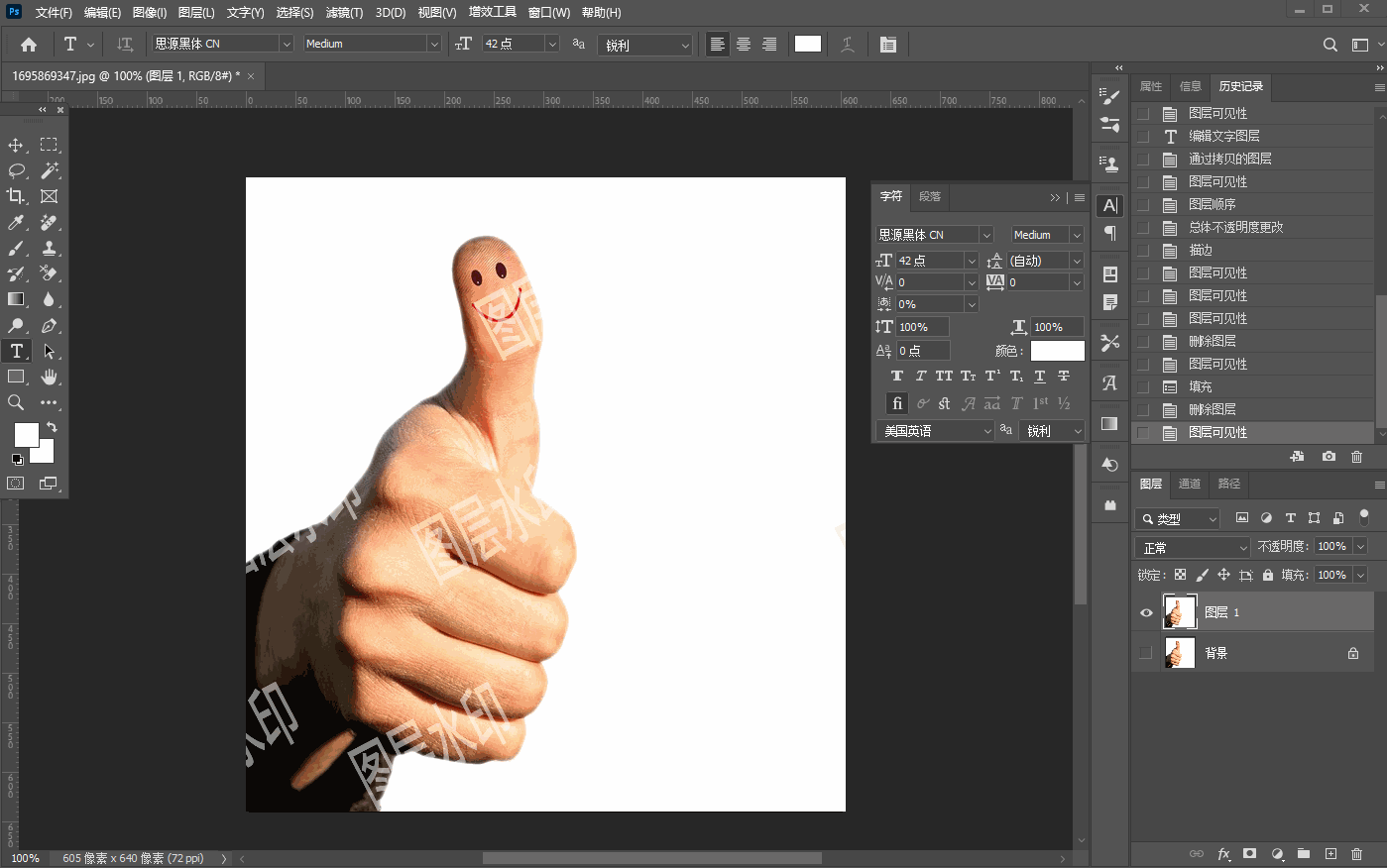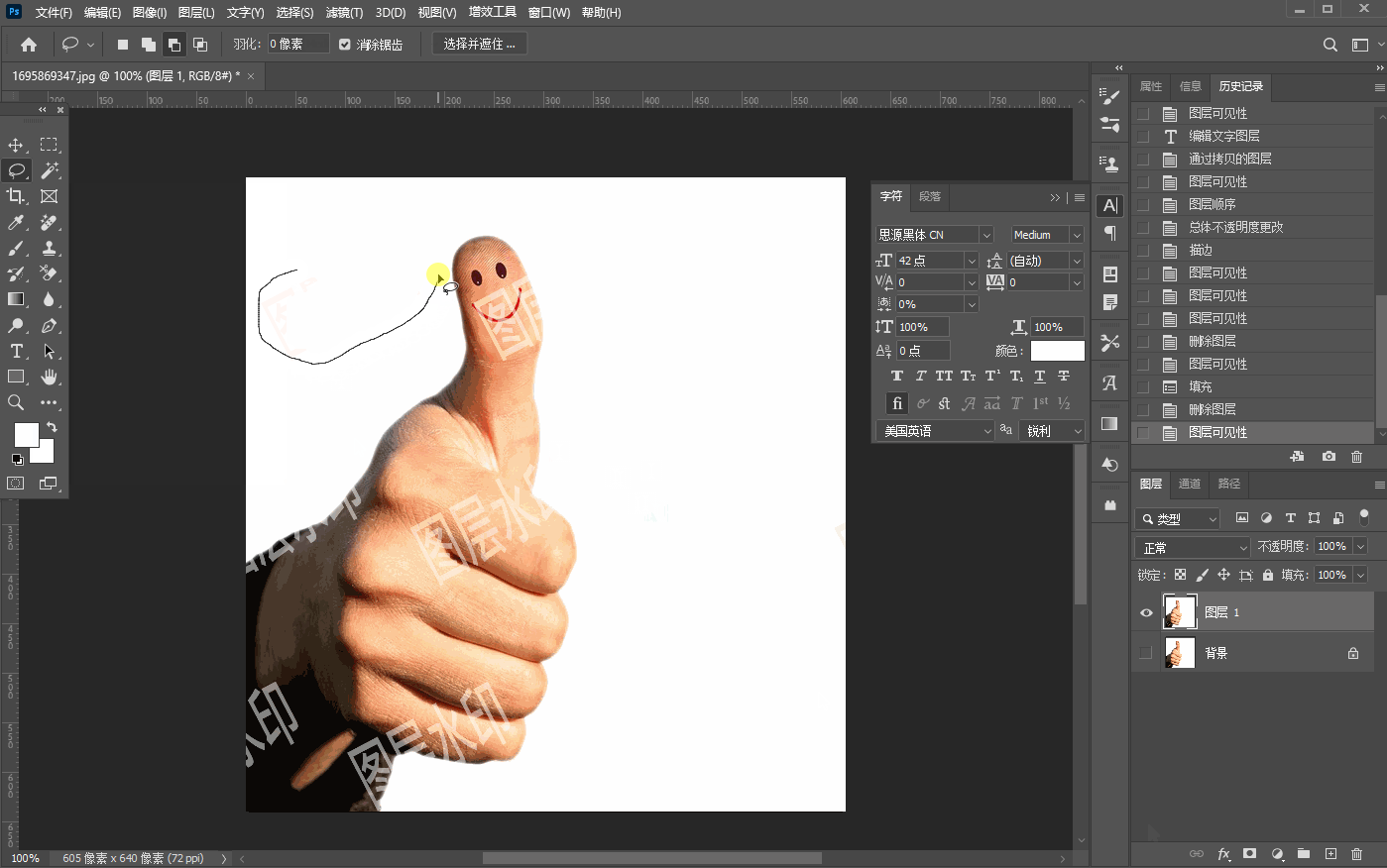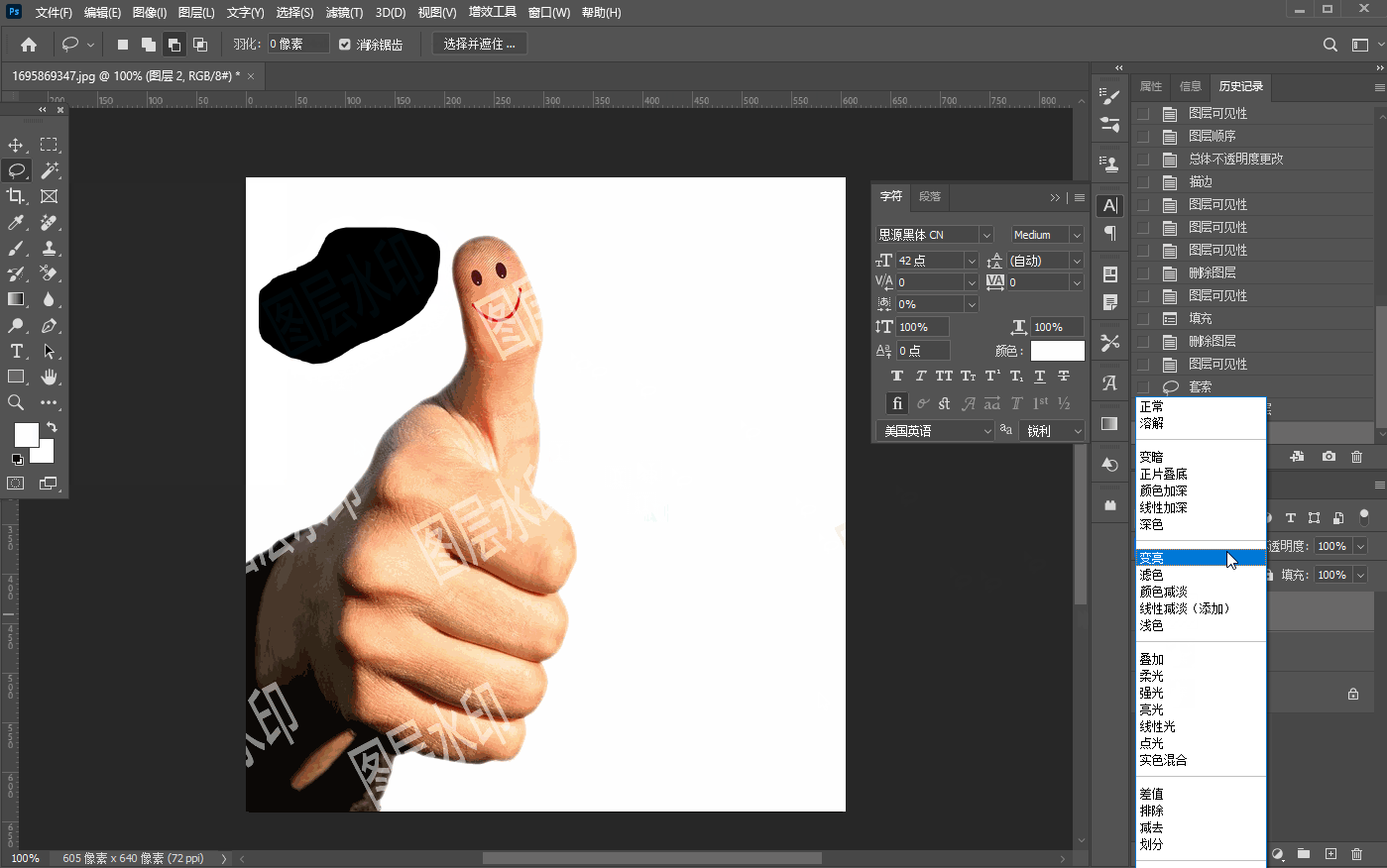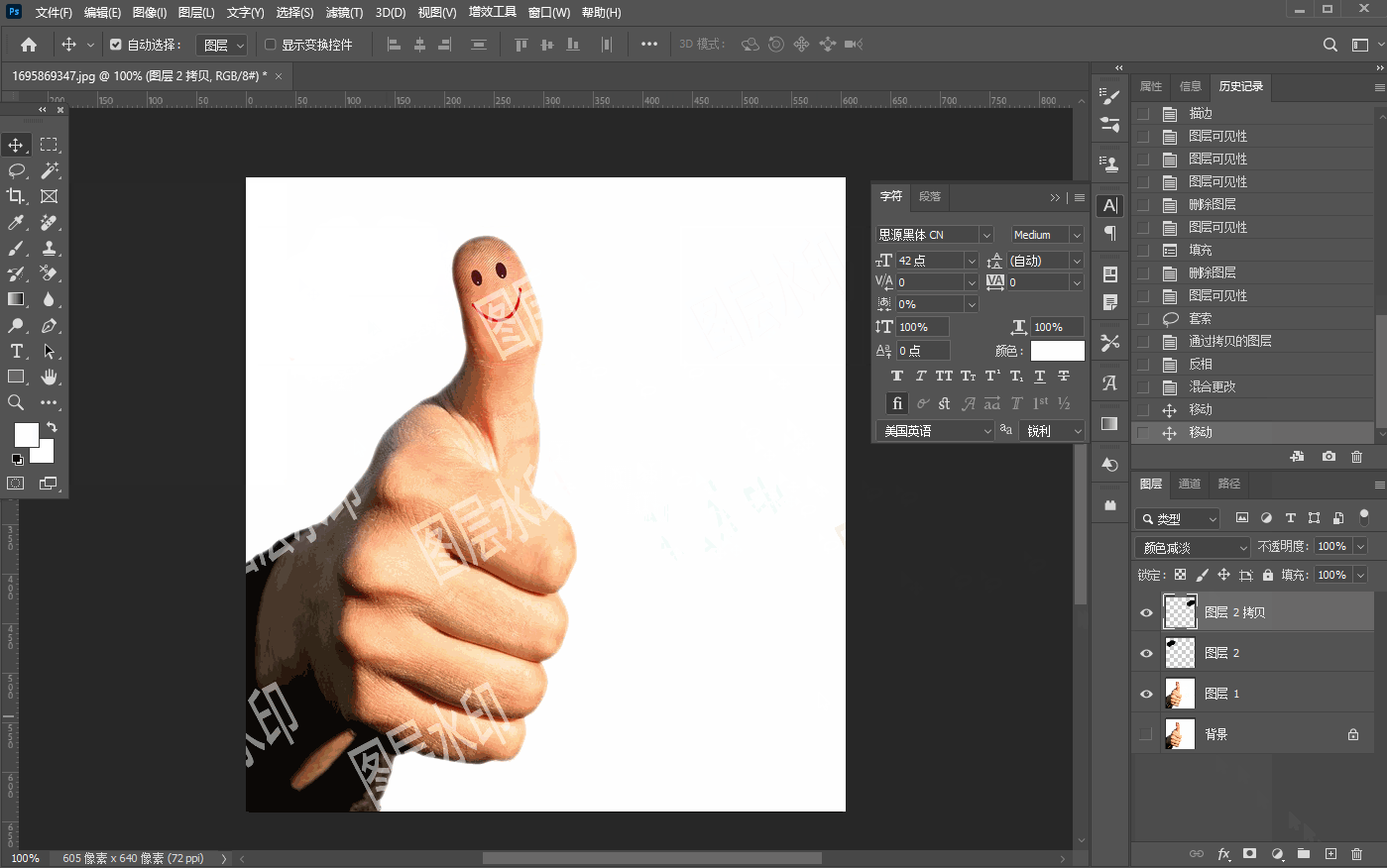
六、【图像去水印】
文章目录 裁剪法移动复制法内容识别去水印色阶法去水印消失点法去水印反相混合法 裁剪法 处于边缘的水印,通过裁剪去除,如下图: 移动复制法 移动复制法适用于水印的背景这部分区域比较相似的情况下使用,如下图先使用矩形选区选中…...
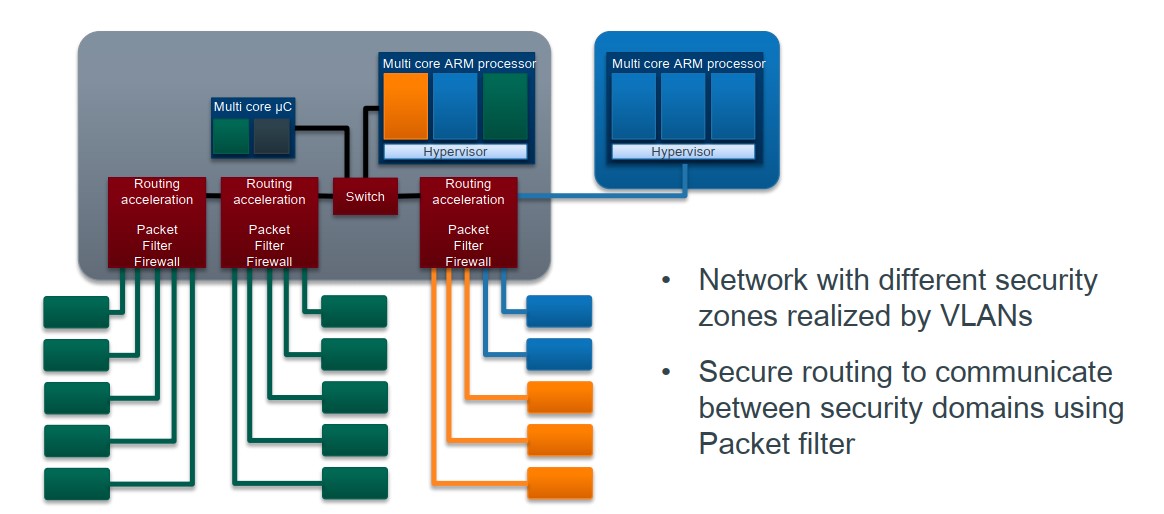
电子电器架构 —— 车载网关初入门(二)
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 PS:小细节,本文字数5000+,详细描述了网关在车载框架中的具体性能设置。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 没有人关注你。也无需有人关注你。你必须承认自己的价值,你不能站在他…...
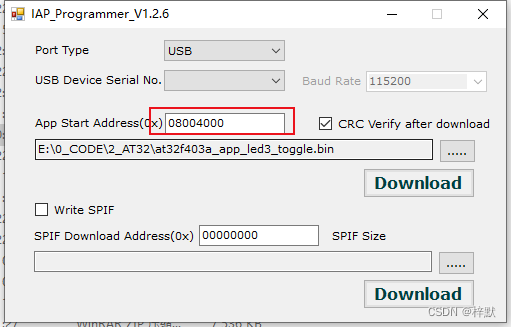
AT32固件库外设使用,ArduinoAPI接口移植,模块化
目录 一、ArduinoAPI移植一、通用定时器使用1.计时1.2.ETR外部时钟计数4.ArduinoAPI - timer 三、ADC1.ADC初始化(非DMA)2.ADC_DMA 规则通道扫描 六、USB HID IAP1.准备好Bootloader和app2.配置好时钟,一定要打开USB3.将生成的时钟配置复制到…...
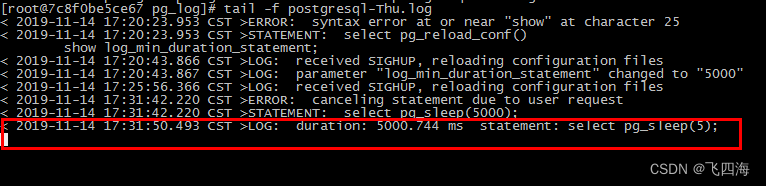
【Postgres】Postgres常用命令
文章目录 1、导出数据库某张表2、导入某张表到数据库3、查看数据库占用磁盘页数情况4、查看数据库大小5、查看数据表大小6、查看索引大小7、对数据库中表索引按照大小排序8、对数据库中表按照大小排序9、回收空间(建议先回收指定表)10、设置主键自增序列…...

pthread 读写锁使用详解
pthread 读写锁使用 读写锁:提供了一种高效的机制来控制对共享资源的访问。允许多个线程同时读取共享资源,但只允许一个线程独占地写入访问。适用于读取远远超过写入的场景下,因为写入操作需要独占地访问资源,可能会影响读取操作…...

MySQL扩展语句
if not exists xiaobu:xiaobu这个表不存在,才会创建 zerofill:自动填充位置 1 0001 primary key:当前表的主键,主键只能有一个,而且唯一,而且不能为空 auto_increment:表示该字段…...
在连接wifi的情况下部分机型下存在的问题)
阿里云号码认证服务(一键登录)在连接wifi的情况下部分机型下存在的问题
手机型号: vivo S16 存在的现象: 安装手机卡(联通卡),且连接wifi的情况下,APP登录唤起阿里云一键登录服务大概有90%左右必超时(按照阿里云一键登录官方文档设置的超时时间为5秒)。 解决方案: 1、APP端增加超时判断&…...

电脑屏幕监控软件,能够帮助企业完成哪些事情?
电脑屏幕监控软件是一种能够监控和管理员工在电脑上的操作行为的软件。分为两种监控方式:实时监控和屏幕记录监控。实时监控是对电脑屏幕进行实时录像,屏幕记录监控则是以屏幕快照的形式保存下来,供使用者随时查看。电脑屏幕监控软件…...

java--方法的其他形式
1.方法定义时:需要按照方法解决的实际业务需求,来设计合理的方法形式解决问题。 1.注意事项 ①如果方法不需要返回数据,返回值类型必须申明成void(无返回值申明),此时方法内部不可以使用return返回数据。 ②方法如果不需要接收数…...
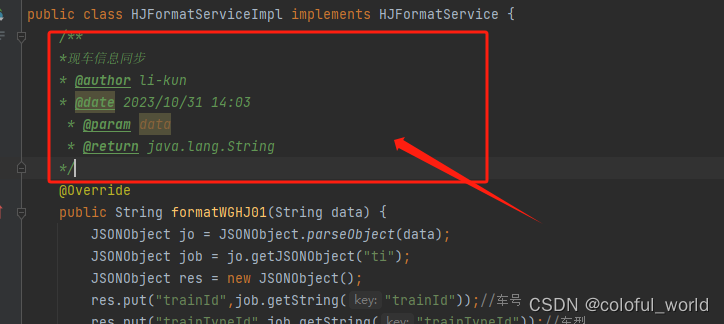
IDEA配置类、方法注释模板
一、打开 IDEA 的 Settings,点击 Editor–>File and Code Templates,点击右边 File 选项卡下面的 Class,在其中添加图中红框内的内容: /** * author li-kun * date ${YEAR}年${MONTH}月${DAY}日 ${TIME} */当你创建一个新的类…...

PowerDesigner 16数据库(mysql)逆向生成pdm
1、配置数据源 2、测试数据源 but~~~~没成功,shift...

Spring Cloud 之Feign
前言 Feign是一个声明式的Web服务客户端,使得编写HTTP客户端变得更简单。在Java程序中,只需要在方法前加上FeignClient注解,Feign就会自动创建一个HTTP客户端,向指定的URL发送请求。 核心概念 1、注解:在服务接口方…...

通用开源自动化测试框架 - Robot Framework
一、什么是 Robot Framework? 1. Robot Framework 的历史由来 Robot Framework是一种通用的自动化测试框架,最早由Pekka Klrck在2005年开发,并由Nokia Networks作为内部工具使用。后来,该项目以开源形式发布,并得到了…...
css position属性与js滚动
“视口”就是浏览器窗口中实际显示文档内容的区域,不包含浏览器的“外框”,如菜单、工具条和标签。文档则是指整个网页。 1 css 的position static 正常定位,是元素position属性的默认值,元素遵循常规流。 relative 相对定位&…...

python内置模块hashlib对于字符串的加密解密加盐
hash是一类算法而hashlib模块是Python的一个内置模块,主要功能是使用对应的hash算法,加密二进制内容解密二进制内容 常见的hash算法有md5、sha1,sha256, sha512等 特点 1.内容敏感,那怕一个很小的字符发生改变都很明显 2.不可逆,不能逆向求值…...

获取客户端请求IP及IP所属城市
添加pom依赖 <dependency> <groupId>org.lionsoul</groupId> <artifactId>ip2region</artifactId> <version>2.6.5</version> </dependency> public class IpUtil { private…...
)
【洛谷 P1106】删数问题 题解(贪心+字符串)
删数问题 题目描述 键盘输入一个高精度的正整数 N N N(不超过 250 250 250 位),去掉其中任意 k k k 个数字后剩下的数字按原左右次序将组成一个新的非负整数。编程对给定的 N N N 和 k k k,寻找一种方案使得剩下的数字组成…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
