考虑时空相关性的风电功率预测误差MATLAB代码
微❤关注“电气仔推送”获得资料(专享优惠)
风电功率预测置信区间误差分析拟合
1.风电功率预测误差--时空相关性
展示第一一个时间段的风电功率预测与实际风电功率值的比较。填充区域表示预测的不确定性,显示了95%置信区间内预测可能的范围。蓝色虚线表示置信区间的上限和下限。这种可视化有助于评估风电功率预测的准确性,并理.解与之相关的不确定性范围。在显示风电功率预测与实际风电功率值的同时,展示预测的不确定性,通过置信区间来描述预测的可信范围。
效果:

风电功率预测的95%置信区间的填充区域,绘制第一个时间段的风电功率预测折线图和实际风电功率值折线图,用虚线绘制表示置信区间上限和下限的两条线。
2.用于对风电场的预测误差进行分析,拟合误差分布,并可视化展示误差随时间和功率的变化情况,以及采样功率的分布。这有助于了解预测误差的特性,评估预测模型的准确性,并为风电场的运营和管理提供参考。
拟合分布
绘制三维概率密度图
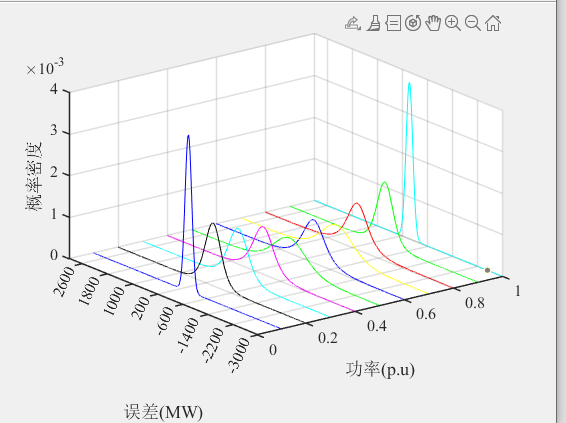
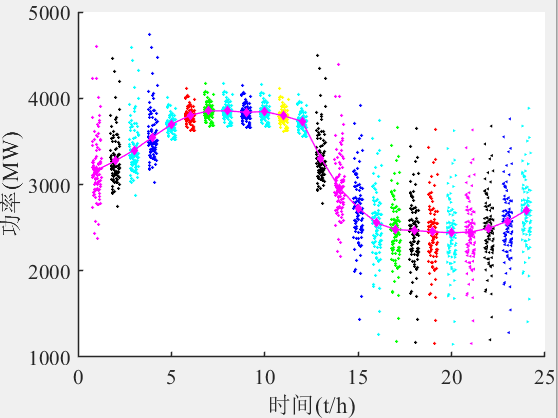
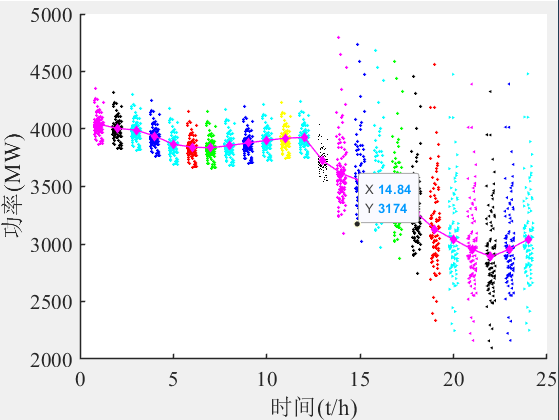
绘制采样功率及功率变化过程:对A风电场的采样功率及一天内的功率变化过程进行了绘制。代码根据每个小时的实际功率值和对应的误差分布,进行100次的随机采样,得到了100 个采样功率值,并对其进行可视化展示。
相关文章:

考虑时空相关性的风电功率预测误差MATLAB代码
微❤关注“电气仔推送”获得资料(专享优惠) 风电功率预测置信区间误差分析拟合 1.风电功率预测误差--时空相关性 展示第一一个时间段的风电功率预测与实际风电功率值的比较。填充区域表示预测的不确定性,显示了95%置信区间内预测可能的范围…...
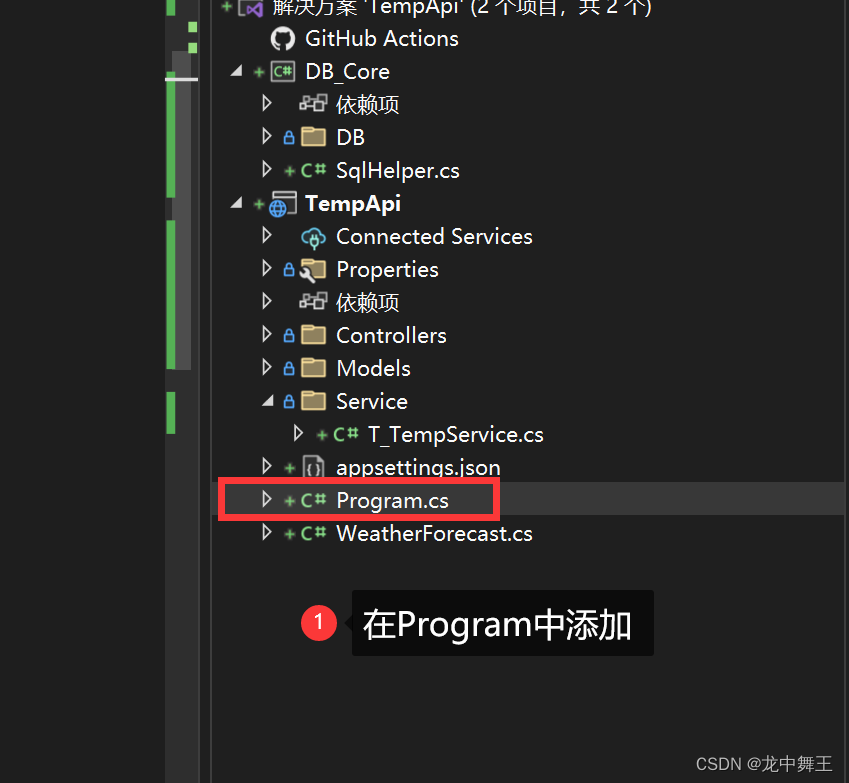
ASP.NET WebApi 极简依赖注入
文章目录 环境服务类启动项注入使用依赖注入的优点 环境 .NET Core 7.0ASP.NET CoreVisual Studio 2022 服务类 public class T_TempService {public T_TempService(){}public void Test(){}}启动项注入 #region 依赖注入 builder.Services.AddTransient<T_TempService&g…...

解决proteus仿真stm32,IIC通讯,IIC DEBUG无法显示从机应答信号的问题(问题情况为在8位数据后应答位显示?)
1、错误现象 错误现象如下,在IIC数据传输8位数据后,IIC DEBUG的应答位无法显示应答位 2、错误原因 我们打开信号传输的示波器,直接去查看IIC从机校验位的数据波形,可以看到从机示波器显示的的波形为半高ACK,那错误原…...

PHP判断闰年
闰年的规则 1.能被4整除且不能被100整除 (普通闰年) 2.能被400整除,公历年份是整百数的,必须是400的倍数才是闰年(世纪闰年) 代码 function isLeapYear($year) {if($year%40 && $year%100!0){r…...

证照之星XE专业版下载专业证件照制作工具
值得肯定的是智能背景替换功能,轻松解决背景处理这一世界难题。不得不提及的是新增打印字体设置,包含字体选择、字号大小、字体颜色等。不同领域的应用证明了万能制作,系统支持自定义证照规格,并预设了17种常用的证件照规格。人所…...

VR全景图片如何制作?揭秘VR全景图片制作全流程
引言: VR全景图片是一种以全景视角为基础的图片制作技术,能够呈现出更为真实、立体的视觉体验。通过VR全景图片,观众可以360环顾四周,仿佛身临其境,提供了一种全新的感官体验,那么如何制作出令人满意的全景…...

vue element el-table-column 循环示例代码
如果你想循环生成多个el-table-column,可以使用v-for指令。以下是一个示例: <template><el-table :data"tableData"><el-table-column v-for"column in columns" :key"column.prop" :label"column.l…...
数据统计分析与绘图实践技术应用)
R语言生物群落(生态)数据统计分析与绘图实践技术应用
R 语言作的开源、自由、免费等特点使其广泛应用于生物群落数据统计分析。生物群落数据多样而复杂,涉及众多统计分析方法。以生物群落数据分析中的最常用的统计方法回归和混合效应模型、多元统计分析技术及结构方程等数量分析方法为主线,通过多个来自经典…...

有了 GPT,还需要付费咨询吗?
之前写过一篇文章《在创业公司,我靠它续命 …》,提到现在写代码基本靠 GPT。现在这种状况不仅没有改变,反而依赖更深。公司立项开发产品的 Linux 版本,全靠我一个人。我之前虽然一直使用 Linux 开发环境,对 Linux 系统…...

如何搭建一台服务器?
一.准备工作 1. 确定服务器类型:根据需求选择适合的服务器类型,如网站服务器、数据库服务器、文件服务器等。 2. 选择操作系统:根据服务器类型选择合适的操作系统,如Linux(如Ubuntu、CentOS)、Windows Se…...
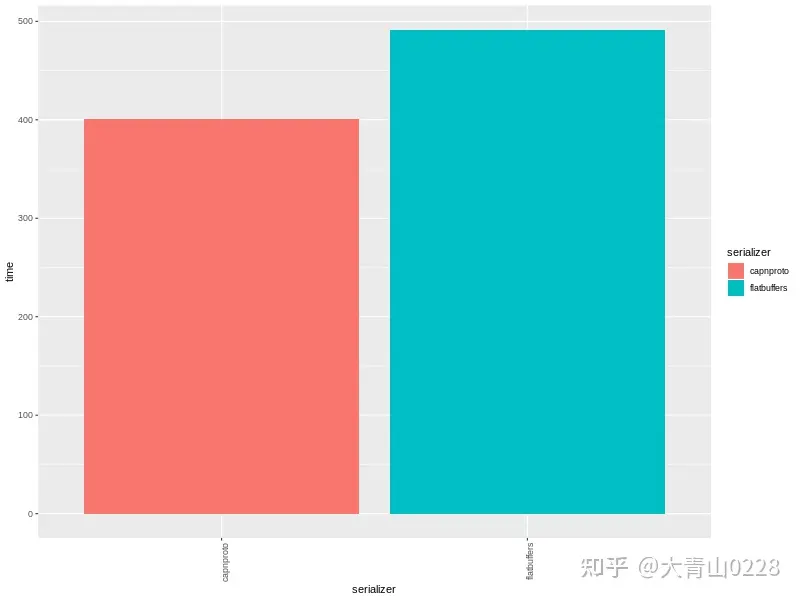
[转载]C++序列化框架介绍和对比
Google Protocol Buffers Protocol buffers 是一种语言中立,平台无关,可扩展的序列化数据的格式,可用于通信协议,数据存储等。 Protocol buffers 在序列化数据方面,它是灵活的,高效的。相比于 XML 来说&…...

分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)
分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制) 目录 分类预测 | Matlab实现KOA-CNN-BiLSTM-selfAttention多特征分类预测(自注意力机制)分类效果基本描述程序设计参考资料 分类效果 基本描述 1…...

浮点数和定点数(上):怎么用有限的Bit表示尽可能多的信息?
目录 背景 浮点数的不精确性 定点数的表示 浮点数的表示 小结 背景 在我们日常的程序开发中,不只会用到整数。更多情况下,我们用到的都是实数。比如,我们开发一个电商 App,商品的价格常常会是 9 块 9;再比如&…...
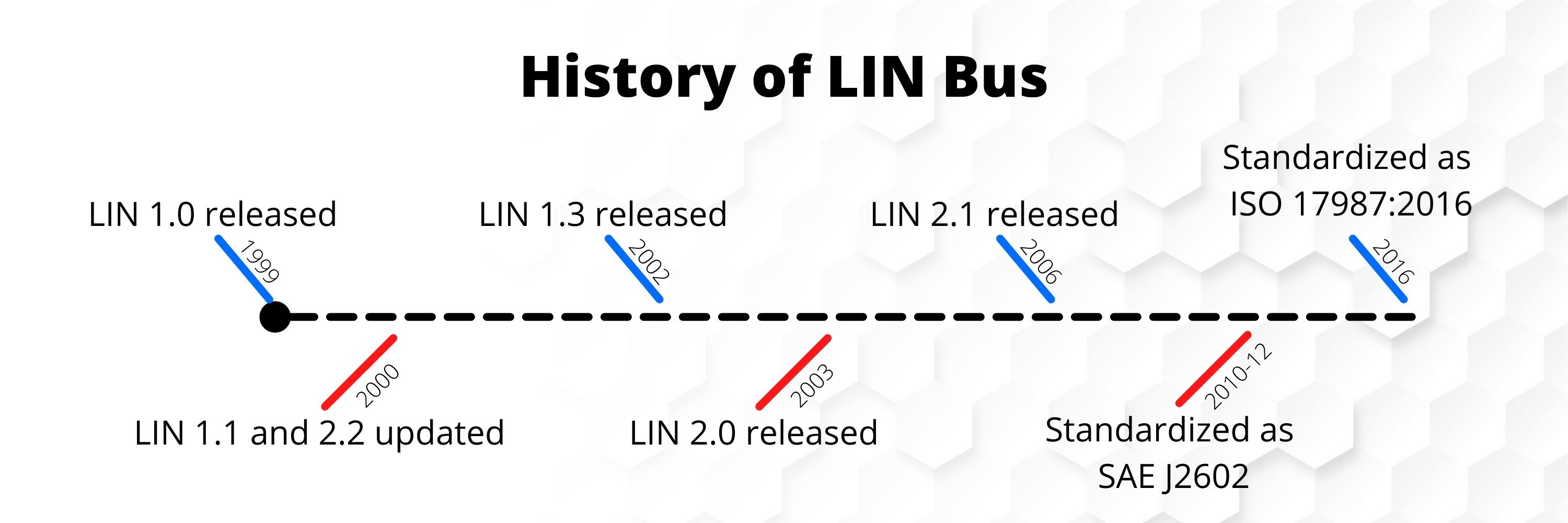
一文详解汽车电子LIN总线
0.摘要 汽车电子LIN总线不同于CAN总线。 LIN总线基本上是CAN总线的廉价补充,相比于CAN总线,它提供较低的可靠性和性能。同时LIN总线也是一个应用非常广泛的网络协议,并且越来越受欢迎。 再一次,我们准备了一个关于LIN总线的简要…...
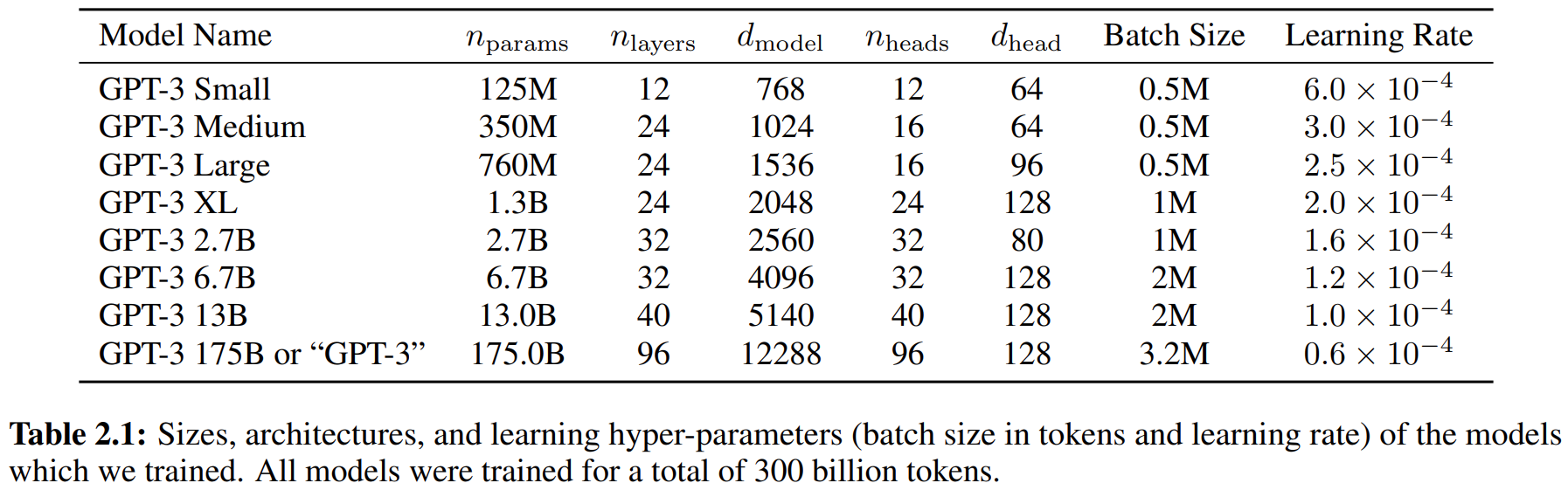
论文阅读——GPT3
来自论文:Language Models are Few-Shot Learners Arxiv:https://arxiv.org/abs/2005.14165v2 记录下一些概念等。,没有太多细节。 预训练LM尽管任务无关,但是要达到好的效果仍然需要在特定数据集或任务上微调。因此需要消除这个…...
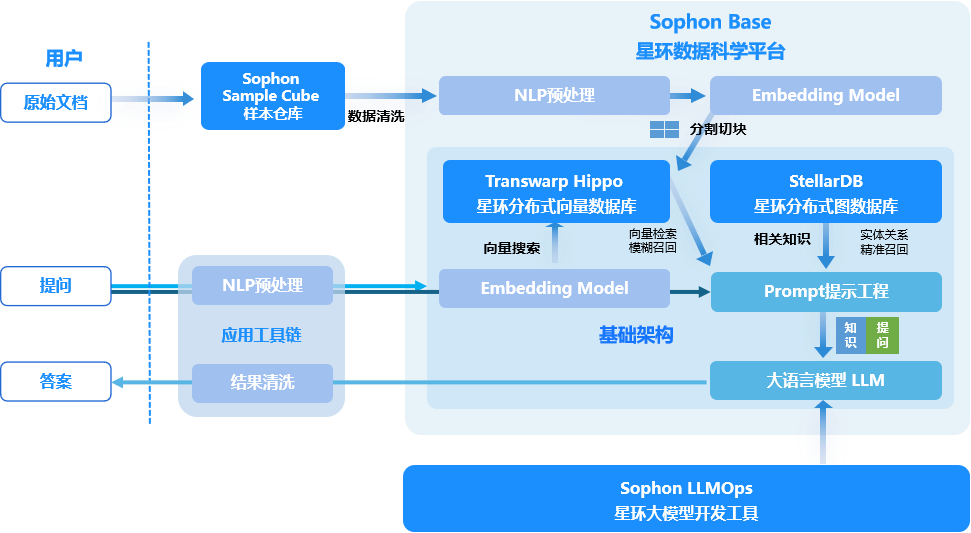
星环科技分布式向量数据库Transwarp Hippo正式发布,拓展大语言模型时间和空间维度
随着企业、机构中非结构化数据应用的日益增多以及AI的爆发式增长所带来的大量生成式数据,所涉及的数据呈现了体量大、格式和存储方式多样、处理速度要求高、潜在价值大等特点。但传统数据平台对这些数据的处理能力较为有限,如使用文件系统、多类不同数据…...
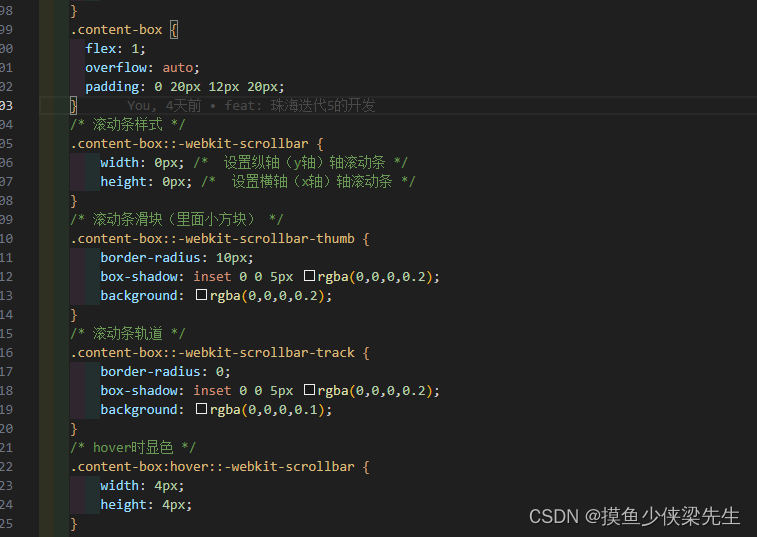
滚动条默认是隐藏的只有鼠标移上去才会显示
效果 在设置滚动条的类名中写 /* 滚动条样式 */.content-box::-webkit-scrollbar {width: 0px; /* 设置纵轴(y轴)轴滚动条 */height: 0px; /* 设置横轴(x轴)轴滚动条 */}/* 滚动条滑块(里面小方块) */.…...
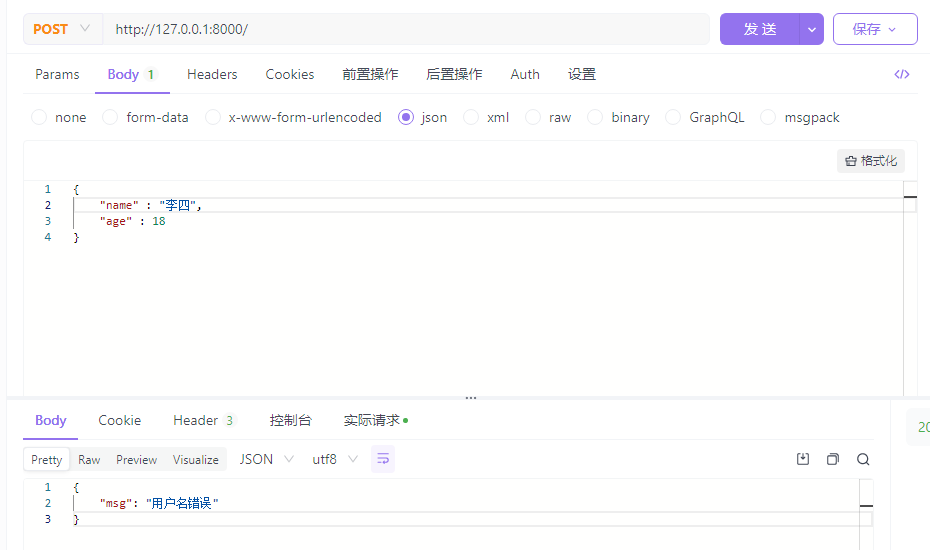
Go学习第十五章——Gin参数绑定bind与验证器
Go web框架——Gin(参数绑定bind与验证器) 1 bind参数绑定1.1 JSON参数1.2 Query参数1.3 Uri绑定动态参数1.4 ShouldBind自动绑定 2 验证器2.1 常用验证器2.2 gin内置验证器2.3 自定义验证的错误信息2.4 自定义验证器 1 bind参数绑定 在Gin框架中&#…...

EtherCAT的4种寻址方式解析
我们知道,一个EtherCAT数据帧(frame)里面包含很多个报文(datagram),不管是什么样式的报文,它们的目的只有一个,就是读写从站寄存器或内存。所以寻址就是以什么方式访问哪个从站的哪个…...
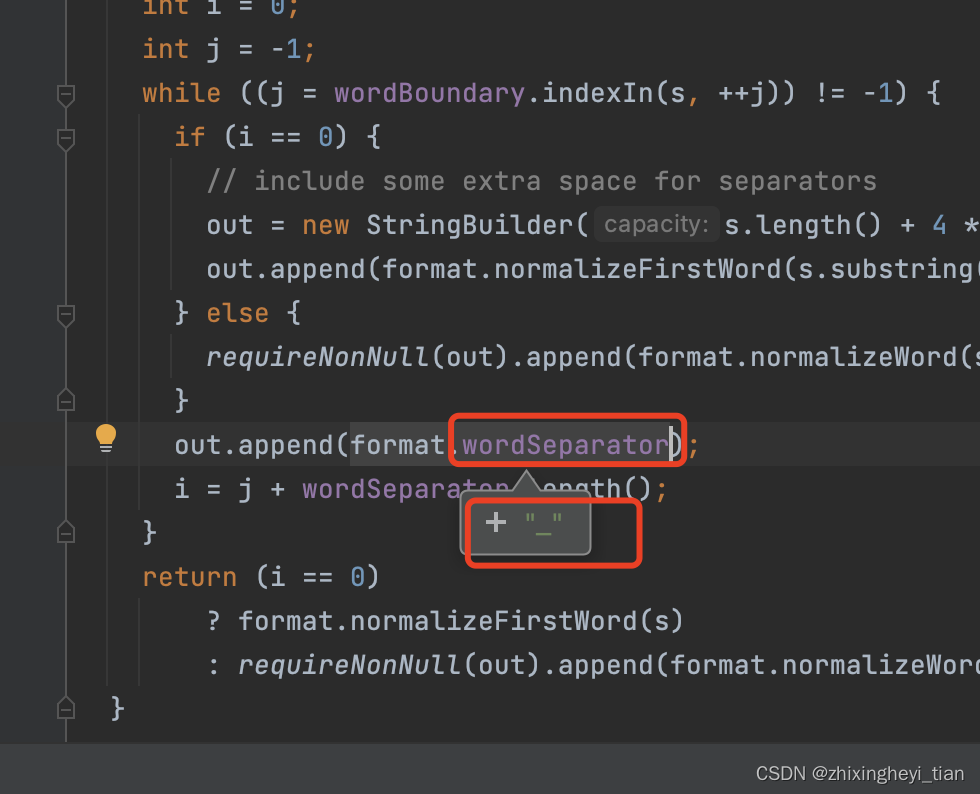
Trino 源码剖析
Functions function 反射和注册 io.trino.operator.scalar.annotations.ScalarFromAnnotationsParser 这里是提取注解元素的方法 String baseName scalarFunction.value().isEmpty() ? camelToSnake(annotatedName(annotated)) : scalarFunction.value(); 这里如果 scala…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
