数据结构(六)二叉树
一、树形结构
概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
1、有一个特殊的结点,称为根结点,根结点没有前驱结点
2、除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合 Ti (1 <= i<= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
3、树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
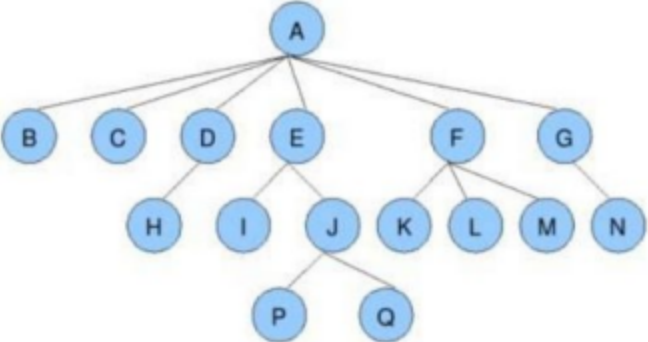
结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等节点为叶结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
根结点:一棵树中,没有双亲结点的结点;如上图:A
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
树的以下概念只需了解,在看书时只要知道是什么意思即可:
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由m(m>=0)棵互不相交的树组成的集合称为森林
二、二叉树
概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
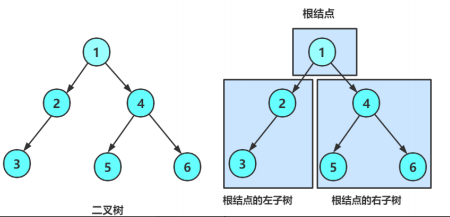
从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:

两种特殊的二叉树
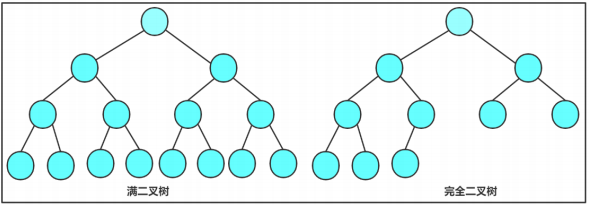
1. 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵
二叉树的层数为K,且结点总数是
,则它就是满二叉树。
2. 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n
个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完
全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
二叉树的性质
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1)(i>0)个结点
2. 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2^k-1(k>=0)
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
4. 具有n个结点的完全二叉树的深度k为 log2(n+1)上取整
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
-若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
-若2i+1<n,左孩子序号:2i+1,否则无左孩子
-若2i+2<n,右孩子序号:2i+2,否则无右孩子
二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}孩子双亲表示法后序在平衡树位置介绍,本文采用孩子表示法来构建二叉树
二叉树的基本操作
class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}
}
public class TestBinaryTree {public TreeNode creteTree(){TreeNode A=new TreeNode('A');TreeNode B=new TreeNode('B');TreeNode C=new TreeNode('C');TreeNode D=new TreeNode('D');TreeNode E=new TreeNode('E');TreeNode F=new TreeNode('F');TreeNode G=new TreeNode('G');TreeNode H=new TreeNode('H');A.left=B;A.right=C;B.left=D;B.right=E;E.right=H;C.left=F;C.right=G;return A;//根节点}// 前序遍历void preOrder(TreeNode root){if (root==null){return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}// 中序遍历void inOrder(TreeNode root){if (root==null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}// 后序遍历void postOrder(TreeNode root){if (root==null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}public static int count=0;// 获取树中节点的个数int size1(TreeNode root) {if (root==null){return 0;}count++;size1(root.left);size1(root.right);return count;}public int size(TreeNode root){if (root==null){return 0;}int tmp=size(root.left)+size(root.right)+1;return tmp;}public static int leafCount=0;// 获取叶子节点的个数void getLeafNodeCount1(TreeNode root) {if (root==null){return;}if (root.left==null&&root.right==null){leafCount++;}getLeafNodeCount1(root.left);getLeafNodeCount1(root.right);}// 子问题思路-求叶子结点个数public int getLeafNodeCount(TreeNode root){if (root==null){return 0;}if (root.left==null&&root.right==null){return 1;}int tmp=getLeafNodeCount(root.left)+getLeafNodeCount(root.right);return tmp;}// 获取第K层节点的个数int getKLevelNodeCount(TreeNode root,int k){if (root==null){return 0;}if (k==1){return 1;}int tmp=getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);return tmp;}// 获取二叉树的高度int getHeight(TreeNode root) {if (root==null){return 0;}int leftH=getHeight(root.left);int rightH=getHeight(root.right);return leftH > rightH ? leftH+1 : rightH+1;}// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val) {if (root==null){return null;}if (root.val==val){return root;}TreeNode ret=find(root.left,val);if (ret!=null){return ret;}ret=find(root.right,val);if (ret!=null){return ret;}return null;}
}相关文章:

数据结构(六)二叉树
一、树形结构概念树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:1、有一个…...
Docker buildx 的跨平台编译
docker buildx 默认的 docker build 命令无法完成跨平台构建任务,我们需要为 docker 命令行安装 buildx 插件扩展其功能。buildx 能够使用由 Moby BuildKit 提供的构建镜像额外特性,它能够创建多个 builder 实例,在多个节点并行地执行构建任…...

【java基础】方法重载和方法重写
文章目录方法重载方法重写方法重载 方法重载就是可以在一个类里面定义多个相同名称的方法,只需要参数列表的个数或者类型不同就行。 public class Overload {public int add(int a, int b) {return a b;}public double add(double a, double b) {return a b;}}对…...
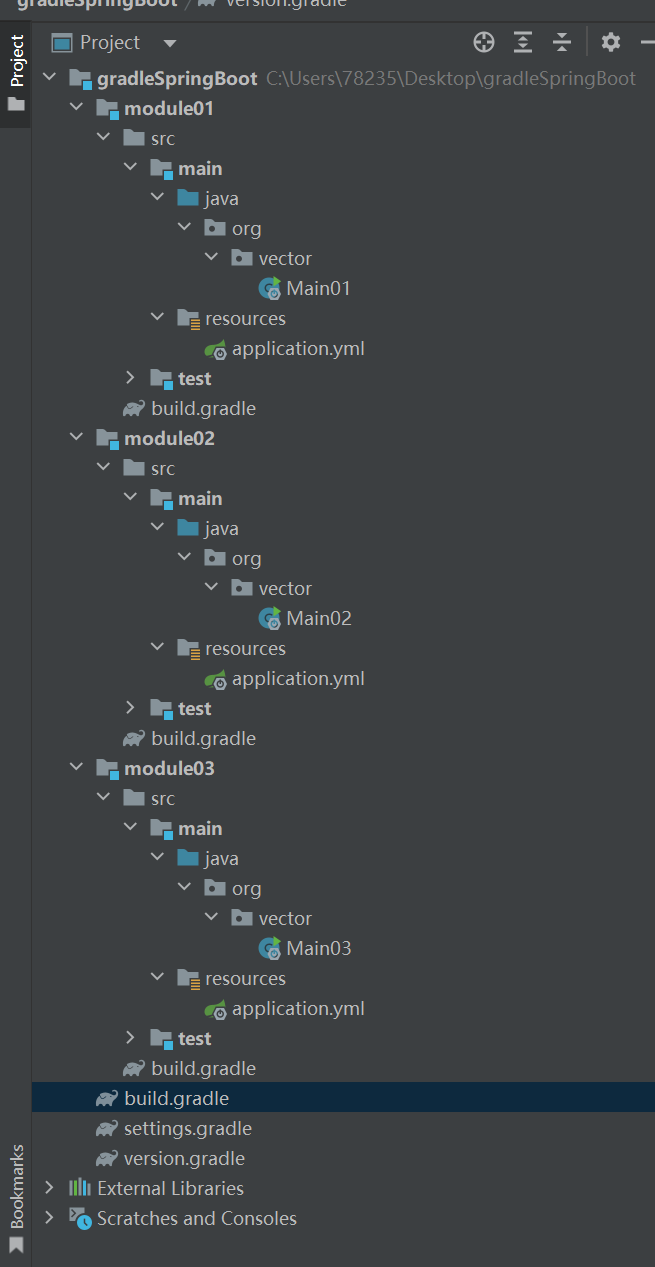
Gradle7.4安装与基本使用
文章目录一.前言二.下载Gradle三.Gradle镜像源-全局级配置四.配置Gradle wrapper-项目级配置五.Gradle对测试的支持五.生命周期5.1 settings文件六.Gradle任务入门6.1 任务行为6.2 任务依赖方式七. Dependencies依赖引入7.1 依赖冲突及解决方案八.Gradle整合多模块SpringBoot九…...

[系统安全] 虚拟化安全之虚拟化概述
本文为笔者从零基础学习系统安全相关内容的笔记,如果您对系统安全、逆向分析等内容感兴趣或者想要了解一些内容,欢迎关注。本系列文章将会随着笔者在未来三年的读研过程中持续更新,由于笔者现阶段还处于初学阶段,不可避免参照复现各类书籍内容,如书籍作者认为侵权请告知,…...

如何从零开始系统的学习项目管理?
经常会有人问,项目管理到底应该学习一些什么?学习考证之后能得到什么价值? 以下我就总结一下内容 一,学习项目管理有用吗? 有效的项目管理带来的益处大致包括以下几个方面:更有效达成业务目标、满足相关…...

面试题-----
面试题---- 一.HTML 1.常用哪些浏览器进行测试,对应有哪些内核? ①IE------------------->Trident ②Chrome---------->以前是Webkit现在是Blink ③Firefox------------>Gecko ④Safari-------------->Webkit ⑤Opera--------------&…...
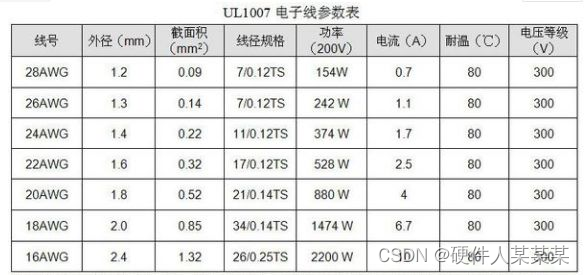
线材-电子线载流能力
今天来讲的是关于电子线的一个小知识,可能只做板子的工程师遇到此方面的问题会比较少,做整机的工程师则必然会遇到此方面问题,那就是线材问题。 下面主要说下电子线的过电流能力。(文末有工具下载)电子线(h…...
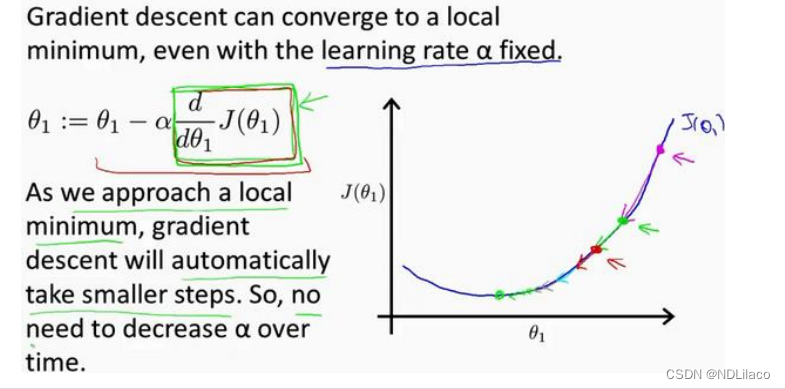
单变量回归问题
单变量回归问题 对于某房价问题,x为房屋大小,h即为预估房价,模型公式为: hθ(x)θ0θ1xh_{\theta}(x)\theta_{0}\theta_{1}x hθ(x)θ0θ1x 要利用训练集拟合该公式(主要是计算θ0、θ1\theta_{0}、\theta_{1}θ…...
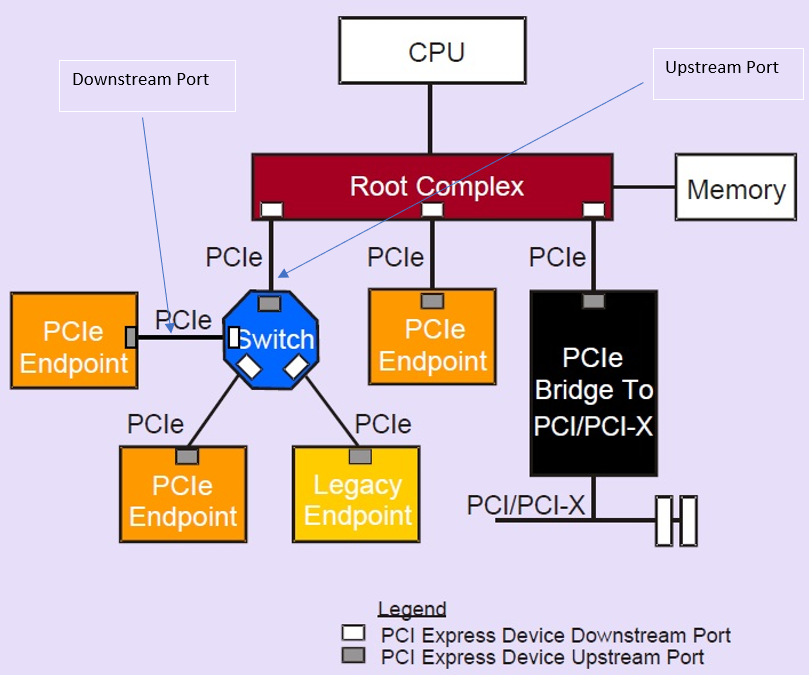
ubuntu/linux系统知识(36)linux网卡命名规则
文章目录背景命名规范系统默认命名规则优势背景 很久以前Linux 操作系统的网卡设备的传统命名方式是 eth0、eth1、eth2等,属于biosdevname 命名规范。 服务器通常有多块网卡,有板载集成的,同时也有插在PCIe插槽的。Linux系统的命名原来是et…...
java的一些冷知识
接口并没有继承Object类首先接口是一种特殊的类,理由就是将其编译后是一个class文件大家都知道java类都继承自Object,但是接口其实是并没有继承Object类的 可以自己写代码测试: 获取接口类的class对象后遍历它的methods,可以发现是不存在Obje…...

java代理模式
代理模式 为什么要学习代理模式?因为这是SpringAOP的底层! 【SpringAOP和SpingMVC}】 代理模式的分类: 静态代理 动态代理 代理就像这里的中介,帮助你去做向房东租房,你不能直接解出房东,而房东和中介…...
JUC包:CountDownLatch源码+实例讲解
1 缘起 有一次听到同事谈及AQS时,我有很多点懵, 只知道入队和出队,CLH(Craig,Landin and Hagersten)锁,并不了解AQS的应用, 同时结合之前遇到的多线程等待应用场景,发现…...

Log4j2基本使用
文章目录1. Log4j2入门2. Log4j2配置3. Log4j2异步日志4. Log4j2的性能Apache Log4j 2是对Log4j的升级版,参考了logback的一些优秀的设计,并且修复了一些问题,因此带 来了一些重大的提升,主要有: 异常处理,…...

A2L在CAN FD总线的使用
文章目录 前言CAN时间参数BTL CyclesTime Quantum时间份额SWJ同步跳转宽度波特率计算采样点计算CAN FD的第二采样点SSP推荐配置A2L配置总结前言 A2L作为XCP标定协议的载体,包括了总线信息的定义。本文介绍如何将基于CAN总线的A2L扩展为支持CAN-FD的A2L CAN时间参数 在介绍配…...

Android JetPack之启动优化StartUp初始化组件的详解和使用
一、背景 先看一下Android系统架构图 在Android设备中,设备先通电(PowerManager),然后加载内核层,内核走完,开始检查硬件,以及为硬件提供的公开接口,然后进入到库的加载。库挂载后开…...
[11]云计算|简答题|案例分析|云交付|云部署|负载均衡器|时间戳
升级学校云系统我们学校要根据目前学生互联网在线学习、教师教学资源电子化、教学评价过程化精细化的需求,计划升级为云教学系统。请同学们根据学校发展实际考虑云交付模型包含哪些?云部署采用什么模型最合适?请具体说明。9月3日买电脑还是租…...

C++11/C++14:lambda表达式
概念 lambda表达式:是一种表达式,是源代码的组成部分闭包:是lambda表达式创建的运行期对象,根据不同的捕获模式,闭包会持有数据的副本或引用闭包类:用于实例化闭包的类,每个lambda表达式都会触…...

算法课堂-分治算法
分治算法 把一任务分成几部分(通常是两部分)来完成(或只完成一部分),从而实现整个任务的完成 或者你可以把递归理解为分治算法的一部分 因为递归就是把问题分解来解决问题 例子 称假币 最笨的方法:两两称…...

操作系统权限提升(十六)之绕过UAC提权-CVE-2019-1388 UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权 操作系统权限提升(十四)之绕过UAC提权-基于白名单AutoElevate绕过UAC提权 操作系统权限提升(十五)之绕过UAC提权-基于白名单DLL劫持绕过UAC提权 注&a…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
