单变量回归问题
单变量回归问题
对于某房价问题,x为房屋大小,h即为预估房价,模型公式为:
hθ(x)=θ0+θ1xh_{\theta}(x)=\theta_{0}+\theta_{1}x hθ(x)=θ0+θ1x
要利用训练集拟合该公式(主要是计算θ0、θ1\theta_{0}、\theta_{1}θ0、θ1),需要代价函数(计算当前模型和测试集数据的误差),
J(θ0,θ1)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta_{0},\theta_{1})=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
当代价函数得到最小值时,此时拟合的公式最好。一般利用梯度下降法来得到代价函数的局部(全局)最优解。批量梯度下降的公式为
θj:=θj−α∂∂θjJ(θ0,θ1)(forj=0andj=1)\theta_{j}:=\theta_{j}-\alpha\frac{\partial }{\partial \theta_{j}}J(\theta_{0},\theta_{1}) (for \quad j=0\quad and \quad j=1) θj:=θj−α∂θj∂J(θ0,θ1)(forj=0andj=1)
∂∂θjJ(θ0,θ1)=∂∂θj(12m∑i=1m(hθ(x(i))−y(i))2)\frac{\partial }{\partial \theta_{j}}J(\theta_{0},\theta_{1})=\frac{\partial }{\partial \theta_{j}}(\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2}) ∂θj∂J(θ0,θ1)=∂θj∂(2m1i=1∑m(hθ(x(i))−y(i))2)
j=0时,∂∂θ0J(θ0,θ1)=1m∑i=1m(hθ(x(i))−y(i))j=0时,\frac{\partial }{\partial \theta_{0}}J(\theta_{0},\theta_{1})=\frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})} j=0时,∂θ0∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))
j=1时,∂∂θ1J(θ0,θ1)=1m∑i=1m(hθ(x(i))−y(i))⋅x(i)j=1时,\frac{\partial }{\partial \theta_{1}}J(\theta_{0},\theta_{1})=\frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})\cdot x^{(i)}} j=1时,∂θ1∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))⋅x(i)
α\alphaα为学习率,决定沿着代价函数下降程度最大的方向向下的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
如果α\alphaα太小了,即我的学习速率太小,需要很多步才能到达最低点,可能会很慢;
如果α\alphaα太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛。
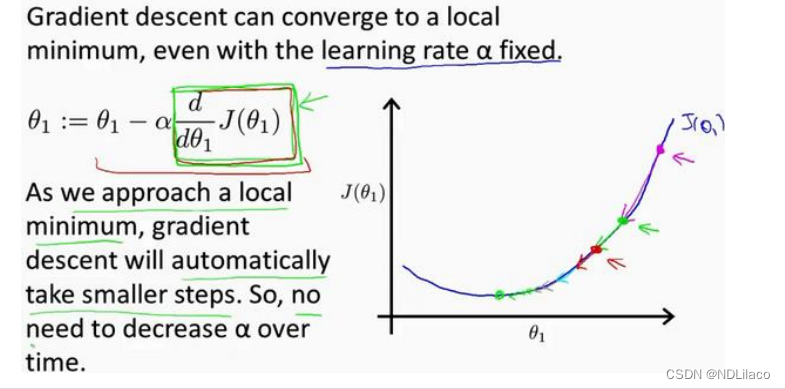
在梯度下降法中,当我们接近局部最低点时,梯度下降法会自动采取更小的幅度,这是因为当我们接近局部最低点时,很显然在局部最低时导数等于零,所以当我们接近局部最低时,导数值会自动变得越来越小,所以梯度下降将自动采取较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小α\alphaα。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qARHfSRE-1677383475783)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230222172604462.png)]](https://img-blog.csdnimg.cn/2fd583aba931446d8b75b4280f9a43c5.png)
相关文章:
单变量回归问题
单变量回归问题 对于某房价问题,x为房屋大小,h即为预估房价,模型公式为: hθ(x)θ0θ1xh_{\theta}(x)\theta_{0}\theta_{1}x hθ(x)θ0θ1x 要利用训练集拟合该公式(主要是计算θ0、θ1\theta_{0}、\theta_{1}θ…...
ubuntu/linux系统知识(36)linux网卡命名规则
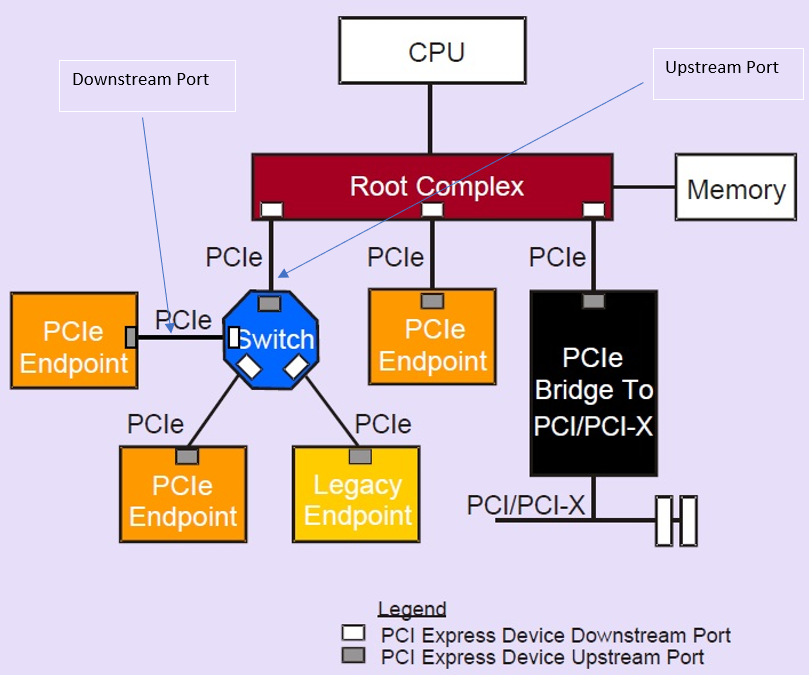
文章目录背景命名规范系统默认命名规则优势背景 很久以前Linux 操作系统的网卡设备的传统命名方式是 eth0、eth1、eth2等,属于biosdevname 命名规范。 服务器通常有多块网卡,有板载集成的,同时也有插在PCIe插槽的。Linux系统的命名原来是et…...
java的一些冷知识
接口并没有继承Object类首先接口是一种特殊的类,理由就是将其编译后是一个class文件大家都知道java类都继承自Object,但是接口其实是并没有继承Object类的 可以自己写代码测试: 获取接口类的class对象后遍历它的methods,可以发现是不存在Obje…...

java代理模式
代理模式 为什么要学习代理模式?因为这是SpringAOP的底层! 【SpringAOP和SpingMVC}】 代理模式的分类: 静态代理 动态代理 代理就像这里的中介,帮助你去做向房东租房,你不能直接解出房东,而房东和中介…...
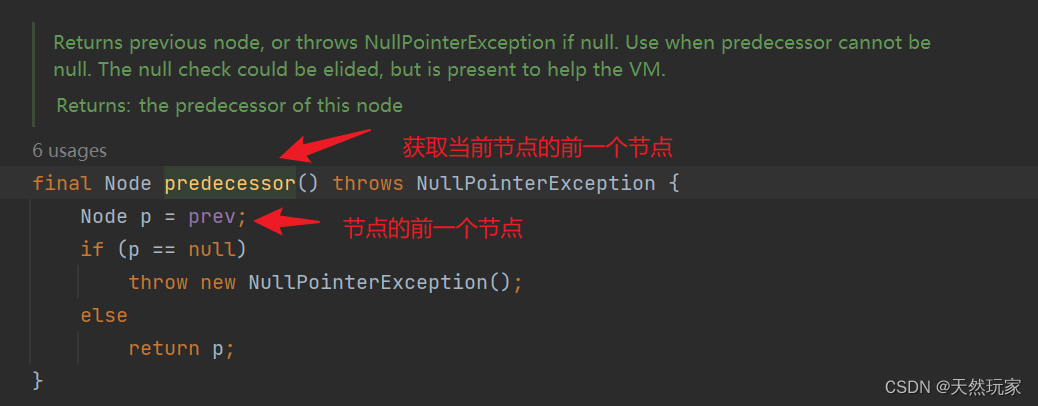
JUC包:CountDownLatch源码+实例讲解
1 缘起 有一次听到同事谈及AQS时,我有很多点懵, 只知道入队和出队,CLH(Craig,Landin and Hagersten)锁,并不了解AQS的应用, 同时结合之前遇到的多线程等待应用场景,发现…...

Log4j2基本使用
文章目录1. Log4j2入门2. Log4j2配置3. Log4j2异步日志4. Log4j2的性能Apache Log4j 2是对Log4j的升级版,参考了logback的一些优秀的设计,并且修复了一些问题,因此带 来了一些重大的提升,主要有: 异常处理,…...

A2L在CAN FD总线的使用
文章目录 前言CAN时间参数BTL CyclesTime Quantum时间份额SWJ同步跳转宽度波特率计算采样点计算CAN FD的第二采样点SSP推荐配置A2L配置总结前言 A2L作为XCP标定协议的载体,包括了总线信息的定义。本文介绍如何将基于CAN总线的A2L扩展为支持CAN-FD的A2L CAN时间参数 在介绍配…...

Android JetPack之启动优化StartUp初始化组件的详解和使用
一、背景 先看一下Android系统架构图 在Android设备中,设备先通电(PowerManager),然后加载内核层,内核走完,开始检查硬件,以及为硬件提供的公开接口,然后进入到库的加载。库挂载后开…...
[11]云计算|简答题|案例分析|云交付|云部署|负载均衡器|时间戳
升级学校云系统我们学校要根据目前学生互联网在线学习、教师教学资源电子化、教学评价过程化精细化的需求,计划升级为云教学系统。请同学们根据学校发展实际考虑云交付模型包含哪些?云部署采用什么模型最合适?请具体说明。9月3日买电脑还是租…...

C++11/C++14:lambda表达式
概念 lambda表达式:是一种表达式,是源代码的组成部分闭包:是lambda表达式创建的运行期对象,根据不同的捕获模式,闭包会持有数据的副本或引用闭包类:用于实例化闭包的类,每个lambda表达式都会触…...

算法课堂-分治算法
分治算法 把一任务分成几部分(通常是两部分)来完成(或只完成一部分),从而实现整个任务的完成 或者你可以把递归理解为分治算法的一部分 因为递归就是把问题分解来解决问题 例子 称假币 最笨的方法:两两称…...

操作系统权限提升(十六)之绕过UAC提权-CVE-2019-1388 UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权 操作系统权限提升(十四)之绕过UAC提权-基于白名单AutoElevate绕过UAC提权 操作系统权限提升(十五)之绕过UAC提权-基于白名单DLL劫持绕过UAC提权 注&a…...
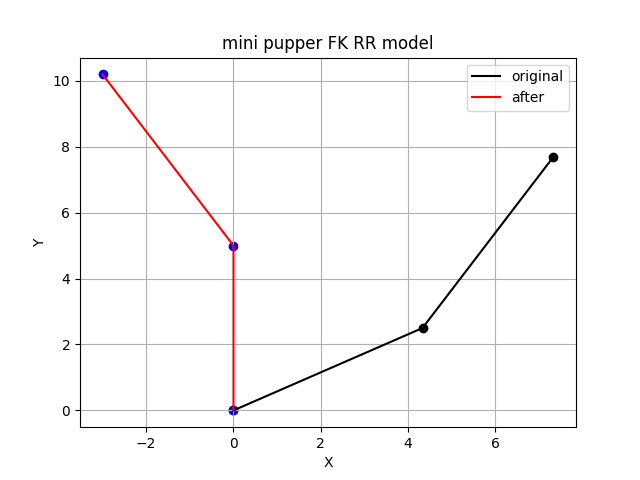
实例9:四足机器人运动学正解平面RR单腿可视化
实例9:四足机器人正向运动学单腿可视化 实验目的 通过动手实践,搭建mini pupper四足机器人的腿部,掌握机器人单腿结构。通过理论学习,熟悉几何法、旋转矩阵法在运动学正解(FK)中的用处。通过编程实践&…...
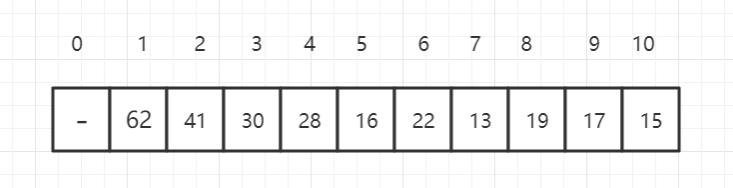
堆的基本存储
一、概念及其介绍堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。堆满足下列性质:堆中某个节点的值总是不大于或不小于其父节点的值。堆总是一棵完全二叉树。二、适用说明堆是利用完全二叉树的结构来维护一组数…...

如何获取物体立体信息通过一个相机
大家都知道的3D 技术是通过双眼视觉差异 得到的 但是3D的深度并没有那么强 为什么眼睛看到的就那么强 这无法让我们相信这个视觉差理论是和人眼睛立体感是一个原理 这个如今3D 电影都在用的技术 是和真正的人眼立体感 不一样的 或者说是有瑕疵的 分析一下现在的立体感技术 是通…...
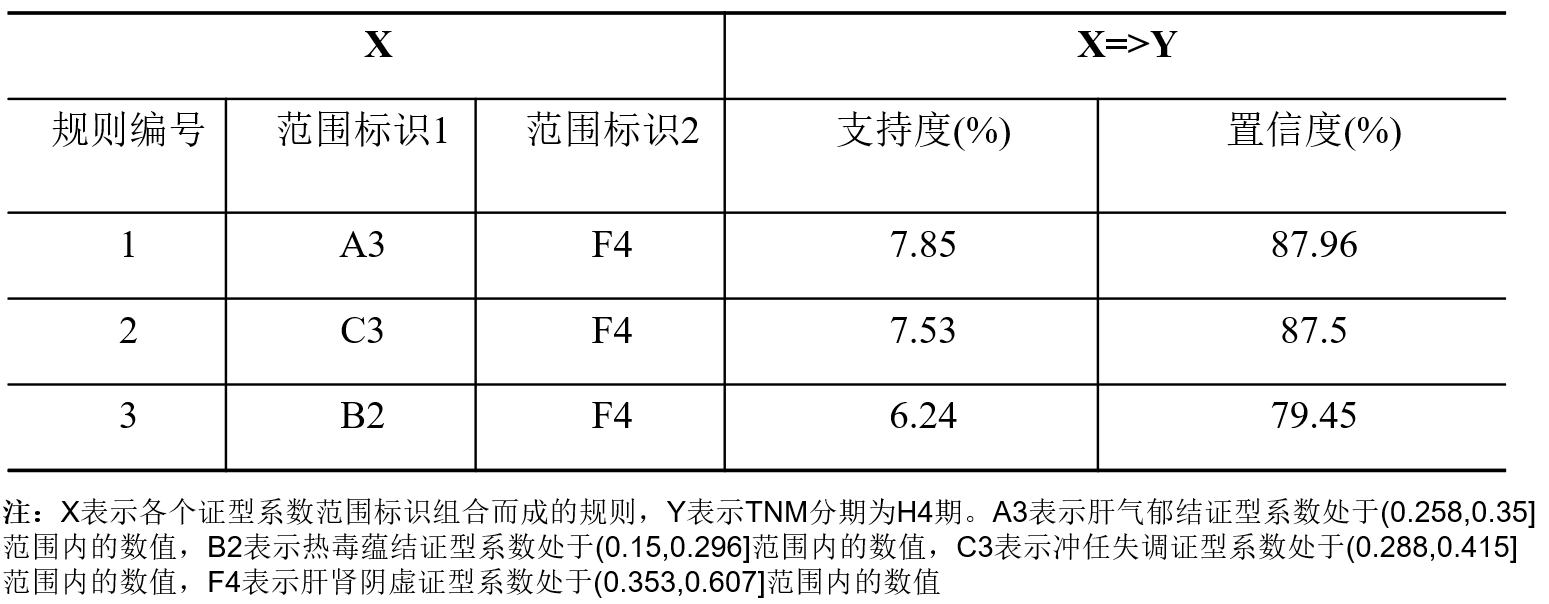
【数据挖掘实战】——中医证型的关联规则挖掘(Apriori算法)
目录 一、背景和挖掘目标 1、问题背景 2、传统方法的缺陷 3、原始数据情况 4、挖掘目标 二、分析方法和过程 1、初步分析 2、总体过程 第1步:数据获取 第2步:数据预处理 第3步:构建模型 三、思考和总结 项目地址:Data…...
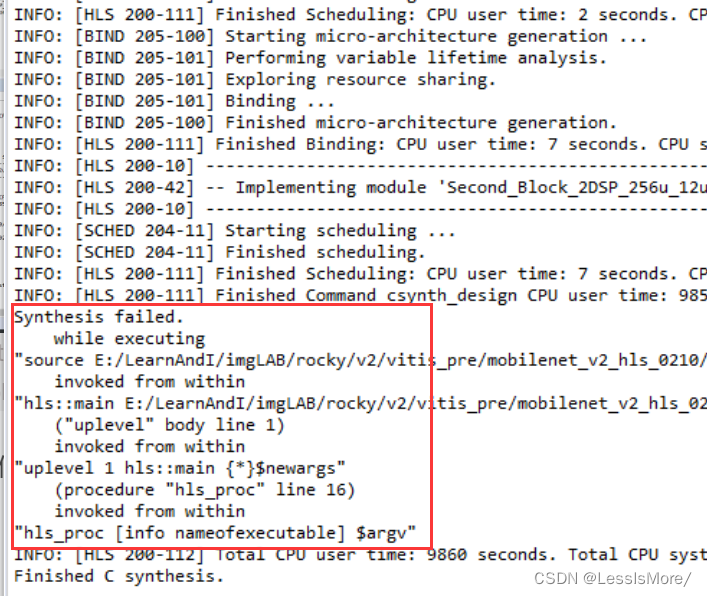
一些硬件学习的注意事项与快捷方法
xilinx系列软件 系统适用版本 要安装在Ubuntu系统的话,要注意提前看好软件适用的版本,不要随便安好了Ubuntu系统又发现对应版本的xilinx软件不支持。 如下图,发行说明中会说明这个版本的软件所适配的系统版本。 下载 vivado vitis这些都可以…...
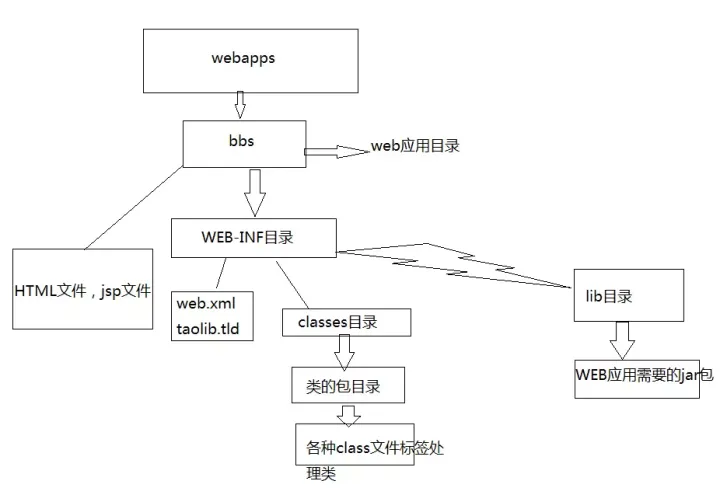
【Tomcat】Tomcat安装及环境配置
文章目录什么是Tomcat为什么我们需要用到Tomcattomcat下载及安装1、进入官网www.apache.org,找到Projects中的project List2、下载之后,解压3、找到tomcat目录下的startup.bat文件,双击之后最后结果出现多少多少秒,表示安装成功4、…...
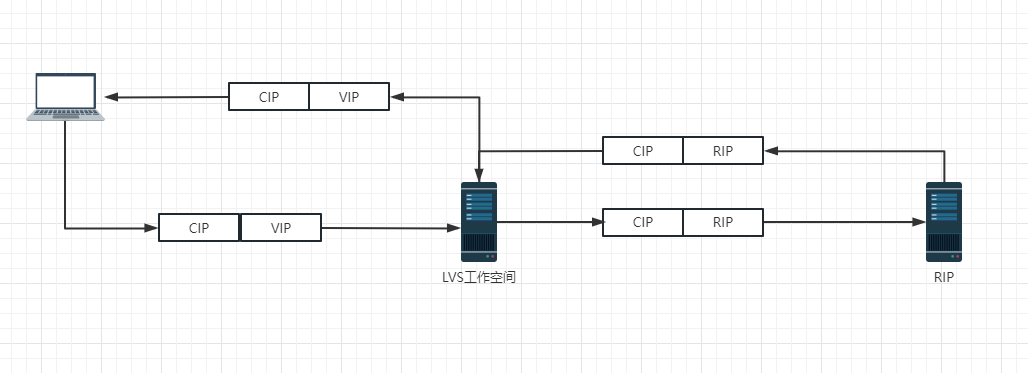
负载均衡:LVS 笔记(二)
文章目录LVS 二层负载均衡机制LVS 三层负载均衡机制LVS 四层负载均衡机制LVS 调度算法轮叫调度(RR)加权轮叫调度(WRR)最小连接调度(LC)加权最小连接调度(WLC)基于局部性的最少链接调…...
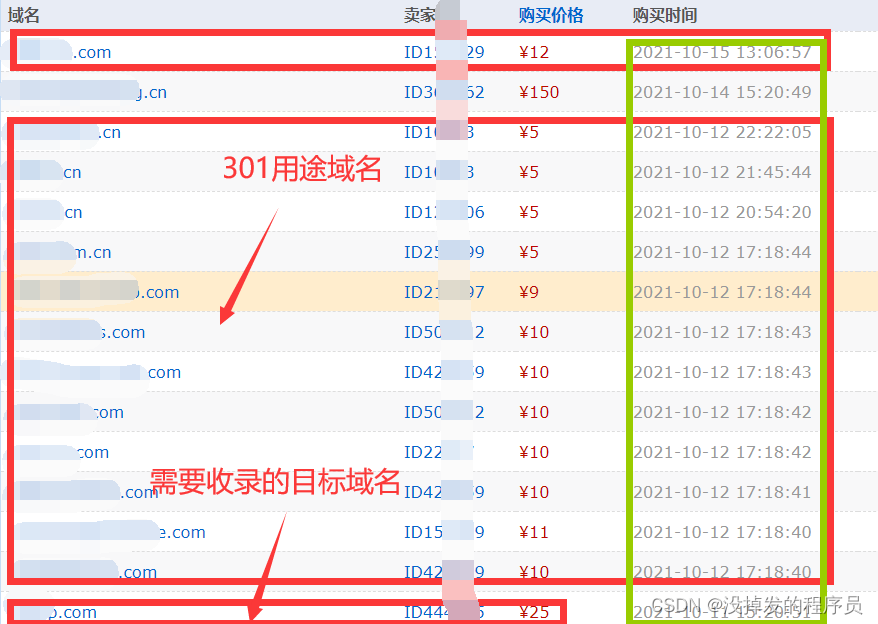
SEO优化:干货技巧分享,包新站1-15天100%收录首页
不管是老域名还是新域名,不管是多久没有收录首页的站,此法周期7-30天,包首页收录!本人不喜欢空吹牛逼不实践的理论,公布具体操作:假如你想收录的域名是a.com,那么准备如下材料1.购买5-10个最便宜…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
