当前位置： 首页 > news >正文

网站模板编辑/微信平台推广方法

news 文章来源：https://blog.csdn.net/weixin_42216109/article/details/134101767 2025/2/27 22:55:17
网站模板编辑,微信平台推广方法,一二三四在线观看免费中文吗,优惠网站代理怎么做问题1. 源码管理处填入Repository URL，报错：无法连接仓库：Error performing git command: ls-remote -h https://github.com/txy2023/GolangLearning.git HEAD 原因： jenkins全局工具配置里默认没有添加git的路径，如果…

问题1. 源码管理处填入Repository URL，报错：无法连接仓库：Error performing git command: ls-remote -h https://github.com/txy2023/GolangLearning.git HEAD

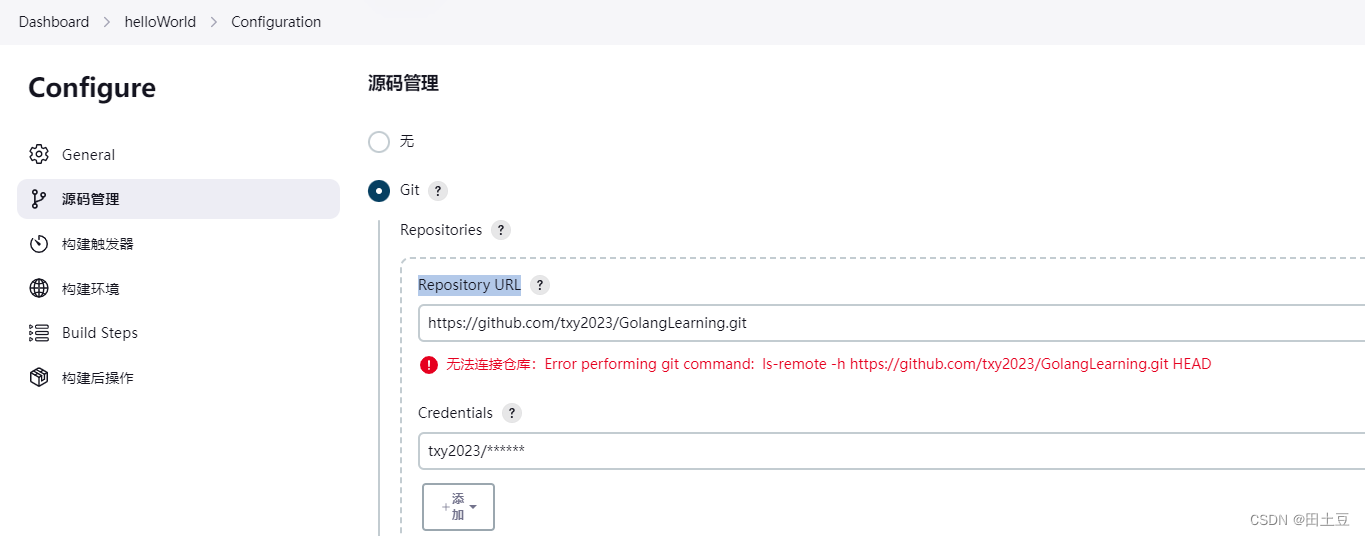
在这里插入图片描述
原因：
jenkins全局工具配置里默认没有添加git的路径，如果你是centos系统，可以which git获取git路径。然后从Dashboard依次点击系统管理-全局工具配置，在Path to Git executable填入git路径
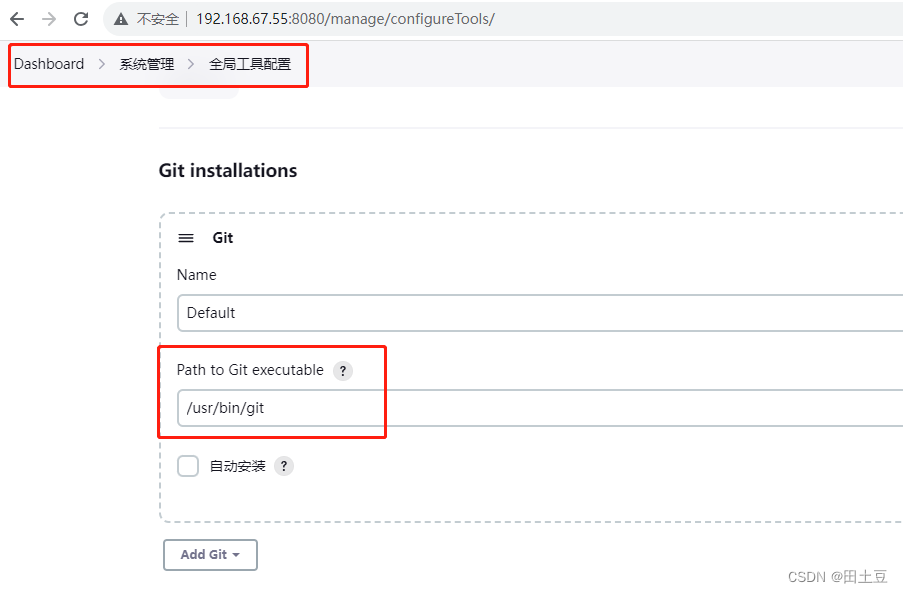
在这里插入图片描述

问题2. 构建任务，控制台报错： ERROR: Couldn’t find any revision to build. Verify the repository and branch configuration for this job.

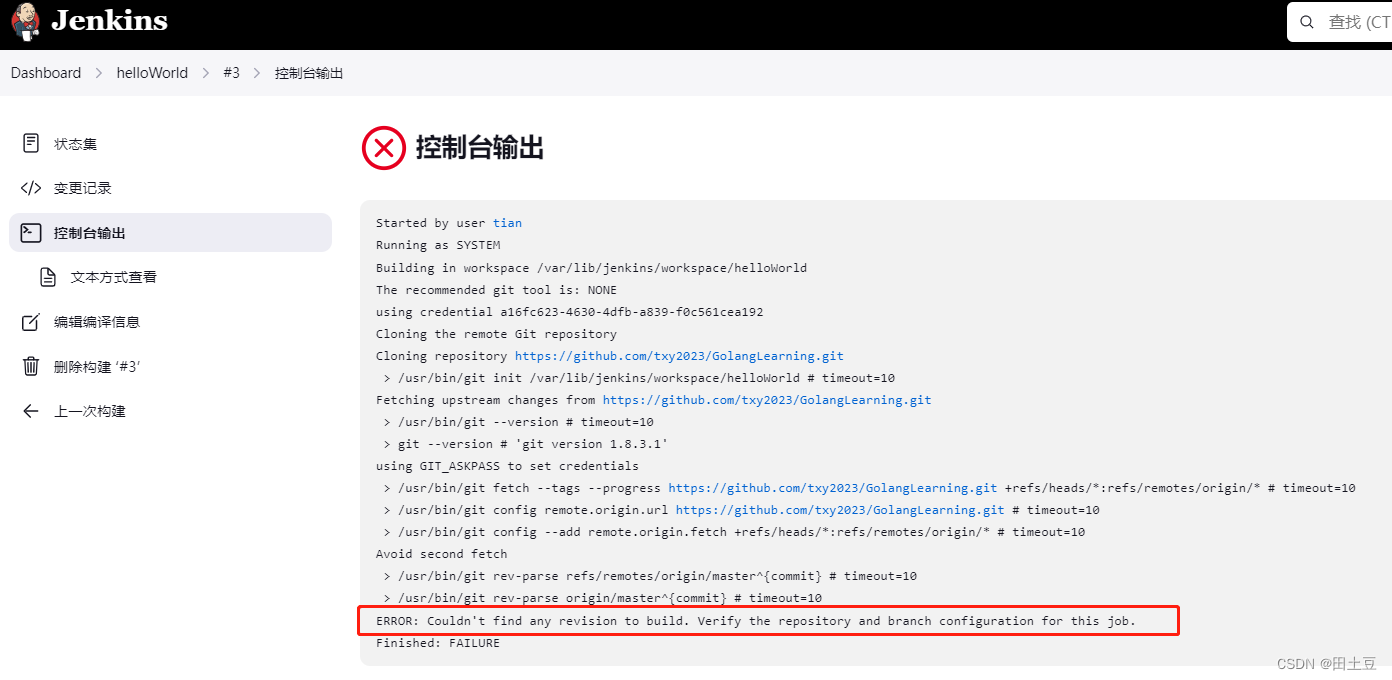
在这里插入图片描述
原因：
拉取的分支不对，git项目默认分支一般是main，而jenkins默认拉取分支是master，因此在源码管理处修改指定分支即可
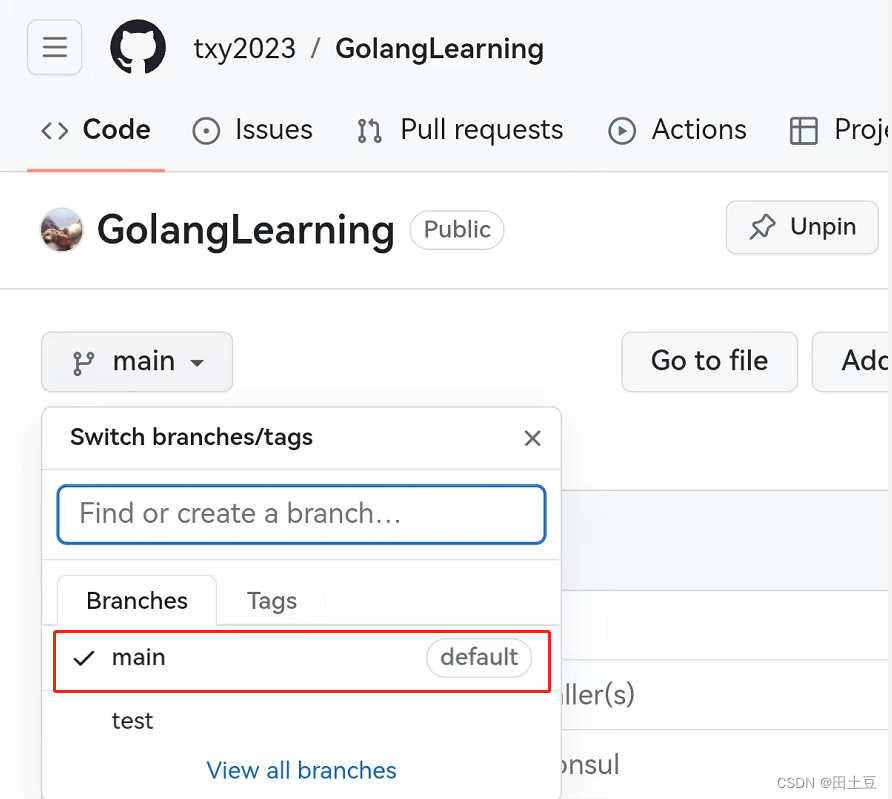
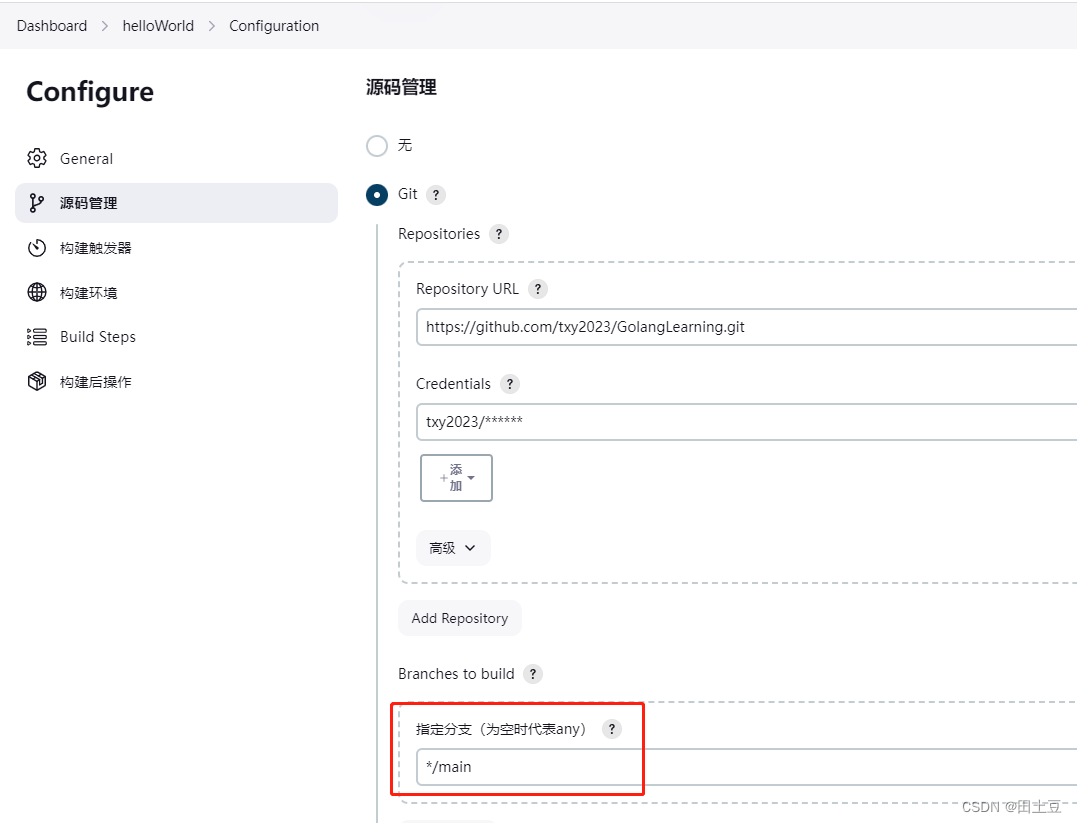
在这里插入图片描述
在这里插入图片描述
修改后，再次构建，成功拉取git项目，默认保存路径为/var/lib/jenkins/workspace/xxx

问题3. 源码管理处填入Repository URL，报错：stderr: Host key verification failed. fatal: Could not read from remote repository.

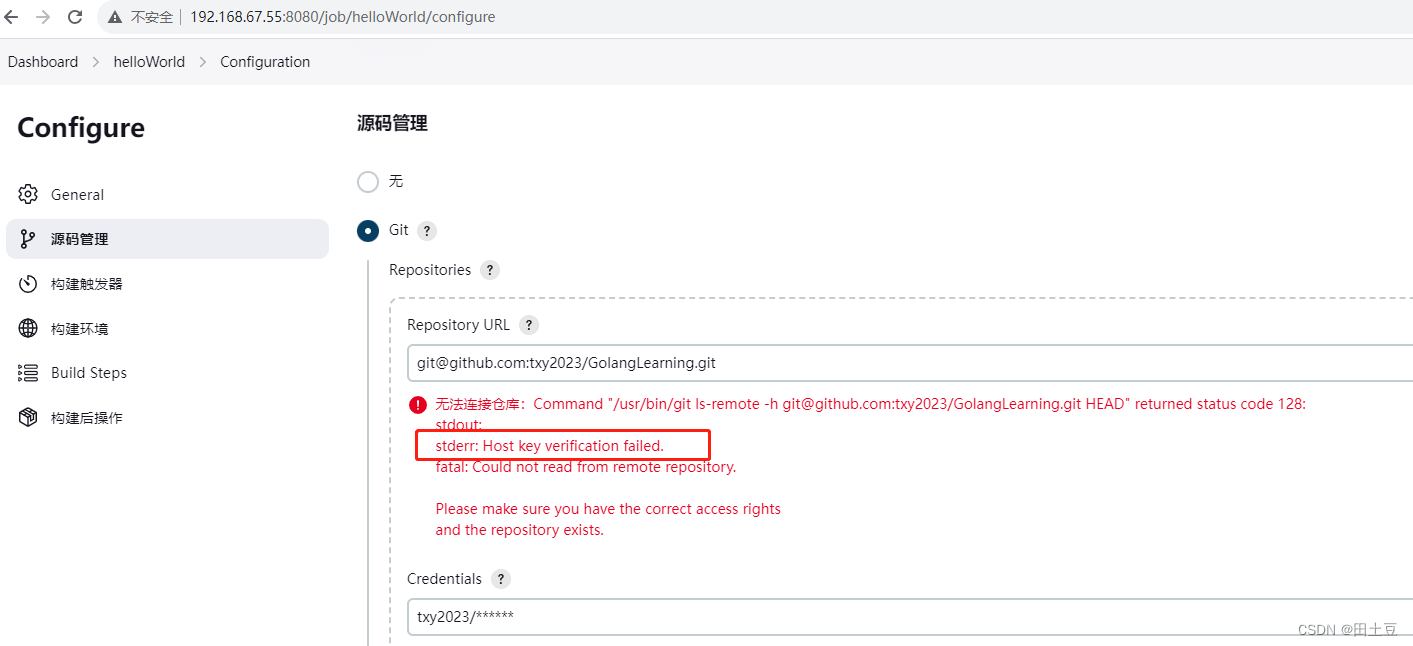
在这里插入图片描述
原因：

  1. github上没有添加SSH key
  2. github上添加的SSH key不对，jenkins拉取源码时默认使用的是jenkins用户
    具体方法：
  • 切换到jenkins用户，生成ssh公钥
 su -s /bin/sh jenkinsssh-keygen

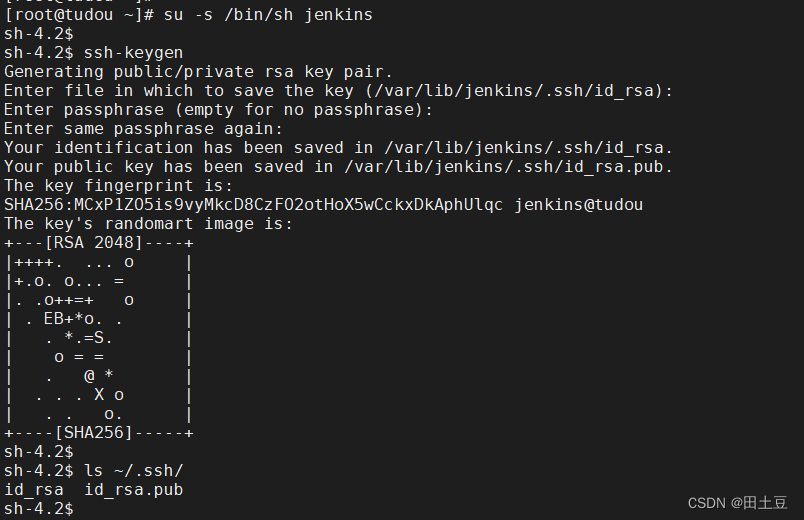
在这里插入图片描述

  • 根据生成的id_rsa.pub文件，在github上重新添加SSH Key
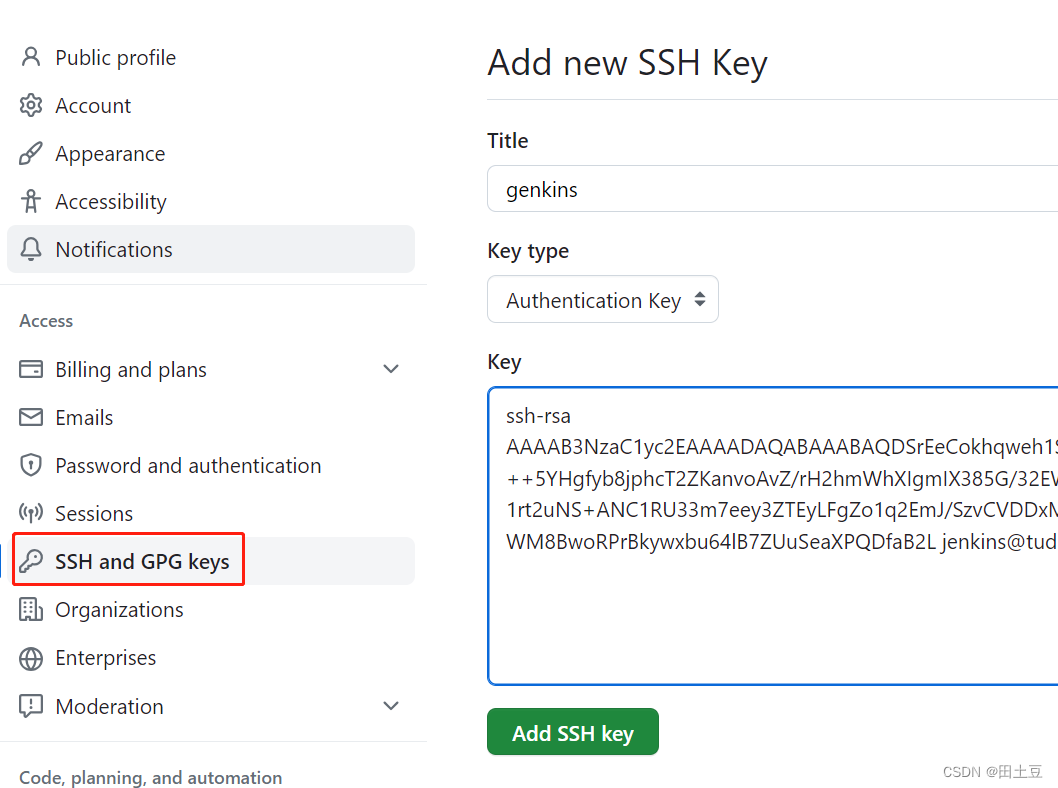
    在这里插入图片描述
  • 最重要的一步，在jenkins用户下，手动执行一次Command/usr/bin/git ls-remote -h git@github.com:txy2023/GolangLearning.git HEAD（根据报错页面上实际的Command执行），目的是自动生成~/.ssh/known_hosts
    在这里插入图片描述

相关文章：

【Jenkins】新建任务FAQ

问题1. 源码管理处填入Repository URL，报错：无法连接仓库：Error performing git command: ls-remote -h https://github.com/txy2023/GolangLearning.git HEAD 原因： jenkins全局工具配置里默认没有添加git的路径，如果…...

编程日记 2023/10/31 20:51:17

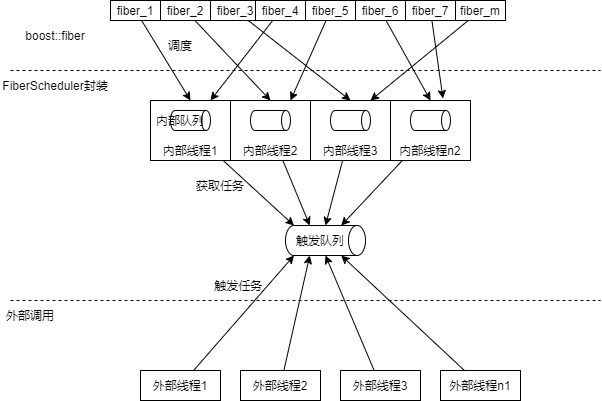
生产环境使用boost::fiber

简介 boost::fiber是一类用户级线程，也就是纤程。其提供的例子与实际生产环境相距较远，本文将对其进行一定的改造，将其能够投入到生产环境。 同时由于纤程是具有传染性的，使用纤程的代码里也全部要用纤程封装，本文将对…...

编程日记 2023/10/31 20:49:14

TSINGSEE青犀AI视频识别技术+危化安全生产智慧监管方案

一、背景分析 石油与化学工业生产过程复杂多样，涉及的物料易燃易爆、有毒有害，生产条件多高温高压、低温负压，现场危险化学品存储量大、危险源集中，重特大安全事故多发。打造基于工业互联网的安全生产新型能力，提高危…...

编程日记 2023/10/31 20:48:13

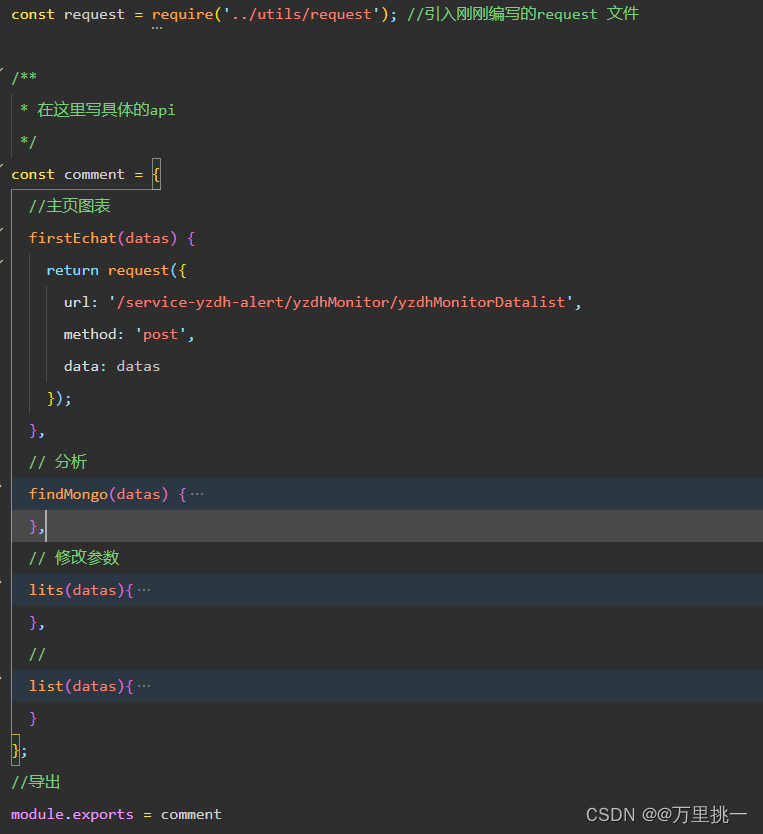
小程序request请求封装

以上为本人的项目目录 1.首先在utils中创建request.js文件封装request请求，此封装带上了token，每次请求都会自带token，需要你从后端获取后利用wx.setStorageSync(token,返回的token),不使用的话就是空。 直接复制即可，需要改一下…...

编程日记 2023/10/31 20:47:12

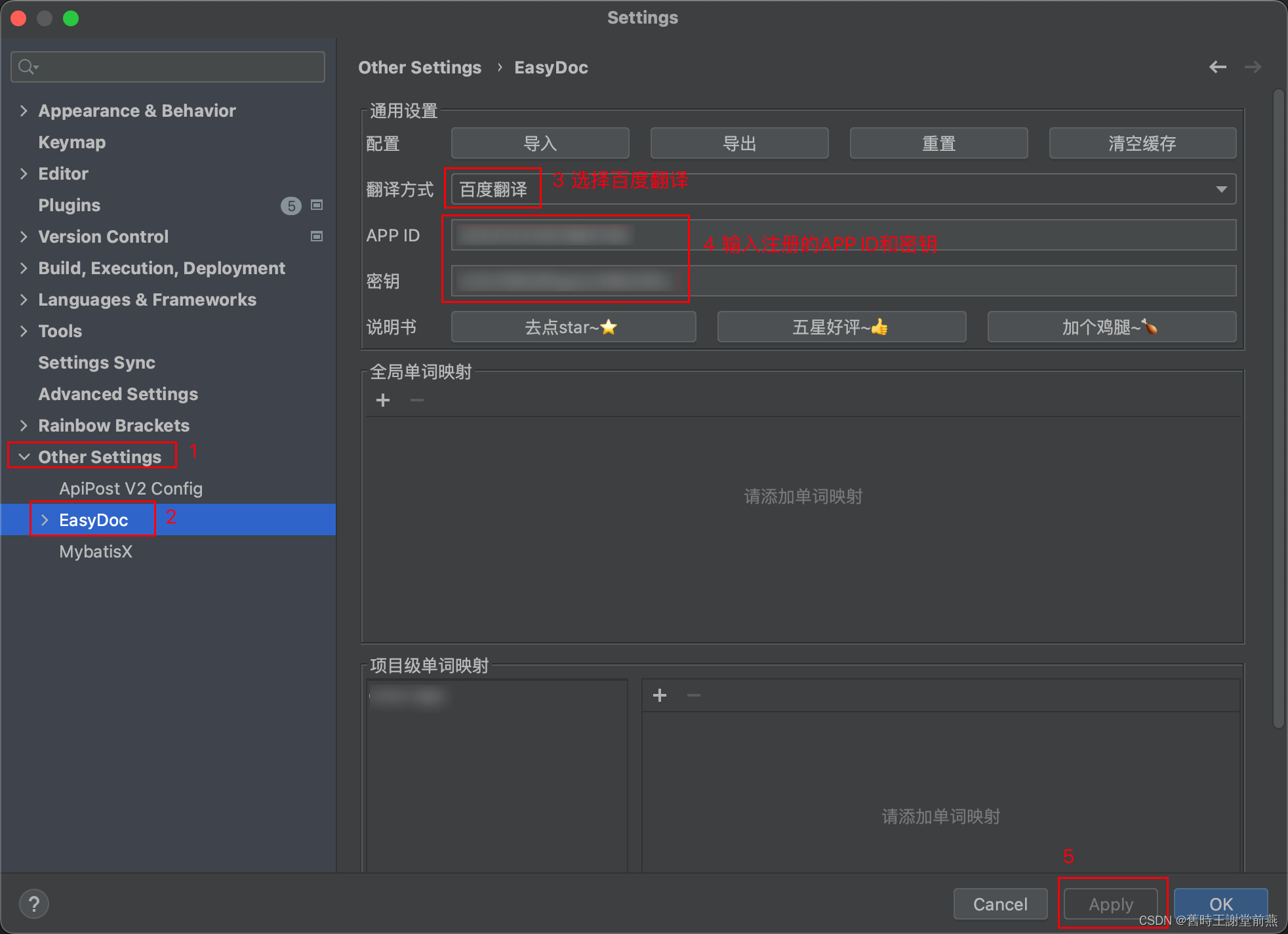
Easy Javadoc插件的使用教程

目录 一、安装Easy Javadoc插件 二、配置注释模板 三、配置翻译 一、安装Easy Javadoc插件 在idea的File-Settings-Plugins中搜索Easy Javadoc插件，点击install进行安装，安装完成后需要restart IDE，重启后插件生效。 二、配置注释模板 …...

编程日记 2023/10/31 20:46:11

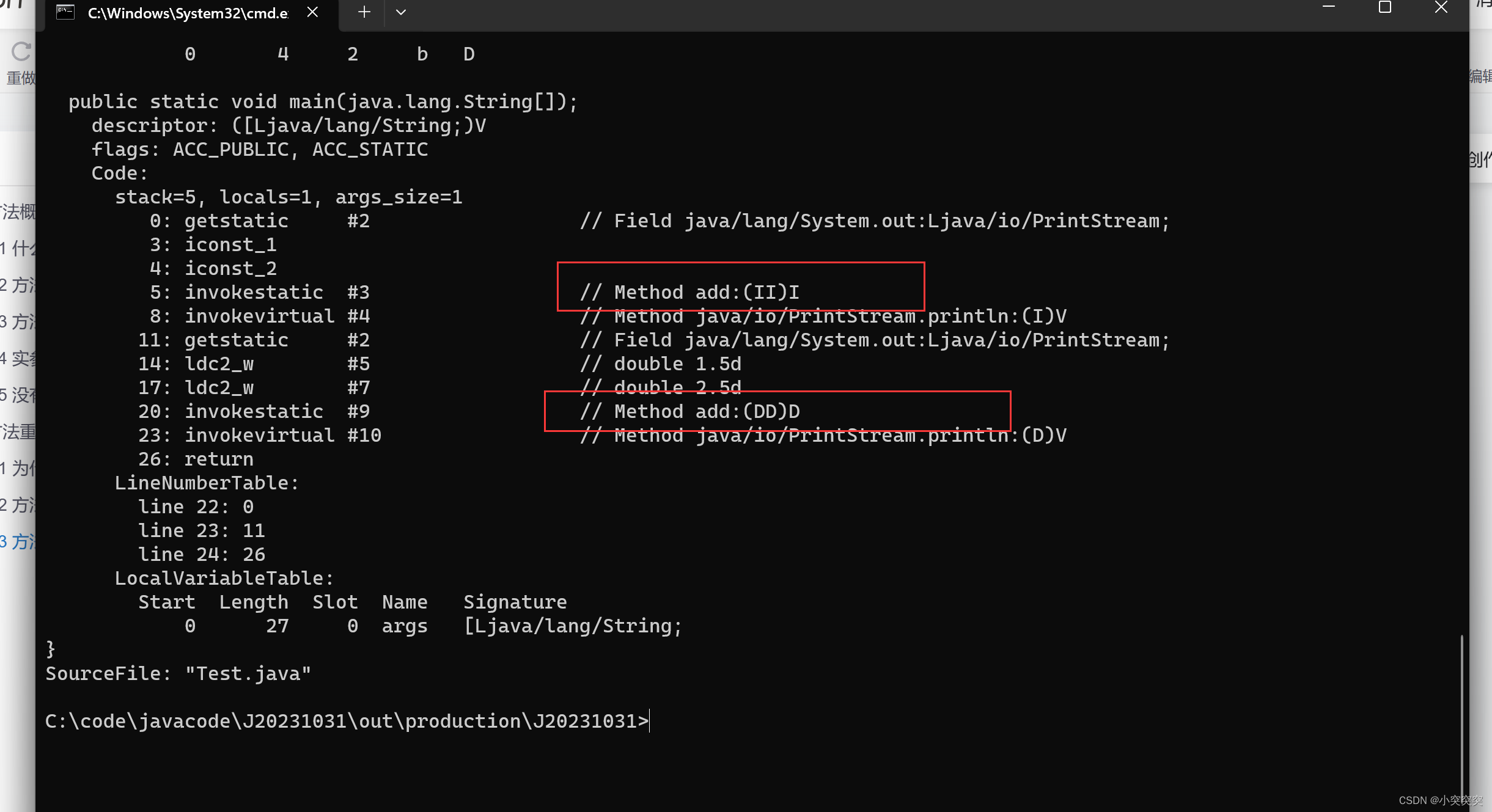
一篇文章让你弄懂Java中的方法

目录 1. 方法概念及使用 1.1 什么是方法(method) 1.2 方法定义 1.3 方法调用的执行过程 1.4 实参和形参的关系 1.5 没有返回值的方法 2. 方法重载 2.1 为什么需要方法重载 2.2 方法重载概念 2.3 方法签名 1. 方法概念及使用 1.1 什么是方法(method) 方法就是一…...

编程日记 2023/10/31 20:45:10

SAP MM学习笔记39 - MRP(资材所要量计划)

这一章开始，离开请求书，学点儿新知识啦。 MRP ( Material Requirement Planning ) - 资材所要量计划。 它的位置在下面的调达周期图上来看，就是右上角的 所要量决定那块儿。 1，MRP(资材所要量计划) 的概要 MRP 的主要目的就是 确…...

编程日记 2023/10/31 20:44:09

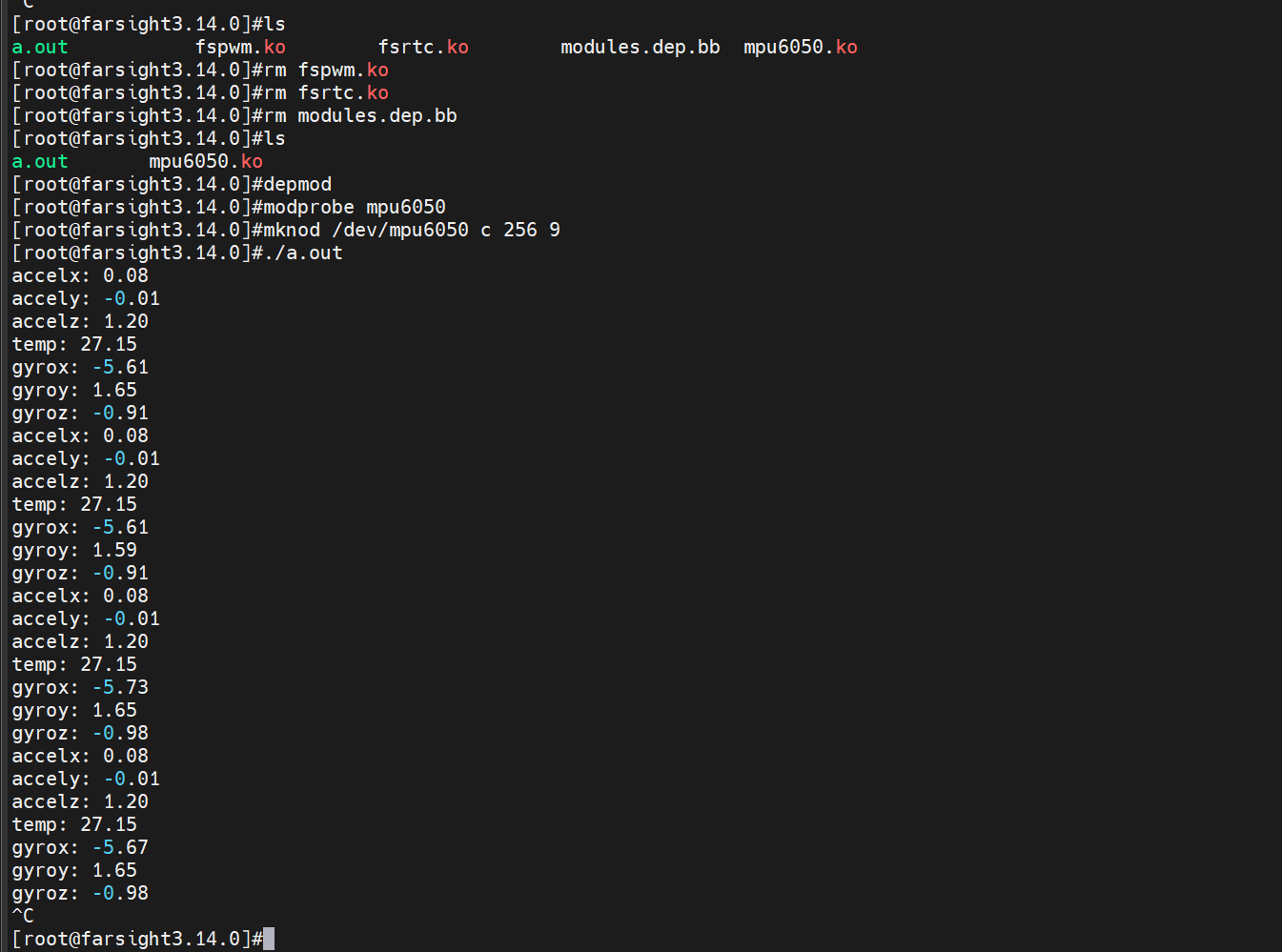
总线类设备驱动——IIC

目录 一、本章目标 二、IIC设备驱动 2.1 I2C协议简介 2.2 LinuxI2C驱动 2.3 I2C 设备驱动实例 一、本章目标 一条总线可以将多个设备连接在一起，提高了系统的可扩展性能。这个互联的系统通常由三部分组成:总线控制器、物理总线(一组信号线) 和设备。总线控制器…...

编程日记 2023/10/31 20:43:08

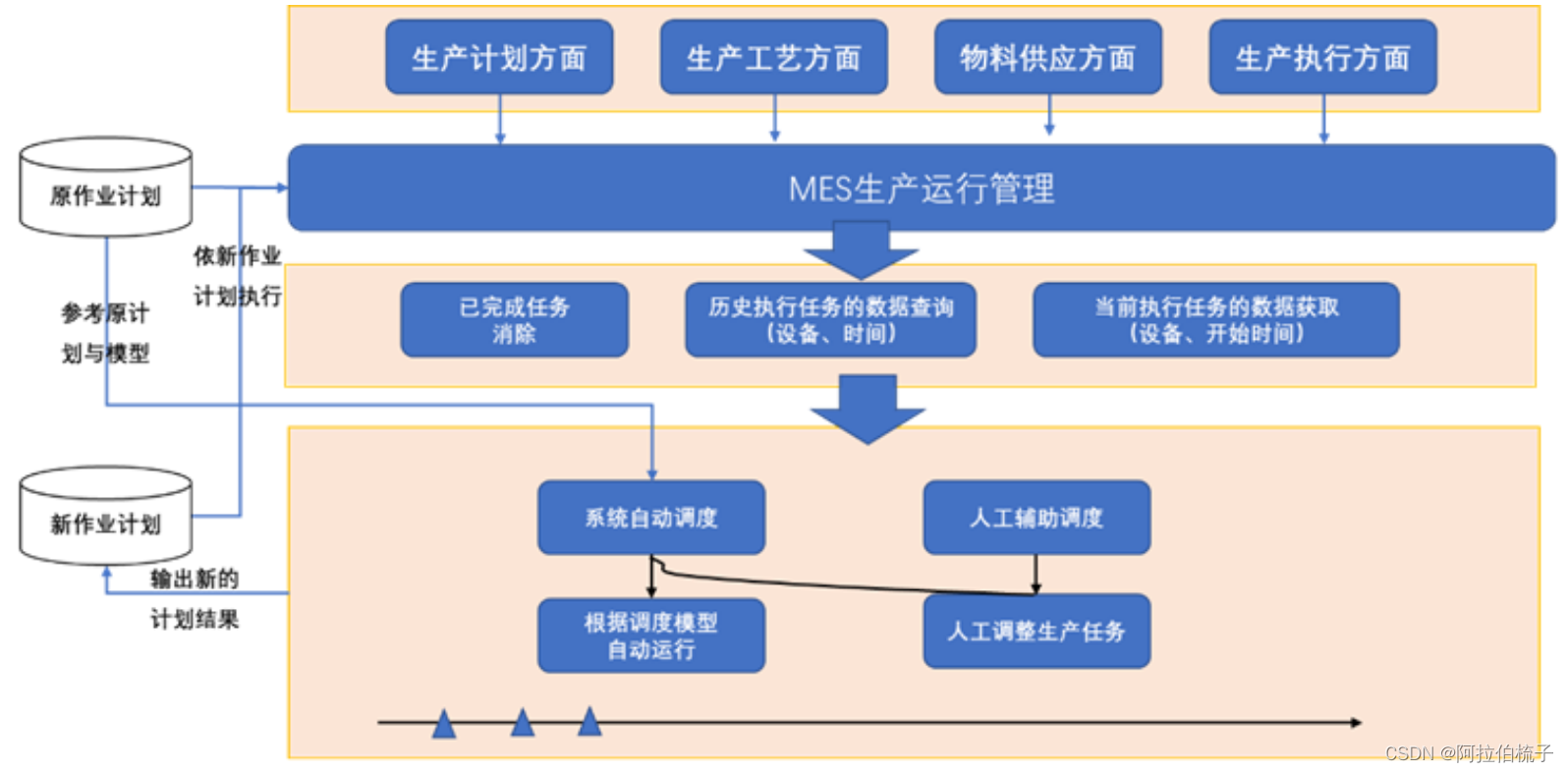
MES 的价值点之动态调度

随着数字化技术的发展，为制造企业的生产计划提供了更多的便利。但在实际生产管理过程中，企业的生产计划不管做的多么理想，还是可能会因诸多的扰动因素造成执行与计划差异，这时就需要通过一些动态调整方案去适应新的生产要求与环境…...

编程日记 2023/10/31 20:42:06

dfs序及相关例题

常用的三种dfs序 欧拉序 每经过一次该点记录一次的序列。 dfs序 记录入栈和出栈的序列。 dfn序 只记录入栈的序列。 dfs序 DFS 序列是指 DFS 调用过程中访问的节点编号的序列。 如何求dfs序&#xff1f;可以用以下代码来找dfs序。 vector<vector<int>> g(n…...

编程日记 2023/10/31 20:41:05

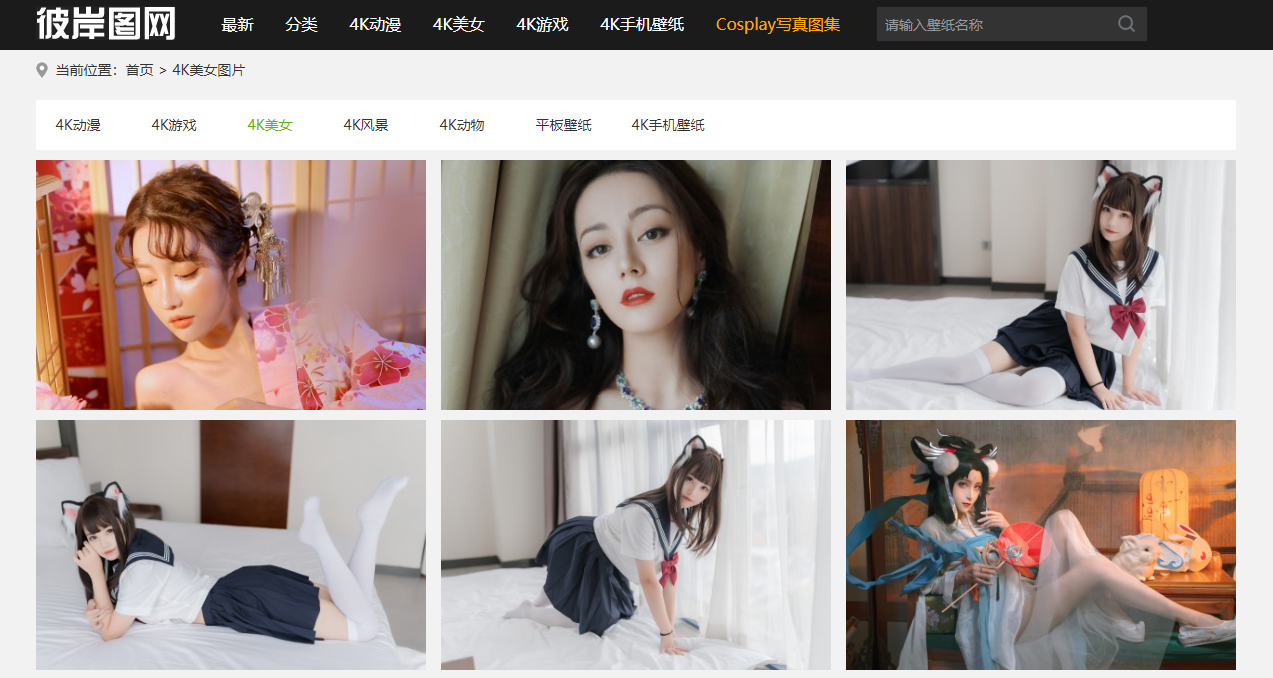
python入门实战:爬取图片到本地

简单记录一下爬取网站图片保存到本地指定目录过程,希望对刚入门的小伙伴有所帮助! 目标网站就是下图所示页面: 实现步骤: 1.爬取每页的图片地址集合 2.下载图片到本地 3. 获取指定页数的页面路径 以下是实现代码: import bs4 import requests import os # 下…...

编程日记 2023/10/31 20:40:04

day02 矩阵 2023.10.26

1.矩阵 2.矩阵乘法 3.特殊矩阵 4.逆矩阵 5.正交矩阵 6.几何意义 7.齐次坐标 8.平移矩阵 9.旋转矩阵 10.缩放矩阵 11.复合运算...

编程日记 2023/10/31 20:39:01

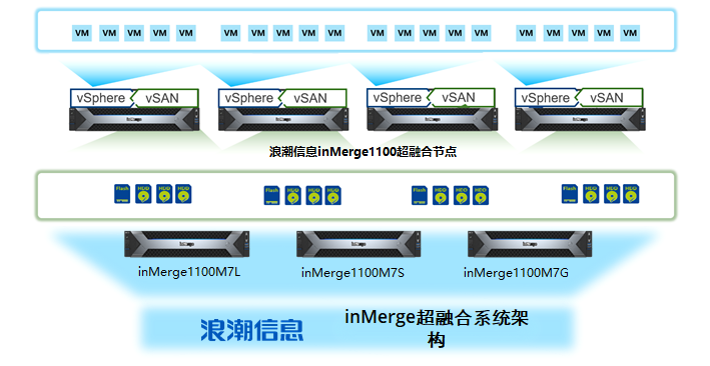
浪潮信息inMerge超融合 刷新全球vSAN架构虚拟化VMmark最佳成绩

近日&#xff0c;在国际权威的VMmark测试中&#xff0c;浪潮信息inMerge1100超融合产品搭载NF5280M7服务器&#xff0c;满载运行44Tiles取得40.95分的成绩&#xff0c;刷新了vSAN架构&#xff08;Intel双路最新平台&#xff09;虚拟化性能测试纪录。该测试结果证明inMerge1100可…...

编程日记 2023/10/31 20:38:00

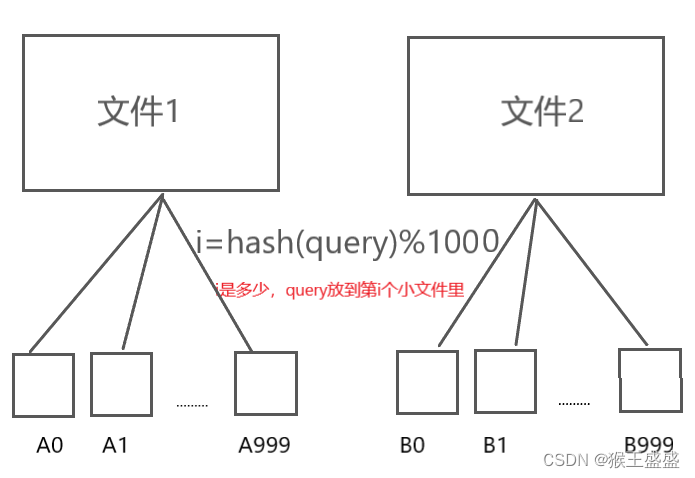
【【哈希应用】位图/布隆过滤器】

位图/布隆过滤器 位图位图概念位图的使用位图模拟实现 布隆过滤器布隆过滤器概念布隆过滤器的使用布隆过滤器模拟实现 位图/布隆过滤器应用&#xff1a;海量数据处理哈希切分 位图 位图概念 计算机中通常以位bit为数据最小存储单位&#xff0c;只有0、1两种二进制状态&#x…...

编程日记 2023/10/31 20:36:59

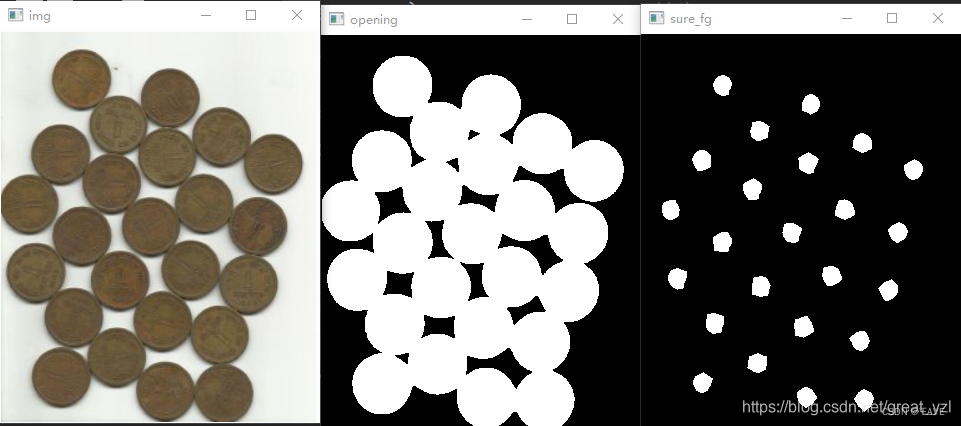
OpenCV学习笔记

一、OpenCV基础 &#xff08;一&#xff09;图像的读取、显示、创建 https://mp.weixin.qq.com/s?__bizMzA4MTA1NjM5NQ&mid2247485202&idx1&sn05d0b4cd25675a99357910a5f2694508&chksm9f9b80f6a8ec09e03ab2bb518ea6aad83db007c9cdd602c7459ed75c737e380ac9c3…...

编程日记 2023/10/31 20:35:58

idea 一键部署jar包

上传成功...

编程日记 2023/10/31 20:34:56

16、SpringCloud -- 常见的接口防刷限流方式

目录 接口防刷限流方式1：隐藏秒杀地址需求：思路：代码：前端：后端：测试：总结：方式2：图形验证码1、生成图形验证码需求：思路：代码：前端：后端：测试：2、校验验证码需求：思路：代码：...

编程日记 2023/10/31 20:33:55

Typora（morkdown编辑器）的安装包和安装教程

Typora&#xff08;morkdown编辑器&#xff09;的安装包和安装教程 下载安装1、覆盖文件2、输入序列号①打开 typora &#xff0c;点击“输入序列号”&#xff1a;②邮箱一栏中任意填写&#xff08;但须保证邮箱地址格式正确&#xff09;&#xff0c;输入序列号&#xff0c;点击…...

编程日记 2023/10/31 20:32:53

服务器不稳定对网站有什么影响

世界上最远的距离&#xff0c;不是树枝无法相依&#xff0c;而是相互了望的星星&#xff0c;却没有交汇的轨迹。 现代技术的进步&#xff0c;导致了人与人之间距 离的消除&#xff0c;直播行业的快速发展的影响和渗透进如今的日常生活&#xff0c;为人们在遥远的距离相见与互诉…...

编程日记 2023/10/31 20:31:51

py实现surf特征提取

import cv2def main():# 加载图像image1 cv2.imread(image1.jpg, cv2.IMREAD_GRAYSCALE)image2 cv2.imread(image2.jpg, cv2.IMREAD_GRAYSCALE)# 创建SURF对象surf cv2.xfeatures2d.SURF_create()# 检测特征点和描述符keypoints1, descriptors1 surf.detectAndCompute(imag…...

编程日记 2023/10/31 20:28:47

MS39233三个半桥驱动器可兼容TMC6300

MS39233 是一款低压三个半桥驱动器。可兼容 TMC6300&#xff08;功能基本一致&#xff0c;管脚不兼容&#xff09;。它可应用于低电压及电池供电的运动控制场合。并且内置电荷泵来提供内部功率 NMOS 所需的栅驱动电压。 MS39233 可以提供最高 2.8A 的峰值电流&#xff0c;其功率…...

编程日记 2023/10/31 20:27:46

09、SpringCloud -- 利用redis的原子性控制高并发请求访问到service层、本地标识

目录 利用redis的原子性控制请求问题：需求：思路什么是原子性的操作？代码思路：代码：工具类依赖SeckillGoodControllerSeckillOrderInfoController测试：本地标识的分析和实现问题：需求：思路：代码：测试：利用redis的原子性控制请求 利用redis的原子性控制人数请求访问到…...

编程日记 2023/10/31 20:26:45

竞赛选题 深度学习图像修复算法 - opencv python 机器视觉

文章目录 0 前言2 什么是图像内容填充修复3 原理分析3.1 第一步&#xff1a;将图像理解为一个概率分布的样本3.2 补全图像 3.3 快速生成假图像3.4 生成对抗网络(Generative Adversarial Net, GAN) 的架构3.5 使用G(z)生成伪图像 4 在Tensorflow上构建DCGANs最后 0 前言 &#…...

编程日记 2023/10/31 20:24:43

基于深度学习网络的美食检测系统matlab仿真

目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 % 图像大小 image_size [224 224 3]; num_classes size(VD,2)-1;% 目标类别数量…...

编程日记 2023/10/31 20:23:42

人工智能基础_机器学习006_有监督机器学习_正规方程的公式推导_最小二乘法_凸函数的判定---人工智能工作笔记0046

我们来看一下公式的推导这部分比较难一些, 首先要记住公式,这个公式,不用自己理解,知道怎么用就行, 比如这个(mA)T 这个转置的关系要知道 然后我们看这个符号就是求X的导数,X导数的转置除以X的导数,就得到单位矩阵, 可以看到下面也是,各种X的导数,然后计算,得到对应的矩阵结…...

编程日记 2023/10/31 20:22:41

【MongoDB】Windows 安装MongoDB 6.0

一、下载安装包 安装包下载地址https://www.mongodb.com/try/download/community这里我选择的是 二、解压并安装 1、解压 这里我将压缩包解压到了D盘&#xff0c;并重命名成了mongodb&#xff0c;解压后的目录如下&#xff1a; 2、创建配置文件 在D:\mongodb下新建conf目录…...

编程日记 2023/10/31 20:20:39

DM8 Dokcer镜像更新后远程无法jdbc连接问题

背景&#xff1a;原来官网下的dm8docker镜像有效期只有两个星期&#xff0c;问他们商务申请了新的dm8镜像&#xff0c;准备简单升级一下镜像再引入原来的database 先说结论&#xff1a;jdbc驱动要更新 官网dm8驱动链接地址 原来的tag镜像 dm8_single:v8.1.2.128_ent_x86_64…...

编程日记 2023/10/31 20:19:37

AI：39-基于深度学习的车牌识别检测

🚀 本文选自专栏：AI领域专栏 从基础到实践，深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家，通过案例和项目实践，掌握核心概念和实用技能。每篇案例都包含代码实例，详细讲解供大家学习。 📌📌📌本专栏包含以下学习方向： 机器学习、深度学…...

编程日记 2023/10/31 20:18:36

软考 系统架构设计师系列知识点之系统架构评估（1）

所属章节&#xff1a; 第8章. 系统质量属性与架构评估 第2节. 系统架构评估 1. 概述 系统架构评估是在对架构分析、评估的基础上&#xff0c;对架构策略的选取进行决策。它利用数学或逻辑分析技术&#xff0c;针对系统的一致性、正确性、质量属性、规划结果等不同方面&#x…...

编程日记 2023/10/31 20:17:35

Spark UI中Shuffle dataSize 和shuffle bytes written 指标区别

背景 本文基于Spark 3.1.1 目前在做一些知识回顾的时候&#xff0c;发现了一些很有意思的事情&#xff0c;就是Spark UI中ShuffleExchangeExec 的dataSize和shuffle bytes written指标是不一样的&#xff0c; 那么在AQE阶段的时候&#xff0c;是以哪个指标来作为每个Task分区大…...

编程日记 2023/10/31 20:15:32