dfs序及相关例题
常用的三种dfs序
- 欧拉序
每经过一次该点记录一次的序列。
- dfs序
记录入栈和出栈的序列。
- dfn序
只记录入栈的序列。
dfs序
DFS 序列是指 DFS 调用过程中访问的节点编号的序列。

如何求dfs序?可以用以下代码来找dfs序。
vector<vector<int>> g(n+1);for(int i = 1; i < n; ++i) {// u,v 建图int u,v; u = fread(); v = fread();g[u].push_back(v);g[v].push_back(u);}// dfs序的左右端点// 表示以x为根的子树的左右端点位置vector<int> l(n + 1), r(n + 1);int cnt = 0;// 一个dfs找dfs序auto dfs = [&](auto &&self, int u, int fa) -> void {l[u] = ++cnt;for(auto y: g[u]) {if(y == fa) continue;self(self, y,u);}r[u] = cnt;};dfs(dfs, k,-1);
一道简单的dfs序的问题。
题目链接:求和 (nowcoder.com)
问题描述:n个节点,n - 1条边,根节点为k。现在又m个操作。
1 a x:将节点a的权值加上x2 a:求a节点的子树上所有节点的和(包括a节点本身)
思路,发现以a为根的子树权值和是一个非线性的,不能用树状数组或者线段树来做。但是dfs序却有一个天然的顺序可以来处理。

观察上图:
-
以5为根的子树序列在dfs序中的排序是:
1 2 3 4 5 6 7 8 -
以8为根的子树序列在dfs序中的排序是:
2 3 -
以2为根的子树序列在dfs序中的排序是:
3 -
以1为根的子树序列在dfs序中的排序是:
4 5 6 7 8
…
我们发现,每个子树都对应 DFS 序列中的连续一段(一段区间)。
DFS(图论) - OI Wiki (oi-wiki.org)
因此本题思路就是:用dfs序将非序列顺序转线性序列。之后就是单点修改,区间查询,可以用树状数组或者线段树来进行求解。
本人是用线段树来进行处理的(线段树大法好
AC代码:
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <queue>
#include <ctime>
#include <random>
#include <sstream>
#include <numeric>
#include <stdio.h>
#include <functional>
#include <bitset>
#include <algorithm>
using namespace std;// #define Multiple_groups_of_examples
#define int_to_long_long
#define IOS std::cout.tie(0);std::cin.tie(0)->sync_with_stdio(false); // 开IOS,需要保证只使用Cpp io流 *
#define dbgnb(a) std::cout << #a << " = " << a << '\n';
#define dbgtt cout<<" !!!test!!! "<<'\n';
#define rep(i,x,n) for(int i = x; i <= n; i++)#define all(x) (x).begin(),(x).end()
#define pb push_back
#define vf first
#define vs secondtypedef long long LL;
#ifdef int_to_long_long
#define int long long
#endif
typedef pair<int,int> PII;const int INF = 0x3f3f3f3f;
const int N = 2e5 + 21;struct SegTree {static const int N = 1e6 + 21;struct node {int l, r, mi;LL sum,add;}tr[N << 2];int w[N];// 左子树inline int ls(int p) {return p<<1; }// 右子树inline int rs(int p) {return p<<1|1; }// 向上更新void pushup(int u) {tr[u].sum = tr[ls(u)].sum + tr[rs(u)].sum;tr[u].mi = min(tr[ls(u)].mi, tr[rs(u)].mi);}// 向下回溯时,先进行更新void pushdown(int u) { // 懒标记,该节点曾经被修改,但其子节点尚未被更新。auto &root = tr[u], &right = tr[rs(u)], &left = tr[ls(u)];if(root.add) {right.add += root.add; right.sum += (LL)(right.r - right.l + 1)*root.add; right.mi -= root.add;left.add += root.add; left.sum += (LL)(left.r - left.l + 1)*root.add; left.mi -= root.add;root.add = 0;}}// 建树void build(int u, int l, int r) {if(l == r) tr[u] = {l, r, w[r], w[r], 0};else {tr[u] = {l,r}; // 容易忘int mid = l + r >> 1;build(ls(u), l, mid), build(rs(u), mid + 1, r);pushup(u);}}// 修改void modify(int u, int l, int r, int d) {if(tr[u].l >= l && tr[u].r <= r) {tr[u].sum += (LL)(tr[u].r - tr[u].l + 1)*d;tr[u].add += d;}else {pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if(l <= mid) modify(ls(u), l ,r, d);if(r > mid) modify(rs(u), l, r, d);pushup(u);}}// 查询LL query(int u, int l, int r) {if(tr[u].l >= l && tr[u].r <= r) {return tr[u].sum;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;LL sum = 0;if(l <= mid) sum = query(ls(u), l, r);if(r > mid ) sum += query(rs(u), l, r);return sum;}
}tree;
// 当输入数据大于 1e6 时用快读
inline int fread() // 快读
{int x = 0, f = 1; char ch = getchar();while(ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar(); }while(ch >= '0' && ch <= '9') {x = x * 10 + (ch - '0');ch = getchar();}return x * f;
}
void inpfile();
void solve() {// int n,m,k; cin>>n>>m>>k;int n = fread(), m = fread(), k = fread();vector<int> a(n + 1);for(int i = 1; i <= n; ++i) a[i] = fread();vector<vector<int>> g(n+1);for(int i = 1; i < n; ++i) {int u,v; u = fread(); v = fread();g[u].push_back(v);g[v].push_back(u);}vector<int> l(n + 1), r(n + 1);int cnt = 0;auto dfs = [&](auto &&self, int u, int fa) -> void {l[u] = ++cnt;for(auto y: g[u]) {if(y == fa) continue;self(self, y,u);}r[u] = cnt;};dfs(dfs, k,-1);for(int i = 1; i <= n; ++i) tree.w[l[i]] = a[i];tree.build(1,1,n);while(m--) {int opt,x,y; opt = fread();if(opt == 2) {// cin>>x>>y;x = fread();cout<<tree.query(1, l[x], r[x])<<'\n';} else {x = fread(), y = fread();tree.modify(1,l[x],l[x],y);}}
}
#ifdef int_to_long_long
signed main()
#else
int main()
#endif{#ifdef Multiple_groups_of_examplesint T; cin>>T;while(T--)#endifsolve();return 0;
}
void inpfile() {#define mytest#ifdef mytestfreopen("ANSWER.txt", "w",stdout);#endif
}
还有一个好题是这几天cfdiv2的F,这个F是牛客上的一个原题。
牛客:华华和月月种树 (nowcoder.com)
cf:Problem - F - Codeforces
个人题解链接:离线处理 + dfs序 + 区间修改 + 单点查询-CSDN博客
dfs序(基础讲解)-CSDN博客
[树 DFS序 详解完全版]_千杯湖底沙.的博客-CSDN博客
相关文章:

dfs序及相关例题
常用的三种dfs序 欧拉序 每经过一次该点记录一次的序列。 dfs序 记录入栈和出栈的序列。 dfn序 只记录入栈的序列。 dfs序 DFS 序列是指 DFS 调用过程中访问的节点编号的序列。 如何求dfs序?可以用以下代码来找dfs序。 vector<vector<int>> g(n…...
python入门实战:爬取图片到本地
简单记录一下爬取网站图片保存到本地指定目录过程,希望对刚入门的小伙伴有所帮助! 目标网站就是下图所示页面: 实现步骤: 1.爬取每页的图片地址集合 2.下载图片到本地 3. 获取指定页数的页面路径 以下是实现代码: import bs4 import requests import os # 下…...

day02 矩阵 2023.10.26
1.矩阵 2.矩阵乘法 3.特殊矩阵 4.逆矩阵 5.正交矩阵 6.几何意义 7.齐次坐标 8.平移矩阵 9.旋转矩阵 10.缩放矩阵 11.复合运算...
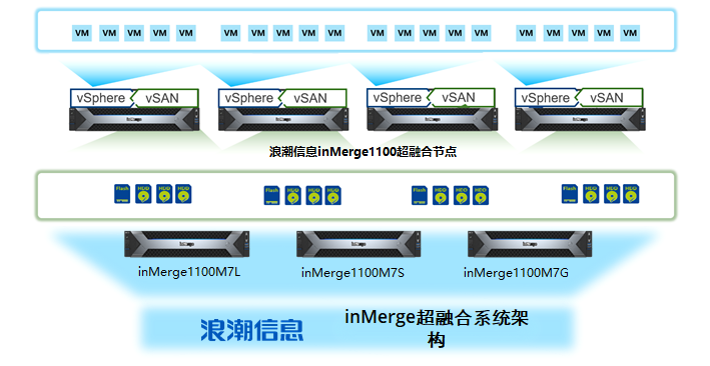
浪潮信息inMerge超融合 刷新全球vSAN架构虚拟化VMmark最佳成绩
近日,在国际权威的VMmark测试中,浪潮信息inMerge1100超融合产品搭载NF5280M7服务器,满载运行44Tiles取得40.95分的成绩,刷新了vSAN架构(Intel双路最新平台)虚拟化性能测试纪录。该测试结果证明inMerge1100可…...
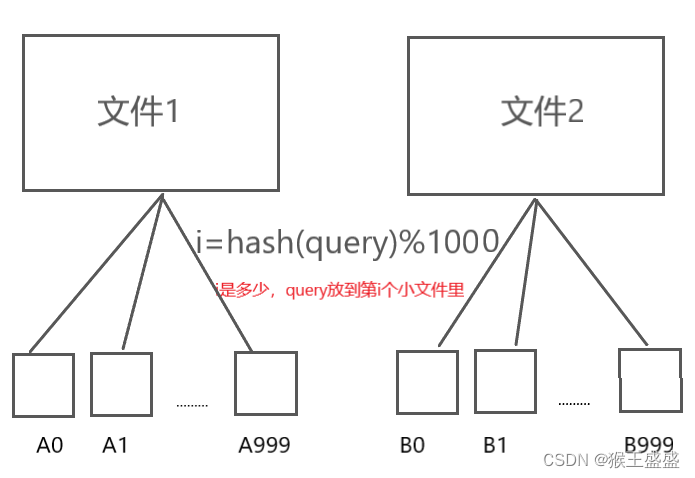
【【哈希应用】位图/布隆过滤器】
位图/布隆过滤器 位图位图概念位图的使用位图模拟实现 布隆过滤器布隆过滤器概念布隆过滤器的使用布隆过滤器模拟实现 位图/布隆过滤器应用:海量数据处理哈希切分 位图 位图概念 计算机中通常以位bit为数据最小存储单位,只有0、1两种二进制状态&#x…...
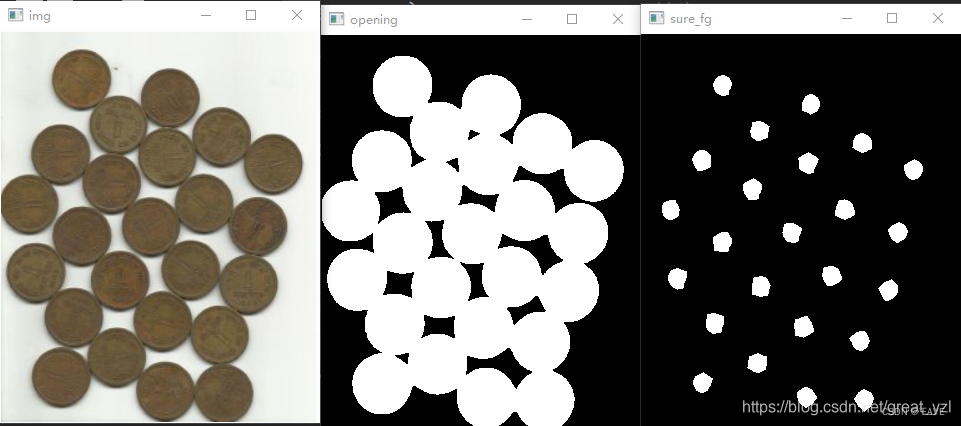
OpenCV学习笔记
一、OpenCV基础 (一)图像的读取、显示、创建 https://mp.weixin.qq.com/s?__bizMzA4MTA1NjM5NQ&mid2247485202&idx1&sn05d0b4cd25675a99357910a5f2694508&chksm9f9b80f6a8ec09e03ab2bb518ea6aad83db007c9cdd602c7459ed75c737e380ac9c3…...
idea 一键部署jar包
上传成功...

16、SpringCloud -- 常见的接口防刷限流方式
目录 接口防刷限流方式1:隐藏秒杀地址需求:思路:代码:前端:后端:测试:总结:方式2:图形验证码1、生成图形验证码需求:思路:代码:前端:后端:测试:2、校验验证码需求:思路:代码:...
Typora(morkdown编辑器)的安装包和安装教程
Typora(morkdown编辑器)的安装包和安装教程 下载安装1、覆盖文件2、输入序列号①打开 typora ,点击“输入序列号”:②邮箱一栏中任意填写(但须保证邮箱地址格式正确),输入序列号,点击…...

服务器不稳定对网站有什么影响
世界上最远的距离,不是树枝无法相依,而是相互了望的星星,却没有交汇的轨迹。 现代技术的进步,导致了人与人之间距 离的消除,直播行业的快速发展的影响和渗透进如今的日常生活,为人们在遥远的距离相见与互诉…...

py实现surf特征提取
import cv2def main():# 加载图像image1 cv2.imread(image1.jpg, cv2.IMREAD_GRAYSCALE)image2 cv2.imread(image2.jpg, cv2.IMREAD_GRAYSCALE)# 创建SURF对象surf cv2.xfeatures2d.SURF_create()# 检测特征点和描述符keypoints1, descriptors1 surf.detectAndCompute(imag…...
MS39233三个半桥驱动器可兼容TMC6300
MS39233 是一款低压三个半桥驱动器。可兼容 TMC6300(功能基本一致,管脚不兼容)。它可应用于低电压及电池供电的运动控制场合。并且内置电荷泵来提供内部功率 NMOS 所需的栅驱动电压。 MS39233 可以提供最高 2.8A 的峰值电流,其功率…...

09、SpringCloud -- 利用redis的原子性控制高并发请求访问到service层、本地标识
目录 利用redis的原子性控制请求问题:需求:思路什么是原子性的操作?代码思路:代码:工具类依赖SeckillGoodControllerSeckillOrderInfoController测试:本地标识的分析和实现问题:需求:思路:代码:测试:利用redis的原子性控制请求 利用redis的原子性控制人数请求访问到…...
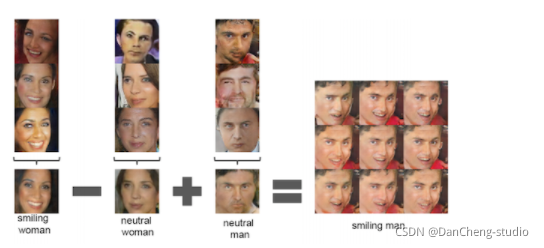
竞赛选题 深度学习图像修复算法 - opencv python 机器视觉
文章目录 0 前言2 什么是图像内容填充修复3 原理分析3.1 第一步:将图像理解为一个概率分布的样本3.2 补全图像 3.3 快速生成假图像3.4 生成对抗网络(Generative Adversarial Net, GAN) 的架构3.5 使用G(z)生成伪图像 4 在Tensorflow上构建DCGANs最后 0 前言 &#…...

基于深度学习网络的美食检测系统matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 % 图像大小 image_size [224 224 3]; num_classes size(VD,2)-1;% 目标类别数量…...

人工智能基础_机器学习006_有监督机器学习_正规方程的公式推导_最小二乘法_凸函数的判定---人工智能工作笔记0046
我们来看一下公式的推导这部分比较难一些, 首先要记住公式,这个公式,不用自己理解,知道怎么用就行, 比如这个(mA)T 这个转置的关系要知道 然后我们看这个符号就是求X的导数,X导数的转置除以X的导数,就得到单位矩阵, 可以看到下面也是,各种X的导数,然后计算,得到对应的矩阵结…...
【MongoDB】Windows 安装MongoDB 6.0
一、下载安装包 安装包下载地址https://www.mongodb.com/try/download/community这里我选择的是 二、解压并安装 1、解压 这里我将压缩包解压到了D盘,并重命名成了mongodb,解压后的目录如下: 2、创建配置文件 在D:\mongodb下新建conf目录…...

DM8 Dokcer镜像更新后远程无法jdbc连接问题
背景:原来官网下的dm8docker镜像有效期只有两个星期,问他们商务申请了新的dm8镜像,准备简单升级一下镜像再引入原来的database 先说结论:jdbc驱动要更新 官网dm8驱动链接地址 原来的tag镜像 dm8_single:v8.1.2.128_ent_x86_64…...

AI:39-基于深度学习的车牌识别检测
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌本专栏包含以下学习方向: 机器学习、深度学…...
)
软考 系统架构设计师系列知识点之系统架构评估(1)
所属章节: 第8章. 系统质量属性与架构评估 第2节. 系统架构评估 1. 概述 系统架构评估是在对架构分析、评估的基础上,对架构策略的选取进行决策。它利用数学或逻辑分析技术,针对系统的一致性、正确性、质量属性、规划结果等不同方面&#x…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
