当前位置： 首页 > news >正文

JVM虚拟机：堆结构的逻辑分区

news 2026/2/10 0:50:19

堆内存的逻辑分区

堆内存的逻辑分区如下所示：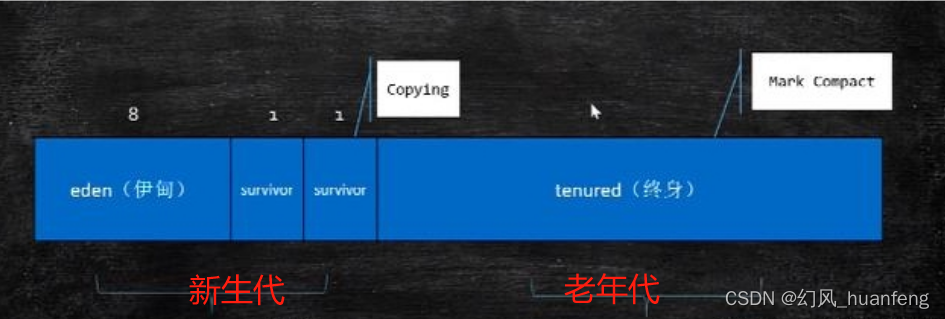

堆内存中分为新生代和老年代，二者空间大小1：3。在新生代里面分为两类区域（eden、survivor），三个区域（eden、survivor、survivor），三个区大小比例为8：1：1。

对象存放的位置

栈

当我们new一个对象的时候，首先会将对象分配到栈上（线程私有小对象、无逃逸（方法外没有引用指向这个对象）、支持标量替换（类的成员变量就可以表示这个类）、无需调整），如果分配不了才会分配到eden区（对象大的时候就会分配不了，多少算大？有参数控制）。

新生代

在eden区有一个叫做线程本地分配TLAB的概念，因为多线程访问eden的时候需要保证安全，那么必然效率降低，此时我们可以让每个线程占用eden的1%的空间，然后对于每个线程来说，这个空间都是私有的，多线程的时候不用竞争就可以使用这个空间，可以提高效率。

还有一个动态年龄的概念，当年轻代进行垃圾回收的时候，假如是从eden+s0到s1的空间，如果此时eden+s0存活的对象超过了s1空间的一半，那么此时就会将一部分对象直接放到老年代。它会从年纪小的对象开始累加，当加入某个年龄段后，累加和超过survivor区域

相关文章：

JVM虚拟机：堆结构的逻辑分区

堆内存的逻辑分区 堆内存的逻辑分区如下所示： 堆内存中分为新生代和老年代，二者空间大小1：3。在新生代里面分为两类区域（eden、survivor），三个区域（eden、survivor、survivor），三个区大小比例为8：1：1。 对象存放的位置 栈 当我们new一个对象的时候，首先会将对象…...

编程日记 2023/11/1 0:27:10

RabbitMQ学习02

Hello World&#xff08;Java&#xff09; 1.导入依赖 <!--指定 jdk 编译版本--><build><plugins><plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-compiler-plugin</artifactId><configuration&g…...

编程日记 2023/11/1 0:26:08

android中的Package安装、卸载、更新替换流程

android系统在安装&#xff0c;删除&#xff0c;替换&#xff0c;清除数据等与应用相关的动作时&#xff0c;会发出对应的Broadcast&#xff0c;上层的应用通过注册相应的广播事件来做相应的处理。 官方文档中给出了详尽的罗列&#xff1a; ACTION_PACKAGE_ADDED 一个新应用包已…...

编程日记 2023/11/1 0:25:07

思维训练第三课 反意疑问句

系列文章目录 文章目录 系列文章目录前言一、什么是反意疑问句二、反意疑问句的回答&#x1f49a;主系表/主谓宾&#xff08;肯定&#xff09;&#xff0c;否定提问1、一般现在时2、一般过去时3、一般将来时4、现在完成时 &#x1f49b; 主谓宾1、一般现在2、一般过去3、一般将…...

编程日记 2023/11/1 0:24:06

nvm安装步骤

注意事项 不要安装任何版本的node.js&#xff0c;有的话卸载干净&#xff01;注意&#xff1a;要卸载干净了&#xff01; 安装步骤&#xff1a; nvm下载 点击exe文件安装 安装目录选择&#xff1a;D:\NVM 下一步创建nodejs文件放在D:\NVM 下&#xff0c;然后一直next到最后 …...

编程日记 2023/11/1 0:23:05

关于比较级（内含名词比较级）

在比较级中&#xff0c;修饰形容词一般使用more 或者-er的变体&#xff0c;但是怎么修饰名词呢&#xff1f; 即&#xff0c;如果我们想表达&#xff1a;你能不能表现得更马屁精一点&#xff1f;这种针对一个具体名词的程度升级怎么表达呢&#xff1f; 使用be more of 名词的…...

编程日记 2023/11/1 0:22:04

【算法|动态规划 | 线性dp | 最长上升子序列模型No.1】AcWing1017.怪盗基德的滑翔翼 AcWing1014.登山

个人主页&#xff1a;兜里有颗棉花糖 欢迎 点赞&#x1f44d; 收藏✨ 留言✉ 加关注&#x1f493;本文由 兜里有颗棉花糖 原创 收录于专栏【AcWing算法提高学习专栏】 &#x1f354;本专栏旨在提高自己算法能力的同时&#xff0c;记录一下自己的学习过程&#xff0c;希望对大家…...

编程日记 2023/11/1 0:21:03

2023年道路运输企业主要负责人证模拟考试题库及道路运输企业主要负责人理论考试试题

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 2023年道路运输企业主要负责人证模拟考试题库及道路运输企业主要负责人理论考试试题是由安全生产模拟考试一点通提供&#xff0c;道路运输企业主要负责人证模拟考试题库是根据道路运输企业主要负责人最新版教材&#…...

编程日记 2023/11/1 0:20:02

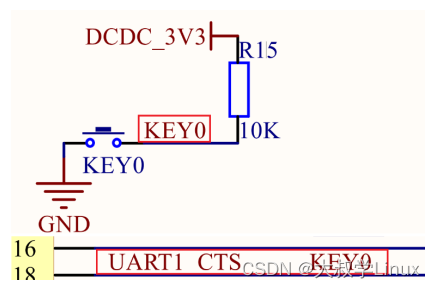
Linux学习第26天：异步通知驱动开发： 主动

Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 在正式开启今天的学习前&#xff0c;讲一讲为什么标题中加入了【主动】俩字。之前学习的阻塞和非阻塞IO&#xff0c;都是在被动的接受应用程序的操作。而今天的学…...

编程日记 2023/11/1 0:18:59

SpringBoot的核心配置：YAML概述、基础语法；JSR303数据校验；多环境切换

SpringBoot核心配置 SpringBoot配置文件分类 SpringBoot是基于约定的&#xff0c;所以很多配置都有默认值&#xff0c;但如果想使用自己的配置替换默认配置的话&#xff0c;就可以使用 application.properties或者application.yml&#xff08;application.yaml&#xff09;进…...

编程日记 2023/11/1 0:17:58

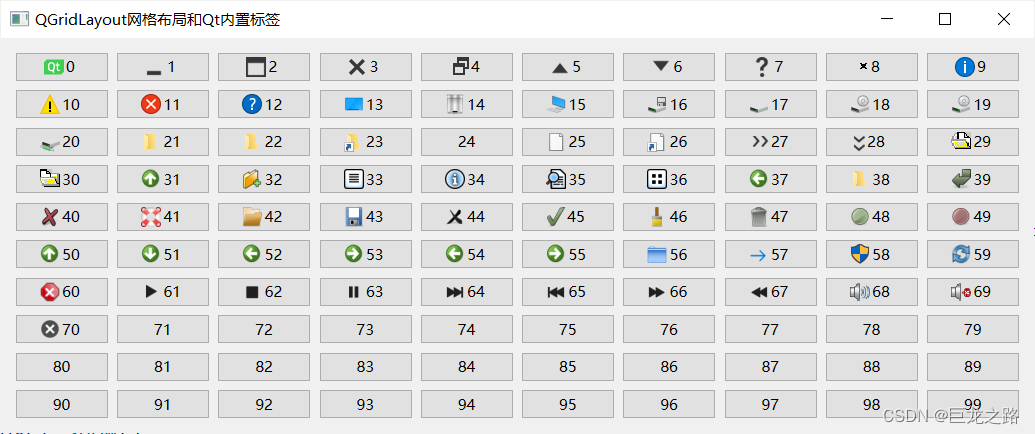
把Qt6.2.4内置的标签打印了一遍

2023年10月31日&#xff0c;周二晚上 #include <QGridLayout> #include <QPushButton> #include <QLabel> #include <QApplication> #include <QStyle>int main(int argc, char *argv[]) {QApplication a(argc, argv);QWidget widget;widget.set…...

编程日记 2023/11/1 0:15:55

element-ui 表单校验・大全

目录 1、对全部表单项的校验2、校验指定字段3、自定义函数校验表单4、一行内多个输入框的校验 element-ui 官网 element-ui 表单校验的规则如下&#xff1a; <属性名>: [{ required: true,// 是否必填&#xff08;若有label则在其左上角显示红点&#xff0c;否则不显示必…...

编程日记 2023/11/1 0:14:54

搭建高性能分布式存储-minio

文章目录 搭建高性能分布式存储-minioDocker搭建minio&#xff08;单机部署纠删码模式&#xff09;⭐创建minio的bucket&#xff08;桶&#xff09;⭐SpringBootminio项目实战 ⭐1&#xff1a;导入minio的maven依赖2&#xff1a;编写MinioProperties.class3&#xff1a;applica…...

编程日记 2023/11/1 0:13:53

leetCode 137. 只出现一次的数字 II（拓展篇） + 模5加法器 + 真值表（数字电路）

leetCode 137. 只出现一次的数字 II 题解可看我的往期文章 leetCode 137. 只出现一次的数字 II 位运算 模3加法器 真值表&#xff08;数字电路&#xff09; 有限状态机-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134138112?spm1001.2014.3001.5501…...

编程日记 2023/11/1 0:12:52

docker导致root空间满进入不了系统解决方案

由于docker建立镜像会产生很多缓存文件&#xff0c;最终导致root目录满&#xff0c;进入不了系统 df -h docker默认路径是在/var/lib/docker下 可以通过命令查看docker占用空间 docker system df 如果占用空间太大 可用以下命令清理 $ docker image prune -h Flag shorth…...

编程日记 2023/11/1 0:11:51

uni-app遮罩遮住小程序tabbar

uni-app遮罩遮住小程序tabbar 1、用uni-app自带的方法显示隐藏 //通过弹窗显隐控制导航栏的显示和隐藏 const popupChange e >{if(e.show){//隐藏tabbaruni.hideTabBar()}else{//显示tabbaruni.showTabBar()}state.searchIcon e.show } //通过弹窗显隐控制导航栏的显示和…...

编程日记 2023/11/1 0:08:47

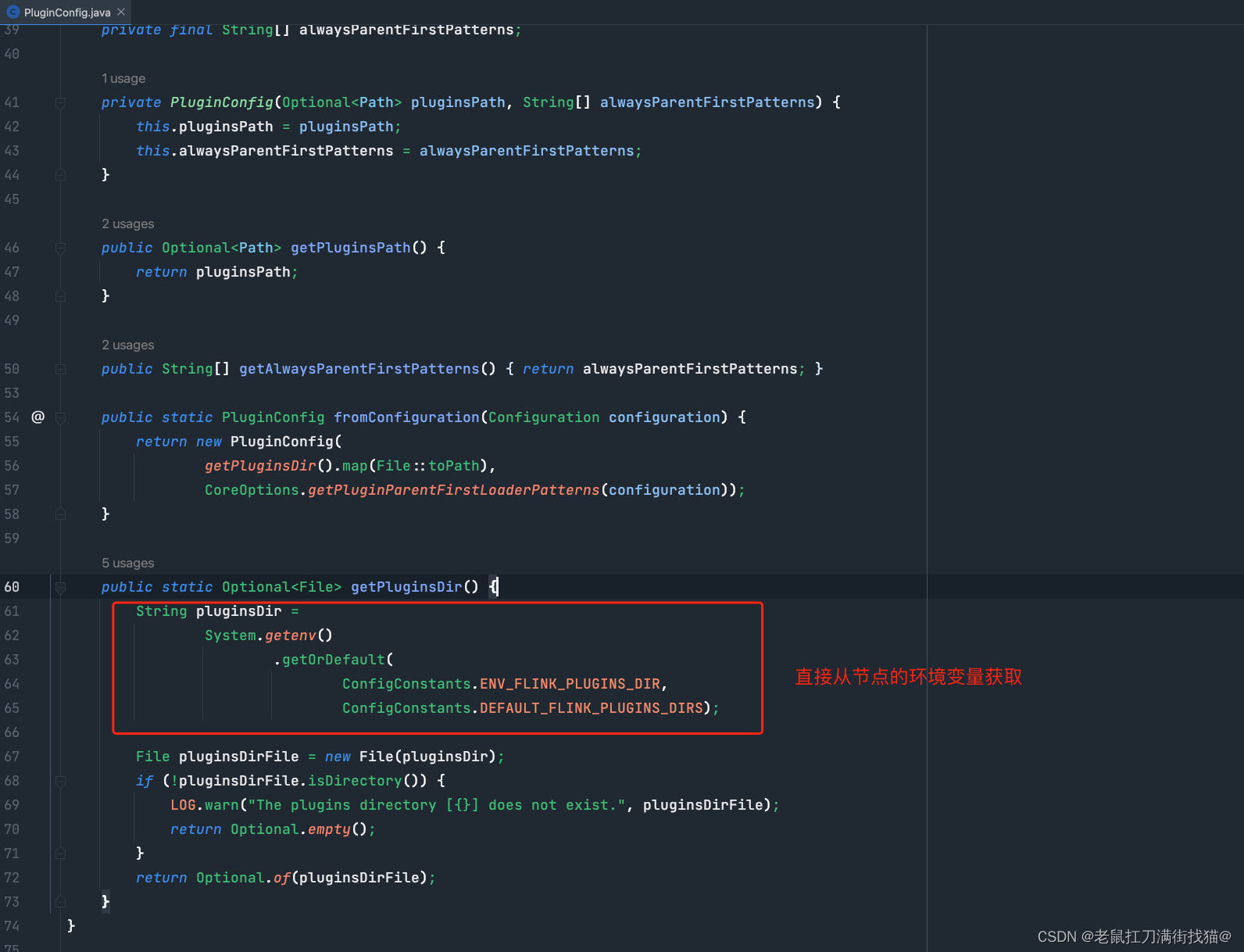
Flink on yarn 加载失败plugins失效问题解决

Flink on yarn 加载失败plugins失效问题解决 flink版本&#xff1a;1.13.6 1. 问题 flink 任务运行在yarn集群,plugins加载失效,导致通过扩展资源获取任务参数失效 2. 问题定位 yarn容器的jar包及插件信息,jar包是正常上传 源码定位 加载plugins入口&#xff0c;TaskMana…...

编程日记 2023/11/1 0:07:46

显卡服务器的特点和优势在哪里

随着科技的发展以及人们对于计算机性能的需求提高&#xff0c;显卡服务器是主要使用图形处理器进行计算和运算&#xff0c;拥有更加强大的计算能力&#xff0c;今天小编就来给大家讲一讲显卡服务器的特点和优势是什么&#xff01; 1.高可靠性&#xff1a;显卡服务器采用高品质的…...

编程日记 2023/11/1 0:06:45

c++设计模式二：原型模式

使用场景&#xff1a;当需要构建多个相同的类对象时&#xff0c;而且该类对象结构较为复杂&#xff0c;如果每个都重新组织构建会很麻烦。 其实&#xff0c;就是写一个拷贝构造函数&#xff0c;或者写一个拷贝每个成员变量的clone()方法。 举例说明&#xff1a;比如一个相亲网站…...

编程日记 2023/11/1 0:05:44

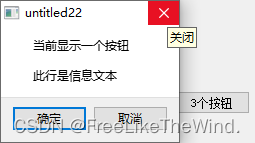
【Qt控件之QMessageBox】详解

Qt控件之QMessageBox 描述基于属性的API富文本和文本格式属性严重程度以及图标和Pixmap属性静态函数API 高级用法默认按钮和退出按钮示例使用场景 描述 QMessageBox类提供了一个模态对话框&#xff0c;用于通知用户或向用户提问并接收答案。 消息框显示一个主要文本以提醒用户…...

编程日记 2023/11/1 0:04:43

java 实现excel文件转pdf | 无水印 | 无限制

文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具，自己手写的难度，恐怕高级程序员花费一年的事件，也…...

编程新知 2025/11/5 4:10:42

Qt Http Server模块功能及架构

Qt Http Server 是 Qt 6.0 中引入的一个新模块&#xff0c;它提供了一个轻量级的 HTTP 服务器实现&#xff0c;主要用于构建基于 HTTP 的应用程序和服务。 功能介绍&#xff1a; 主要功能 HTTP服务器功能&#xff1a; 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

编程新知 2025/10/17 21:16:57

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器

一、原理介绍 传统滑模观测器采用如下结构&#xff1a; 传统SMO中LPF会带来相位延迟和幅值衰减&#xff0c;并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF)&#xff0c;可以去除高次谐波&#xff0c;并且不用相位补偿就可以获得一个误差较小的转子位…...

编程新知 2026/2/7 9:27:22

消息队列系统设计与实践全解析

文章目录 &#x1f680; 消息队列系统设计与实践全解析&#x1f50d; 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡&#x1f4a1; 权衡决策框架 1.3 运维复杂度评估&#x1f527; 运维成本降低策略 &#x1f3d7;️ 二、典型架构设计2.1 分布式事务最终一致…...

编程新知 2026/2/5 4:20:53

ZYNQ学习记录FPGA(一)ZYNQ简介

一、知识准备 1.一些术语,缩写和概念&#xff1a; 1&#xff09;ZYNQ全称&#xff1a;ZYNQ7000 All Pgrammable SoC 2&#xff09;SoC:system on chips(片上系统)&#xff0c;对比集成电路的SoB&#xff08;system on board&#xff09; 3&#xff09;ARM&#xff1a;处理器…...

编程新知 2026/2/5 9:30:45

【安全篇】金刚不坏之身：整合 Spring Security + JWT 实现无状态认证与授权

摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题&#xff1a;安全。文章将详细阐述认证&#xff08;Authentication) 与授权&#xff08;Authorization的核心概念&#xff0c;对比传统 Session-Cookie 与现代 JWT&#xff08;JS…...

编程新知 2025/12/7 16:12:52

软件工程 期末复习

瀑布模型&#xff1a;计划 螺旋模型&#xff1a;风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合&#xff1a;模块内部功能紧密 模块之间依赖程度小 高内聚&#xff1a;指的是一个模块内部的功能应该紧密相关。换句话说&#xff0c;一个模块应当只实现单一的功能…...

编程新知 2026/2/10 0:32:51

VSCode 没有添加Windows右键菜单

关键字&#xff1a;VSCode&#xff1b;Windows右键菜单&#xff1b;注册表。 文章目录 前言一、工程环境二、配置流程1.右键文件打开2.右键文件夹打开3.右键空白处打开文件夹 三、测试总结 前言 安装 VSCode 时没有注意&#xff0c;实际使用的时候发现 VSCode 在 Windows 菜单栏…...

编程新知 2026/2/8 22:07:37

学习 Hooks【Plan - June - Week 2】

一、React API React 提供了丰富的核心 API&#xff0c;用于创建组件、管理状态、处理副作用、优化性能等。本文档总结 React 常用的 API 方法和组件。 1. React 核心 API React.createElement(type, props, …children) 用于创建 React 元素&#xff0c;JSX 会被编译成该函数…...

编程新知 2026/1/5 6:06:59

FTPS、HTTPS、SMTPS以及WebSockets over TLS的概念及其应用场景

一、什么是FTPS&#xff1f; FTPS&#xff0c;英文全称File Transfer Protocol with support for Transport Layer Security (SSL/TLS)&#xff0c;安全文件传输协议&#xff0c;是一种对常用的文件传输协议(FTP)添加传输层安全(TLS)和安全套接层(SSL)加密协议支持的扩展协议。…...

编程新知 2026/2/5 3:53:19