AtCoder Beginner Contest 290 G. Edge Elimination(思维题 枚举+贪心)
题目
T(T<=100)组样例,每次给出一棵深度为d的k叉树,
其中,第i层深的节点个数为
保证k叉树的所有节点个数tot不超过1e18,
求在k叉树上构建一棵大小恰为x的连通块,所需要断开的最少的树边的条数(x<=tot<=1e18)
思路来源
乱搞AC
题解
其实不太知道为什么算个G题,可能是因为F题卡住了太多人
考虑连通块的点的lca位于哪一层,枚举lca所在层为第i层,
如果是第0层,不用切断,如果是第1层到第d层,需要先切断一条边,
只考虑第i层为根的这棵子树,若这棵子树不足x个点,可以直接跳过
否则,当前这棵子树总的点数一定大于x(等于x的情况直接break即可)
计当前还需要删的点的个数为sum2,当前删掉的边数为cur,
子树当前层的点为根及以下层点的总数为now,子树下一层的点为根及以下层的点数为nex
此刻,一定是优先断开靠上的边,靠上的一条边能直接削掉大小为nex的一棵子树
通过下取整确定削几棵,余数在下一层里考虑,直到要删的点为0或考虑到最后一层即可
代码
#include<bits/stdc++.h>
using namespace std;
const int N=65;
typedef long long ll;
int t,c;
ll d,k,x,a[N],sum[N],now,cur;
int main(){cin>>t;while(t--){cin>>d>>k>>x;a[0]=1;sum[0]=1;cur=0;for(int i=1;i<=d;++i){a[i]=1ll*a[i-1]*k;sum[i]=sum[i-1]+a[i];}ll ans=sum[d];for(int i=0;i<=d;++i){ll sum2=sum[i]-x,now=sum[i],cur=(i<d);if(sum2<0)continue;while(sum2>0){ll nex=(now-1)/k;cur+=sum2/nex;//printf("sum:%lld nex:%lld cur:%lld\n",sum,nex,cur);sum2%=nex;now=nex;}ans=min(ans,cur);}cout<<ans<<endl;}return 0;
} 相关文章:
AtCoder Beginner Contest 290 G. Edge Elimination(思维题 枚举+贪心)
题目 T(T<100)组样例,每次给出一棵深度为d的k叉树, 其中,第i层深的节点个数为 保证k叉树的所有节点个数tot不超过1e18, 求在k叉树上构建一棵大小恰为x的连通块,所需要断开的最少的树边的条数(x<tot<1e18)…...
数据挖掘概述
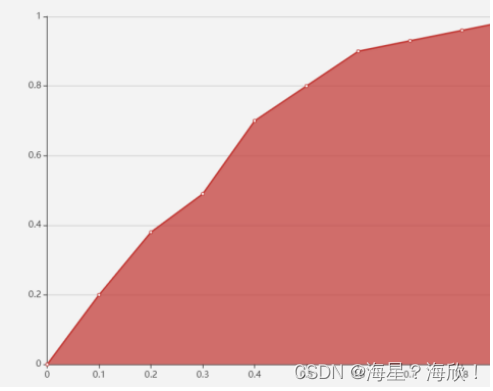
目录1、数据挖掘概述2、数据挖掘常用库3、模型介绍3.1 分类3.2 聚类3.3 回归3.4 关联3.5 模型集成4、模型评估ROC 曲线5、模型应用1、数据挖掘概述 数据挖掘:寻找数据中隐含的知识并用于产生商业价值 数据挖掘产生原因:海量数据、维度众多、问题复杂 数…...

linux kernel iio 架构
linux kernel iio 架构讲解Linux IIO(Industrial I/O)架构是Linux内核提供的一种用于支持各种类型传感器和数据采集设备的子系统,包括温度、压力、湿度、加速度、光度等多种传感器。IIO架构的核心是一个通用的IIO子系统,它提供了一…...

Socket通信详解
Socket通信详解 文章目录Socket通信详解Socket流程介绍函数介绍编程实例Socket流程介绍 socket通信类似于电话通信,其服务器基本流程就是 Created with Raphal 2.3.0安装电话socket()分配电话号码bind()连接电话线listen()拿起话筒accept()函数介绍 socket() 其中…...
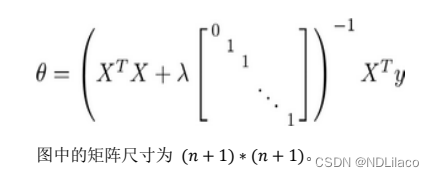
多分类、正则化问题
多分类问题 利用逻辑回归解决多分类问题,假如有一个训练集,有 3 个类别,分别为三角形 𝑦 1,方框𝑦 2,圆圈 𝑦 3。我们下面要做的就是使用一个训练集,将其分成 3 个二…...

史上最全面的软件测试面试题总结(接口、自动化、性能全都有)
目录 思维发散 Linux 测试概念和模型 测试计划与工具 测试用例设计 Web项目 Python基础 算法 逻辑 接口测试 性能测试 总结感谢每一个认真阅读我文章的人!!! 重点:配套学习资料和视频教学 思维发散 一个球ÿ…...

速来~与 Werner Vogels 博士一起探索敏捷性与创新速度一起提升的秘方
Amazon Web Services 的现代应用程序创新一直是 Amazon 公司坚持追求的核心目标。约20年前,我们经历了一次彻底的转型,旨在建立起“发明、发布、再发明、再发布、重新开始、洗牌、再重复”的快速迭代流程。正是此番探索,彻底改变了我们构建应…...

Apache Hadoop、HDFS介绍
目录Hadoop介绍Hadoop集群HDFS分布式文件系统基础文件系统与分布式文件系统HDFS简介HDFS shell命令行HDFS工作流程与机制HDFS集群角色与职责HDFS写数据流程(上传文件)HDFS读数据流程(下载文件)Hadoop介绍 用Java语言实现开源 允许…...
python“r e 模块“常见函数详解
正则表达式:英文Regular Expression,是计算机科学的一个重要概念,她使用一种数学算法来解决计算机程序中的文本检索,匹配等问题,正则表达式语言是一种专门用于字符串处理的语言。在很多语言中都提供了对它的支持,re模块…...

【数据结构】二叉树的四种遍历方式——必做题
写在前面学完上一篇文章的二叉树的遍历之后,来尝试下面的习题吧开始做题144. 二叉树的前序遍历 - 力扣(LeetCode)94. 二叉树的中序遍历 - 力扣(LeetCode)145. 二叉树的后序遍历 - 力扣(LeetCode)…...

Nginx使用“逻辑与”配置origin限制,修复CORS跨域漏洞
目录1.漏洞报告2.漏洞复现3.Nginx 修复3.1 添加请求头3.2 配置origin限制2.3 调整origin限制1.漏洞报告 漏洞名称: CORS 跨域漏洞等级: 中危漏洞证明: Origin从任何域名都可成功访问,未做任何限制。漏洞危害: 因为同源…...
Laravel框架02:路由与控制器
Laravel框架02:路由与控制器一、路由配置文件二、路由参数三、路由别名四、路由群组五、控制器概述六、控制器路由七、接收用户输入一、路由配置文件 以web网页路由文件为例: 默认根路由 路由定义格式Route::请求方式(请求的URL, 匿名函数或控制响应的方…...
)
【POJ 2418】Hardwood Species 题解(映射)
描述 阔叶树是一种植物群,具有宽阔的叶子,结出果实或坚果,通常在冬天休眠。 美国的温带气候造就了数百种阔叶树种的森林,这些树种具有某些生物特征。例如,虽然橡树、枫树和樱桃都是硬木树,但它们是不同的物…...
)
React组件之间的通信方式总结(下)
一、写一个时钟 用 react 写一个每秒都可以更新一次的时钟 import React from react import ReactDOM from react-domfunction tick() {let ele <h1>{ new Date().toLocaleTimeString() }</h1>// Objects are not valid as a React child (found: Sun Aug 04 20…...
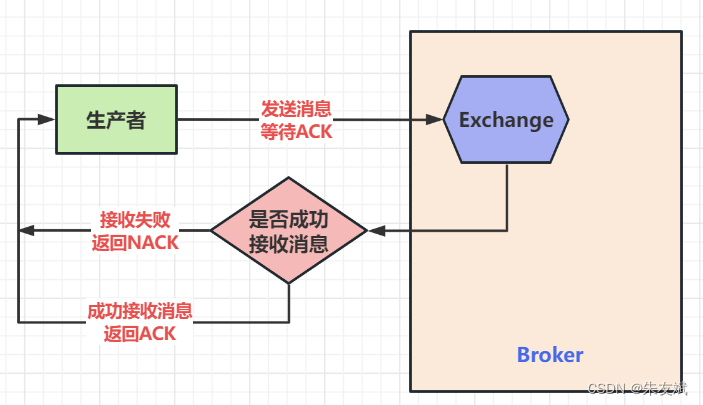
【RabbitMQ笔记07】消息队列RabbitMQ七种模式之Publisher Confirms发布确认模式
这篇文章,主要接收消息队列RabbitMQ七种模式之Publisher Confirms发布确认模式。 目录 一、消息队列 1.1、发布确认模式 1.2、案例代码 (1)引入依赖 (2)编写生产者【消息确认--单条确认】 (3…...

【华为OD机试模拟题】用 C++ 实现 - IPv4 地址转换成整数(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 去重求和(2023.Q1) 文章目录 最近更新的博客使用说明IPv4 地址转换成整数题目输入输出示例一输入输出说明示例一输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,...

闭包与高阶函数
文中内容均来自于曾探《JavaScript设计模式与开发实践》的学习笔记。闭包作用域变量的作用域,就是指变量的有效范围。局部变量、全局变量。变量的搜索是从内到外而非从外到内的。变量的生命周期对于全局变量莱索,全局变量的生命周期是永久的,…...

人工智能轨道交通行业周刊-第35期(2023.2.20-2.26)
本期关键词:重庆智慧轨道、智能运维主机、标准轨距、地方铁路公报、景深、机器视觉应用 1 整理涉及公众号名单 1.1 行业类 RT轨道交通人民铁道世界轨道交通资讯网铁路信号技术交流北京铁路轨道交通网上榜铁路视点ITS World轨道交通联盟VSTR铁路与城市轨道交通Rai…...

快慢指针判断链表是否有环
快慢指针判断链表是否有环 单链表有可能存在环,有些情况下要判断一个单链表是否有环。数组的有个快慢指针的方法,其实单链表和数组有相似的地方,可以使用快慢指针的方法。具体做法如下: 首先创建两个指针,它们初始时…...

《MongoDB入门教程》第26篇 聚合统计之$max/$min表达式
本文将会介绍两个 MongoDB 表达式,返回一组数据中最大值的 $max 表达式,以及返回一组数据中最小值的 $min 表达式。 $max 表达式 $max 表达式用于返回一组数据中的最大值,语法如下: { $max: <expression> }$max 表达式在…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
