常用排序算法的理解
1.插入排序
插入排序的思想是将一个记录插入到已经排好序的有序表中,从而形成一个新的、记录数加1的有序表。在其实现过程使用双层循环,外层循环是进行插入的次数(也可以理解为比较的轮数),内层循环是当前记录查找插入有序表的位置,并进行移动(可以理解为每一轮可能会比较的次数)
排序过程示例:1,7,3,2,9
①1,7,3,2,9 //插入7,7>1所以不需要交换
②1,3,7,2,9 //插入3,3<7需要交换,3>1不需要交换
③1,2,3,7,9 //插入2,2<7交换,2<3交换,2>1不交换
④1,2,3,7,9 //插入9,9>7不交换,9>3不交换,9>2不交换,9>1不交换
int[] a = {1, 7, 3, 2, 9, 10, 5};int N = a.length;for (int i = 1; i < N; i++) {int temp = a[i];int j ;for (j = i; j > 0 && temp < a[j - 1]; j--) {a[j] = a[j-1];}a[j] = temp;}
note
插入排序是一种比较简单的排序算法,它的空间复杂度是O(1),时间复杂度则需要分情况,如果记录基本有序的情况下,例如:
1,2,3,4,5,6,7,8
这种情况下的时间复杂度最小,因为第n个均大于第n-1个,不会进入第二层for循环,所以总比较次数为O(n-1),近似为O(n)。反之,如果是下面这种情况:
8,7,6,5,4,3,2,1
则每轮循环都需要比较n-1次,所以总比较次数为O((n-1)*n/2)。由于记录的不确定性,所以直接插入排序的平均时间复杂度定为O(n*n)。但是我们可以利用记录数比较少或者基本有序的情况下插入排序性能最好这个特点
①希尔排序:排序过程是先将记录分成几个大区间执行插入排序,再将区间分成更小的区间执行插入排序,直到最后区间间隔为1(说明是相邻记录之间比较)执行最后的插入排序。先将记录分为大区间排序后,会让记录形成基本有序的样子,这样缩小区间后再执行插入排序比较次数就会变少,总的时间复杂度要小于O(nn)*。有关希尔排序详细的内容可以看下这篇文章图解排序算法(二)之希尔排序
排序过程示例:1, 4, 9, 3, 2, 7, 0, 6
定义最开始间隔是4(length/2),所以第一轮比较的数是相隔长度为4的记录之间的比较,比较的记录分别是(1,2), (4,7), (9,0),(3,6)
①1, 4, 0, 3, 2, 7, 9, 6 //1<2不交换,4>7不交换,9>0交换,3<6不交换
接着第二轮间隔是2(4/2),所以这轮是相隔2位记录之间的比较,比较的记录分别是(1,0,2,9), (4,3,7,6)
②0, 3, 1, 4, 2, 6, 9, 7 //(1,0,2,9)(4,3,7,6)执行直接插入排序
接着第三轮间隔是1(2/2),这时排序过程已经完全变成了直接插入排序。所以此轮的比较是所有记录
③0, 1, 2, 3, 4, 6, 7, 9
int[] arr = {1, 4, 7, 3, 2, 9, 0, 13, 6, 3, 2, 5, 6, 5, 7, 1, 2, 0};int d = arr.length / 2;
while (d >= 1) {shell_insert(arr, arr.length, d);d /= 2;
}private static void shell_insert(int arr[], int size, int d) {for (int i = d; i < size; i++) {int j = i - d;int key = arr[i];while (j >= 0 && arr[j] > key) {arr[j + d] = arr[j];j -= d;}if (j != i - d)arr[j + d] = key;}
}
②二分插入排序:插入排序最坏的情况是一个记录需要与前面的所有记录比较,但是前面的记录已经是有序的了,如果挨个比较效率就太慢了,所以可以使用二分查找的方式比较数据,这样可以减少比较次数,基本达到O(nlog2N)的效果,但是需要注意的是记录的移动次数并没有改变。
1,2,3,4,5,6,7,8,0
例如上面的一行记录,前面的八个记录数已经排好序。待排序0时,如果使用直接插入排序,需要比较8次,移动8次;如果使用二分插入排序,只需要比较3次,移动8次。时间上要比直接插入快些。
int[] arr = {1, 4, 7, 3, 2, 9, 0, 13, 6, 3, 2, 5};int N = arr.length;
for(int i=1;i<N;i++) {int left = 0, right = i - 1, temp = arr[i];while (left <= right) {int mid = (left + right) / 2;if (arr[mid] > temp) right = mid - 1;else left = mid + 1;}for (int j = i - 1; j >= left; j--) {arr[j + 1] = arr[j];}arr[left] = temp;
}
2.冒泡排序
冒泡排序是交换排序的一种,排序过程:依次将记录中相邻两个元素比较,如果后者小于前者则交换这两个元素,否则继续前进。一轮循环下来,就像挤泡泡一样将最大的数挤到最后。接着重复执行这个过程,就可以将第二大的数,第三大的数…第n大的数挤到倒数第二位,倒数第三位…倒数第n位。
排序过程示例:1,7,3,2,9
①1, 7, 3, 2, 9 //指针指向1,1<7不交换,指针前进
②1, 3, 7, 2, 9 //指针指向7,7>3交换,指针前进
③1, 3, 2, 7, 9 //指针指向7,7>2交换,指针前进
④1, 3, 2, 7, 9 //指针指向7,7<9不交换,第一轮执行结束,最大值9被挤出。可以看出指针前进的过程中指向的永远是最大值
按照上面的过程循环执行多次,可将7,3,2,1挤到倒数第二,三,四,五位。
int[] arr = {1, 4, 7, 3, 2, 9, 0, 13, 6, 3, 2, 5, 6};
int size = arr.length;for (int i = 0; i < size - 1; ++i) {for (int j = 0; j < size - 1 - i; ++j) {if (arr[j] > arr[j + 1]) {swap(arr, j, j + 1);}}
}
note:
冒泡排序的比较次数永远都是O(n*n),没有最好最坏的情况,移动次数可能会由于最好情况(记录有序)而为0。所以冒泡排序的平均时间复杂度也是O(n*n),而且它和直接插入排序一样,是一种稳定的排序算法。
冒泡排序之所以慢,是因为要执行n-1轮循环,每轮循环都要比较n-i-1个数,所以如果能减少比较的轮数或者每轮比较的次数,就可以提高算法的效率。
3.快速排序
减少每轮比较次数的算法,这是一种目前认为比较快的算法。快速排序每轮都会确定一个基准值,然后每轮都将大于基准值的排到它右边,小于基准值的排到它左边,这样就确定了基准值的位置。接下来再将基准值左右两边重复执行排序直至完成。
排序过程示例:4, 7, 3, 2, 9, 0 //以首记录为基准,使用左右指针法
①0, 7, 3, 2, 9, 4 //low为左指针指向4会向后移动,high为右指针指向0会向前移动,基准值key=4,首先右指针先移动,high=0<4,low,high交换
②0, 4, 3, 2, 9, 7 //接着左指针移动low=0<4不交换,low=7>4交换
③0, 2, 3, 4, 9, 7 //右指针接着移动high=7>4不交换,high=9>4不交换,high=2<4交换
④0, 2, 3, 4, 9, 7 //左指针接着移动low=2<4不交换,low=3<4不交换,low==high本轮循环结束。
第一轮循环结束后会形成以key=4为分界线的左右两边,左边均小于4,右边均大于4,相当于4排好了位置,接着再对左右两边分别执行快速排序。因为左右两边都不需要再和另外一边的记录数比较这样相当于减少了一半的比较量,所以平均时间复杂度为O(nlog2N)
当然快速排序也有最坏的情况例如:1,2,3,4,5,6,7,8 选择1为基准值时,第一轮排序完成时,记录全在1的右边,导致下一轮的比较并没有减少记录量,这时时间复杂度又回到了O(n*n)。
private static int partition(int[] a, int low, int high){int key = a[low];while( low < high ){while(low < high && a[high] >= key) high--;a[low] = a[high];while(low < high && a[low] <= key) low++;a[high] = a[low];}a[low] = key;return low;
}private static void quick_sort(int[] a, int low, int high){if(low >= high) return;int keypos = partition(a, low, high);quick_sort(a, low, keypos-1);quick_sort(a, keypos+1, high);
}
4.选择排序
选择排序和冒泡排序有些相似,但是选择排序并不是比较相邻两个记录的大小,而是假设第一个记录为基准值(最大值或者最小值),然后依次与后面的值比较,如果后面的值小于(大于)这个基准值,则用变量记录这个较小值(较大值)的下标。然后用这个变量所对应的较小值接着和后面的值比较,最后得到最小值的下标,然后让变量所对应的最小值与基准值交换。最后最小值(最大值)就会被选到最前面。
排序过程示例:4, 7, 3, 2, 9 //假设4是本轮基准值,让它依次与后面每个值比较,最小值变量的下标用min表示
①4, 7, 3, 2, 9 //4<7,min=0
②4, 7, 3, 2, 9 //4>3,min=2,基准值变成了3
③4, 7, 3, 2, 9 //3>2,min=3,基准值变成了2
④4, 7, 3, 2, 9 //2<9,min=3,本轮结束基准值变成了2,让它与最初的基准值交换位置,这样最小值就选出来了
下一轮从第二个位置开始比较,然后接着循环比较出第三,第四,第五小值。
for (int i = 0; i < size - 1; ++i) {int min = i;for (int j = i; j < size; ++j) {if (a[j] < a[min]) min = j;}if (min != i) {int temp = a[i];a[i] = a[min];a[min] = temp;}
}
note:
选择排序与冒泡排序比较类似,每轮几乎都要与所有元素比较,且只能选出一个最大值(或者最小值),这样无论记录序列是怎样的都需要进行n*n次的比较。
5.堆排序
如果利用数据结构中大根堆(或者小根堆)的特性,父节点永远大于(或者小于)子节点;这样不仅可以选出最大值(最小值),而且次大值(次小值)也一定在根节点的两个子结点中,这样下次只要比较两个子节点就可以选出新的最大值(最小值)。详细的步骤可以查看 图解排序算法(三)之堆排序
排序过程示例:4, 7, 3, 2, 9 //根节点从下标0开始,然后初始建堆。
①4, 7, 3, 2, 9, 0 //首先根据记录构造完全二叉树(大根堆),图中流程①所示
②4, 7, 3, 2, 9, 0 //首先从最后一个非叶子节点开始,先比较它的左右子节点,然后将最大值与父节点比较,如果大于父节点就交换,图中流程②所示
③4, 7, 3, 2, 9, 0 //依次向前一个非叶子节点移动,重复步骤②的过程,直至到达根节点,图中流程③④所示
④9, 4, 3, 2, 7, 0 //如果父节点的其中一个子节点与父节点交换,还需要观察交换后的父节点是否符合大根堆的特性,如果不符合,还需要重新建堆。图中流程④⑤所示
⑤9, 7, 3, 2, 4, 0 //大根堆构建完成(最大值已经找出),这时将堆顶元素与最后一个元素交换,图中流程⑥所示
⑥0, 2, 3, 4, 7, 9 //这时又不是大根堆了,需要重新开始构建大根堆(最后一个元素除外,因为它是已经找出的最值元素,不再参与接下来的过程)得到次大值,接着与倒数第二个元素交换,并重复步骤②③④⑤,得到最终的结果,图中流程⑦至结尾

//此处第一个元素是以下标0开始,结点下标为i,左孩子则为2*i+1,右孩子下标则为2*i+2
private static void heapAdjust(int a[], int s, int m){int key = a[s];for(int j = 2*s + 1; j <= m; j = 2*j + 1 ){if(j+1 < m && a[j] <= a[j+1] ) ++j;if( a[j] <= key ) break;a[s] = a[j];s = j;}a[s] = key;
}
private static void heap_sort(int a[], int size){//初始建堆,从最后一个非叶子节点开始for(int i = size/2-1; i >= 0; --i){heapAdjust(a, i, size-1);}//取堆顶,并且调整for(int i = size-1; i > 0 ; --i){swap(a, 0, i);heapAdjust(a, 0, i-1);}
}
堆排序的过程分为初始建堆,选出根节点并与最后一个记录交换,重新建堆,重新选出根节点并与倒数第n个记录交换。堆排序的优势在于每次选出最大值并交换后,次大值肯定在两个子结点中,接着将次大值交换到根节点,然后只需要对其中一个子节点做重建堆即可。堆排序的时间复杂度可以近似为O(nlog2N)+初始建堆的时间,堆排序使用的是完全二叉树,所以没有最好和最坏情况,每次循环都需要与剩余的一半记录作比较(初始建堆除外)
6.计数排序
计数排序是一种不用比较的排序。计数排序利用的是桶的思想,将不同的数据分到不同的桶中,相同的数据分到同一个桶中并计数,然后反向回收数据,详细过程请查看计数排序流程,排序过程:
①先计算最大和最小值的差值,并创建一个长度是差值加1且用于统计记录出现次数的辅助数组,将记录按照辅助数组的下标值统计。
②将统计得到的数组按顺序依次取出,即为排序成功。
private static void countingSort(int[] arr) {int maxValue = arr[0];int minValue = arr[0];for (int value : arr) {if (maxValue < value) {maxValue = value;} else if (minValue > value) {minValue = value;}}int[] bucket = new int[maxValue - minValue + 1];for (int value : arr) {bucket[value - minValue]++;}int index = 0;for (int j = 0; j < bucket.length; j++) {while (bucket[j] > 0) {arr[index++] = j;bucket[j]--;}}
}
note:
计数排序虽然简单,但是需要利用的辅助数组(桶)可能会随着数据差值的变大而变大。例如如果排序序列是65535, 256, 0, 1,就需要创造大小为65536的数组,即便参与排序的只有四个。
基数排序
同样利用计数排序的桶思想,但是不再按照差值的长度新建辅助数组,而是利用数字范围分配到对应的桶中。例如对数字进行排序,则新建一个[0,9]的辅助数组,依次将记录的关键字(个位数字或者十位数字)分配至桶中,是一种重复进行分配-收集-分配-收集的过程。
排序过程示例:21, 34, 54, 13, 76, 24, 45, 51, 78, 23, 15,如下图表格中的每一行代表一个个桶。
①首先分析出所有记录的最大位数,确定分配-收集的次数,这里最大位数是2。
②21, 51, 13, 23, 34, 54, 24, 45, 15, 76, 78 //先对个位数字进行分配回收,如下图中第一个表格和第二个矩形中的内容。
③13, 15, 21, 23, 24, 34, 45, 51, 54, 76, 78 //再对十位数字进行分配回收,由于已经对个位数字按照顺序好了,所以在进行十位数字分配时个位数小的记录会理所当然的放在每个桶的前面。这样再对十位数字回收时就会得到排序好的记录。如下图第二个表格和第三个矩形中的内容。
private static void radixSort(int[] arr, int maxDigit) {int mod = 10;int dev = 1;for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {//先设置辅助数组容量为空,待需要时再调用方法扩容int[][] counter = new int[10][0];for (int j = 0; j < arr.length; j++) {int bucket = ((arr[j] % mod) / dev);counter[bucket] = arrayAppend(counter[bucket], arr[j]);}int pos = 0;for (int[] bucket : counter) {for (int value : bucket) {arr[pos++] = value;}}}
}
//辅助数组自动扩容
private static int[] arrayAppend(int[] arr, int value) {arr = Arrays.copyOf(arr, arr.length + 1);arr[arr.length - 1] = value;return arr;
}

基数排序的平均时间复杂度为O(d(r+n)),因为基数排序是分配与收集的重复过程,所以位数d是循环次数,O(n)是每轮分配的次数,O®可以看成是每轮收集的次数,其中r为关键字的范围,文中是[0, 9],此外r还有可能是八进制或者字符。基数排序适合位数差异比较小且排序记录较多的情况。例如10000个1000以内记录的排序。
不过基数排序使用了空间换时间的方式,因为基数排序使用了辅助数组帮忙,参考的链接中说基数排序的空间复杂度是O(n+rb),这种说法是因为分配的过程中rb个桶,此外收集过程还需要n个大小的数组存储每轮收集的结果。但是还得视程序而定,例如上述程序中收集使用的数组还是初始数组,分配过程则使用自动扩容性质的数组,所以可以认为上述程序的空间复杂度是O(n)。
参考:八大排序算法
基数排序
相关文章:

常用排序算法的理解
1.插入排序 插入排序的思想是将一个记录插入到已经排好序的有序表中,从而形成一个新的、记录数加1的有序表。在其实现过程使用双层循环,外层循环是进行插入的次数(也可以理解为比较的轮数),内层循环是当前记录查找插入…...

Python小程序 - 文件解析
1. 目录下文件解析:特定文件、文件列表、文件数 Windows文件目录分格使用“ / ” 或 “ \\ ”文件目录路径包含空格的,绝对路径使用“双引号”,保证文件路径的可识别性保存和读取结果时,使用 encodingUTF-8可以添加对文件目录的过…...

.mxdown-V-XXXXXXXX勒索病毒的最新威胁:如何恢复您的数据?
导言: 在数字时代,网络安全威胁层出不穷,其中.mxdown-V-XXXXXXXX、.vollhavhelp-V-XXXXXXXX、.arricklu-V-XXXXXXXX勒索病毒已成为备受关注的问题。这种病毒以其高级加密技术和威胁勒索金的方式,严重危害用户和企业的数据安全。本…...

audio 标签动态src 且src是http无法播放问题
<audioref"audio" :src"src"alt"加载失败"controls/>src是动态传参的 无法播放因为动态src需要在赋值后对audio进行重载 this.$refs.audio.load()注意如果,src跟本项目地址IP端口协议不同,会出现跨域问题。audio标…...

Leetcode—485.最大连续1的个数【中等】明天修改
2023每日刷题(十五) Leetcode—2.两数相加 迭代法实现代码 /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/ struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l…...
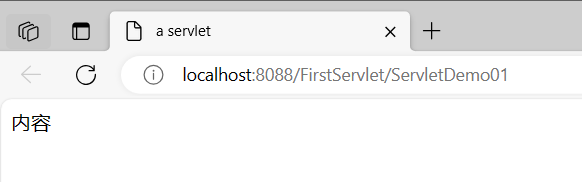
JavaWeb 怎么在servlet向页面输出Html元素?
service()方法里面的方法体: resp.setContentType("text/html;charsetutf-8");//获得输出流PrintWriter对象PrintWriter outresp.getWriter();out.println("<html>");out.println("<head><title>a servlet</title>…...
Spring及SpringBoot中AOP的使用
Spring中AOP示例 <dependencies><!--Spring核心包--><dependency><groupId>org.springframework</groupId><artifactId>spring-core</artifactId><version>5.3.6</version></dependency><!--引入SpringBean--&…...
cmake多目录构建初步成功
目录和代码和 首次cmake 多目录构建失败 此文一样; 只有一个CMakeLists.txt; cmake_minimum_required(VERSION 3.10) project(mytest3 VERSION 1.0) include_directories("${PROJECT_SOURCE_DIR}/include") add_executable(mytest3 src/main…...
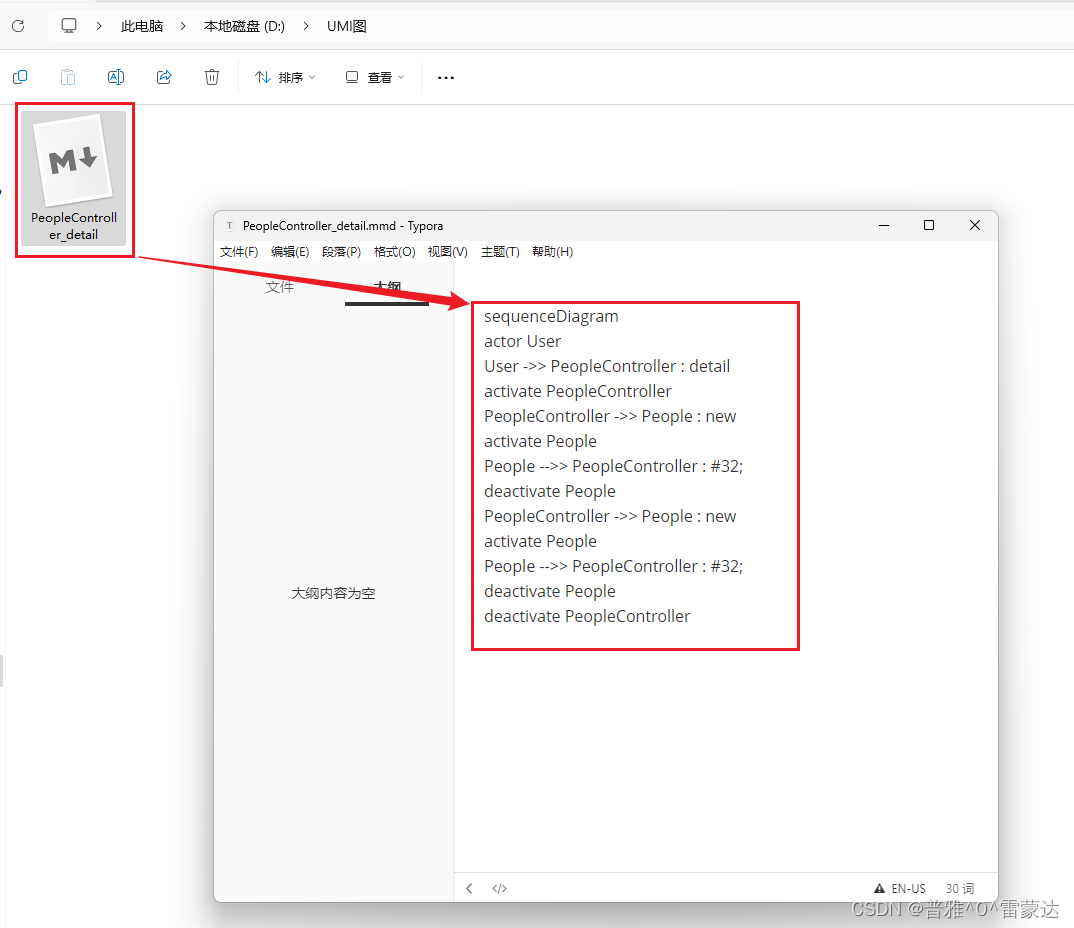
idea插件(一)-- SequenceDiagram(UML自动生成工具)
目录 1. 安装 2. 默认快捷键 3. 操作说明 4. 导出为图片与UML类图 4.1 导出为图片: 4.2 导出 UML 类图 SequenceDiagram是从java、kotlin、scala(Beta)和groovy(limited)代码生成简单序列图(UML&…...

STM32 APP跳转到Bootloader
stm32 app跳转到bootloade 【STM32】串口IAP功能的实现,BootLoader与App相互跳转 STM32 从APP跳入BootLoader问题...

[RISC-V]verilog
小明教IC-1天学会verilog(7)_哔哩哔哩_bilibili task不可综合,function可以综合...
Log4j-tag丢失
一、引言 最近有个线上日志丢失tag的问题,是组内封装了后置请求的拦截器把请求的响应结果存到ClickHouse里面去,但是日志总有一些tag丢失。 作者提出父级线程的threadlocal被清空,同事认为可能是threadlocal的弱引用在gc的时候被回收。两种想…...

代码随想录算法训练营第五十六天|1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和 动态规划
1143. 最长公共子序列 int longestCommonSubsequence(char * text1, char * text2){int len1 strlen(text1);int len2 strlen(text2);int dp[len11][len21];for (int i 0; i < len1; i){for (int j 0; j < len2; j){dp[i][j] 0;}}for (int i 1; i < len1; i){f…...
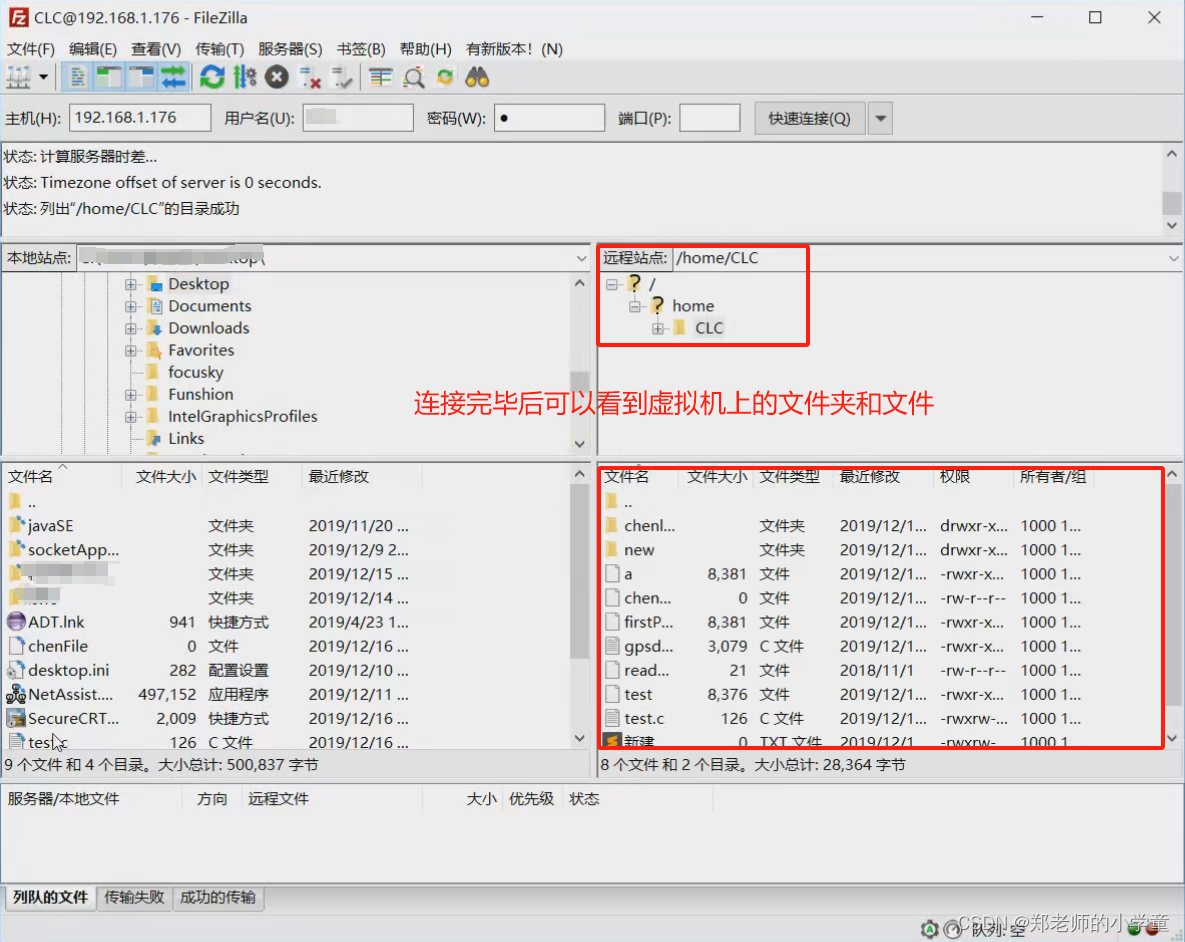
虚拟机和Windows的文件传输
拖拽/复制粘贴 直接将虚拟机linux系统的文件拖曳到windows桌面,或者直接将windows的文件拖曳到虚拟机linux系统当中,可以实现文件传输。当然复制粘贴方式也可以,但是前提是需要下载安装好VMware tools。 共享文件夹 概念:在Win…...
)
leetcode分类刷题:二叉树(八、二叉搜索树特有的自顶向下遍历)
二叉搜索树是一个有序树:每个二叉树都满足左子树上所有节点的值均小于它的根节点的值,右子树上所有节点的值均大于它的根节点的值;利用该性质,可以实现二叉搜索树特有的自顶向下遍历 700. 二叉搜索树中的搜索 思路1、自顶向下的遍…...

Vue 插槽 组件插入不固定内容
定义好一个组件,如果想插入图片或视频这非常不好的控制应该显示什么,这个时候可以使用插槽插入自定义内容 默认插槽 <Login><template><h1>我是插入的内容</h1></template></Login >组件 <slot></slot>…...

webpack打包时配置环境变量
webpack打包时配置环境变量 一、常规环境变量配置1. 使用webpack.DefinePlugin定义全局常量2. 在Vue静态页面中使用该环境变量 二、纯静态文件配置环境变量1. 使用npm或yarn安装html-webpack-plugin2. 在Webpack配置中引入并使用插件3. 使用htmlwebpackplugin.options方式配置环…...
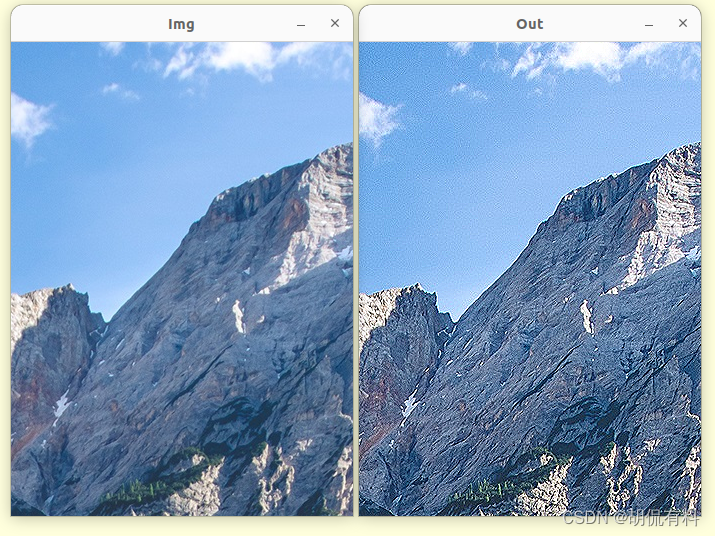
【c++|opencv】一、基础操作---3.访问图像元素
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 访问图像元素 1. 访问图像像素 1.1 访问某像素 //灰度图像: image.at<uchar>(j, i) //j为行数,i为列数 //BGR彩色图像 i…...

机器视觉3D项目评估的基本要素及测量案例分析
目录 一. 检测需求确认 1、产品名称:【了解是什么产品上的零件,功能是什么】 2、*产品尺寸:【最大兼容尺寸】 3、*测量项目:【确认清楚测量点位】 4、*精度要求:【若客户提出的精度值过大或者过小,可以和客…...

力扣日记10.31-【栈与队列篇】前 K 个高频元素
力扣日记:【栈与队列篇】前 K 个高频元素 日期:2023.10.31 参考:代码随想录、力扣 347. 前 K 个高频元素 题目描述 难度:中等 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

使用python进行图像处理—图像变换(6)
图像变换是指改变图像的几何形状或空间位置的操作。常见的几何变换包括平移、旋转、缩放、剪切(shear)以及更复杂的仿射变换和透视变换。这些变换在图像配准、图像校正、创建特效等场景中非常有用。 6.1仿射变换(Affine Transformation) 仿射变换是一种…...

Redis——Cluster配置
目录 分片 一、分片的本质与核心价值 二、分片实现方案对比 三、分片算法详解 1. 范围分片(顺序分片) 2. 哈希分片 3. 虚拟槽分片(Redis Cluster 方案) 四、Redis Cluster 分片实践要点 五、经典问题解析 C…...
