当前位置： 首页 > news >正文

SpringCloud(五) Eureka与Nacos的区别

news 2026/2/10 22:05:10

SpringCloud(二) Eureka注册中心的使用-CSDN博客

SpringCloud(四) Nacos注册中心-CSDN博客

在这两篇博文中我们详细讲解了Eureka和Nacos分别作为微服务的注册中心的使用方法和注意事项,但是两者之间也有一些区别.

一, Nacos实例分类

Nacos实例分为两种类型:

  • 临时实例:如果实例宕机超过一定时间,会从服务列表剔除,默认的类型;
  • 非临时实例:如果实例宕机,不会从服务列表中剔除.

一般默认的实例类型是临时实例,这一点可以在Nacos的控制界面看到:

可以通过配置文件修改一个实例为永久实例:

spring:cloud:nacos:discovery:ephemeral: false # 设置为非临时实例

二, Eureka与Nacos的异同

Nacos和Eureka整体结构类似,服务注册,服务拉取,心跳等待,但是存在一定差异:

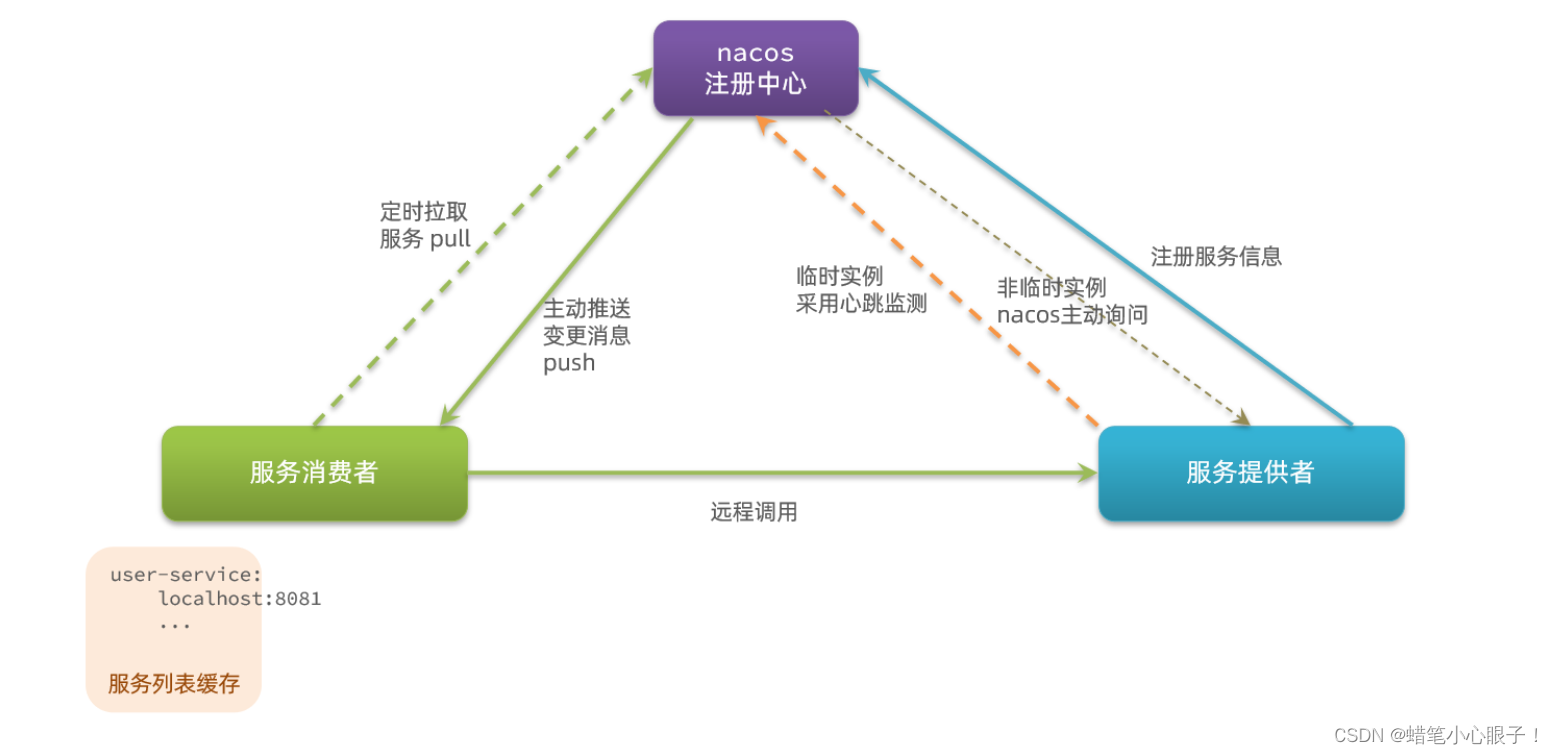
Nacos和Eureka的共同点:

  • 都支持服务注册和服务拉取
  • 都支持服务提供者心跳方式做健康检测 

Nacos和Eureka的区别:

  • Nacos支持服务端主动检测提供者状态:临时实例采用心跳模式,非临时实例采用主动检测模式
  • 临时实例心跳不正常会被剔除,非临时实例则不会被剔除
  • Nacos支持服务列表变更的消息推送模式,服务列表更新更及时
  • Nacos集群默认采用AP方式,当集群中存在非临时实例时,采用CP模式;Eureka采用AP方式

相关文章：

SpringCloud(五) Eureka与Nacos的区别

SpringCloud(二) Eureka注册中心的使用-CSDN博客 SpringCloud(四) Nacos注册中心-CSDN博客 在这两篇博文中我们详细讲解了Eureka和Nacos分别作为微服务的注册中心的使用方法和注意事项,但是两者之间也有一些区别. 一, Nacos实例分类 Nacos实例分为两种类型: 临时实例:如果实例…...

编程日记 2023/11/1 6:41:01

C语言 DAY07:预编译，宏，选择性编译，库（静态库，动态库）

声明与定义分离 声明：将声明单独封装成一个以.h为后缀名的头文件 定义：将定义的变量，函数，数组所在的源文件单独封装成一个.c文件。其实就是在源文件基础上将定义过的所有东西的声明分离出去就是了。 注意：1.声明的…...

编程日记 2023/11/1 6:40:00

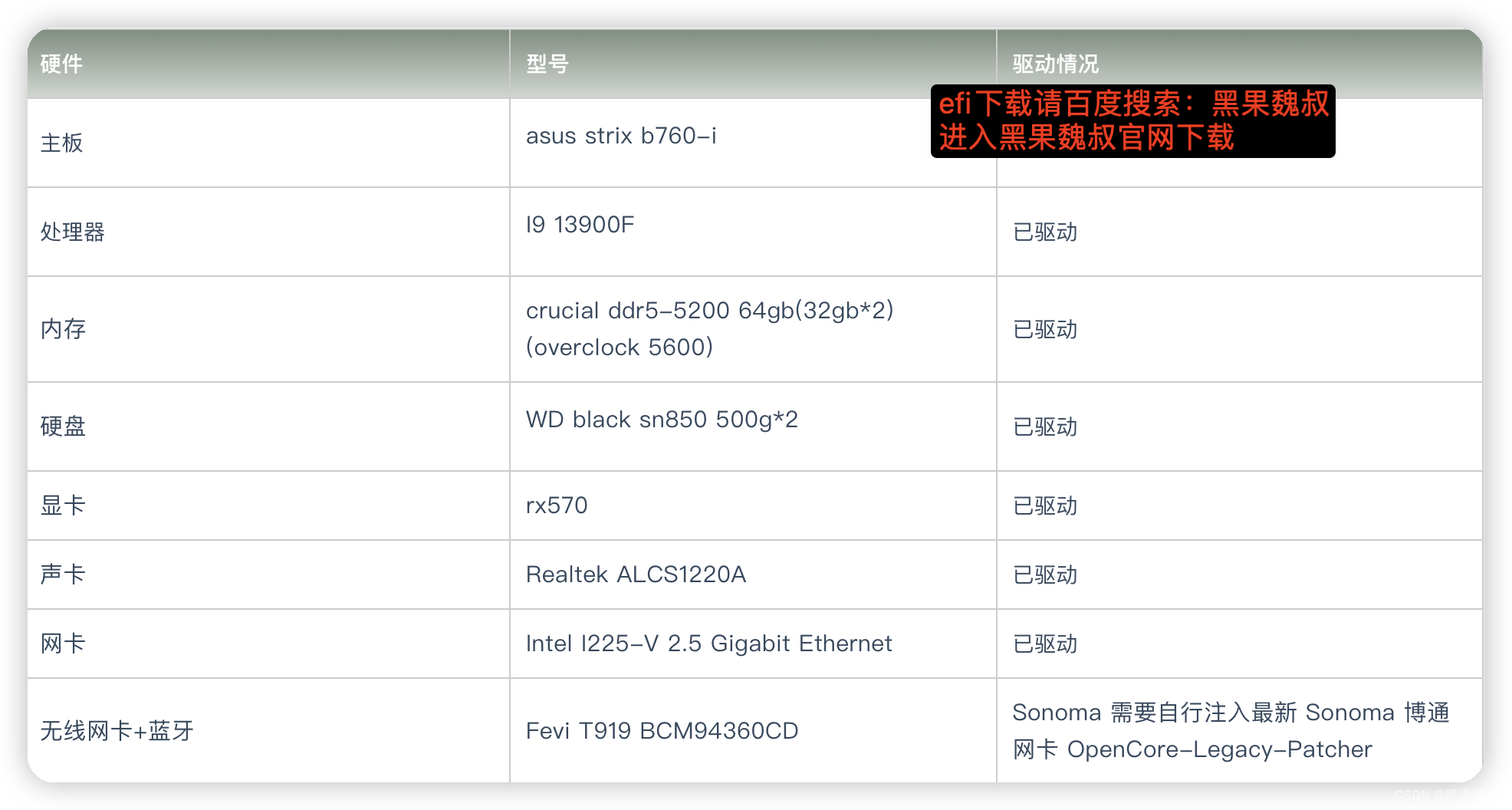
[EFI]asus strix b760-i 13900F电脑 Hackintosh 黑苹果efi引导文件

硬件型号驱动情况主板 asus strix b760-i 处理器 I9 13900F 已驱动内存crucial ddr5-5200 64gb(32gb*2)(overclock 5600)已驱动硬盘 WD black sn850 500g*2 已驱动显卡rx570已驱动声卡Realtek ALCS1220A已驱动网卡Intel I225-V 2.5 Gigabit Ethernet已驱动无线网卡蓝牙Fevi T91…...

编程日记 2023/11/1 6:38:59

力扣383.赎金信

原题链接：383.赎金信 根据题意得出，需要判断第一个字符串内的字符有没有都在第二个字符串内出现(会有重复字符)，并且范围限制在26个英文小写字母 此时可以考虑用一个数组map 作哈希法映射操作 先将遍历第一个字符串，并让每个字符…...

编程日记 2023/11/1 6:37:58

CORS的原理以及在Node.js中的使用

在前端浏览器中的JavaScript代码发起HTTP请求到服务器的Node.js程序，CORS（跨域资源共享）会在以下几个步骤中发挥作用： 前端JavaScript代码发起请求： 前端浏览器中的JavaScript代码使用XMLHttpRequest对象或Fetch API等…...

编程日记 2023/11/1 6:36:57

kotlin实现单例模式

kotlin实现单例模式，大体分为两种方式，一种饿汉式单例模式，一种懒汉式单例模式。 1.饿汉式单例模式 在类前面加上object关键字，就实现了饿汉式单例模式： object singletonDemo { }在kotlin中，使用这种方式…...

编程日记 2023/11/1 6:35:56

【Java】LinkedList 集合

LinkedList集合特点 LinkedList 底层基于双向链表实现增删 效率非常高，查询效率非常低。 LinkedList源码解读分析 LinkedList 是双向链表实现的 ListLinkedList 是非线程安全的（线程是不安全的）LinkedList 元素允许为null,允许重复元素Linked…...

编程日记 2023/11/1 6:34:55

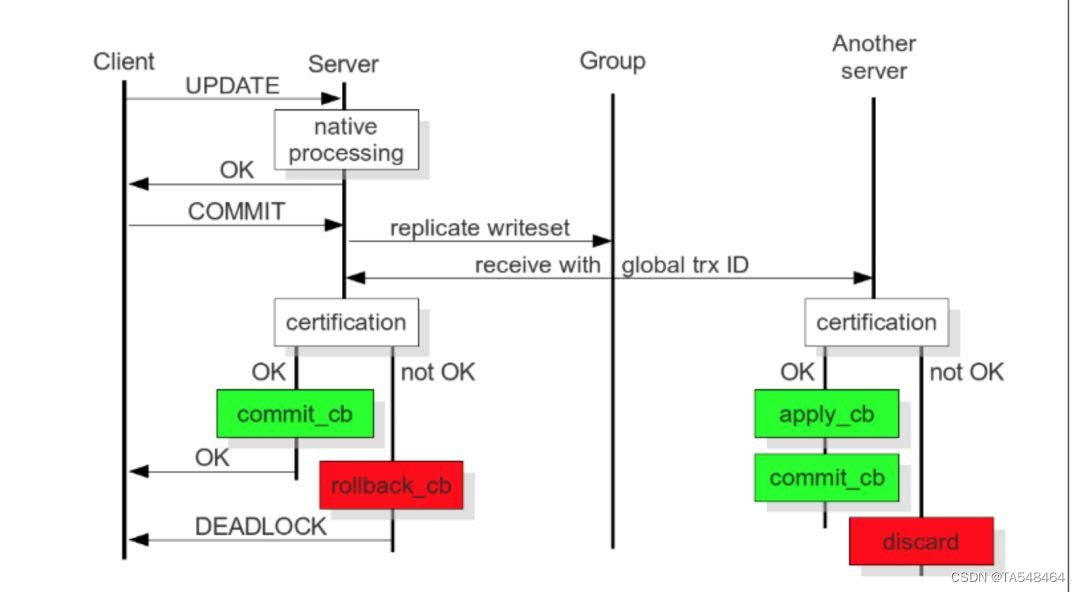
MySQL-Galera-Cluster集群详细介绍

目录 一、什么是Mysql集群？1.单节点mysql存在的常见问题2.mysql集群介绍3.Mysql集群的优点和风险 二、Mysql集群的一些疑问1.mysql的AB复制和Galera Cluster有什么区别？2.什么情况下适用AB复制，什么情况下使用Galera cluster？3.可…...

编程日记 2023/11/1 6:33:53

JavaScript从入门到精通系列第二十六篇：详解JavaScript中的Math对象

大神链接：作者有幸结识技术大神孙哥为好友，获益匪浅。现在把孙哥视频分享给大家。 孙哥连接：孙哥个人主页 作者简介：一个颜值99分，只比孙哥差一点的程序员 本专栏简介：话不多说，让我们一起干翻J…...

编程日记 2023/11/1 6:32:52

u盘直接拔出文件丢失怎么找回？u盘文件恢复办法分享！

u盘作为一种便捷的数据存储设备，被广泛地使用。通过u盘，我们可以在不同设备之间轻松传输文件，然而有时候，我们可能因为匆忙或疏忽并未安全弹出u盘，而是直接将u盘拔出，进而导致重要文件丢失，u盘直…...

编程日记 2023/11/1 6:31:51

rust学习-LinkedList

介绍 A doubly-linked list with owned nodes. 自有节点的双向链表 pub struct LinkedList<T, A = Global> whereA: Allocator, {/* private fields */ }使用 Vec 或 VecDeque 几乎总是更好，因为基于数组的容器通常更快、内存效率更高，并且可以更好地利用 CPU 缓存 …...

编程日记 2023/11/1 6:30:50

搭上直播快车，文旅迎来了更大爆发期？

“直播累计观看人数1083万人次&#xff0c;同期在线峰值10万人&#xff0c;抖音平台销售额800万元&#xff0c;荣登食遍天下榜第一名”。 10月28日&#xff0c;“东方甄选看世界”无锡专场直播落幕&#xff0c;又创造了新成绩&#xff0c;“文旅直播”这一新带货模式的发展可行…...

编程日记 2023/11/1 6:29:48

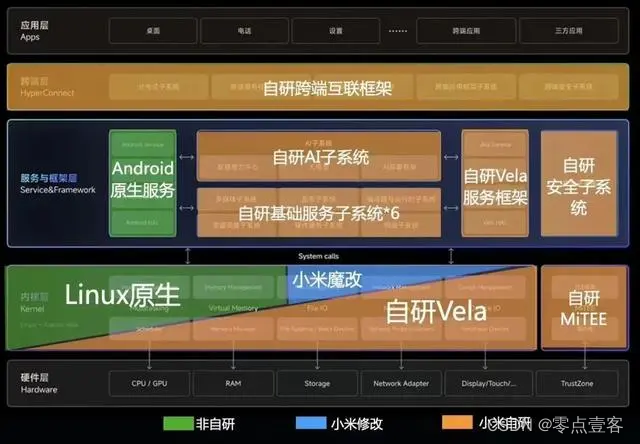
【智能座舱系列】- 深度解密小米Hyper OS,华为HarmonyOS区别

上一篇文章《小米的澎湃OS到底牛不牛？与鸿蒙系统之间差距有多大》，从多个方面比较了小米Hyper OS 与 华为HarmonyOS的区别，本篇文章继续从架构层面深度解读两者本质的区别。 小米澎湃OS是“以人为中心，打造人车家全生态操作系统”，该系统基于深度进化的Android以及自研的V…...

编程日记 2023/11/1 6:28:47

kafka-consumer-groups.sh

通过 kafka-consumer-groups.sh 脚本查看或变更消费组的信息。 查看消费者组信息 ./kafka-consumer-groups.sh --bootstrap-server localhost:9092 --list 查看指定消费者组的消费位移 ./kafka-consumer-groups.sh --bootstrap-server localhost:9092 --describe --group g…...

编程日记 2023/11/1 6:26:45

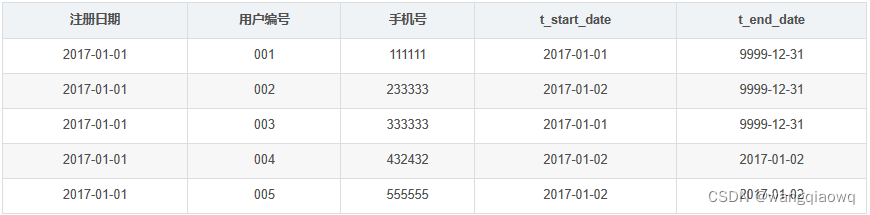
数据仓库-拉链表

在数据仓库中制作拉链表&#xff0c;可以按照以下步骤进行&#xff1a; 确定需求&#xff1a;首先明确需要使用拉链表的场景和需求。例如&#xff0c;可能需要记录历史数据的变化&#xff0c;以便进行时间序列分析等。设计表结构&#xff1a;在数据仓库中&#xff0c;拉链表通…...

编程日记 2023/11/1 6:25:44

【Docker】一些可以直接用的Docker环境

这里罗列一些打包的镜像&#xff0c;方便直接使用。 cu11.6ubuntu18.04 docker push kevinchina/deeplearning:cu11.6ubuntu18.04 FROM nvidia/cuda:11.6.2-cudnn8-devel-ubuntu18.04 RUN apt-get update && apt-get install -y wget git vim curl RUN wget http://…...

编程日记 2023/11/1 6:23:42

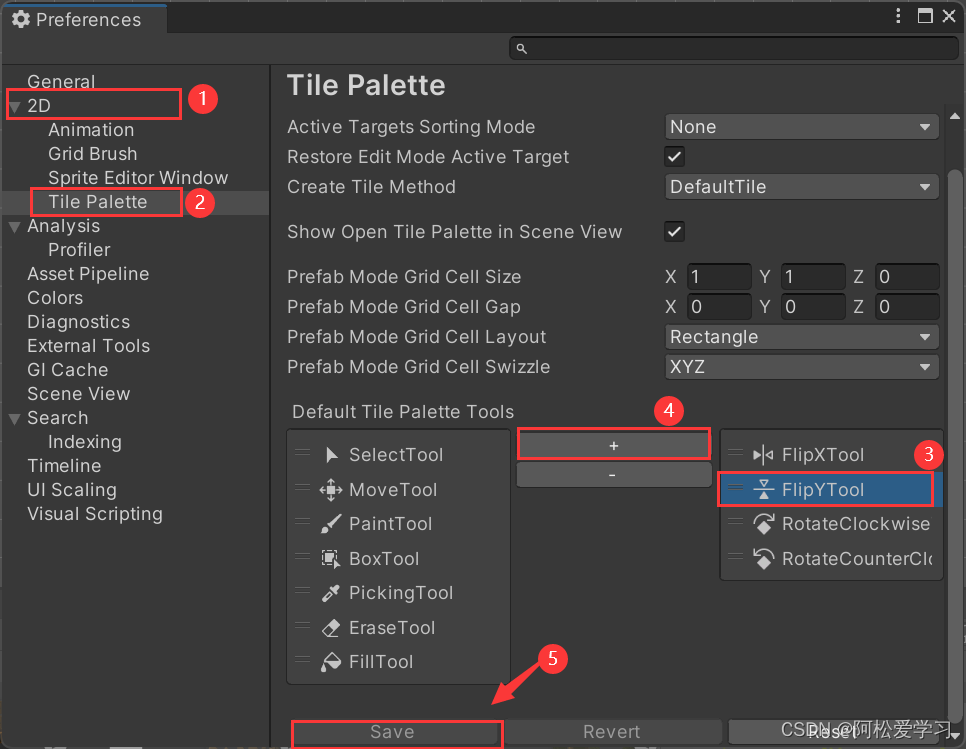
Unity2D中瓦片地图的创建与绘制教程

Unity2D中瓦片地图的创建与绘制 素材切割创建地图创建瓦片绘制地图瓦片调色板画笔拓展素材资源链接 素材切割 选中以下素材&#xff0c;以Tiles为例&#xff08;素材链接在文章最下方&#xff09; 修改素材属性。 将Sprite Mode属性改为Multiple多张&#xff08;不然切割不了&…...

编程日记 2023/11/1 6:22:41

现代的简洁，诠释轻奢的精致！福州中宅装饰，福州装修

轻奢风是一种生活新时尚 优雅、低调、舒适、简单&#xff0c;不断地推陈出新 站在时尚的前沿&#xff0c;引领潮流 中宅装饰集团轻奢风格产品 追求高品质生活细节 以设计精致的空间构造营造出 一种优雅、时尚生活氛围 将低调奢华之美注入现代家居设计中 客厅|The Sitt…...

编程日记 2023/11/1 6:21:40

运用ChatGPT辅助新手学习躺赢者PRO飞控二次开发示例（2023年10月28日）

运用ChatGPT辅助新手学习躺赢者PRO飞控二次开发示例&#xff08;2023年10月28日&#xff09; 1、以飞控预设的飞行任务demo中void flight_subtask_1(void)代码为例分析一下变量flight_subtask_cnt的作用&#xff1f; //逆时针转动90度&#xff0c;完成后降落 void flight_sub…...

编程日记 2023/11/1 6:20:39

【Java】HashCode方法重写注意事项

HashCode方法 HashCode方法是属于Object父类提供的方法&#xff0c;HashCode方法返回该对象的哈希码值。支持该方法是为哈希表提供一些优点&#xff0c;例如&#xff0c;java.util.Hashtable提供的哈希表HashCode的常规协定是&#xff1a;在Java应用程序执行期间&#xff0c;在…...

编程日记 2023/11/1 6:19:38

MySQL 隔离级别：脏读、幻读及不可重复读的原理与示例

一、MySQL 隔离级别 MySQL 提供了四种隔离级别，用于控制事务之间的并发访问以及数据的可见性，不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式，具体如下： 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交（READ UNCOMMITTED）允许出现允许…...

编程新知 2025/9/16 21:01:58

无法与IP建立连接，未能下载VSCode服务器

如题&#xff0c;在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈&#xff0c;发现是VSCode版本自动更新惹的祸&#xff01;&#xff01;&#xff01; 在VSCode的帮助->关于这里发现前几天VSCode自动更新了&#xff0c;我的版本号变成了1.100.3 才导致了远程连接出…...

编程新知 2026/1/22 21:24:01

YSYX学习记录（八）

C语言&#xff0c;练习0&#xff1a; 先创建一个文件夹&#xff0c;我用的是物理机&#xff1a; 安装build-essential 练习1&#xff1a; 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件&#xff0c;随机修改或删除一部分&#xff0c;之后…...

编程新知 2026/1/24 14:31:01

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具

文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

编程新知 2026/2/7 10:59:19

页面渲染流程与性能优化

页面渲染流程与性能优化详解&#xff08;完整版&#xff09; 一、现代浏览器渲染流程&#xff08;详细说明&#xff09; 1. 构建DOM树 浏览器接收到HTML文档后&#xff0c;会逐步解析并构建DOM&#xff08;Document Object Model&#xff09;树。具体过程如下&#xff1a; (…...

编程新知 2026/1/31 11:58:35

Keil 中设置 STM32 Flash 和 RAM 地址详解

文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面（Target 选项卡）1. IROM1（用于配置 Flash）2. IRAM1（用于配置 RAM）二、链接器设置界面（Linker 选项卡）1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数（如果没有勾选上面…...

编程新知 2026/2/7 0:28:16

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现，论文初版实现

摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序&#xff0c;以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务&#xff0c;提供稳定高效的数据处理与业务逻辑支持&#xff1b;利用 uniapp 实现跨平台前…...

编程新知 2026/1/31 10:55:22

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/10/13 2:26:14

在WSL2的Ubuntu镜像中安装Docker

Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包&#xff1a; for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

编程新知 2026/2/4 16:23:56

Spring AI与Spring Modulith核心技术解析

Spring AI核心架构解析 Spring AI&#xff08;https://spring.io/projects/spring-ai&#xff09;作为Spring生态中的AI集成框架&#xff0c;其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似&#xff0c;但特别为多语…...

编程新知 2025/12/14 17:38:21