算法设计与分析期末考试复习(四)
贪心算法(Greedy Algorithm)
找零钱问题
假设有4种硬币,面值分别为:二角五分、一角、五分和一分,现在要找给顾客六角三分钱,如何找使得给出的硬币个数最少?
首先选出1个面值不超过六角三分的最大硬币,即两角五分
然后从六角三分中减去两角五分,剩下三角八分
再选出1个面值不超过三角八分的最大硬币
即又一个两角五分。如此一直做下去……
这里用到的方法就是贪心算法
在这个例子中,找硬币算法得到的结果是整体最优解,问题本身具有最优子结构性质,可以用动态规划算法求解,用贪心算法更简单、更直接、且解题效率更高分。
贪心算法的基本思想
- 贪心算法在每一步选择中都采取在当前状态下最优的选择:目的是希望由此导出的结果是最优的。
- 贪心算法在求解问题时并不着眼于整体最优,它所做出的选择仅仅是当前看来最优的。
- 最优子结构性质:局部最优解能决定全局最优解。
- 问题能够分成子问题来解决。
- 子问题的最优解能递推到最终问题的最优解。
贪心算法与动态规划的区别
动态规划
- 每一步的最优解是由上一步的局部最优解进行选择得到的。
- 因此需要保存(之前求解的)所有子问题的最优解备查。
贪心算法
- 下一步的最优解是由上一步的最优解推导得到的。
- 当前最优解包含上一步最优解,之前的最优解不作保留。
- 在贪心算法中做出的每步决策都无法改变(不能回退)。
二者关系
- 贪心算法本质上是一种更快的动态规划算法。
- 贪心法正确的条件:每一步的最优解一定包含上一步的最优解。
- 如果可以证明:在递归求解的每一步,按贪心选择策略选出的局部最优解,最终可导致全局最优解,则二者是等价的。
**贪心算法对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前结果进行选择,有回退功能。对某些问题动态规划算法并不是最简便的方法,因为有时候确实没有必要知道所有子问题的解。
**
贪心算法得到的结果不能保证全局最优
活动安排问题
设:有n个活动的集合E={1,2,…,n},其中:每个活动都要求竞争使用同一资源(如演讲会场等),而在同一时间内只有一个活动能使用这一资源,每个活动 i 都有一个请求使用该资源的起始时间 si ,每个活动 i 都有一个使用资源的结束时间 fi,且 si < fi ,如果选择了活动 i,则它在半开时间区间[si, fi)内占用资源,若区间[si, fi)与[sj, fj)不相交,则称活动i与活动j是相容的,也就是说,当 si ≥ fj 或 sj≥fi 时,活动i与活动j相容。
活动安排问题就是要在所给的活动集合中,选择最大的相容活动子集合,使尽可能多的活动能使用资源。
证明:按F[1:n]递增顺序进行贪心选择可得到全局最优解
首先证明活动安排问题有一个最优解以贪心选择开始
- 设E={1,…,n}为给定活动集合(按结束时间非减序排列),显然活动1具有最早的完成时间。
- 设集合A是该问题的一个最优解,同时第一个活动是活动k。
- 若k=1,则A就是一个以贪心选择开始的最优解。
- 若k>1,则设(A-{k})∪{1},由于由于F[1]≤F[k],且A中活动相容,故B中活动也相容,由于B和A中包含的活动个数相同,故B也是最优的。
得证:总存在一个以贪心选择开始的最优活动安排方案。
用数学归纳法证明贪心算法的解是全局最优解
- 设E={1,2,…,n}为所给的活动集合,在做了贪心选择,即选择了活动1后,原问题就简化为对E中所有与活动1相容的活动进行活动安排的子问题。
- 若A是原问题的最优解,则A`=A-{1}是活动安排问题E’={i∈E : si ≥ f1}的最优解。
- 证明:如果能找到E’的一个解集B’,它包含比A’更多的活动,则将活动1加入到B`将产生A的一个解,它包含比A更多的活动,这与A的最优性矛盾!
- 因此:在做出贪心选择(活动1)之后,原问题N简化为:子问题N’:对E中所有与活动1相容的活动进行安排
每一步所做的贪心选择都将问题简化为一个更小的与原问题具有相同形式的子问题。
算法设计
- 用数组A[1:n]来存储所选择的活动(设活动总数为n),若活动i在集合A中,则A[i]=1,否则A[i]=0.
- 各活动的起始时间和结束时间存储于数组S[1:n]和F[1:n]中,数组F[1:n]已按结束时间的非减序排列。
- 依次从F[1:n]中选择活动i,尝试加入集合A,设:变量k记录A中最近一次加入的活动:由于F[1:n]有序,所以F[k]总是当前集合A中所有活动的最大结束时间。
- 依次检查活动i是否与当前已选择的所有活动相容,若相容则将活动i加入集合A中,若不相容,则放弃活动i。
- 继续检查F[1:n]中下一个活动与集合A中活动的相容性。
- 直到所有活动均已检查完毕,程序结束。
新增的活动i和当前集合A中所有活动相容的充分必要条件是
- S[i]≥F[k],活动i的开始时间不早于k的结束时间,k为最近加入集合A的活动,若条件满足,则活动i取代k成为最近加入的活动。
- 若S[i]<F[k],则放弃活动i,转而考虑下一个活动。
这种方式为后续活动预留尽可能多的时间
- 由于输入的活动按照其完成的时间非减序排列
- 所以每次总是选择具有最早完成时间的相容活动加入集合A
- 贪心选择的意义在于:使剩余的可安排时间段极大化,以便安排尽可能多的相容活动。
int greedySelector(int s[],int f[],int a[],int n){a[1] = 1;int j = 1;int count = 1;for(int i=2; i<=n; i++){if(s[i] >= f[j]){count++;j = i;a[i] = 1;}else{a[i] = 0;}}return count;
}
贪心算法求解背包问题
- 首先计算每种物品单位重量价值Vi/Wi
- 然后按照贪心选择策略:将尽可能多的单位重量价值最高的物品装入背包。
- 若将这种物品全部装入后,背包内的物品总重量未超过C
- 则选择单位重量价值次高的物品并尽可能多地装入背包
- 依次策略一直进行下去,直到背包装满为止。
算法复杂度分析:计算时间主要用于对各种物品按单位重量价值排序,因此算法的计算时间上界为O(nlogn)
对于0-1背包问题,贪心选择为什么不能得到最优解
- 因为对该问题采用贪心选择策略无法确保最终将背包装满
- 部分闲置的背包空间降低了每公斤背包空间的价值
最优装载问题
有一批集装箱要装船,其中:集装箱 i 的重量为wi ,轮船最大载重量为c,要求:在不受体积限制的情况下,将尽可能多的集装箱装船。
给定:c>0, wi>0, 1≤i≤n
要求:找出一个n元0/1向量x=(x1,x2,…,xn) 其中 xi∈{0,1}
时间复杂度O(nlogn)
void loading(int x[],int w[],int c,int n){int *R = (int *)malloc(sizeof(int)*(n+1));//根据w从小到大排序,数组R记录调整后的序号sort(w,R,n);for(int i=1; i<=n; i++){x[i] = 0;}for(int i=1; i<=n; i++){int id = R[i];if(w[id] > c){break;}x[id] = 1;c -= w[id];}
}
单源最短路径
单源最短路径 Single-Source Shortest Path (Dijkstra算法)
所有顶点对间的最短路径问题 All-Pairs Shortest paths (Floyd算法)
在有向图中,寻找从某个源点到其余各个顶点或者每一对顶点之间的最短带权路径的运算,称为最短路径问题。
单源最短路径问题
给定:带权有向图G=(V,E),其中:每条边的权是非负实数,给定顶点集合V中的一个顶点v,称为源点,求解:从源点v到G中其余各顶点之间的最短路径
Dijkstra算法是求解单源最短路径问题的一种有效算法
- 将图中所有顶点分成两组:S,V-S
- S:已确定最短路径的顶点的集合
- T=V-S:尚未确定最短路径的顶点集合
- 初始时,集合S中仅包含源点V0
- 不断在集合T中做贪心选择扩充集合S
- 直到S中包含了V中的所有顶点
算法设计思想:
- 初始时,S仅包含源v0
- 定义“特殊路径”:从源v0到G中某一顶点u且中间只经过S中顶点的路径称为从源到u的路径。
- 用数组元素dist[u]记录源v0到u的最短特殊路径的长度。
Dijkstra算法每次从T中取出具有最短特殊路径长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到其它所有顶点之间的最短路径长度。
Dijkstra算法的数据结构设计
- 使用带权邻接矩阵表示有向图G
- 辅助数组:Snvex:表示已找到从V0出发的最短路径的终点的集合。
- 辅助数组:dist[nvex]:存放当前找到的从V0到每个Vi的最短路径长度。
- 辅助数组:prev[next]:数组元素为从V0到路径各顶点的最短上该顶点的前一顶点的序号
算法伪代码:
- 令S={V0},T={其余顶点}
- T中顶点Vi对应的距离值dist[i]为:若存在<V0,Vi>:dist[i]为<V0,Vi>弧上的值;若不存在<V0,Vi>:dist[i]为∞
- 从T中选取一个dist矩阵值最小的顶点u加入S
- 对T中每一个顶点Vj的距离值dist[j]进行修改,若增加u作为中间顶点之后,从V0到Vj的距离比不加u的路径要短,则更新Vj距离值。
- 重复上述步骤,直到S中包含所有顶点(S=V)为止
void Dijkstra(int n,int v,int dist[],int prev[],int **c){int s[n];for(int i=1; i<=n; i++){dist[i] = c[v][i];s[i] = false;if(dist[i] == maxint){prev[i] = 0;}else{prev[i] = v;}}dist[v] = 0;s[v] = true;for(int i=1; i<n; i++){int temp = maxint;int u = v;for(int j=1; j<=n; j++){if(!s[j] && dist[j]<temp){u = j;temp = dist[j];}}s[u] = true;for(int j=1; j<=n ;j++){if(!s[j] && (c[u][j] < maxint)){int newdist = dist[u] + c[u][j];if(newdist < dist[j]){dist[j] = newdist;prev[j] = u;}}}}
}
算法复杂度分析:对于具有n个顶点和e条边的带权有向图G,需O(n2)
多机调度问题
设:有n个独立的作业{1,2…n},这n个作业由m台相同的机器进行加工处理,作业 i 所需要的执行时间为:ti,每个作业均可以在任何一个机器加工处理,但作业未完成之前不容许中断处理,作业也不能拆分为更小的子作业。
多机调度问题要求:给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
这个问题是NP完全问题,目前为止还没有十分有效的解法,用贪心选择策略有时可以设计出较好的近似算法。
具体来说:采用最长处理时间优先的贪心选择策略
- 当n≤m时,只要将机器i的[0,ti]时间区间分配给作业i即可。算法只需要O(1)时间
- n>m时,首先将n个作业依其所需的处理时间从大到小排序,然后依次顺序将作业分配给空闲的处理机,算法所需的计算时间为O(nlogn)

相关文章:

算法设计与分析期末考试复习(四)
贪心算法(Greedy Algorithm) 找零钱问题 假设有4种硬币,面值分别为:二角五分、一角、五分和一分,现在要找给顾客六角三分钱,如何找使得给出的硬币个数最少? 首先选出1个面值不超过六角三分的最…...
)
qsort函数排序数据 and 模拟实现qosrt函数(详解)
前言:内容包括使用库函数qsort排序任意类型的数据,模拟实现qsort函数(冒泡排序的逻辑) 我们先了解qsort函数的语法:qsort函数默认按照升序排序数据 void qsort (void* base, size_t num, size_t size,int (*compar)(…...

Mysql视图,存储过程,触发器,函数以及Mysql架构
一,视图视图是基于查询的一个虚拟表 , 也就是将sql语句封装起来, 要用的时候直接调用视图即可, select语句查询的表称为基表, 查询的结果集称为虚拟表, 基本表数据发生了改变, 那么视图也会发生改变, 使用视图就是为了简化查询语句.1.CREATE VIEW view_admin AS SELECT * FROM…...
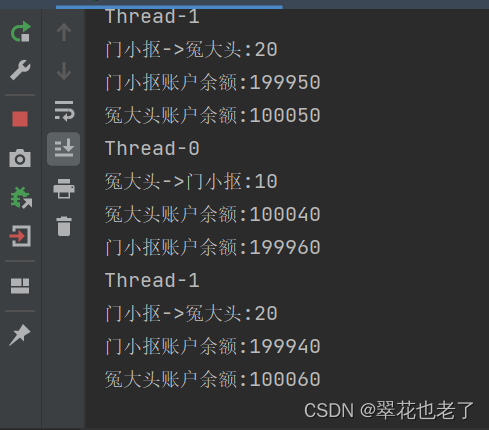
什么是线程死锁?如何解决死锁问题
死锁,一组互相竞争的资源的线程之间相互等待,导致永久阻塞的现象。 如下图所示: 与死锁对应的,还有活锁,是指线程没有出现阻塞,但是无限循环。 有一个经典的银行转账例子如下: 我们有个账户类…...
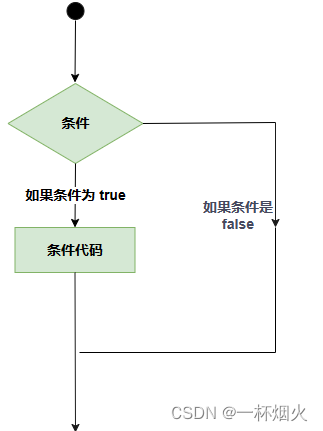
C语言几种判断语句简述
C 判断 判断结构要求程序员指定一个或多个要评估或测试的条件,以及条件为真时要执行的语句(必需的)和条件为假时要执行的语句(可选的)。 C 语言把任何非零和非空的值假定为 true,把零或 null 假定为 fals…...

【python学习笔记】:SQL常用脚本(二)
11、四舍五入ROUND函数 ROUND ( numeric_expression , length [ ,function ] ) function 必须为 tinyint、smallint 或 int。 如果省略 function 或其值为 0(默认值),则将舍入 numeric_expression。 如果指定了0以外的值,则将截…...

【Linux】进程地址空间
文章目录🎪 进程地址空间🚀1.写时拷贝与虚拟地址🚀2.地址空间引入🚀3.地址空间的意义⭐3.1 虚拟地址寻址⭐3.2 虚拟地址意义🎪 进程地址空间 地址空间(address space)表示任何一个计算机实体所…...

Qt音视频开发17-vlc内核回调拿图片进行绘制
一、前言 在众多播放器中,支持的种类格式众多,并支持DVD影音光盘,VCD影音光盘及各类流式协议,提供了sdk进行开发,这点是至关重要的,尽管很多优秀的播放器很牛逼,由于没有提供sdk第三方开发&…...

安装配置DHCP
本次实验采用CentOS71.检查在安装DHCP之前先使用rpm命令查看系统中已有的DHCP软件包rpm -qa | grep dhcp由此可知,系统中尚未安装DHCP软件包2.安装我们可以使用yum命令为系统安装DHCP软件包yum -y install dhcp安装完成后再次检查可以看到DHCP软件包3.配置dhcp配置文…...

MarkDown中写UML图的方法
目录序UML图之顺序图顺序图的四个要素关于消息箭头的语法Mermaid中顺序图的简单例子样例用小人表示对象为对象设置别名激活对象UML图之类图类图中常见的关系关于不同类型关系的语法Mermaid中类图的简单例子样例类定义的两种方式为类定义成员双向关系的表示多重性关系的表示UML之…...

Axure8设计—动态仪表盘
本次分享的的案例是Axure8制作的动态仪表盘,根据设置的数值,仪表盘指针旋转到相应的值位置 预览地址:https://2qiuwg.axshare.com 下载地址:https://download.csdn.net/download/weixin_43516258/87502161 一、制作原型 1、首先创建空白页…...
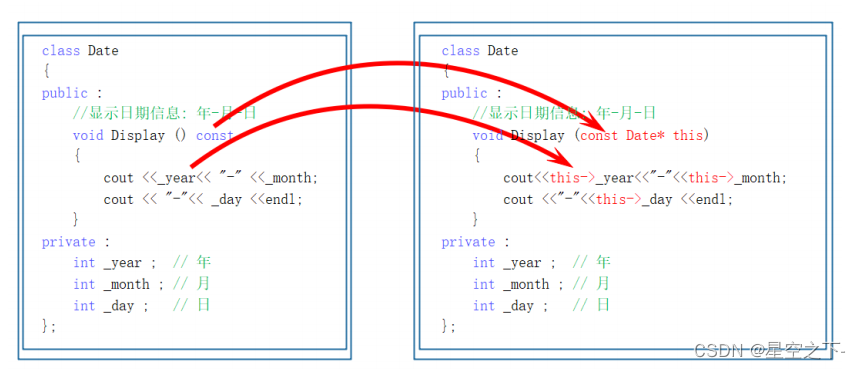
【C++】类和对象的六个默认成员函数
类的6个默认成员函数构造函数概念特性析构函数概念特性拷贝构造函数概念特征拷贝构造函数典型调用场景:赋值运算符重载运算符重载赋值运算符重载取地址及const取地址操作符重载类的6个默认成员函数 到底什么是类的6个默认成员函数呢?相信大家一定对此怀…...
4、算法MATLAB---认识矩阵
认识矩阵1、矩阵定义和基本运算1.1 赋值运算符:1.2 等号运算符:1.3 空矩阵1.4 一行一列矩阵1.5 行矩阵(元素用空格或逗号分隔)1.6 列矩阵(分号表示换行)1.7 m行n列的矩阵:行值用逗号间隔&#x…...
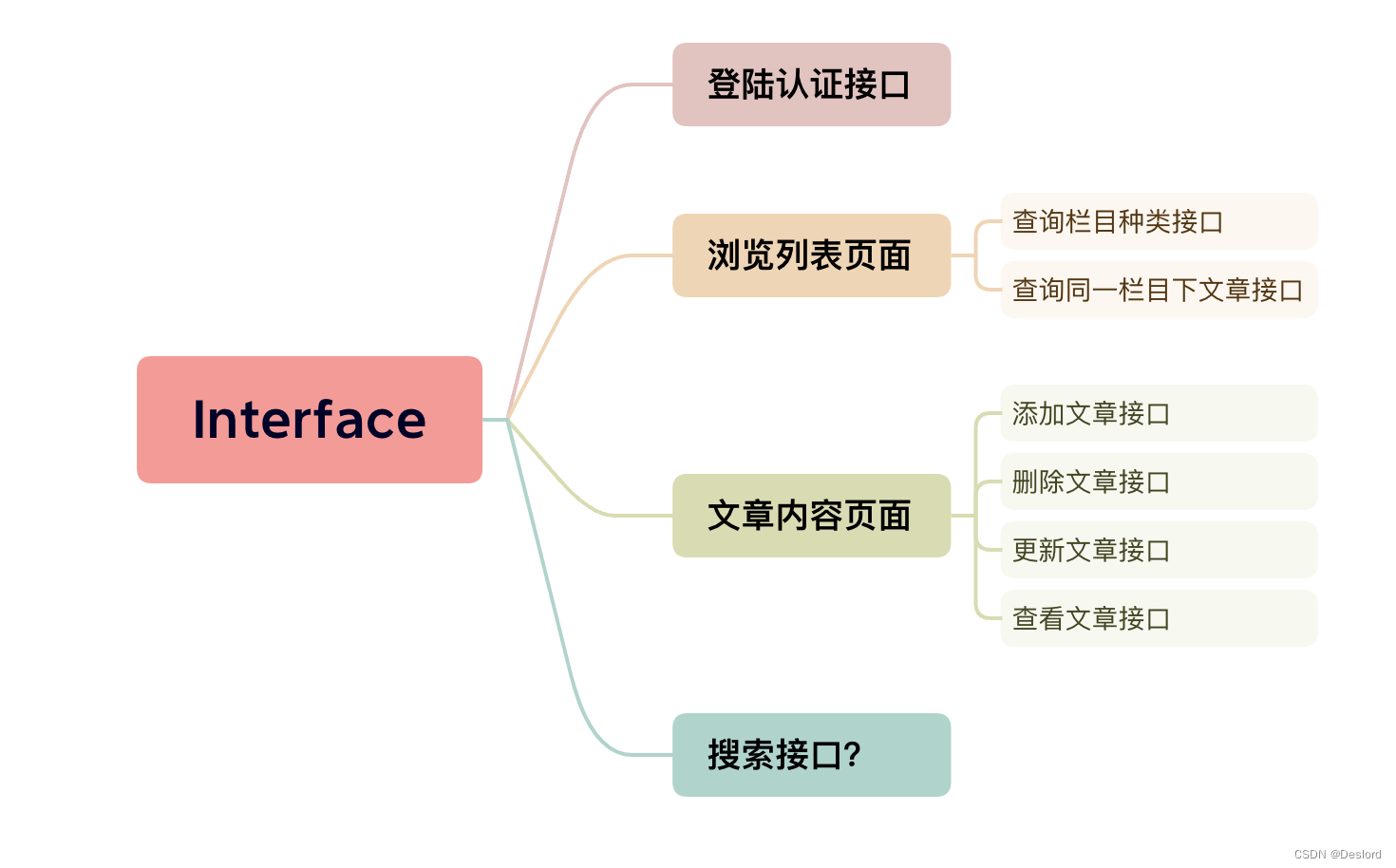
vue3+rust个人博客建站日记2-确定需求
反思 有人说过我们正在临近代码的终结点。很快,代码就会自动产生出来,不需要再人工编写。程序员完全没用了,因为商务人士可以从规约直接生成程序。 扯淡!我们永远抛不掉代码,因为代码呈现了需求的细节。在某些层面上&a…...

Linux安装云原生网关Kong/KongA
目录1 概述2 创建服务器3 安装postgres4 安装kong5 安装node6 安装KONGA1 概述 Kong Kong是一款基于OpenResty(NginxLua模块)编写的高可用、易扩展的开源API网关,专为云原生和云混合架构而建,并针对微服务和分布式架构进行了特别…...
)
Vue学习笔记(2)
2.1 事件处理 2.1.1 事件监听器 JavaScript:通过获取DOM对象再往DOM对象上使用addEventListener注册监听事件 const btn document.querySelector(#my-button) btn.addEventListener(click, function() {alert(点击事件!) })jQuery:通过$选择器绑定对象…...

2023年三月份图形化四级打卡试题
活动时间 从2023年3月1日至3月21日,每天一道编程题。 本次打卡的规则如下: 小朋友每天利用10~15分钟做一道编程题,遇到问题就来群内讨论,我来给大家答疑。 小朋友做完题目后,截图到朋友圈打卡并把打卡的截图发到活动群…...

Python操作Excel
Python中对Excel文件的操作包括:读、写、修改。如果要对其进行如上的操作需要导入Python的第三方模块:xlrd、xlwd、xlutils,其分别对应Python的读、写、修改的操作 一、安装Python的第三方模块 二、操作Excel的基本步骤 1、导入响对应的模…...
 C. Serval and Toxel‘s Arrays【统计次数,算贡献】)
Codeforces Round #853 (Div. 2) C. Serval and Toxel‘s Arrays【统计次数,算贡献】
链接 传送门 分析 这道题想法其实很简单,样例的计算方法一定要看懂。以样例1为例,根据他的操作方法可以得到两个新的数组,和一个原来的数组,总共三个数组。 1 2 3 4 2 3 4 5 3 他们两两配对去重,求出总的value。由于每…...
微信小程序-1:比较两数的大小
程序来源》微信小程序开发教程(第二章) 主编:黄寿孟、易芳、陶延涛 ISBN: 9787566720788 程序运行结果: <!--index.wxml--> <view class"container"> <text>第一个数字:&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
