Codeforces Round #853 (Div. 2) C. Serval and Toxel‘s Arrays【统计次数,算贡献】
链接
传送门
分析
这道题想法其实很简单,样例的计算方法一定要看懂。以样例1为例,根据他的操作方法可以得到两个新的数组,和一个原来的数组,总共三个数组。
1 2 3
4 2 3
4 5 3
他们两两配对去重,求出总的value。由于每个数组内的各个数各不相同,也就是对于某个数字在一个数组内最多出现一次,只需要统计一下这个数出现的次数就可以知道这个数在多少个数组内,假设我们已经统计到了这个数的出现次数记作m,数组总数记作n,那么在所有的配对中,这个数字的贡献是多少?
包含这个数字的配对有两种,一种是两个都是这个数,一种是只有一个这个数,例如4的贡献,一种是4-4, 另一种是4-1,4-1。其他的配对不含4没有4的贡献。
取一个数的贡献是这个数个数乘以其他数的个数,即m(n−m)取一个数的贡献是这个数个数乘以其他数的个数,即m(n-m)取一个数的贡献是这个数个数乘以其他数的个数,即m(n−m)
取两个相同的个数的数是Cm2取两个相同的个数的数是C^2_m取两个相同的个数的数是Cm2
故总贡献是Cm2+m(n−m)故总贡献是C^2_m+m(n-m)故总贡献是Cm2+m(n−m)
如何着手统计。
我们发现,每次更新都会另起一段,这些出现的次数都是一段一段的,所以我们开一个数组记录上一次更新的位置,每次另一起一段的时候更新位置,并把旧的一段统计如数组即可。注意,最后残余的要清理干净。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 4e5 + 5;
int cnt[N], st[N], a[N];
void solve() {int n, m;cin >> n >> m;for (int i = 1; i <= n + m; i++) cnt[i] = 0, st[i] = 0;for (int i = 1; i <= n; i++) {int c;cin >> c;a[i] = c;}for (int i = 1; i <= m; i++) {int p, v;cin >> p >> v;if (v != a[p]) cnt[a[p]] += i - st[p], st[p] = i;//一定要不等于a[p] = v;}for (int i = 1; i <= n; i++) {//残余部分cnt[a[i]] += m - st[i] + 1;//坐标相减要加1}ll ans = 0;for (int i = 1; i <= n + m; i++) {ans += 1ll * cnt[i] * (m + 1 - cnt[i]);ans += 1ll * cnt[i] * (cnt[i] - 1) / 2;}cout << ans << '\n';
}
int main(){ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) solve();return 0;
}相关文章:
 C. Serval and Toxel‘s Arrays【统计次数,算贡献】)
Codeforces Round #853 (Div. 2) C. Serval and Toxel‘s Arrays【统计次数,算贡献】
链接 传送门 分析 这道题想法其实很简单,样例的计算方法一定要看懂。以样例1为例,根据他的操作方法可以得到两个新的数组,和一个原来的数组,总共三个数组。 1 2 3 4 2 3 4 5 3 他们两两配对去重,求出总的value。由于每…...
微信小程序-1:比较两数的大小
程序来源》微信小程序开发教程(第二章) 主编:黄寿孟、易芳、陶延涛 ISBN: 9787566720788 程序运行结果: <!--index.wxml--> <view class"container"> <text>第一个数字:&…...
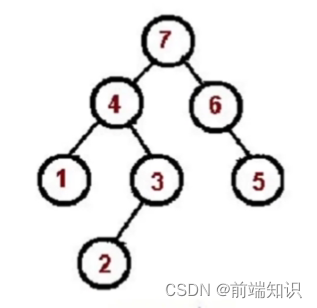
数据结构——树
深度优先/广度优先遍历深度优先:访问根节点对根节点的 children 挨个进行深度优先遍历const tree {val: "a",children: [{val: "b",children: [{val: "d",children: [],},{val: "e",children: [],},],},{val: "c&quo…...

【华为OD机试模拟题】用 C++ 实现 - 找到它(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 去重求和(2023.Q1) 文章目录 最近更新的博客使用说明找到它题目输入输出示例一输入输出示例二输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD …...

python中yield的使用
在 Python 中,yield 是一个关键字,它用于定义生成器函数。生成器函数是一个特殊的函数,可以返回一个迭代器,当生成器函数被调用时,它不会立即执行,而是返回一个生成器对象,通过迭代生成器对象可…...
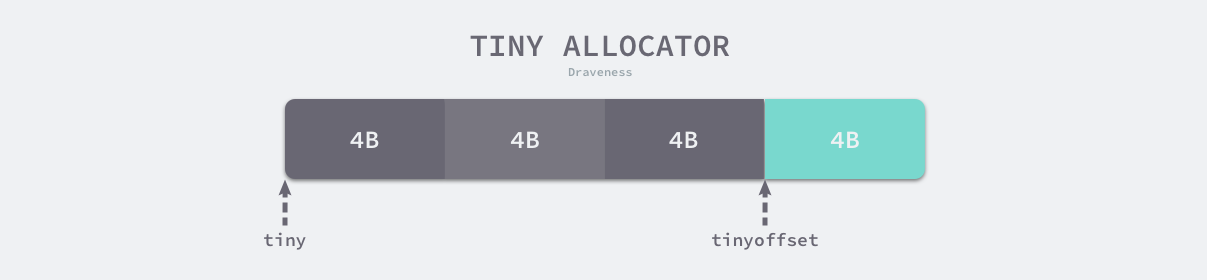
GO进阶(4) 深入Go的内存管理
Go语言成为高生产力语言的原因之一自己管理内存:Go抛弃了C/C中的开发者管理内存的方式,实现了主动申请与主动释放管理,增加了逃逸分析和GC,将开发者从内存管理中释放出来,让开发者有更多的精力去关注软件设计ÿ…...
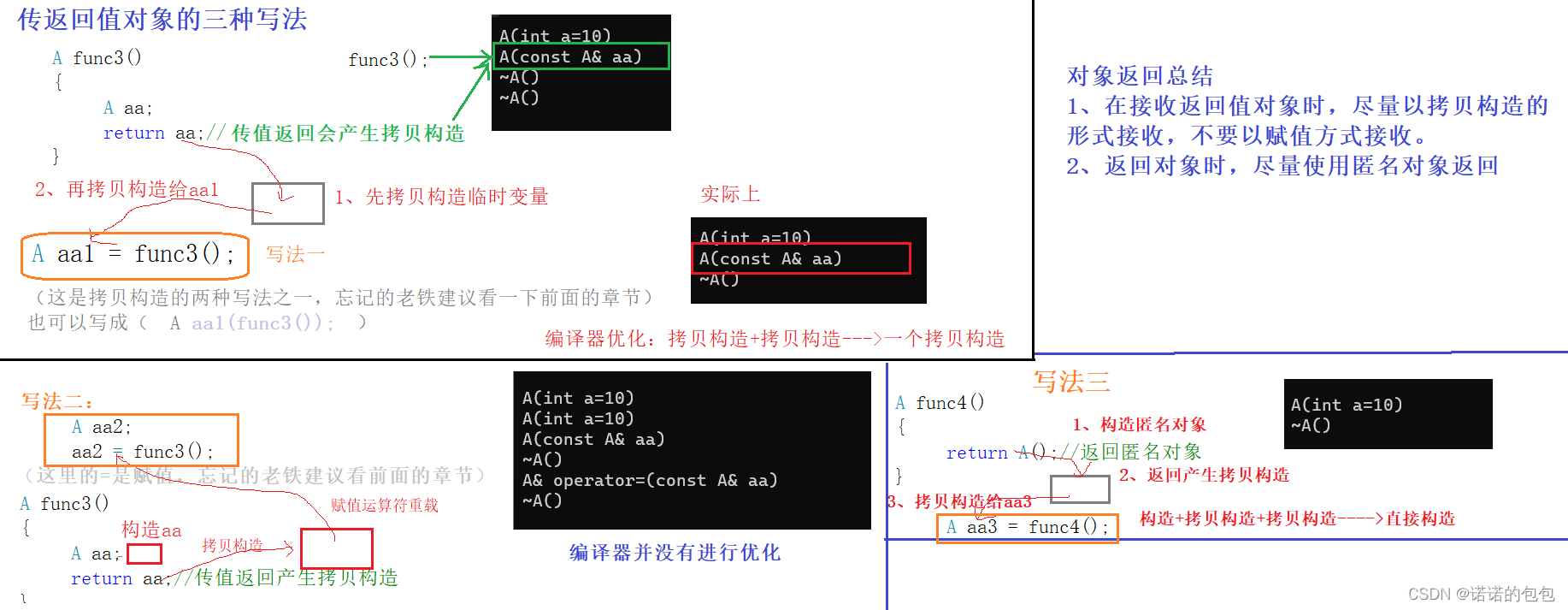
【C++】类与对象理解和学习(下)
放在专栏【C知识总结】,会持续更新,期待支持🌹建议先看完【C】类与对象理解和学习(上)【C】类与对象理解和学习(中)本章知识点概括Ⅰ本章知识点概括Ⅱ初始化列表前言在上一篇文章中,…...

【Neo4j】Spring Data Neo4j APi阅读随笔
引言 关于Spring boot整合Neo4j的官方api翻译&学习随笔 (TOC) 一、准备工作 1.注入依赖 <dependency><groupId>org.springframework.data</groupId><artifactId>spring-data-jpa</artifactId></dependency>2.配置yml文件 这里是本…...

JVM内存模型简介
1 程序计数器 程序计数器是一块较小的内存空间,可以看作是当前线程所执行的字节码的行号指示器。字节码解释器工作时通过改变这个计数器的值来选取下一条需要执行的字节码指令,分支、循环、跳转、异常处理、线程恢复等功能都需要依赖这个计数器来完。 ja…...

k8s如何给node添加标签
一、为什么需要标签? k8s集群如果由大量节点组成,可将节点打上对应的标签,然后通过标签进行筛选及查看,更好的进行资源对象的相关选择与匹配 二、怎么查看目前node上具有的标签 [rootmaster01 ~]# kubectl get node --show-labels NAME …...
【大数据Hive】Hive ddl语法使用详解
一、前言 使用过关系型数据库mysql的同学对mysql的ddl语法应该不陌生,使用ddl语言来创建数据库中的表、索引、视图、存储过程、触发器等,hive中也提供了类似ddl的语法。本篇将详细讲述hive中ddl的使用。 二、hive - ddl 整体概述 在Hive中,DA…...
)
Connext DDS录制服务 Recording Service(2)
2.4 远程管理 控制客户端(如RTI管理控制台)可以使用此接口远程控制录制服务。 注:记录服务远程管理基于第10.3节中描述的RTI远程管理平台。有关录制服务中远程管理工作的详细讨论,请参阅该手册 下面是所有支持操作的API引用。 2.4.1 启用远程管理 默认情况下,在录制服务中…...

mysql数据类型选择
数据类型选择 完整性约束 是完整性约束是为保证数据库中数据的正确性和相容性,对关系模型提出的某种约束条件或规则。 通常包括:实体完整性约束、参照完整性约束、域完整性约束、用户自定义完整性约束。 实体完整性(Entity integrity)是指主键必须非空…...

【Java】Spring Boot 配置文件
文章目录SpringBoot 配置文件1. 配置文件的作用2. 配置文件的格式3. properties配置文件说明3.1 properties基本语法3.2 读取配置文件3.3 properties缺点分析4. yml配置文件说明4.1 yml基本语法4.2 yml使用进阶4.2.1 yml配置不同的数据类型及null4.2.1 yml配置的读取4.2.2 配置…...
AtCoder Beginner Contest 290 G. Edge Elimination(思维题 枚举+贪心)
题目 T(T<100)组样例,每次给出一棵深度为d的k叉树, 其中,第i层深的节点个数为 保证k叉树的所有节点个数tot不超过1e18, 求在k叉树上构建一棵大小恰为x的连通块,所需要断开的最少的树边的条数(x<tot<1e18)…...
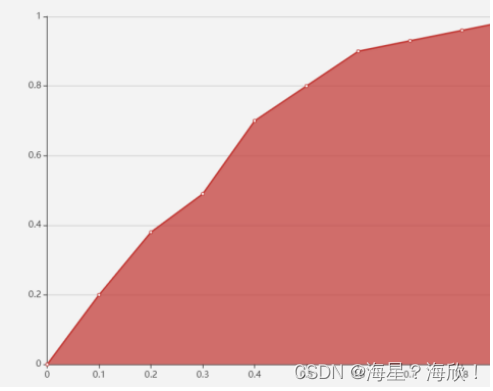
数据挖掘概述
目录1、数据挖掘概述2、数据挖掘常用库3、模型介绍3.1 分类3.2 聚类3.3 回归3.4 关联3.5 模型集成4、模型评估ROC 曲线5、模型应用1、数据挖掘概述 数据挖掘:寻找数据中隐含的知识并用于产生商业价值 数据挖掘产生原因:海量数据、维度众多、问题复杂 数…...

linux kernel iio 架构
linux kernel iio 架构讲解Linux IIO(Industrial I/O)架构是Linux内核提供的一种用于支持各种类型传感器和数据采集设备的子系统,包括温度、压力、湿度、加速度、光度等多种传感器。IIO架构的核心是一个通用的IIO子系统,它提供了一…...

Socket通信详解
Socket通信详解 文章目录Socket通信详解Socket流程介绍函数介绍编程实例Socket流程介绍 socket通信类似于电话通信,其服务器基本流程就是 Created with Raphal 2.3.0安装电话socket()分配电话号码bind()连接电话线listen()拿起话筒accept()函数介绍 socket() 其中…...
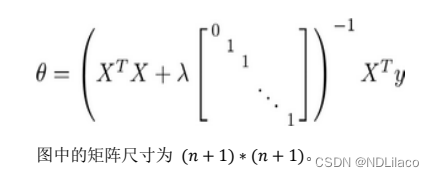
多分类、正则化问题
多分类问题 利用逻辑回归解决多分类问题,假如有一个训练集,有 3 个类别,分别为三角形 𝑦 1,方框𝑦 2,圆圈 𝑦 3。我们下面要做的就是使用一个训练集,将其分成 3 个二…...

史上最全面的软件测试面试题总结(接口、自动化、性能全都有)
目录 思维发散 Linux 测试概念和模型 测试计划与工具 测试用例设计 Web项目 Python基础 算法 逻辑 接口测试 性能测试 总结感谢每一个认真阅读我文章的人!!! 重点:配套学习资料和视频教学 思维发散 一个球ÿ…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
