数据结构——树
深度优先/广度优先遍历
深度优先:
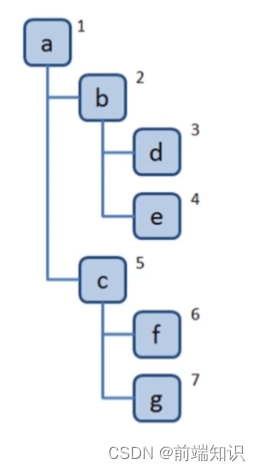
访问根节点
对根节点的 children 挨个进行深度优先遍历
const tree = {val: "a",children: [{val: "b",children: [{val: "d",children: [],},{val: "e",children: [],},],},{val: "c",children: [{val: "f",children: [],},{val: "g",children: [],},],},],
};const dfs = (root) => {console.log(root.val);root.children.forEach((child) => {dfs(child);});
};dfs(tree);广度优先:
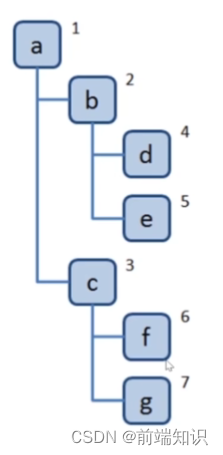
新建立一个队列,根节点入队
对头出队并访问
把对头的children挨个入队
重复2,3,直到队列为空
const tree = {val: "a",children: [{val: "b",children: [{val: "d",children: [],},{val: "e",children: [],},],},{val: "c",children: [{val: "f",children: [],},{val: "g",children: [],},],},],
};const bfs = (root) => {const q = [root];while (q.length > 0) {const n = q.shift();console.log(n.val);n.children.forEach((child) => {q.push(child);});}
};bfs(tree);二叉树的先中后序遍历
二叉树:每个节点最多只能有两个节点
先序遍历(根、左、右):
访问根节点
对根节点的左子树进行先序遍历
对根节点的右子树进行先序遍历
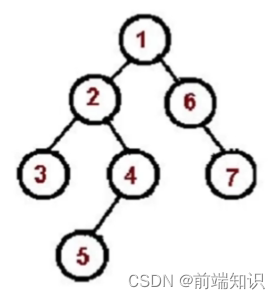
1、2、3、4、5、6、7
const tree = {val: "1",left: {val: "2",left: {val: "3",left: null,right: null,},right: {val: "4",left: {val: "5",},right: null,},},right: {val: "6",left: null,right: {val: "7",right: null,left: null,},},
};const preorder = (root) => {if (!root) return;console.log(root.val);preorder(root.left);preorder(root.right);
};
preorder(tree);中序遍历(左、中、右):
对根节点左子树遍历
访问根节点
对根节点右子树遍历
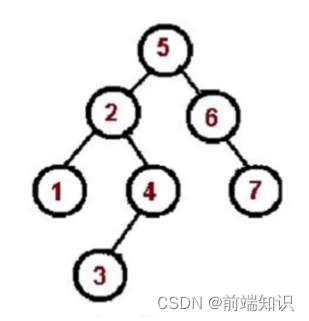
1、2、3、4、5、6、7
const tree = {val: "5",left: {val: "2",left: {val: "1",left: null,right: null,},right: {val: "4",left: {val: "3",},right: null,},},right: {val: "6",left: null,right: {val: "7",right: null,left: null,},},
};const inorder = (root) => {if (!root) return;inorder(root.left);console.log(root.val);inorder(root.right);
};
inorder(tree);后序遍历(左、右、根):
对根节点左子树遍历
对根节点右子树遍历
访问根节点
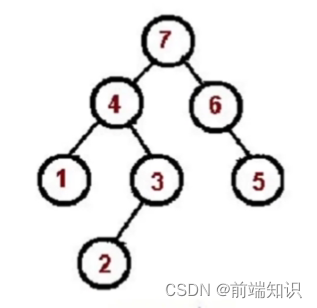
1、2、3、4、5、6、7
const tree = {val: "7",left: {val: "4",left: {val: "1",left: null,right: null,},right: {val: "3",left: {val: "2",},right: null,},},right: {val: "6",left: null,right: {val: "5",right: null,left: null,},},
};const postorder = (root) => {if (!root) return;postorder(root.left);postorder(root.right);console.log(root.val);
};
postorder(tree);非递归写法
递归调用函数,会不断的入栈出栈,所以考虑用栈实现。
先序遍历:
// 递归
const preorder = (root) => {if (!root) return;console.log(root.val);preorder(root.left);preorder(root.right);
};// 非递归
const preorder = (root) => {if (!root) return;const stack = [root]while(stack.length){const n = stack.pop()console.log(n.val)// 栈后进先出,先右后左if(n.right) stack.push(n.right)if(n.left) stack.push(n.left)}
}中序遍历:
// 递归
const inorder = (root) => {if (!root) return;inorder(root.left);console.log(root.val);inorder(root.right);
};
// 非递归
const inorder = (root) => {if (!root) return;const stack = [];let p = root;while (stack.length || p) {// 所有的左子树进栈while (p) {stack.push(p);p = p.left;}//最尽头的左子树出栈const n = stack.pop();console.log(n.val);p = n.right;}
};后续遍历:
const postorder = (root) => {if (!root) return;postorder(root.left);postorder(root.right);console.log(root.val);
};
// 先序遍历是 根、左、右,后续遍历时:左、右、根,倒过来是根、右、左,只需要把先序遍历的后面两个颠倒顺序const postorder = (root) => {if (!root) return;const outputStack = [];const stack = [root];while (stack.length) {const n = stack.pop();outputStack.push(n);if (n.left) stack.push(n.left);if (n.right) stack.push(n.right);}while (outputStack.length) {const n = outputStack.pop();console.log(n.val);}
};相关文章:

数据结构——树
深度优先/广度优先遍历深度优先:访问根节点对根节点的 children 挨个进行深度优先遍历const tree {val: "a",children: [{val: "b",children: [{val: "d",children: [],},{val: "e",children: [],},],},{val: "c&quo…...

【华为OD机试模拟题】用 C++ 实现 - 找到它(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 去重求和(2023.Q1) 文章目录 最近更新的博客使用说明找到它题目输入输出示例一输入输出示例二输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD …...

python中yield的使用
在 Python 中,yield 是一个关键字,它用于定义生成器函数。生成器函数是一个特殊的函数,可以返回一个迭代器,当生成器函数被调用时,它不会立即执行,而是返回一个生成器对象,通过迭代生成器对象可…...
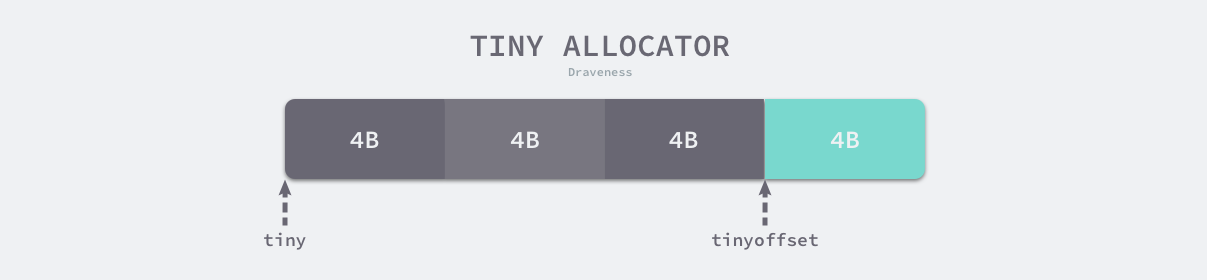
GO进阶(4) 深入Go的内存管理
Go语言成为高生产力语言的原因之一自己管理内存:Go抛弃了C/C中的开发者管理内存的方式,实现了主动申请与主动释放管理,增加了逃逸分析和GC,将开发者从内存管理中释放出来,让开发者有更多的精力去关注软件设计ÿ…...
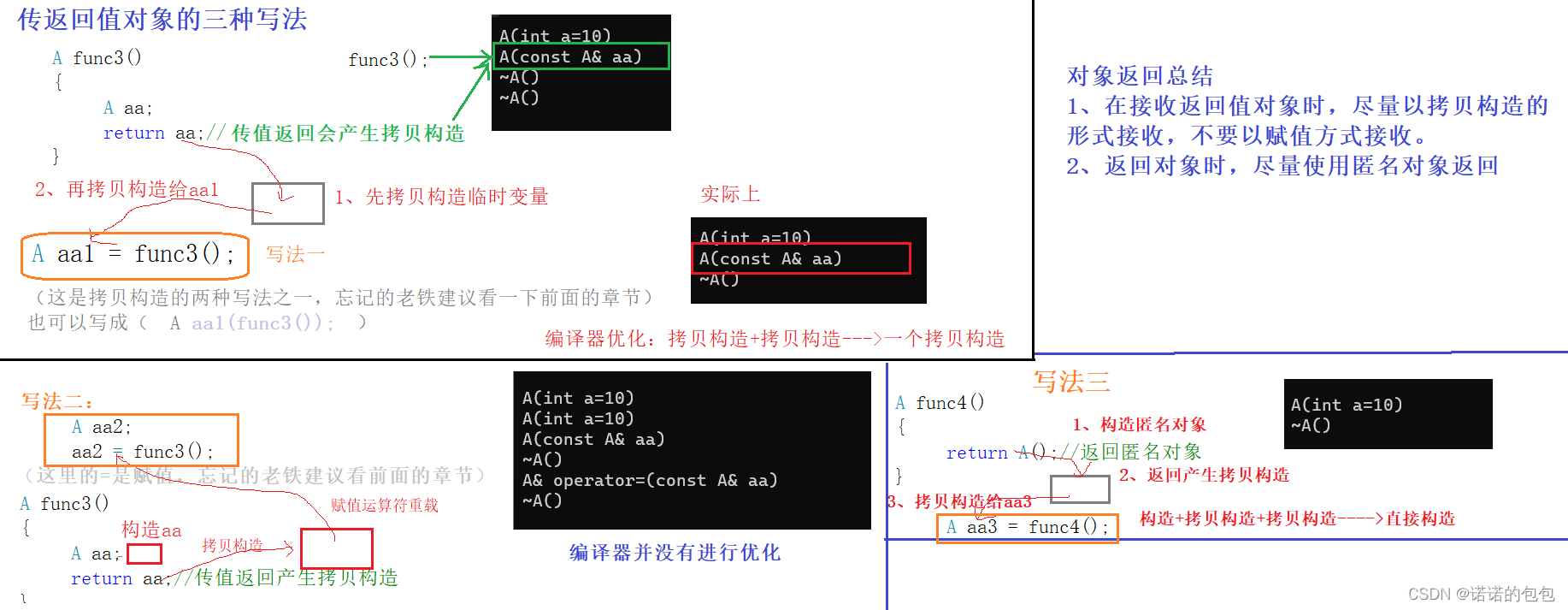
【C++】类与对象理解和学习(下)
放在专栏【C知识总结】,会持续更新,期待支持🌹建议先看完【C】类与对象理解和学习(上)【C】类与对象理解和学习(中)本章知识点概括Ⅰ本章知识点概括Ⅱ初始化列表前言在上一篇文章中,…...

【Neo4j】Spring Data Neo4j APi阅读随笔
引言 关于Spring boot整合Neo4j的官方api翻译&学习随笔 (TOC) 一、准备工作 1.注入依赖 <dependency><groupId>org.springframework.data</groupId><artifactId>spring-data-jpa</artifactId></dependency>2.配置yml文件 这里是本…...

JVM内存模型简介
1 程序计数器 程序计数器是一块较小的内存空间,可以看作是当前线程所执行的字节码的行号指示器。字节码解释器工作时通过改变这个计数器的值来选取下一条需要执行的字节码指令,分支、循环、跳转、异常处理、线程恢复等功能都需要依赖这个计数器来完。 ja…...

k8s如何给node添加标签
一、为什么需要标签? k8s集群如果由大量节点组成,可将节点打上对应的标签,然后通过标签进行筛选及查看,更好的进行资源对象的相关选择与匹配 二、怎么查看目前node上具有的标签 [rootmaster01 ~]# kubectl get node --show-labels NAME …...
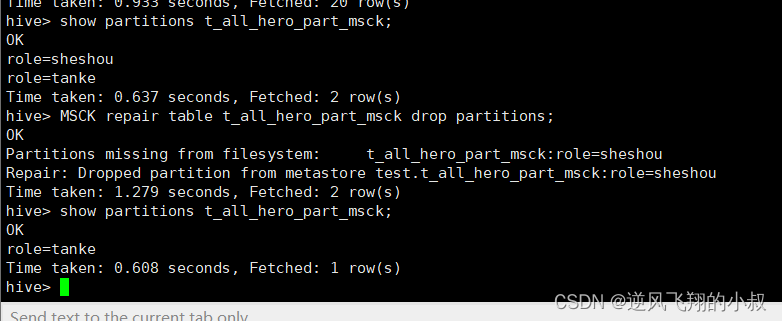
【大数据Hive】Hive ddl语法使用详解
一、前言 使用过关系型数据库mysql的同学对mysql的ddl语法应该不陌生,使用ddl语言来创建数据库中的表、索引、视图、存储过程、触发器等,hive中也提供了类似ddl的语法。本篇将详细讲述hive中ddl的使用。 二、hive - ddl 整体概述 在Hive中,DA…...
)
Connext DDS录制服务 Recording Service(2)
2.4 远程管理 控制客户端(如RTI管理控制台)可以使用此接口远程控制录制服务。 注:记录服务远程管理基于第10.3节中描述的RTI远程管理平台。有关录制服务中远程管理工作的详细讨论,请参阅该手册 下面是所有支持操作的API引用。 2.4.1 启用远程管理 默认情况下,在录制服务中…...

mysql数据类型选择
数据类型选择 完整性约束 是完整性约束是为保证数据库中数据的正确性和相容性,对关系模型提出的某种约束条件或规则。 通常包括:实体完整性约束、参照完整性约束、域完整性约束、用户自定义完整性约束。 实体完整性(Entity integrity)是指主键必须非空…...

【Java】Spring Boot 配置文件
文章目录SpringBoot 配置文件1. 配置文件的作用2. 配置文件的格式3. properties配置文件说明3.1 properties基本语法3.2 读取配置文件3.3 properties缺点分析4. yml配置文件说明4.1 yml基本语法4.2 yml使用进阶4.2.1 yml配置不同的数据类型及null4.2.1 yml配置的读取4.2.2 配置…...
AtCoder Beginner Contest 290 G. Edge Elimination(思维题 枚举+贪心)
题目 T(T<100)组样例,每次给出一棵深度为d的k叉树, 其中,第i层深的节点个数为 保证k叉树的所有节点个数tot不超过1e18, 求在k叉树上构建一棵大小恰为x的连通块,所需要断开的最少的树边的条数(x<tot<1e18)…...
数据挖掘概述
目录1、数据挖掘概述2、数据挖掘常用库3、模型介绍3.1 分类3.2 聚类3.3 回归3.4 关联3.5 模型集成4、模型评估ROC 曲线5、模型应用1、数据挖掘概述 数据挖掘:寻找数据中隐含的知识并用于产生商业价值 数据挖掘产生原因:海量数据、维度众多、问题复杂 数…...

linux kernel iio 架构
linux kernel iio 架构讲解Linux IIO(Industrial I/O)架构是Linux内核提供的一种用于支持各种类型传感器和数据采集设备的子系统,包括温度、压力、湿度、加速度、光度等多种传感器。IIO架构的核心是一个通用的IIO子系统,它提供了一…...

Socket通信详解
Socket通信详解 文章目录Socket通信详解Socket流程介绍函数介绍编程实例Socket流程介绍 socket通信类似于电话通信,其服务器基本流程就是 Created with Raphal 2.3.0安装电话socket()分配电话号码bind()连接电话线listen()拿起话筒accept()函数介绍 socket() 其中…...
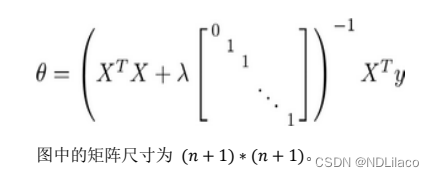
多分类、正则化问题
多分类问题 利用逻辑回归解决多分类问题,假如有一个训练集,有 3 个类别,分别为三角形 𝑦 1,方框𝑦 2,圆圈 𝑦 3。我们下面要做的就是使用一个训练集,将其分成 3 个二…...

史上最全面的软件测试面试题总结(接口、自动化、性能全都有)
目录 思维发散 Linux 测试概念和模型 测试计划与工具 测试用例设计 Web项目 Python基础 算法 逻辑 接口测试 性能测试 总结感谢每一个认真阅读我文章的人!!! 重点:配套学习资料和视频教学 思维发散 一个球ÿ…...

速来~与 Werner Vogels 博士一起探索敏捷性与创新速度一起提升的秘方
Amazon Web Services 的现代应用程序创新一直是 Amazon 公司坚持追求的核心目标。约20年前,我们经历了一次彻底的转型,旨在建立起“发明、发布、再发明、再发布、重新开始、洗牌、再重复”的快速迭代流程。正是此番探索,彻底改变了我们构建应…...

Apache Hadoop、HDFS介绍
目录Hadoop介绍Hadoop集群HDFS分布式文件系统基础文件系统与分布式文件系统HDFS简介HDFS shell命令行HDFS工作流程与机制HDFS集群角色与职责HDFS写数据流程(上传文件)HDFS读数据流程(下载文件)Hadoop介绍 用Java语言实现开源 允许…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
