C++前缀和算法的应用:统计上升四元组
C++前缀和算法的应用:统计上升四元组
本文涉及的基础知识点
C++算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频
题目
给你一个长度为 n 下标从 0 开始的整数数组 nums ,它包含 1 到 n 的所有数字,请你返回上升四元组的数目。
如果一个四元组 (i, j, k, l) 满足以下条件,我们称它是上升的:
0 <= i < j < k < l < n 且
nums[i] < nums[k] < nums[j] < nums[l] 。
示例 1:
输入:nums = [1,3,2,4,5]
输出:2
解释:
- 当 i = 0 ,j = 1 ,k = 2 且 l = 3 时,有 nums[i] < nums[k] < nums[j] < nums[l] 。
- 当 i = 0 ,j = 1 ,k = 2 且 l = 4 时,有 nums[i] < nums[k] < nums[j] < nums[l] 。
没有其他的四元组,所以我们返回 2 。
示例 2:
输入:nums = [1,2,3,4]
输出:0
解释:只存在一个四元组 i = 0 ,j = 1 ,k = 2 ,l = 3 ,但是 nums[j] < nums[k] ,所以我们返回 0 。
参数范围:
4 <= nums.length <= 4000
1 <= nums[i] <= nums.length
nums 中所有数字 互不相同 ,nums 是一个排列。
容易理解
分析
第一层循环,枚举j,第二层循环枚举k。时间复杂度O(n*n)。在通过不通过之间,用vector<vector>就通过不了,用int**勉强可以通过。分两步:
| 第一步 | 求前缀和 |
| 第二步 | 枚举j和k |
核心代码
class Solution {
public:
long long countQuadruplets(vector& nums) {
m_c = nums.size();
int** vSum = new int*[m_c + 1];//vSum[i][j]:nums[0,j)中小于等于i的个数
for (int i = 1; i <= m_c; i++)
{//计算小于i的个数
vSum[i] = new int[m_c+1];
vSum[i][0] = 0;
for (int j = 0 ; j < m_c; j++ )
{
vSum[i][j+1] = vSum[i][j] + (nums[j] <= i);
}
}
long long llRet = 0;
for (int j = 1; j < m_c; j++)
{
for (int k = j + 1; k+1 < m_c; k++)
{
if (nums[j] < nums[k])
{
continue;
}
//nums[i]范围:nums[0,j)中小于等于nums[k]的数量
const long long lessNumK = vSum[nums[k]][j];
//nums[k+1,m_c)中大于nums[j]
const long long moreNumJ = m_c - (k + 1) - (vSum[nums[j]][m_c]- vSum[nums[j]][k+1]);
llRet += lessNumK * moreNumJ;
}
}
return llRet;
}
int m_c;
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
Solution slu;
vector nums ;
long long res;
nums = { 1, 3, 2, 4, 5 };
res = slu.countQuadruplets(nums);
Assert(2LL, res);
nums = { 1, 2,3,4 };
res = slu.countQuadruplets(nums);
Assert(0LL, res);
nums = { 4,3,2,1 };
res = slu.countQuadruplets(nums);
Assert(0LL, res);
nums = { 4,3,2,6,5,1 };
res = slu.countQuadruplets(nums);
Assert(0LL, res);
nums = { 1,3,2,4 };
res = slu.countQuadruplets(nums);
Assert(1LL, res);
nums = { 2,1,4,3,5 };
res = slu.countQuadruplets(nums);
Assert(2LL, res);
nums.clear();
for (int i = 0; i < 4000; i++)
{
nums.emplace_back(i + 1);
}
res = slu.countQuadruplets(nums);
Assert(0LL, res);
//CConsole::Out(res);
}
性能稍强
分析
第一层循环,枚举l或k;第二层循环,枚举j。时间复杂度O(n*n),代码简洁得多,可以轻松通过。
变量解释
| llRet | 所有符合条件的四元祖 |
| iLessLK | nums[0,j)中小于nums[i]的数量 |
| m_v132[j] | nums[0,i)中符合i,j,k的数量 |
核心代码
class Solution {
public:long long countQuadruplets(vector<int>& nums) {m_c = nums.size();long long llRet = 0;vector<long long> m_v132(m_c);//132for (int lk = 0; lk < m_c; lk++){int iLessLK = 0;for (int j = 0; j < lk; j++){if (nums[j] < nums[lk]){iLessLK++;llRet += m_v132[j];}else{//iLessLK 表示[0,j)中小于nums[lk]的数,假定其索引为i,则nums[i] < nums[lk] ,nums[j] < nums[lk],故i j lk,符合前三个数i,j,km_v132[j] += iLessLK;}}}return llRet;}int m_c;
};
2月旧代码
class Solution {
public:
long long countQuadruplets(vector& nums) {
m_c = nums.size();
//vLeft[i][m] 表示nums[i]及之前的元素,小于等于m+1的个数
int vLeft[4000][4000] = { 0 };
{
for (int i = 0; i < m_c; i++)
{
if (i > 0)
{
memcpy(vLeft[i], vLeft[i - 1], sizeof(vLeft[0]));
}
for (int j = nums[i] - 1; j < m_c; j++)
{
vLeft[i][j] ++;
}
}
}
long long llRet = 0;
for (int j = 1; j + 1 < m_c; j++)
{
for (int k = j + 1; k + 1 < m_c; k++)
{
if (nums[j] <= nums[k])
{
continue;
}
const int iLeft = vLeft[j - 1][nums[k] - 1];
const int iRight = nums[j] - vLeft[k][nums[j] - 1];
llRet += vLeft[j - 1][nums[k] - 1] * (nums.size() - k - 1 - iRight);
}
}
return llRet;
};
int m_c;
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 充满正能量得对大家说 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 算法终将统治宇宙,而我们统治算法。《喜缺全书》 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开
发环境: VS2022 C++17

相关文章:

C++前缀和算法的应用:统计上升四元组
C前缀和算法的应用:统计上升四元组 本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 题目 给你一个长度为 n 下标从 0 开始的整数数组 nums ,它包含 1 到 n 的所有数字,请你返回上…...

华泰证券:新奥能源:零售气待恢复,泛能与智家仍是亮点
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,由于新奥能源(02688)发布三季度经营数据: 1-3Q23:天然气零售量yoy-4.7%,燃气批发量yoy17.6%,综合能源销量yoy34.2%ÿ…...
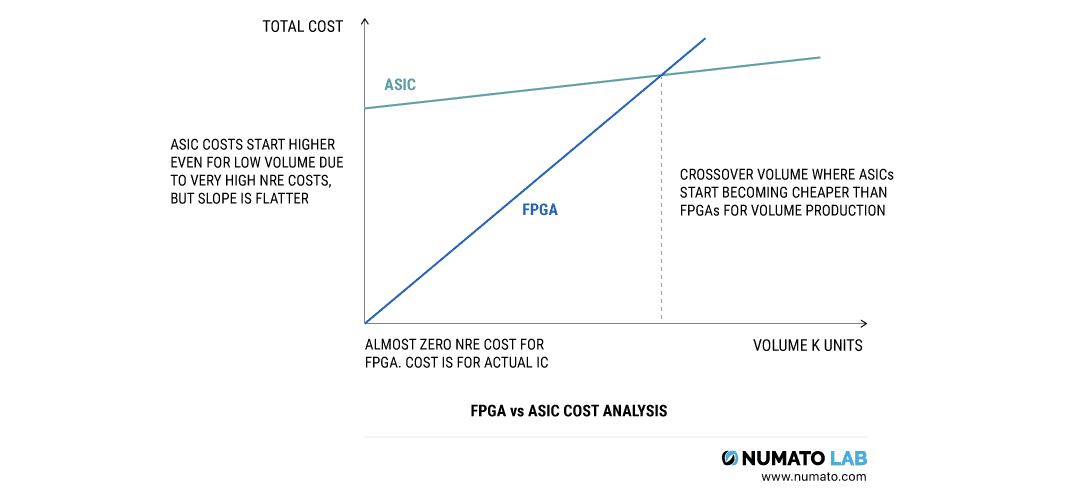
FPGA与ASIC有什么差异?二者该如何选用?
前言 对于一个数字电路的新手来说,这可能是会经常遇到的一个问题:FPGA和ASIC之间的区别是什么? 接下来本文将尝试讲解 “什么是FPGA?” 和 “什么是ASIC?”,然后讲述一些关于FPGA和ASIC的问题,例如它们之间…...

Kotlin run 用法
Kotlin 中的 .run 函数可以用于不同的场景,下面是一些常见的用法: 执行代码块并返回结果: val result run {// 在这里编写一些代码逻辑// 返回最后一个表达式的结果"Hello, Kotlin" }println(result) // 输出:Hello, …...
iZotope RX 10(音频修复和增强工具)
iZotope RX 10是一款音频修复和增强软件,主要特点包括: 声音修复:iZotope RX 10可以去除不良噪音、杂音、吱吱声等,使音频变得更加清晰干净。音频增强:iZotope RX 10支持对音频进行音量调节、均衡器、压缩器、限制器等…...
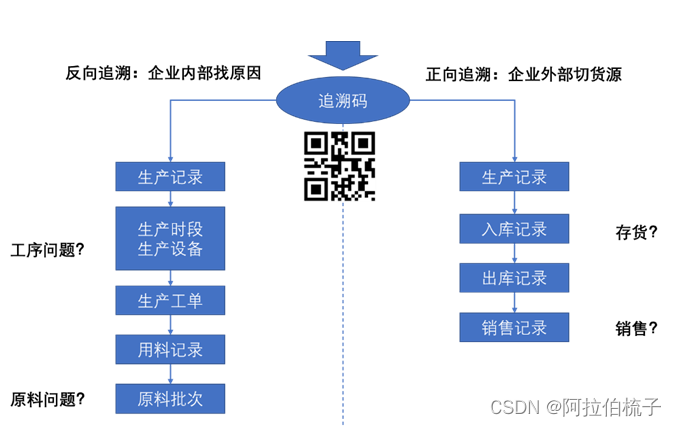
MES 价值点之数据追随
在现代制造业中,数据追溯已经越来越得到重视,特别是那些推行精益生产的企业重要性就更加突出了,而制造执行系统(MES)作为一种关键的生产管理工具,是能很好的为制造企业提供数据追溯功能。今天,和…...

yolo8制作自己的数据集训练和预测分割
一、训练coco128-seg数据集,增加一个类别 coco128-seg数据集下载: github链接 csdn链接 1、修改两个配置文件 (1)、修改"E:\python\ultralytics-main\ultralytics\cfg\datasets\coco128-seg.yaml"路径下的coco128-seg.yaml数据集配置文件,可以拷贝出来 修改数…...
分享一下怎么做一个同城配送小程序
如何制作一个同城配送小程序:功能特点、使用指南及未来展望 一、引言 随着互联网的快速发展,人们对于生活服务的需求越来越高。同城配送作为连接消费者与商家的桥梁,越来越受到人们的关注。本文将详细介绍如何制作一个同城配送小程序&#…...
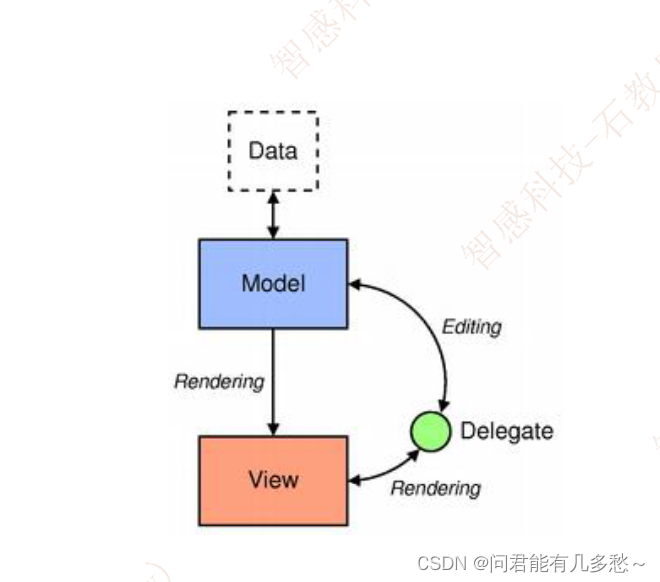
Qt 中model/View 架构 详解,以及案例实现相薄功能
model/View 架构 导读 我们的系统需要显示大量数据,比如从数据库中读取数据,以自己的方式显示在自己的应用程序的界面中。早期的 Qt 要实现这个功能,需要定义一个组件,在这个组件中保存一个数据对象,比如一个列表。我们对这个列表进行查找、插入等的操作,或者把修改…...

提高微星笔记本Linux下散热性能,MSI-EC 驱动新补丁发布
导读近日消息,今年早些时候,Linux 6.4 中添加了 MSI-EC 驱动程序,允许对 Linux 系统微星笔记本电脑进行更多控制。 MSI-EC 驱动程序近日迎来新补丁,为微星笔记本带来 Cooler Boost 功能。该功能允许提高笔记本电脑的风扇转速&…...

Apache Doris (五十): Doris表结构变更-动态分区(2)
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录...

AntDB数据库荣获 “2023年信创物联网优秀服务商”
日前,在2023世界数字经济大会暨第十三届智博会 2023京甬信创物联网产融对接会上,AntDB数据库再获殊荣,获评“2023年信创物联网优秀服务商”。 图1:2023年信创物联网优秀服务商颁奖现场 信创物联网是信息技术应用创新与物联网的结…...
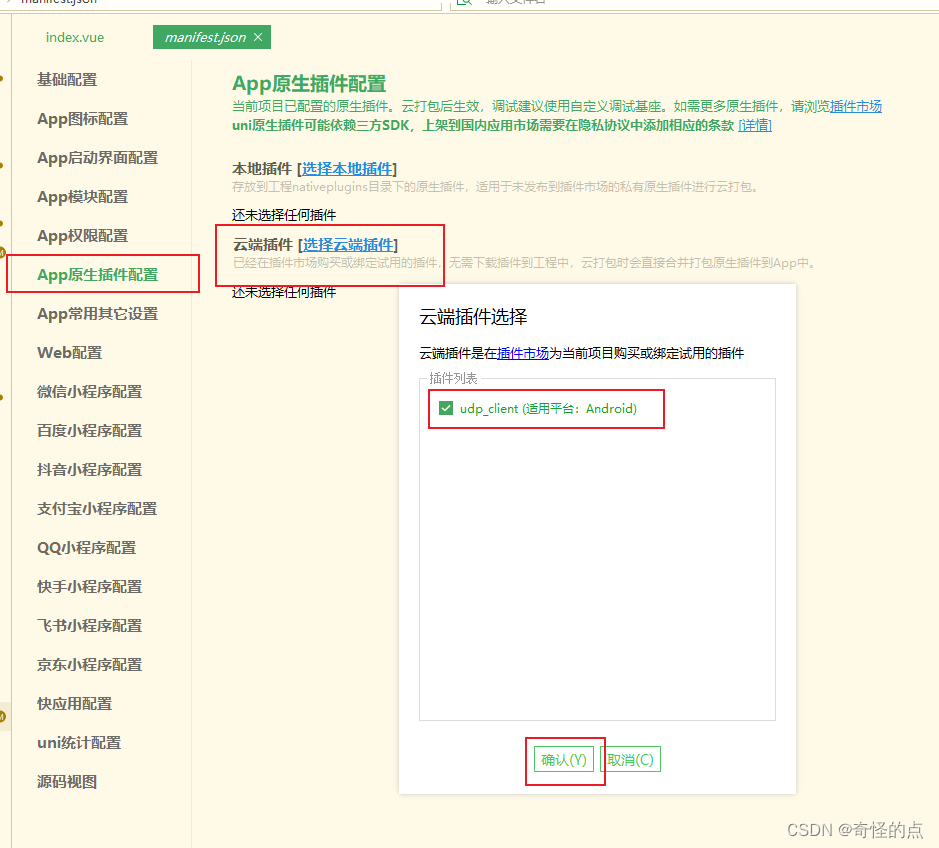
uniapp 使用 UDP
一、搭建UDP服务端,nodejs const dgram require("dgram");const message Buffer.from("你好,这是一个UDP广播消息"); const port 3000; // 用你想要的端口替换这里// 创建一个UDP套接字 const socket dgram.createSocket("…...
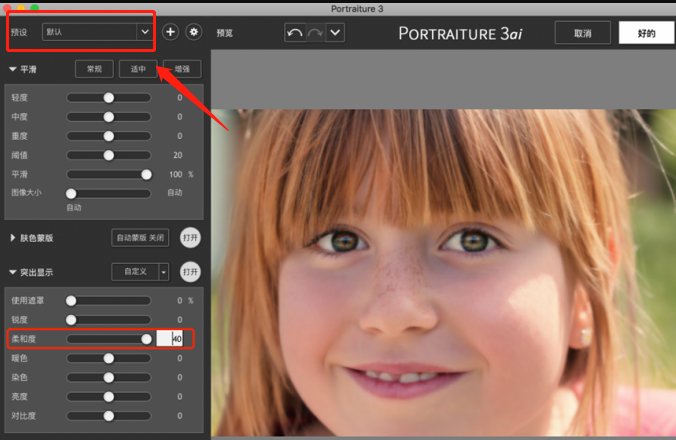
苹果相机怎么磨皮 苹果手机怎么磨皮
相信使用苹果相机的小伙伴都有这样的疑惑,苹果相机怎么磨皮?其实可以通过相机的参数进行设置从而达到磨皮的效果,如果觉得相机自带的设置磨皮效果不够好,可以下载磨皮软件来对照片磨皮。今天的文章就来给大家介绍苹果相机怎么磨皮…...

spring boot导入导出excel,集成EasyExcel
一、安装依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.2.0</version></dependency>二、新建导出工具类 <dependency><groupId>com.alibaba</groupId>&…...

【错误解决方案】ModuleNotFoundError: No module named ‘zarr‘
1. 错误提示 在python程序,尝试导入一个名为zarr的模块,但Python提示找不到这个模块。 错误提示:ModuleNotFoundError: No module named ‘zarr‘ 2. 解决方案 这可能是因为你尚未安装这个模块或者安装过程中出现了问题。 zarr是一个用于存…...

什么是集成测试?
什么是集成测试 集成测试(Integration Testing),也叫组装测试或联合测试。在单元测试的基础上,将所有模块按照设计要求(如根据结构图)组装成为子系统或系统,进行集成测试。 集成测试ÿ…...

Linux———— 运算命令
Shell与其他编程语言一样,支持多种类型的运算符,包括: 算术运算符:用于执行数学运算,例如加法、减法、乘法和除法。 关系运算符:用于比较两个值之间的关系,例如相等、大于、小于等。 布尔运算…...
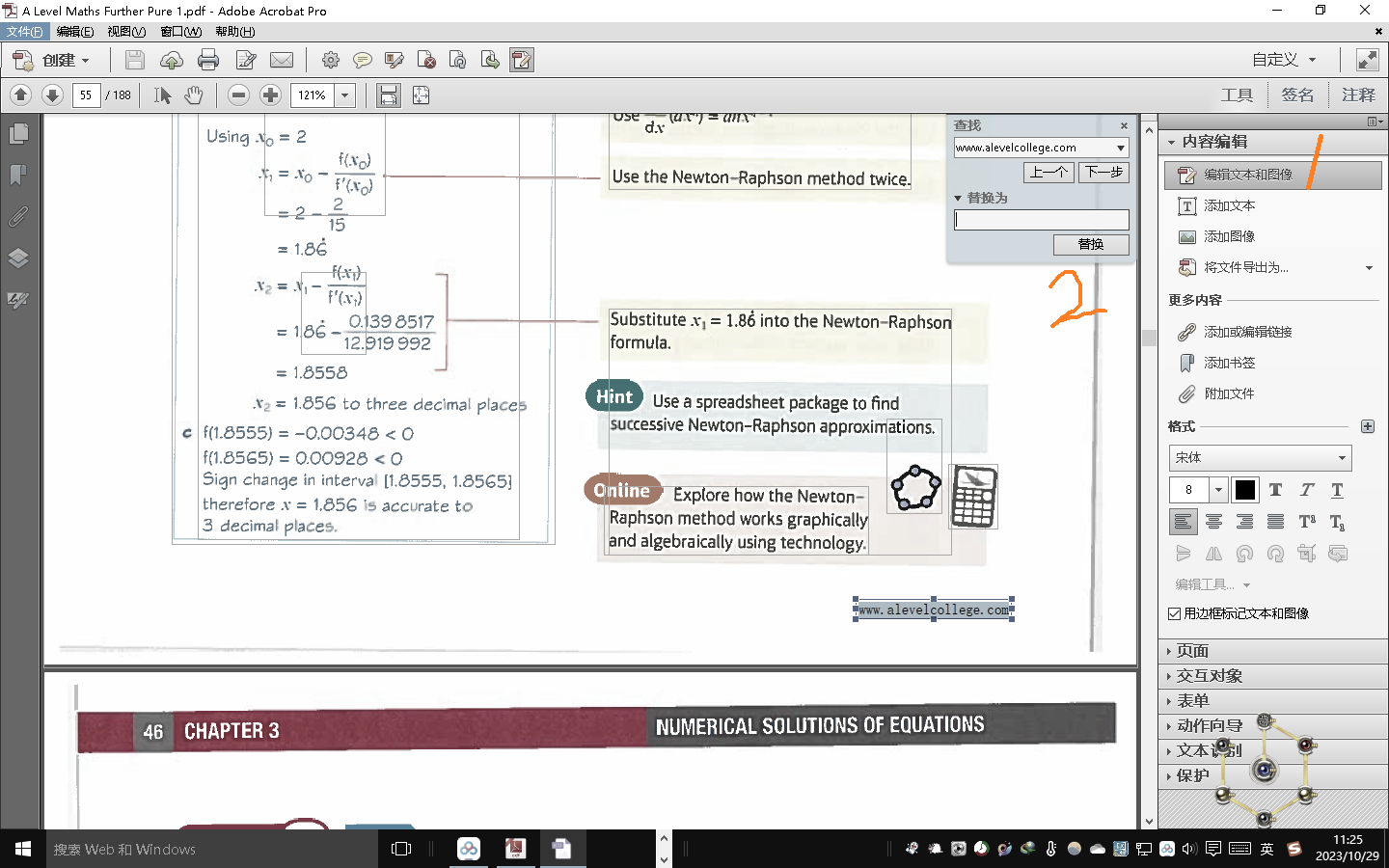
批量去除pdf每一页相同未知的同样的内容
例如我想去除每一页右下角的www.alevelcollege.com ①打开acrobat pro ②编辑文件和图像 ③ctrlF输入字符串www.alevelcollege.com替换为空 ④鼠标点击替换 ⑤回车键按下不放,会自动翻页,直到翻页到最后一页。...
HCIA数据通信——静态路由
之前的文章中我提到过静态路由: 数据通信——网络层(路由器以及数据转发流程)_路由器如何转发数据_咕噜跳的博客-CSDN博客这里只做一些简单描述。 路由器关注的是网络之间的通信。路由器以自身为中心,考虑的是如何将数据发送到目…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...
