Linux———— 运算命令
Shell与其他编程语言一样,支持多种类型的运算符,包括:
算术运算符:用于执行数学运算,例如加法、减法、乘法和除法。
关系运算符:用于比较两个值之间的关系,例如相等、大于、小于等。
布尔运算符: 用于执行逻辑运算,例如逻辑与、逻辑或、逻辑非。
字符串运算符:用于处理字符串,例如字符串连接、字符串相等性检查。
文件测试运算符: 用于检查文件属性,例如文件是否存在、文件是否可读等。
expr命令
expr (evaluate expressions 的缩写),译为“表达式求值”, `expr`是一种表达式计算工具,用于执行表达式求值操作。Shell expr 是一个功能强大,并且比较复杂的命令,它除了可以实现整数计算,还可以结合一些选项对字符串进行处理,例如计算字符串长度、字符串比较、字符串匹配、字符串提取等。
常用的算术运算符,假定变量 a 为 1,变量 b 为 2:
| 运算符 | 说明 | 举例 |
|---|---|---|
| + | 加法 | expr $a + $b 结果为 3 |
| - | 减法 | expr $a - $b 结果为 -1 |
| * | 乘法 | expr $a \* $b 结果为 2 |
| / | 除法 | expr $b / $a 结果为 2 |
| % | 取余 | expr $b % $a 结果为 0 |
| = | 赋值 | a=$b 将把变量 b 的值赋给 a |
注意:
- 表达式和运算符之间要有空格,例如 2+2 是不对的,必须写成 2 + 2,这与我们熟悉的大多数编程语言不一样。
- 完整的表达式要被 ` ` 包含,注意使用的是反引号 ` 而不是单引号 ',这个字符不是常用的单引号,在 Esc 键下边。
- 如果四则运算中如果使用了(),需要转义
\( 30+ 1 \)
求值表达式
算术运算符表达式(交互式)
expr 1 + 11 # 返回: 12
expr \( 30 + 10 \) \* 2 + 100 # 返回:180获取计算结果赋值给新变量语法
result=`expr 1 + 1` # 输出result得到结果: 2
2).echo+管道
字符串语法
| 语法 | 说明 | 示例 |
|---|---|---|
| expr length 字符串 | 计算字符串的长度 | expr length "helloworld" 返回: 10 |
| expr substr 字符串 start end | 截取字符串 | expr substr "helloworld" 1 2 返回: hestart 截取字符串的起始位置,从1开始end 截取字符串的结束位置,包含这个位置截取 |
| expr index 被查找字符串 需要查找的字符 | 获取第一个字符在字符串中出现的位置 | expr index "helloworld" l 返回: 3 |
| expr match 字符串 正则表达式expr 字符串 : 正则表达式 | 正则表达式匹配,返回值为符合匹配字符的长度,否则返回为0 "expr match" 命令用于匹配一个字符串中的部分文本,而正则表达式 ".*o" 的含义如下:
| expr match "helloworld" ".*o" 返回: 7 |
运行效果:
(())命令
双小括号(( )),用于进行数学运算表达式的执行 , 将数学运算表达式放在((和))之间。可以使用 获取(())表达式命令的结果,这和使用 获得变量值是一样的。
| 语法 | 说明 |
|---|---|
| ((a=64+6)) ((b=a-6)) ((c=a+b*2)) | 这种写法可以在计算完成后给变量赋值。以 ((b=a-6)) 为例,即将 a-6的运算结果赋值给变量 c。 注意,使用变量时不用加$前缀,(( )) 会自动解析变量名。 |
| a=$((1+6) b=$((a-1)) c=$((a+b*2)) | 可以在 (( )) 前面加上$符号获取 (( )) 命令的执行结果,也即获取整个表达式的值。以 c=$((a+b*2)) 为例,即将 a+b 这个表达式的运算结果赋值给变量 c。 注意,如果 c=((a+b)) 这样的写法是错误的,不加$就不能取得表达式的结果。 |
| ((a>7 && b==c)) | (( )) 也可以进行逻辑运算,在 if 语句中常会使用逻辑运算。 |
| echo $((a+10)) | 需要立即输出表达式的运算结果时,可以在 (( )) 前面加$符号。 |
| ((a=3+5, b=a+10)) | 对多个表达式同时进行计算, 多表表达式使用”,”号隔开 |
注意: 符号之间有无空格都可以 , (( a = 1 + 6 )) 等价于 ((a=1+6))
示例:ce.sh脚本代码
#!/bin/bash
# 计算1+6赋值给变量a
((a=1+6))# 计算变量a-1赋值给变量b
((b=a-1))# 计算变量a+变量b赋值给变量c
((c=a+b))# 打印变量a,变量b, 变量c的值
echo "a=${a},b=${b},c=${c}"# $赋值写法
a=$((1+6)) b=$((a-1)) c=$((a+b))
echo "a=${a},b=${b},c=${c}"# (())多个表达式计算赋值
((a=1+6,b=a-1,c=a+b))
echo "a=${a},b=${b},c=${c}"# echo输出直接使用(())
echo "1+6=$((1+6))"# (()) 用于逻辑表达式 在if中使用
if ((a>7 && b==c))
thenecho "a>7 && b==c 成立"
elseecho "a>7 && b==c 不成立"
fi运行效果:

总结:
- 括号内赋值: ((变量名=整数表达式))
- 括号外赋值: 变量名=$((整数表达式))
- 多表达式赋值: ((变量名1=整数表达式1,变量名2=整数表达式2,…))
- 与if条件句配合使用: if ((整数表达式))
let命令
let 命令和双小括号 (( )) 在数字计算方面功能一样。但是没有(())功能强大,let只能用于赋值计算,不能直接输出,不可以条件判断一起使用。let主要用于赋值,是最简洁的整数运算赋值命令。
let 赋值表达式
# 计算赋值用法: let 变量名=整数运算表达式
# 多个表达式计算赋值用法: let 变量名1=整数运算表达式1 变量名2=整数运算表达式2 ...- 语法功能等价于
((表达式)) - 多个表达式之间使用空格,不是”
,“号 - 对于类似
let a+b这样的写法,Shell 虽然计算了 a+b 的值,但却将结果丢弃。如果echo let a+b会直接输出字符串a+b;若不想这样,可以使用let sum=a+b将 a+b 的结果保存在变量 sum 中。
$[]命令
在Linux和Unix Shell中,`$[]` 是一种旧的、过时的方法用于执行数学运算。它可以用来计算表达式的值。例如,您可以使用 `$[]` 来执行基本的算术运算,如加法、减法、乘法和除法。

效果展示:

四种计算命令对比
| 命令 | 优点 | 缺点 |
|---|---|---|
| expr | 可以直接输出。 | 计算表达式里面引用变量使用$,特殊字符需要转义,只能计算一个表达式。 |
| (( )) | 直接输出,里面直接使用变量名,特殊字符不需要转义,多个表达式赋值。(直接求值输出推荐方式) | 需要获取值以后才可以输出。 |
| let | 赋值简单,特殊字符不需要转义。(赋值推荐方式) | 不能直接输出。 |
| $[ ] | 特殊字符不需要转义。 | 不能多表达式计算。 |
bc命令
Bash Shell内置了对整数运算的支持,但是并不支持浮点运算,而 linux bc (basic calculator)命令可以很方便的进行浮点运算。bc命令是Linux简单的计算器,能进行进制转换与计算。能转换的进制包括十六进制、十进制、八进制、二进制等。可以使用的运算符号包括(+)加法、(-)减法、(*)乘法、(/)除法、(^)指数、(%)余数等。
bc [options] [参数]选项options:
| 选项 | 说明 |
|---|---|
| -h | help,帮助信息 |
| -v | version,显示命令版本信息 |
| -l | mathlib, 使用标准数学库,例如使用内置函数就需要必须使用这个参数 |
| -i | interactive,强制交互 |
| -w | warn,显示 POSIX 的警告信息 |
| -s | standard,使用 POSIX 标准来处理 |
| -q | quiet,不显示欢迎信息 |
注意:
默认使用bc命令后回车会有很多欢迎信息, 可以使用
bc -q回车后不会有欢迎信息bc命令交互式下,输入quit 即可回到当前目录
bc需要每个表达式单独一行,并且要在运算符周围使用空格
参数:指定包含计算任务的文件。
常见的内置函数:
| 函数名 | 作用 |
| s(x) | 计算x的正弦值,x是弧度值 |
| c(x) | 计算x的余弦值,x是弧度值 |
| a(x) | 计算x的正切值,返回弧度值 |
| l(x) | 计算x的自然对数 |
| e(x) | 求e的x次方 |
| j(n,x) | 计算从n到x的阶数 |
测试效果: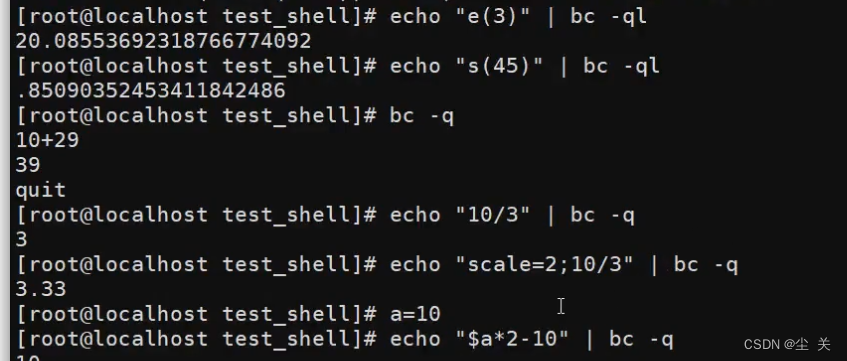
文件可以执行多条语句:

相关文章:

Linux———— 运算命令
Shell与其他编程语言一样,支持多种类型的运算符,包括: 算术运算符:用于执行数学运算,例如加法、减法、乘法和除法。 关系运算符:用于比较两个值之间的关系,例如相等、大于、小于等。 布尔运算…...
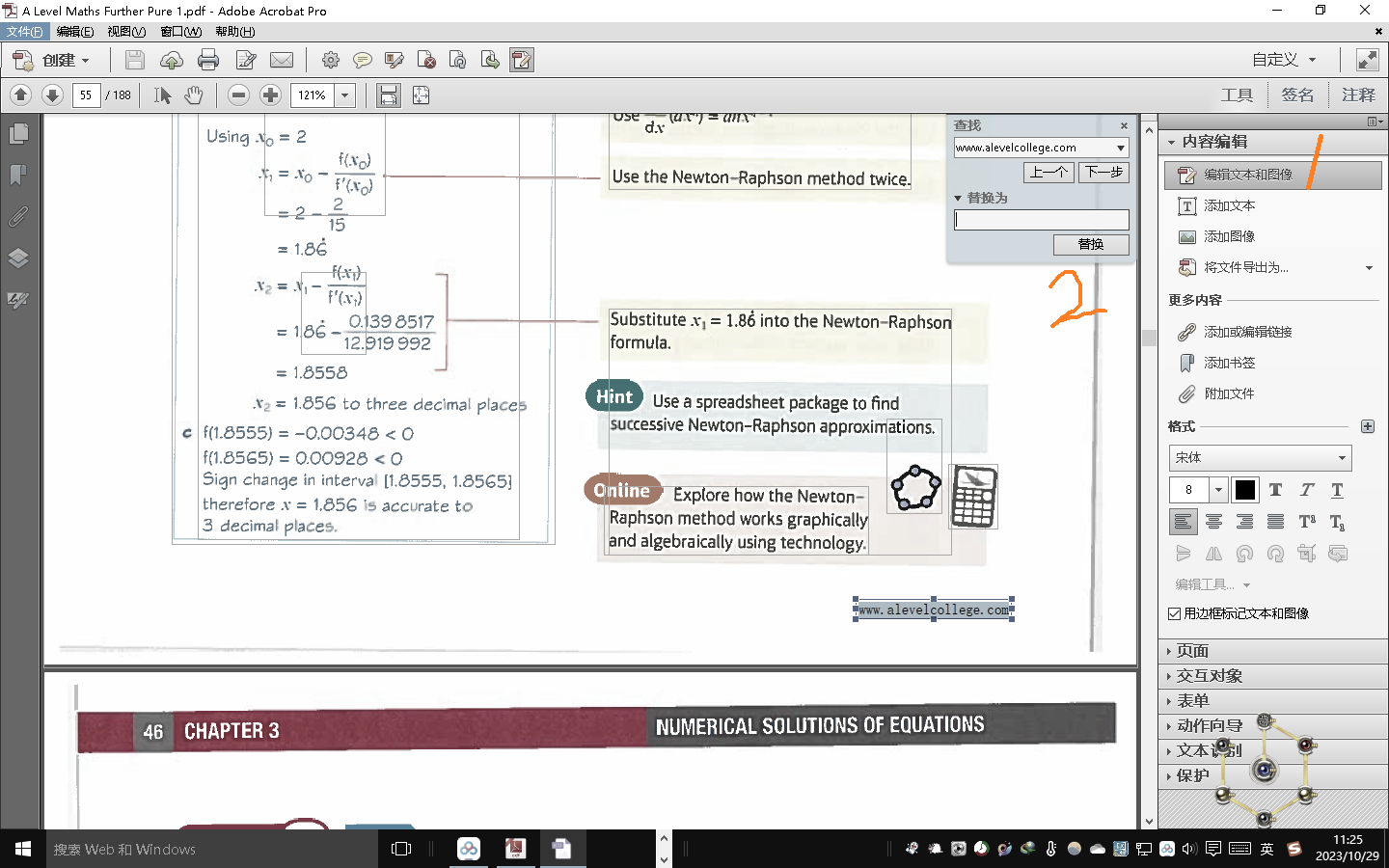
批量去除pdf每一页相同未知的同样的内容
例如我想去除每一页右下角的www.alevelcollege.com ①打开acrobat pro ②编辑文件和图像 ③ctrlF输入字符串www.alevelcollege.com替换为空 ④鼠标点击替换 ⑤回车键按下不放,会自动翻页,直到翻页到最后一页。...
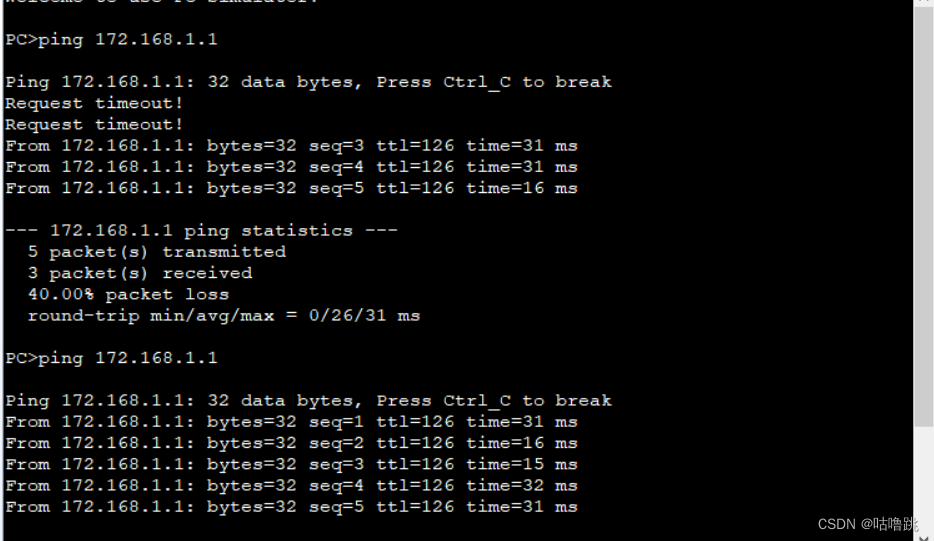
HCIA数据通信——静态路由
之前的文章中我提到过静态路由: 数据通信——网络层(路由器以及数据转发流程)_路由器如何转发数据_咕噜跳的博客-CSDN博客这里只做一些简单描述。 路由器关注的是网络之间的通信。路由器以自身为中心,考虑的是如何将数据发送到目…...
Fourier分析导论——第2章——Fourier级数的基本属性(E.M. Stein R. Shakarchi)
第 2 章 Fourier级数的基本属性(Basic Properties of Fourier Series) Nearly fifty years had passed without any progress on the question of analytic representation of an arbitrary function, when an assertion of Fourier threw new light on the subject. Thus…...
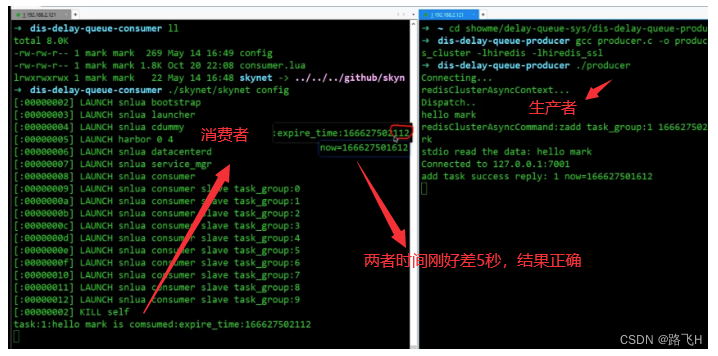
redis实现分布式延时队列
文章目录 延时队列简介应用场景案例:考虑:实现:整体思路:具体实现生产者消费者 运行结果 redis分布式延时队列优势redis分布式延时队列劣势 延时队列简介 延时队列是一种特殊的消息队列,它允许将消息在一定的延迟时间…...
Spring AOP源码解读
今天我们来分析Spring中AOP的源码,主要是关于SpringAOP是如何发挥作用的。 前期准备 首先我们需要有一个Spring AOP项目,添加好了SpringAOP的依赖。 <dependency><groupId>org.springframework</groupId><artifactId>spring-co…...

JavaScript基础入门01
目录 1.初识 JavaScript 1.1JavaScript 是什么 1.2发展历史 1.3JavaScript 和 HTML 和 CSS 之间的关系 2.JavaScript 的组成 3.前置知识 3.1第一个程序 4.JavaScript 的书写形式 4.1 行内式 4.2. 内嵌式 4.3.外部式 5.注释 6.输入输出 6.1输入: prompt 6.2输出: …...
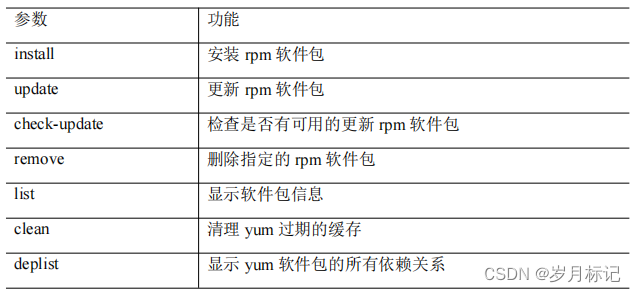
yum 命令
基本语法 yum [选项] [参数] 选项说明 -y 对所有提问都回答“yes” 参数说明 实操 yum list | grep firefox yum -y remove firefox yum -y install firefox...
Nginx 部署多个安全域名,多个服务【工作记录】
以下是本人通过Docker 部署的Nginx挂载出来的文件目录 先看下 nginx.conf 配置文件内容:如下 ps:当前文件就是安装后的初始内容,无修改。主要关注最后一行 include /etc/nginx/conf.d/*.conf;表示引入其他目录下的.conf配置文件;…...

性能测试QPS+TPS+事务基础知识分析
本篇文章是性能测试基础篇,主要介绍了性能测试中对QPSTPS事务的基础知识分析,有需要的朋友可以借鉴参考下,希望可以对广大读者有所帮助 事务 就是用户某一步或几步操作的集合。不过,我们要保证它有一个完整意义。比如用户对某一…...
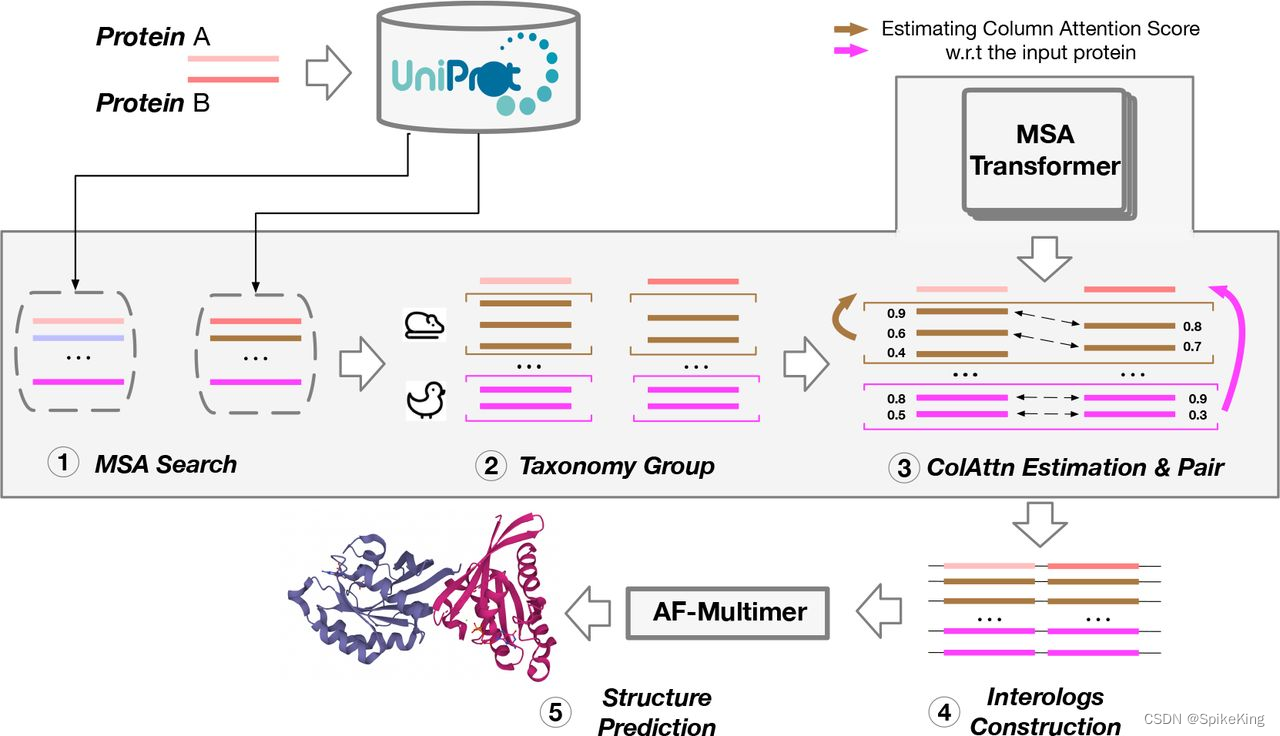
PSP - 蛋白质复合物 AlphaFold2 Multimer MSA Pairing 逻辑与优化
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/134144591 在蛋白质复合物结构预测中,当序列 (Sequence) 是异源多链时,无论是AB,还是AABB,都需要 …...

C++中vec.size()-1的坑
问题描述:如下代码, #include <iostream> #include <vector>using namespace std;int main() {vector<int> vec {};for (int i 0; i < vec.size() - 1; i) {cout << "i " << i << ", vec[i] …...

Flask Shell 操作 SQLite
一、前言 这段时间在玩Flask Web,发现用Flask Shell去操作SQLite还是比较方便的。今天简单地介绍一下。 二、SQLite SQLite是一种嵌入式数据库,它的数据库就是一个文件,处理速度快,经常被集成在各种应用程序中,在IO…...
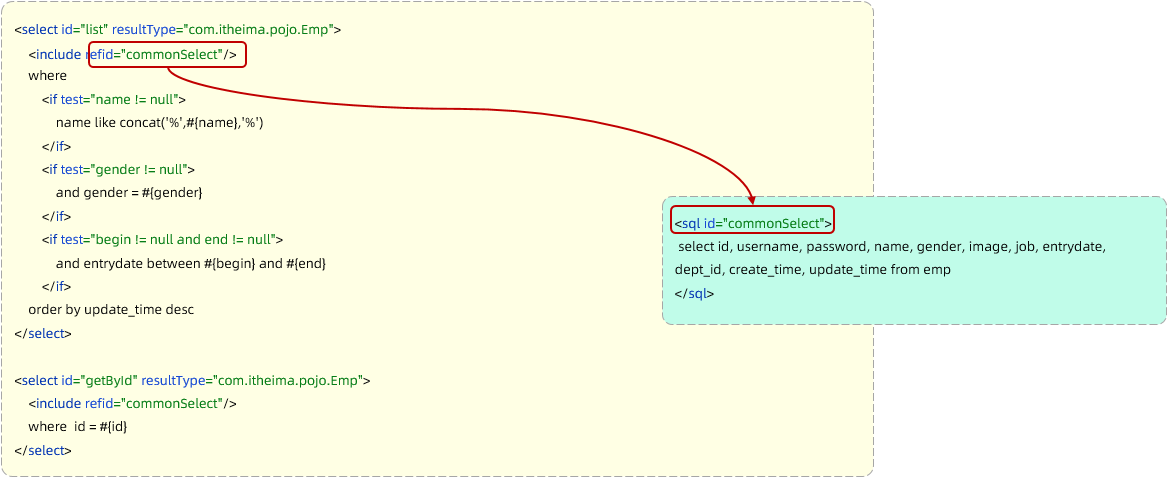
Mybatis—XML配置文件、动态SQL
学习完Mybatis的基本操作之后,继续学习Mybatis—XML配置文件、动态SQL。 目录 Mybatis的XML配置文件XML配置文件规范XML配置文件实现MybatisX的使用 Mybatis动态SQL动态SQL-if条件查询 \<if\>与\<where\>更新员工 \<set\>小结 动态SQL-\<forea…...
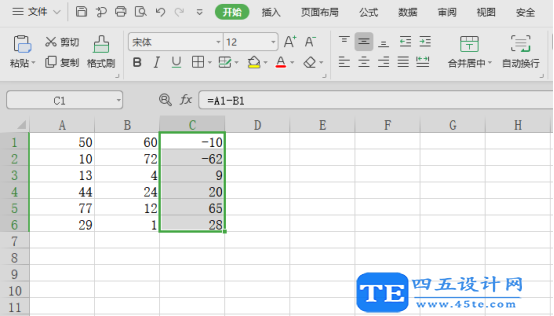
excel求差公式怎么使用?
利用excel求差,可能有许多的小伙伴已经会了,不过还是存在一些不太熟悉的朋友们,所以这里有必要讲解一下。其实求差的实现主要就是一个公式,就是用一个单元格中的数字“减去”另一个单元格中的数字“等于”第三个单元格。此公式掌握…...

高效分割分段视频:提升您的视频剪辑能力
在数字媒体时代,视频剪辑已经成为一项重要的技能。无论是制作个人影片、广告还是其他类型的视频内容,掌握高效的视频剪辑技巧都是必不可少的。本文将介绍如何引用云炫AI智剪高效地分割和分段视频,以提升您的视频剪辑能力。以下是详细的操作步…...
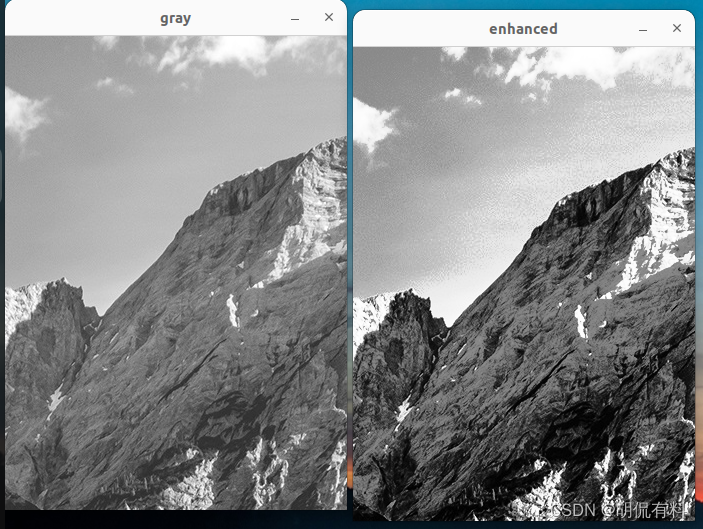
【c++|opencv】二、灰度变换和空间滤波---2.直方图和均衡化
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 图像直方图、直方图均衡化 1. 图像直方图 #include <iostream> #include <opencv2/opencv.hpp>using namespace cv; using namespace std;…...
)
【Windows】线程同步之信号量(Semaphores)
概述: semaphores 的说明和使用 微软官方文档: Semaphore Objects - Win32 apps | Microsoft Learn Semaphores是解决各种 producer/consumer问题的关键要素。这种问题会存有一个缓冲区,可能在同一时间内被读出数据或被写入数据。 理论可以证…...
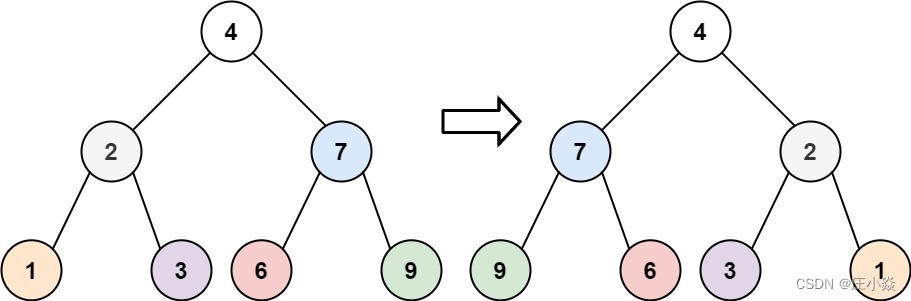
二叉树问题——前中后遍历数组构建二叉树
摘要 利用二叉树的前序,中序,后序,有序数组来构建相关二叉树的问题。 一、构建二叉树题目 105. 从前序与中序遍历序列构造二叉树 106. 从中序与后序遍历序列构造二叉树 889. 根据前序和后序遍历构造二叉树 617. 合并二叉树 226. 翻转二…...
)
Java保留n位小数的方法(超简洁)
要输出double类型保留n位小数的几种方法如下: 我们以保留6位小数为例 方法一:使用DecimalFormat类 import java.text.DecimalFormat;public class Main {public static void main(String[] args) {double number 3.141592653589793;DecimalFormat df …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
