C++基础算法④——排序算法(快速、归并附完整代码)
快速排序
快速排序是对冒泡排序的一种改进。
它的基本思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行快速排序,以达到整个序列有序。
假设我们现在对 6 1 2 7 9 3 4 5 1 0 8 这个10个数进行排序。
int main(){int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];qsort(1,n);for(int i=1;i <=n;i++){cout<<a[i]<<" ";} return 0;
}
首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数)。为了方便,就让第一个数6作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在6的右边,比基准数小的数放在6的左边,类似下面这种排列:
int a[10001];
void qsort(int l,int r){int i,j,mid;i=l+1,j=r;mid=a[l];
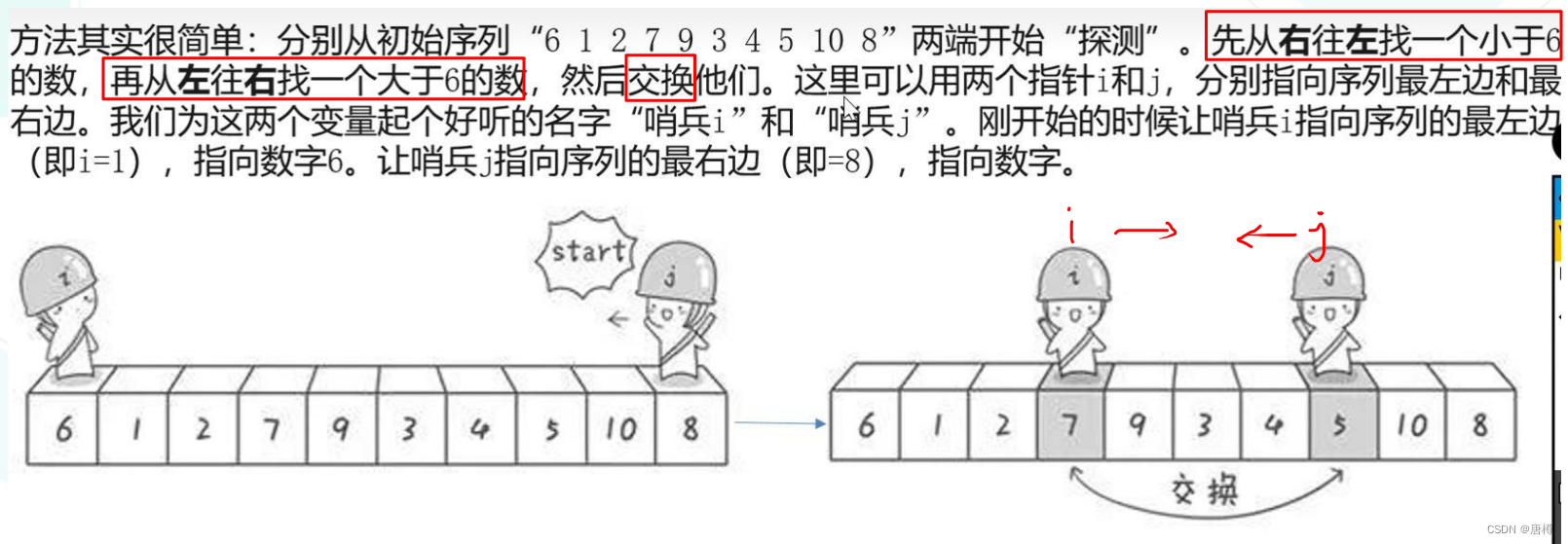
可以发现,i从第二个位置开始,j从最后一个位置开始;当 i 指向的值 大于基准值6 而且 当 j 指向的值 小于基准值6,就把这两个值交换,然后接着往下继续比。
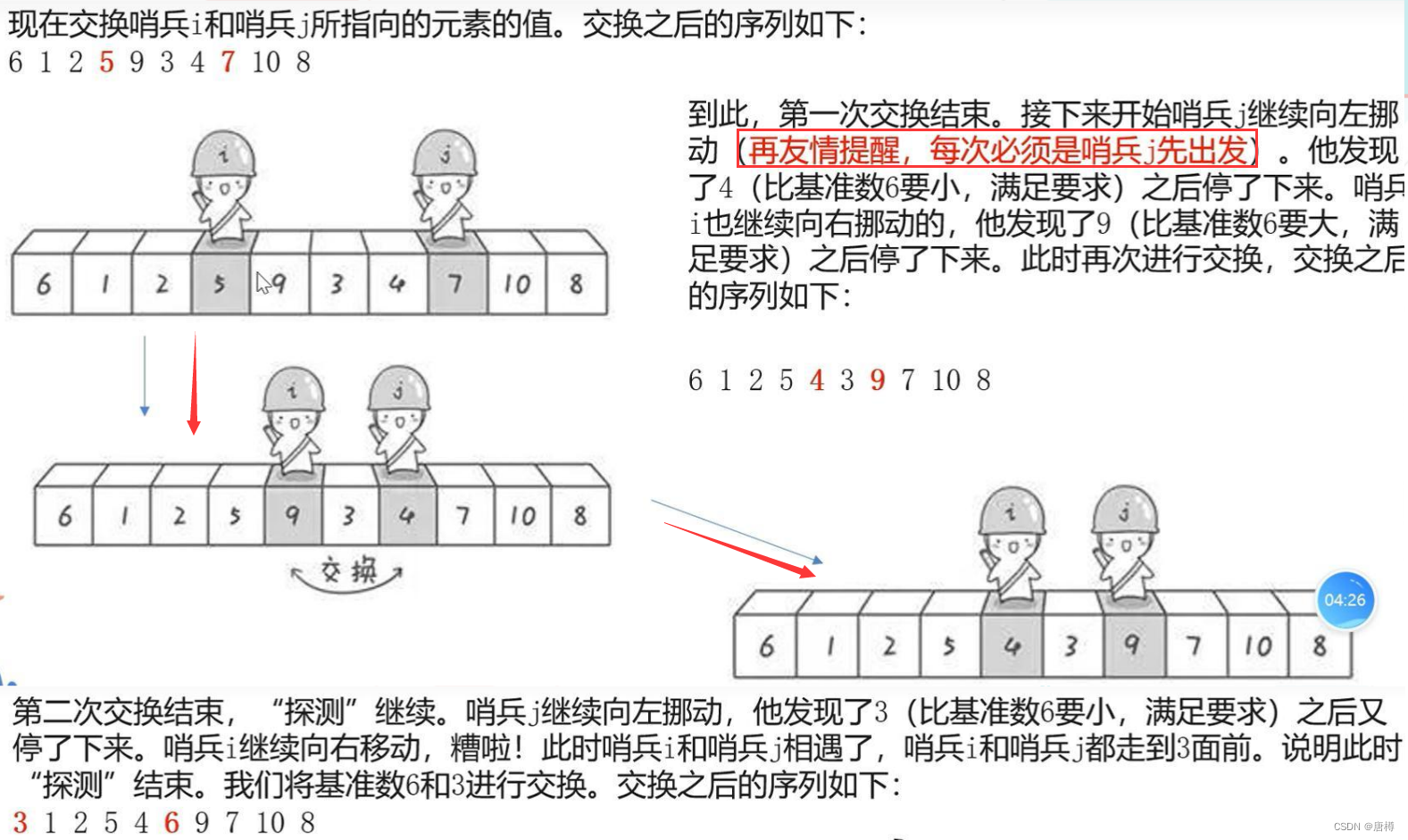
while(i<=j){ //当 i j 没有碰到while(a[i]<mid) i++;while(a[j]>mid) j--;if(i<=j){swap(a[i],a[j]);i++; j--;}}
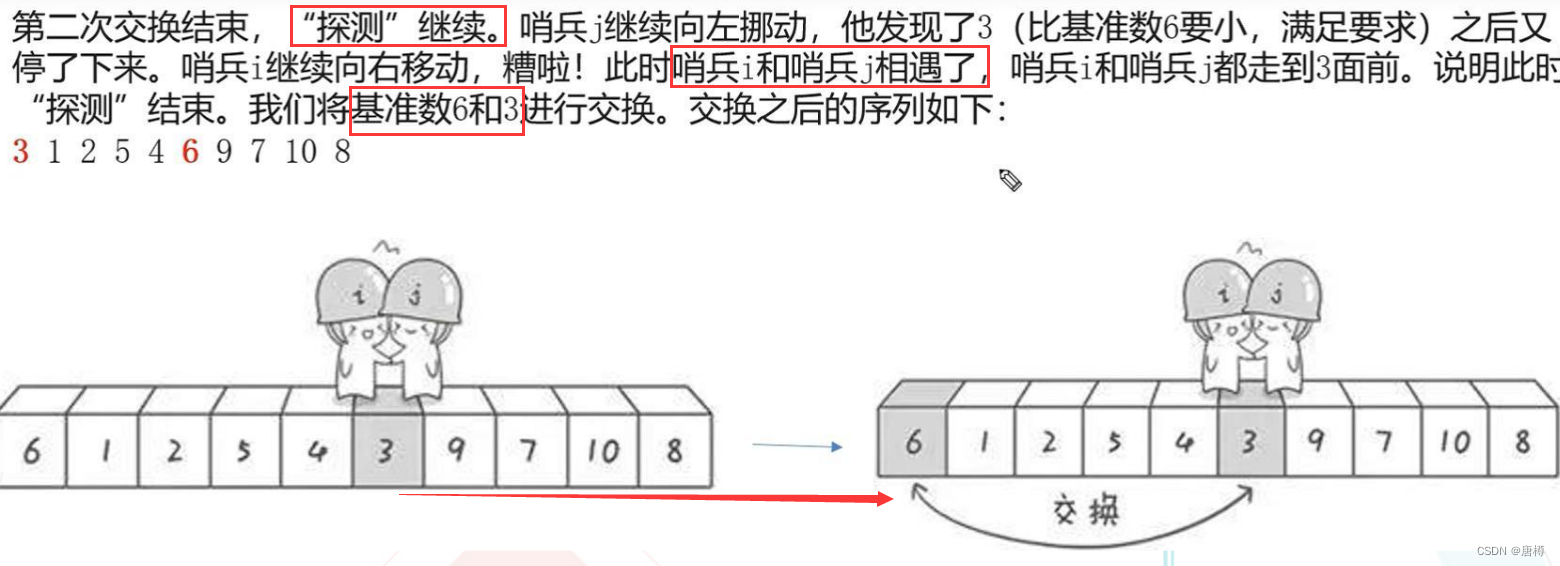
当 i j 相遇了,就把 j指向的值 与基准数交换。
swap(a[j],a[l]); //交换基准数
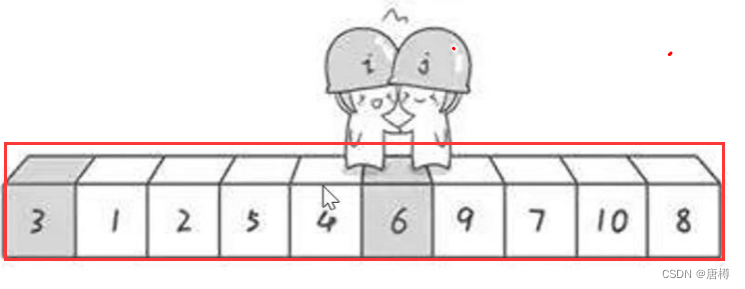
可以发现,一趟完毕,原基准数6的左边值一定比6小,右边比6大。这样就确定了基准数6的排序。
接下来,对于6左边的序列3 1 2 5 4和右边的序列9 7 10 8分别进行快速排序。
把整体分了左右边,再把左边的序列3 1 2 5 4看成新的重新进行快速排序。不断地分解。
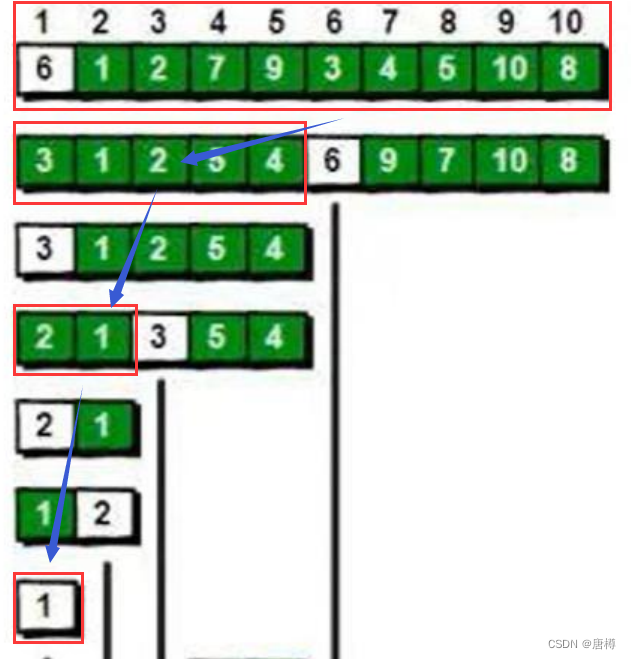
所以这个排序运用了分治的思想!
完整代码:
#include<bits/stdc++.h>
using namespace std;
int a[10001];
void qsort(int l,int r){int i,j,mid;i=l+1,j=r;mid=a[l];while(i<=j){while(a[i]<mid) i++;while(a[j]>mid) j--;if(i<=j){swap(a[i],a[j]);i++; j--;}}swap(a[j],a[l]); //交换基准数if(l<j) qsort(l,j-1);if(i<r) qsort(i,r);
}
int main(){int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];qsort(1,n);for(int i=1;i <=n;i++){cout<<a[i]<<" ";} return 0;
}快速排序是不稳定的排序方法,时间复杂度是O(nlog2n),速度快,平均时间来说,快速排序是最好的一种内部排序方法。但快速排序需要一个栈空间实现递归,每一趟排序都会将记录序列分割成两个子序列,栈最大深度为log(n+1)。
归并排序
归并的思路(分治)是把一个大问题a拆解成两个小问题b和c,解决了两个子问题再整合一下,就解决了原问题。用递归的方法,先分解再合并(分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突)。
- 稳定性:稳定;
- 空间复杂度O(n);
- 复杂度:时间复杂度O(nlogn);
- 优缺点:效率高且稳定,但是消耗的辅助空间与原数据空间成正比。
int main(){cin>>n;for(int i=1;i<=n;i++){ //输入 cin>>a[i];}//归并排序mergesort(1,n);for(int i=1;i<=n;i++){ //输出 cout<<a[i]<<" ";}return 0;
}
- 递归分解
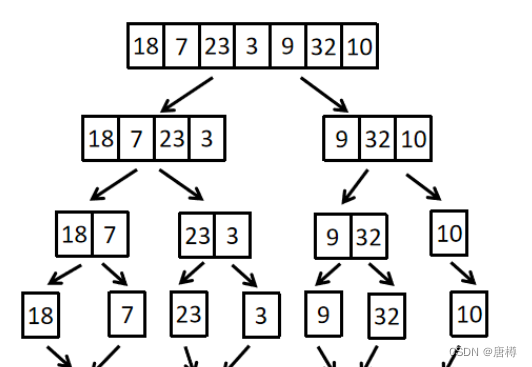
不断地二分分解,拆左右。
void mergesort(int l,int r){int mid = (l+r)/2;if(l==r) return ;mergesort(l,mid); //左边排序mergesort(mid+1,r);//右边排序//上面已经拆成一个一个 merge(l,mid,mid+1,r); //合并操作
}
分解到1个值,然后再合并排序。合并的思路看成:左边是有序的a数组;右边是有序的b数组。两数组开始比较,小的值依次存到c数组。
int a[100],c[100],n,cnt;
void merge(int left,int i,int j,int right){int lenc = left;int len1 = left; //左边开头 看成a[] int len2 = j; //右边开头 看成b[] while(len1<=i && len2<=right){ //并c[] if(a[len1]<a[len2]){ //左边小于右边 c[lenc++] = a[len1++];}else{//右边小于左边c[lenc++] = a[len2++];}} while(len1<=i){c[lenc++] = a[len1++];} while(len2<=right){c[lenc++] = a[len2++];}//把排好序的c数组存回a数组里面for(int k=left;k<=right;k++){a[k]=c[k];}
}
完整代码:
#include<bits/stdc++.h>
using namespace std;
int a[100],c[100],n,cnt;
void merge(int left,int i,int j,int right){int lenc = left;int len1 = left; //左边开头 看成a[] int len2 = j; //右边开头 看成b[] while(len1<=i && len2<=right){ //并c[] if(a[len1]<a[len2]){ //左边小于右边 c[lenc++] = a[len1++];}else{//右边小于左边c[lenc++] = a[len2++];}} while(len1<=i){c[lenc++] = a[len1++];} while(len2<=right){c[lenc++] = a[len2++];}//把排好序的c数组存回a数组里面for(int k=left;k<=right;k++){a[k]=c[k];}
} void mergesort(int l,int r){int mid = (l+r)/2;if(l==r) return ;mergesort(l,mid); //左边排序mergesort(mid+1,r);//右边排序//上面已经拆成一个一个 merge(l,mid,mid+1,r); //合并操作
}
int main(){cin>>n;for(int i=1;i<=n;i++){ //输入 cin>>a[i];}//归并排序mergesort(1,n);for(int i=1;i<=n;i++){ //输出 cout<<a[i]<<" ";}return 0;
}相关文章:

C++基础算法④——排序算法(快速、归并附完整代码)
快速排序 快速排序是对冒泡排序的一种改进。 它的基本思想是:通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行快速排序,以达到整个序列有序。 假设我们现在对 …...

高防CDN如何在防护cc上大显神通
高级防御CDN(Content Delivery Network)在对抗CC(HTTP Flood)攻击方面扮演着关键的角色,具备以下重要职能和作用: 流量分散:CC攻击的目标是通过大规模的HTTP请求使服务器过载,从而导…...

解决CSS中height:100%失效的问题
出现BUG的场景,点击退出到登录页面,发现高度不对 上面出现了一种只是占了内容的高度,没有占满100%,为什么会出现这种情况呐? 让div的height"100%",执行网页时,css先执行到࿰…...

小红书穿搭类种草营销怎么做?纯干货
在众多营销方式中,穿搭类种草营销以其独特的优势在小红书平台上崭露头角。穿搭类种草营销,以其独特的优势,成为了品牌和商家推广产品的重要方式。其优势主要体现在以下几个方面: 1. 高度相关性:小红书平台的用户主要是…...

什么是ARFF文件,以.arff结尾
关于arff,主要涉及三个输入类:概念、实例和属性。 1.概念简单而言就是需要被处理的东西, 2. 实例这个词有些陌生,但是可以大致认为其为样本, 3. 属性就是数据表中的一列。 为什么要用arff?(arff介绍&#x…...

华为OD机考算法题:计算疫情扩散时间
题目部分 题目计算疫情扩散时间难度难题目说明在一个地图中(地图由 n * n 个区域组成)有部分区域被感染病菌感染区域每天都会把周围(上下左右)的4个区域感染。 请根据给定的地图计算多少天以后,全部区域都会被感染。 如果初始地图上所有区域全部都被感染࿰…...
29岁从事功能测试5年被辞,面试4个月还没到工作......
最近一个32岁的老同学因为被公司辞退,聊天过程中找我倾诉,所以写下了这篇文章。 他是15年二本毕业,学的园林专业,人属于比较懒的那种,不爱学习,专业学的也一般。实习期间通过校招找到了一份对口的工作。但…...

再记【fatal error C1001: 内部编译器错误】的一个原因
平台:Windows 11、Visual Studio 2022 报错信息 已启动生成... 1>------ 已启动生成: 项目: PointMatchingModel, 配置: Debug x64 ------ 1>PointMatchingModel.cpp 1>C:\tools\vcpkg\installed\x64-windows\include\pcl\registration\impl\ia_fpcs.hpp…...

数据分析、大数据分析和人工智能之间的区别
数据分析、大数据分析和人工智能近年来十分热门,三者之间看起来有相似之处,也有不同之处。今天就来谈谈三者间的区别。 数据分析 数据分析是指对数据进行分析,从中提取有价值的信息,以支持企业或组织的决策制定。数据分析可以针对…...
Spring系列之基础
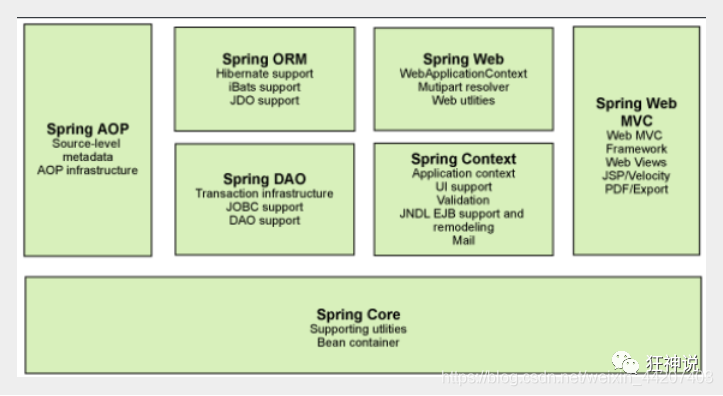
目录 Spring概述 Spring的优点 Spring Framework的组成 总结 Spring概述 Spring 是目前主流的 Java Web 开发框架,是 Java 世界最为成功的框架。该框架是一个轻量级的开源框架,具有很高的凝聚力和吸引力。它以Ioc(控制反转)和…...
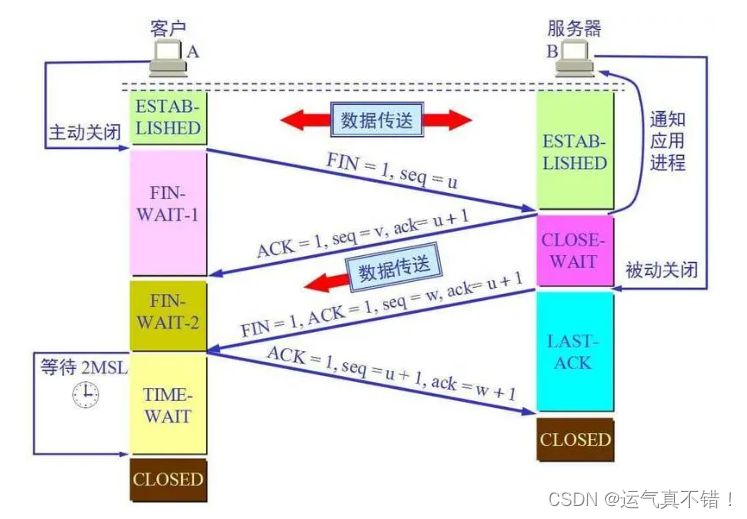
Android开发知识学习——TCP / IP 协议族
文章目录 学习资源来自:扔物线TCP / IP 协议族TCP连接TCP 连接的建立与关闭TCP 连接的建立为什么要三次握手? TCP 连接的关闭为什么要四次挥手? 为什么要⻓连接? 常见面试题课后题 学习资源来自:扔物线 TCP / IP 协议…...

思维训练 第四课 省略句
系列文章目录 文章目录 系列文章目录前言一、省略的十五种情况1.并列复合句中某些相同成分的省略2.在用when, while, if, as if, though, although, as ,until, whether等连词引导的状语从句中,如果谓语有be,而主语又跟主句的主语相同或是(从句主语是&am…...
soul协议算法
逆向工程技术是指对软件或应用程序进行逆向分析以了解其内部机制和功能的过程。虽然我无法详细介绍"Soul App"的逆向工程技术,但以下是一些常见的逆向工程技术,可能与你的研究相关: 1. 反汇编(Disassembly)…...

电子产品的认证体系
一、国内认证体系 1、CNAS认可:对认证机构的认可 CNAS全称是China National Accreditation Service for Conformity Assessment,中国合格评定国家认可委员会,由国家认证认可监督管理委员会(CNCA)批准设立并授权的唯一…...

大厂面试题-网络四元组
四元组,简单理解就是在TCP协议中,去确定一个客户端连接的组成要素,它包括源 IP地址、目标IP地址、源端口号、目标端口号。 正常情况下,我们对于网络通信的认识可能是这样(如图)。 服务端通过Server Socket建立一个对指定端口号…...

【通义千问“助力用户运营,无代码开发实现API连接广告推广和CRM】
通义千问:阿里云推出的超大规模语言模型 通义千问,是阿里云推出的一个超大规模的语言模型,功能包括多轮对话、文案创作、逻辑推理、多模态理解、多语言支持。这款产品的主要目标是帮助用户在无需编程的情况下,通过API连接广告推广…...
数据结构第一课-----------数据结构的介绍
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...
)
Python武器库开发-常用模块之OS模块(十一)
常用模块之OS模块(十一) Python中的 os 模块提供了非常丰富的方法用来处理文件和目录,可以执行一些操作系统的功能。常用的方法如下表所示: 序号方法描述1os.access(path, mode)检验权限模式2os.chdir(path)改变当前工作目录3os.chflags(path, flags)设…...

Vectrosity 插件使用
1 下载 https://download.csdn.net/download/moonlightpeng/88490704?spm1001.2014.3001.5503 2 使用,目前在2020.3.3上测试可以 导入时选5.6 再导入demo...

数据结构详细笔记——并查集
文章目录 逻辑结构存储结构并、查代码实现Union 操作的优化Find 操作的优化(压缩路径) 逻辑结构 集合:将各个元素划分为若干个互不相交的子集的集合 森林是m(m>0)棵互不相交的树的集合 存储结构 #define SIZE 13 int UFSets[SIZE]; …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
