【蓝桥杯集训·周赛】AcWing 第92场周赛
文章目录
- 第一题 AcWing 4864. 多边形
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第二题 AcWing 4865. 有效类型
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 第三题 AcWing 4866. 最大数量
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
第一题 AcWing 4864. 多边形
一、题目
1、原题链接
4864. 多边形
2、题目描述
如果一个正多边形的边数 n 能被 4 整除,那么就称该正多边形是美丽的。
现在,给定一个正多边形的边数 n,请你判断它是否是美丽的。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据占一行,包含一个整数 n。
输出格式
每组数据输出一行结果,如果给定正多边形是美丽的,则输出
YES,否则输出NO。数据范围
前 3 个测试点满足 1≤T≤10。
所有测试点满足 1≤T≤104,3≤n≤109。输入样例:
4 3 4 12 1000000000输出样例:
NO YES YES YES
二、解题报告
1、思路分析
(1)按照题意模拟即可,输出答案即为所求。
(2)注意YES与NO的大小写问题。
2、时间复杂度
时间复杂度为O(n)
3、代码详解
#include <iostream>
using namespace std;
int t;
int main(){cin>>t;while(t--){int n;cin>>n;if(n%4==0) cout<<"YES"<<endl;else cout<<"NO"<<endl; }return 0;
}
第二题 AcWing 4865. 有效类型
一、题目
1、原题链接
4865. 有效类型
2、题目描述
在本题中,关于有效类型字符串,具体定义如下:
int是有效类型字符串。- 如果字符串
X和字符串Y都是有效类型字符串,则pair<X,Y>是有效类型字符串。 现有一行若干个单词,每个单词要么是pair,要么是int,并且其中int的数量恰好为 n 个。你可以在不改变单词顺序的前提下,在这一行中任意添加
<、>、,符号。你的任务是 构造出一个有效类型字符串。
输出这个有效类型字符串。
注意:
有效类型字符串中不含空格或其它多余字符。 可以证明如果存在满足条件的有效类型字符串,那么它一定是唯一的。
如果不存在满足条件的有效类型字符串,输出Error occurred即可。输入格式
第一行包含整数 n,表示给定单词中
int的数量。第二行包含若干个单词,每个单词要么是
pair,要么是int。输出格式
输出满足条件的有效类型字符串,如果不存在,则输出
Error occurred。注意,有效类型字符串中不含空格或其它多余字符。
数据范围
前 6 个测试点满足:1≤n≤5。
所有测试点满足:1≤n≤105,输入的总单词数量不超过 105,输入的int数量恰好为 n。输入样例1:
3 pair pair int int int输出样例1:
pair<pair<int,int>,int>输入样例2:
1 pair int输出样例2:
Error occurred
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总:yyds
数据范围为105,时间复杂度控制在O(nlogn)
(1)可以发现每一个满足条件的有效类型字符串,都满足一个以pair为根结点int为左右儿子的二叉树。而且,每出现一个pair,必须有左右儿子;每出现一个int,必须没有左右儿子(即输入多组int是不合法的)。所以,只有满足每个根结点pair都有孩子,每个int都没有孩子,而且构造成的二叉树正好将所有的输入都用到(即不能多单词也不能少单词),就是满足条件类型的字符串。否则就不是有效类型字符串。而输入和输出便是二叉树的前序遍历。
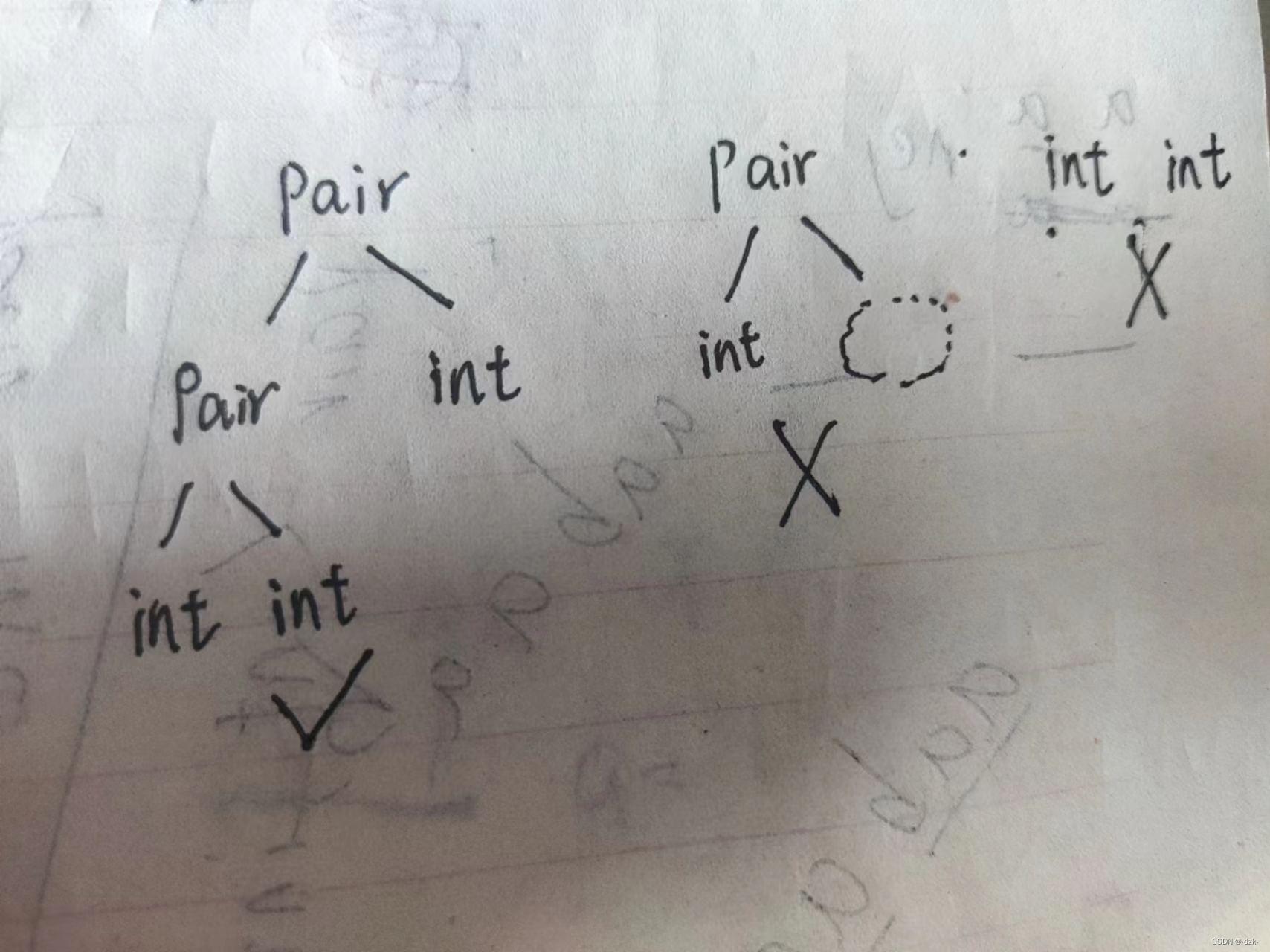
(2)我们可以通过上述规则,来判断给定的输入能否构造出上述的二叉树,如果可以,我们对二叉树的前序遍历进行输出(同时,每输出一个根结点pair,之后输出一个<,在遍历完左子树后输出一个,,遍历完右子树后输出一个>)。
(3)模拟上述过程,输出即为所求。
2、时间复杂度
时间复杂度为O(n)
3、代码详解
#include <iostream>
#include <string>
using namespace std;
string s,ans;
bool dfs(){if(cin>>s){ //每次调用dfs建树时,必须有输入,如果调用了但是没有输入,直接返回falseif(s=="pair"){ //如果输入pair需要递归建立左右子树ans+=s+'<';if(!dfs()) return false; //递归构建左子树ans+=',';if(!dfs()) return false; //递归构建右子树ans+='>';}else ans+=s; //如果输入int直接加到答案中即可}else return false;return true;
}
int main(){int n;cin>>n;bool flag=dfs();string tmp;if(!flag||cin>>tmp) cout<<"Error occurred"; //如果无法构成树(缺少输入或者输入出现多余),则不合法else cout<<ans; //正好用到所有输入的单词,而且可以按照规则构造成二叉树,按题目要求输出答案return 0;
}
第三题 AcWing 4866. 最大数量
一、题目
1、原题链接
4866. 最大数量
2、题目描述
一个无向图有 n 个点,编号 1∼n。
这些点之间没有任何边。
给定 d 个需求,编号 1∼d。
其中,第 i 个需求是让点 xi 和点 yi 连通。
需求可能存在重复。
在本题中,你需要依次解决 d 个问题,编号 1∼d。
其中,第 i 个问题是,请你在图中添加恰好 i 条无向边(不能添加重边和自环),使得:
- 前 i 个需求都得到满足。
- 所有点的度的最大值尽可能大。
对于每个问题,你不需要输出具体方案,你只需要 输出度的最大可能值。
注意:
如果点 a 和点 b 之间存在路径,则称点 a 和点 b 连通。 图中与点 a 关联的边数,称为点 a 的度。 d
个问题之间是相互独立的,每个问题的答案都必须独立计算。输入格式
第一行包含两个整数 n,d。
接下来 d 行,其中第 i 行包含两个整数 xi,yi,表示第 i 个需求是让点 xi 和点 yi 连通。
输出格式
共 d 行,其中第 i 行输出第 i 个问题中,度的最大可能值。
数据范围
前三个测试点满足,2≤n≤10。
所有测试点满足,2≤n≤1000,1≤d≤n−1,1≤xi,yi≤n,xi≠yi。输入样例1:
7 6 1 2 3 4 2 4 7 6 6 5 1 7输出样例1:
1 1 3 3 3 6输入样例2:
10 8 1 2 2 3 3 4 1 4 6 7 8 9 8 10 1 4输出样例2:
1 2 3 4 5 5 6 8
二、解题报告
1、思路分析
思路来源:4866. 最大数量
y总yyds
数据范围为1000,时间复杂度控制在O(n2)或O(n2logn)
(1)针对每个需求i让点xi和yi连通,即使xi和yi在一个集合中,也就是用到了并查集的合并操作。
(2)前i个操作总共可以使用i条边使每个点相连,而我们满足前i个需求,即让xi和yi连通,可能不会用完i条边。假设我们已经满足前i个需求后还剩余cnt条边,而前i个需求已经将所有元素合并成了某些集合(k1,k2,k3,...,kd),而这些集合中点度数最大为集合中元素数-1,即其中的某个点与其他所有点都相连。我们将剩余的边数连到某个集合中,不会改变该集合的最大度数。如果用边将两个集合相连,则合并后集合的度比合并前任意一个集合的度都要大(合并后集合的度也就是合并后集合的总元素数-1)。而总共可以合并cnt+1个集合,所以我们需要将元素数量最多的前cnt+1个集合合并,这样可以保证使用cnt条边后,合并完的集合度是比其他任何情况都要大。
(3)按照上述过程模拟,计算出前cnt+1个集合的总点数sum,则最大度为sum-1,输出答案即为所求。
2、时间复杂度
时间复杂度为O(n2logn)
3、代码详解
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int p[N],num[N],nums[N]; //p[]存储每个结点的祖宗结点,num[]存储集合大小,nums[]存储集合合并后每个合并后集合的点数
//并查集查找祖宗结点
int find(int x){if(p[x]!=x) p[x]=find(p[x]);return p[x];
}
//按降序排列cmp函数
bool cmp(int A,int B){return A>B;
}
int main(){int n,d;cin>>n>>d;//初始化并查集数组for(int i=1;i<=n;i++){p[i]=i;num[i]=1;}int cnt=0; //cnt记录满足前i个需求后还剩余多少条边while(d--){int x,y;cin>>x>>y;if(find(x)!=find(y)){ //如果x、y不在一个集合中,则合并num[find(y)]+=num[find(x)];p[find(x)]=find(y);}else cnt++; //如果x,y已经在一个集合中则无需操作,可以省下一条边可以使用int t=0;//将每个集合中点的数量记录在nums数组中for(int i=1;i<=n;i++){if(p[i]==i){nums[t++]=num[i];}}sort(nums,nums+t,cmp); //降序排列nums数组int sum=0; //取前cnt+1个点数最多的集合,将它们的点数记录在sum中for(int i=0;i<t&&i<cnt+1;i++){sum+=nums[i];}cout<<sum-1<<endl; //sum-1即为所求}return 0;
}
相关文章:

【蓝桥杯集训·周赛】AcWing 第92场周赛
文章目录第一题 AcWing 4864. 多边形一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4865. 有效类型一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4866. 最大数量一、题目1、原…...

编程参考 - GCC中的Basic ASM
asm关键字允许你在C代码中嵌入汇编程序指令。GCC提供两种形式的内联asm语句。一种是基本asm语句,是没有操作数的语句(见基本asm),而另一种扩展asm语句(见扩展asm)包括一个或多个操作数。在函数内部混合使用…...
软考中级-操作系统
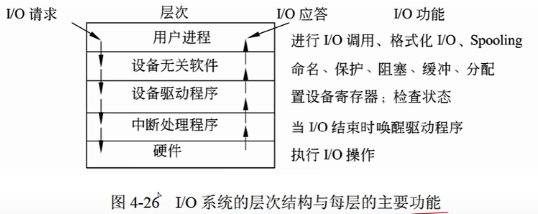
1 操作系统地位计算机系统由硬件和软件组成,未配置软件的称为裸机,但这会导致效率低下。操作系统是为弥补用户与硬件之间的鸿沟的一种系统软件,汇编、编译、解释、数据库管理系统等系统软件和其他应用软件都在此基础。2 进程管理又称处理机管…...

MYD-Y6ULL开发笔记
MYD-Y6ULL开发 文章目录MYD-Y6ULL开发一、系统移植1. 核板说明2. 文件系统操作二、应用开发1. 应用自启动2. 应用编译3.系统应用4.网络5.系统参数一、系统移植 1. 核板说明 型号 MYIR-Y6UL Y2 V2-256N 256D-50I烧了固件命令 uuu.exe myd-y6ulx-y2-256n256d-core-base.auto2. 文…...
三天吃透Java虚拟机面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

Spring Cloud Alibaba全家桶(二)——微服务组件Nacos注册中心
前言 本文为微服务组件Nacos注册中心相关知识,下边将对什么是 Nacos,Nacos注册中心(包括:注册中心演变及其设计思想、核心功能),Nacos Server部署(包括:单机模式、集群模式ÿ…...
命令执行漏洞 | iwebsec
文章目录1 靶场环境2 命令执行漏洞介绍3 靶场练习01-命令执行漏洞02-命令执行漏洞空格绕过03-命令执行漏洞关键命令绕过04-命令执行漏洞通配符绕过05-命令执行漏洞base64编码绕过4 命令执行漏洞危害01-读写系统文件02-执行系统命令03-种植恶意木马04-反弹shellpython反弹shellp…...

2023.02.26 学习周报
文章目录摘要文献阅读1.题目2.摘要3.介绍4.模型4.1 SESSION-PARALLEL MINI-BATCHES4.2 SAMPLING ON THE OUTPUT4.3 RANKING LOSS5.实验5.1 数据集5.2 验证方式5.3 baselines5.4 实验结果6.结论深度学习元胞自动机1.定义2.构成3.特性4.思想5.统计特征流形学习1.降维2.空间3.距离…...
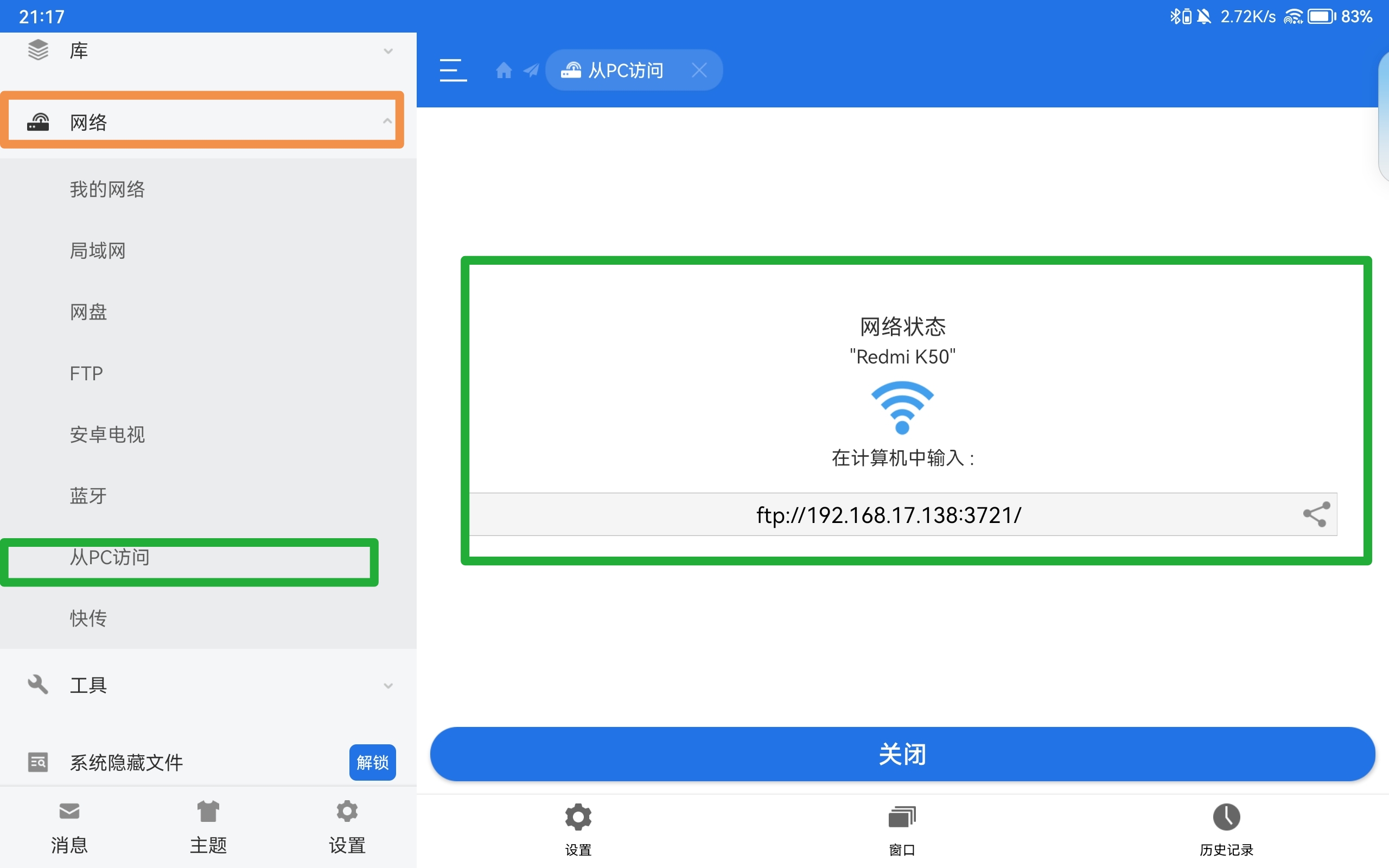
局域网实现PC、Pad、Android互联
文章目录局域网实现PC、Pad、Android互联一、网络邻居1、 Windows 配置1.1 开启共享功能1.2 设置用户1.3 共享文件夹2、 Pad 连接二、 FTP & HTTP1、 电脑配置1.1 HTTP 服务1.2 FTP 服务2、 连接3、 电脑连接 FTP三、 其他方式局域网实现PC、Pad、Android互联 在我们使用多…...
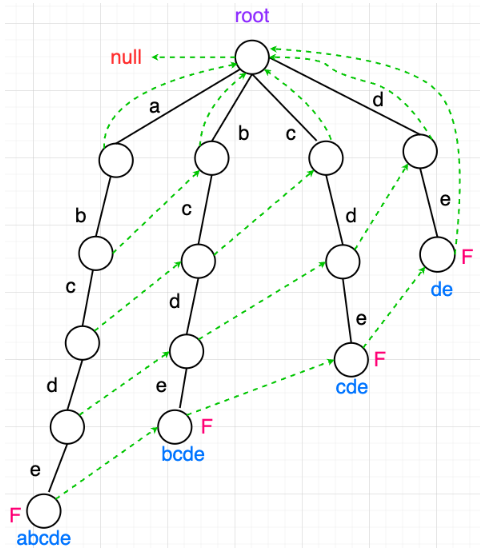
AC自动机
AC自动机 该模型应用场景是什么样的?假如有一篇很长的文章,然后有一个敏感词表单,请从这篇文章里找出包含了哪些敏感词。即便是用KMP进行快速匹配,那也只能每次遍历整篇文章才能找到一种敏感词,KMP只适用于单一子串匹配…...

git入门
目录 1. git简介 1.1 git是什么 1.2 git与svn的区别 2. github 2.1 创建仓库 2.2 删除仓库 2.3 新建文件及文件夹 3. git的基本操作 3.1 配置账户及邮箱 3.2 git文件状态与工作区域 3.3 常用命令 3.4 克隆(clone) 3.5 查看git仓库的状态 3.…...
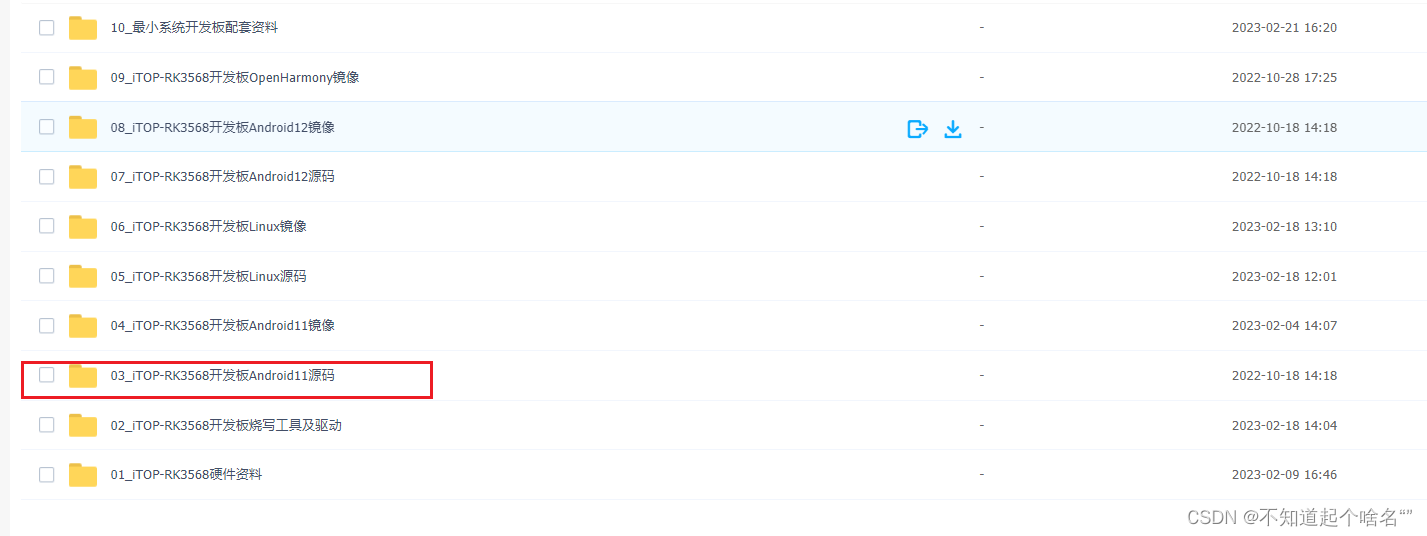
RK3568编译Android11和目录讲解
文章目录 前言一、下载android11源码二、环境搭建1.增加交换内存三、编译瑞芯微原厂源码四、目录讲解总结前言 本文记录在Ubuntu18.04中编译Android11,只有编译了源码,后面才能进行驱动的开发,有兴趣的小伙伴可以和我一起学习吧! 提示:以下是本篇文章正文内容,下面案例可…...
)
java泛型学习篇(二)
java泛型学习篇(二) 1 自定义泛型类 1.1 基本语法 Class 类型 <T,R,M...>{ //成员,其中...代表<>括号里面的参数可以有多个ja }1.2 注意点 1.2.1 属性和方法都是可以使用泛型的 T t;//属性使用泛型,合法public T getT() {return t;} //方法使用泛型,合法 publi…...

Java基础
Java基础Java基础一、课前问答二、概述三、Java的历史四、Java的特点五、计算机执行机制以及Java执行机制5.1 计算机的执行机制5.2 Java的执行机制六、常用DOS命令七、第一个Java程序八、包的使用九、编码规范十、注释Java基础 一、课前问答 1、什么是程序 2、什么是语言 3、什…...

骨骼控制(一)——动画动态节点(AnimDynamics)
文章目录一、引言二、骨骼控制三、UE蓝图中提供的骨骼控制节点——AnimDynamics动画蓝图节点1、什么是AnimDynamics动画蓝图节点①使用盒体计算惯性②使用约束来限制移动2、AnimDynamics节点的几种常用例子①单骨骼模拟②骨骼链模拟 <h2 id1>③群魔乱舞(这是错…...
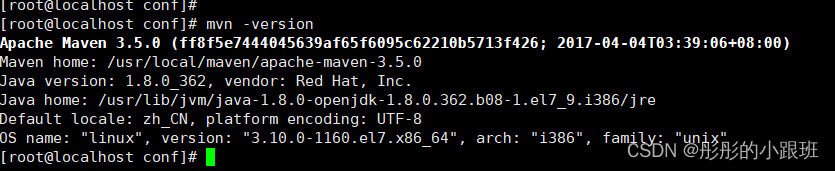
Linux系统下搭建maven环境
文章目录前述从官网下载安装包安装 maven修改maven配置修改环境变量测试前述 安装 maven 环境前,需要先安装 java 环境,如果没有安装 java 环境,可以参考:https://blog.csdn.net/weixin_45583303/article/details/118631855 从官…...

English Learning - L2 语音作业打卡 Day3 2023.2.23 周四
English Learning - L2 语音作业打卡 Day3 2023.2.23 周四💌 发音小贴士:💌 当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音[ ɔ: ]&…...

RK3568平台开发系列讲解(驱动基础篇)GIC v3中断控制器
🚀返回专栏总目录 文章目录 一、什么是GIC二、GIC v3中断类型三、GIC v3基本结构3.1、Distributor3.2、CPU interface简介3.3、Redistributor简介3.4、ITS(Interrupt translation service)4、中断状态和处理流程沉淀、分享、成长,让自己和他人都能有所收获!😄 📢ARM多核…...

决策树、随机森林、极端随机树(ERT)
声明:本文仅为个人学习记录所用,参考较多,如有侵权,联系删除 决策树 通俗来说,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话: 女儿&#x…...

软件测试之因果图法
因果图法 1. 概述 因果图法是一种**利用图解法分析输入条件、输出结果的各种组合情况,**从而设计测试用例的方法. 因果图法适用于有多个输入和多个输出,而且输入和输入之间有相互的组合关系,输入和输出之间有相互的制约和依赖关系. 使用场景和判定表…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
