AcWing 102. 最佳牛围栏(前缀和+二分+DP)
AcWing 102. 最佳牛围栏
1、问题
2、分析
(1)暴力做法
看到这道题以后,我们可以先想一个最暴力的做法,就是我们去枚举所有长度至少为 F F F的区间,然后求出这个区间的和,再求出这个区间的平均值。最后在这些平均值之间取一个最大值。
那么这个暴力做法的时间复杂度是多少呢?枚举所有符合长度要求的区间,该过程在最坏条件下的复杂度是 O ( n 2 ) O(n^2) O(n2),求出区间的和,复杂度是 O ( n ) O(n) O(n)。那么总的时间复杂度就是 O ( n 3 ) O(n^3) O(n3)。
很明显这个做法是超时的,那么对于这个暴力的做法,我们可以给出一个小小的优化,即我们通过前缀和算法将求区间的时间复杂度优化到 O ( 1 ) O(1) O(1),优化后,该做法的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。优化后依旧是超时的。
(2)二分答案+前缀和+DP
受朴素做法的启发,我们先求一下前缀和,将前缀和数组记作: s [ i ] s[i] s[i]。
这道题我们可以换个思路想,假设给你一个平均值 x x x。我们要做的是判断这个平均值是否能够达到。
换句话说,我们就是要判断是否存在一个区间,使得这个区间和的平均值达到了 x x x。
将其转化为数学表达式即:
是否存在一个区间 [ i , j ] [i,j] [i,j],其中 i − j + 1 > = F i-j+1>=F i−j+1>=F,满足:
s [ i ] − s [ j − 1 ] i − j + 1 ≥ x \frac{s[i] - s[j - 1]}{i-j+1} \geq x i−j+1s[i]−s[j−1]≥x
等价于
s [ i ] − s [ j − 1 ] ≥ x ∗ ( i − j + 1 ) s[i] - s[j - 1] \geq x * (i-j+1) s[i]−s[j−1]≥x∗(i−j+1)
等价于
a [ j ] + a [ j + 1 ] + . . . + a [ i ] ≥ x + x + . . . + x a[j]+a[j+1]+...+a[i]\geq x+x+...+x a[j]+a[j+1]+...+a[i]≥x+x+...+x
等价于
( a [ j ] − x ) + ( a [ j + 1 ] − x ) + . . . + ( a [ i ] − x ) ≥ 0 (a[j]-x)+(a[j+1]-x)+...+(a[i]-x)\geq 0 (a[j]−x)+(a[j+1]−x)+...+(a[i]−x)≥0
如果我们设 b [ i ] = a [ i ] − x b[i]=a[i]-x b[i]=a[i]−x, b [ i ] b[i] b[i]的前缀和数组为 T [ i ] T[i] T[i]的话,
上述式子即可转化为:
T [ i ] − T [ j − 1 ] ≥ 0 T[i]-T[j-1]\geq0 T[i]−T[j−1]≥0
如果想要找到这样一个合法区间,我们只需要找到一个平均值最大的区间,看看它是否到达 x x x即可。
因此,我们可以枚举区间右端点 i i i,即固定 T [ i ] T[i] T[i],要想让 T [ i ] − T [ j − 1 ] T[i]-T[j-1] T[i]−T[j−1]最大,只要找到最小的 T [ j − 1 ] T[j-1] T[j−1]即可。该过程可以用 D P DP DP来做。
这个 D P DP DP比较简单,定义 d p [ i ] dp[i] dp[i]为前 i i i个 T [ i ] T[i] T[i]中最小的一个。
转移方程为: d p [ i ] = m i n ( d p [ i − 1 ] , T [ i ] ) dp[i] = min(dp[i-1],T[i]) dp[i]=min(dp[i−1],T[i])
那么我们的 T [ i ] − T [ j − 1 ] T[i]-T[j-1] T[i]−T[j−1]的最大值即: T [ i ] − d p [ i − F ] T[i]-dp[i-F] T[i]−dp[i−F]
因为我们是枚举的 i i i,所以这个过程是 O ( n ) O(n) O(n)的。
也就是说我们只需要通过 O ( n ) O(n) O(n)的时间复杂度,就能够判断一个平均值 x x x是否能够达到。
因此,我们只需要去二分这个 x x x即可,即二分答案。
而通过题目,我们发现, x x x的最大值就是2000。
因此,总的时间复杂度就是: O ( n l o g ( 2000 ) ) O(nlog(2000)) O(nlog(2000))
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
using namespace std;
const int N = 1e5 + 10;
const double eps = 1e-5;
int n, f;
double a[N], T[N], dp[N];bool check(double mid)
{for(int i = 1; i <= n; i ++)T[i] = T[i - 1] + a[i] - mid;for(int i = 1; i <= n; i ++){dp[i] = min(dp[i - 1], T[i]);}for(int i = f; i <= n; i ++){if(T[i] - dp[i-f] >= 0)return true;}return false;
}void solve()
{cin >> n >> f;for(int i = 1; i <= n; i ++)cin >> a[i];double l = 0, r = 2000.0;while(r - l > eps){double mid = (l + r) / 2.0;if(check(mid))l = mid;elser = mid;} cout << (int)(r * 1000) << endl;
}signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;//cin >> t;while(t--)solve();
}
相关文章:
)
AcWing 102. 最佳牛围栏(前缀和+二分+DP)
AcWing 102. 最佳牛围栏 1、问题 2、分析 (1)暴力做法 看到这道题以后,我们可以先想一个最暴力的做法,就是我们去枚举所有长度至少为 F F F的区间,然后求出这个区间的和,再求出这个区间的平均值。最后在…...
React-表单受控绑定和获取Dom元素
一、表单受控组件 1.声明一个react状态 说明:useState const [value,setValue]useState("") 2.核心绑定流程 2.1绑定react状态 <div><input value{value}type"text"></input> 2.2绑定onChange事件 说明:e.…...
python hashlib模块及实例
hashlib 模块密码加密密码撞库密码加盐 一,hashlib模块 hashlib模块是用来为字符串进行加密的模块,通过该作用就可以为用户的密码进行加密。 通过模块中的hash算法可以为任意长度的字符串加密成长度相同的一串hash值。该hash算法得到的hash值有一下几个…...
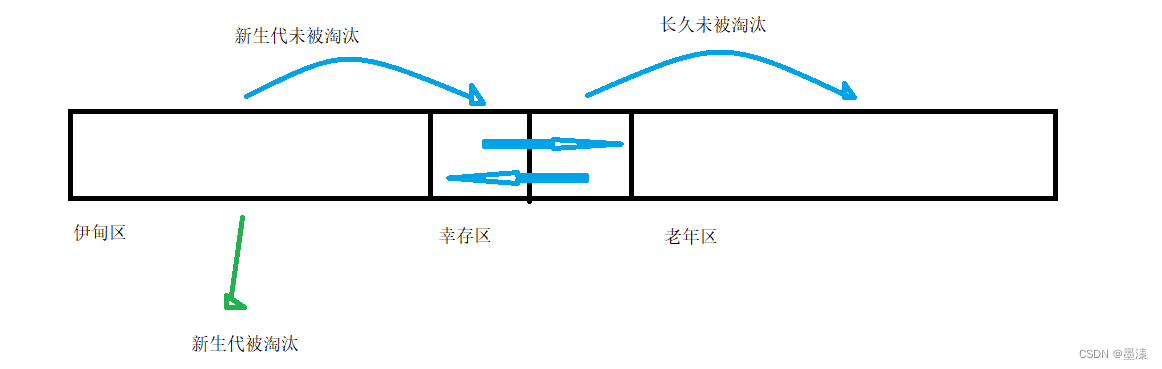
垃圾回收GC
为什么要有垃圾回收? JVM之所以要有垃圾回收,是因为它能够自动管理内存,避免内存泄漏和内存溢出的问题,垃圾回收机制会自动检测和清理不再使用的对象,释放内存空间,使得开发者不需要手动管理内存,降低了开发难度和错误风险,同时,垃圾回收还可以优化内存分配,提高程序性能和响…...
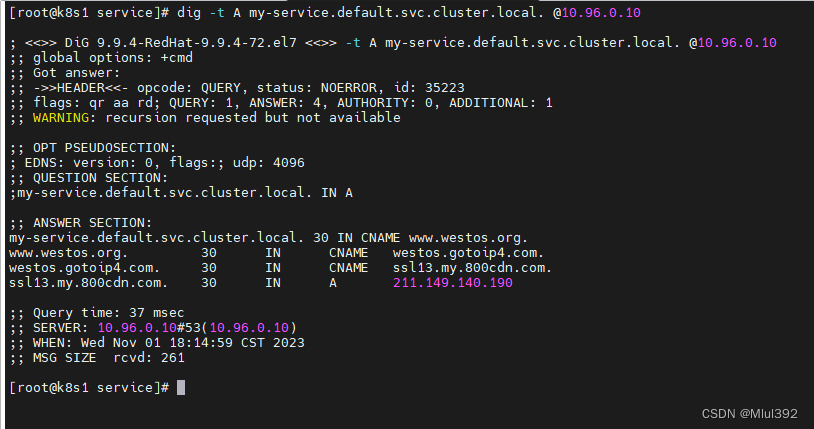
kubernetes-service微服务
目录 一、service微服务 二、Ipvs模式 三、ClusterIP 1.ClusterIP 2.headless 四、NodePort 1.NodePort 2.默认端口 五、LoadBalancer 1.LoadBalancer 2.metallb 六、ExternalName 一、service微服务 Kubernetes Service微服务是一种基于Kubernetes的微服务架构&…...

让你笑到不行的笑话短视频接口,快来试试!
11在当今这个快节奏的社会中,笑话成为了许多人调节情绪的有效方法。如今,短视频平台已经成为了最受欢迎的娱乐方式之一,因此,将笑话和短视频结合起来,成为了一种很有趣的方式来带给我们欢乐。今天我们要介绍的是挖数据…...
#MANDATORY)
系列四十五、Spring的事务传播行为案例演示(五)#MANDATORY
一、演示Spring的传播行为(MANDATORY) 1.1、StockServiceImplMANDATORY /*** Author : 一叶浮萍归大海* Date: 2023/10/30 15:43* Description: 演示MANDAORY的传播行为* 外部不存在事务:抛出异常 No existing transaction found for…...
-- String Manipulation(字符串处理工具))
idea插件(二)-- String Manipulation(字符串处理工具)
目录 1. 安装 String Manipulation 2. 默认快捷键 3. 操作说明 3.1 变量名的形式处理 3.2 文本形式的转化...

HQChart实战教程67-worker批量计算股票指标
HQChart实战教程67-worker批量计算股票指标 什么是Worker批量指标计算示例地址步骤1. 创建一个后台工作线程类2. 发送指标计算任务3. 接收计算结果数据对接 完整源码demo_workerthread_sina.htmlhqchart_worker_sina.js HQChart插件源码地址 什么是Worker Worker 接口是 Web W…...

博客系统自动化测试项目实践
文章目录 一.测试需求分析1.功能分析2.非功能分析 二.制定测试方案(计划 策略)三.编写测试用例四.执行自动化测试用例五.编写测试报告六.项目总结 一.测试需求分析 1.功能分析 通过功能测试需求分析 2.非功能分析 非功能分析主要从:界面,性能,安全性,…...
软考高级之系统架构师系列之操作系统基础
概念 接口 操作系统为用户提供两类接口:操作一级的接口和程序控制一级的接口。操作一级的接口包括操作控制命令、菜单命令等;程序控制一级的接口包括系统调用。 UMA和NUMA UMA,统一内存访问,Uniform Memory Access,…...

制作一个可以arm架构下运行的docker镜像(for Python)
看完本篇文章,你将得到一个可以arm架构下运行的python 基础镜像。 题外话 这里直接说docker镜像有点儿草率,因为目前很多容器都是Podman了。 podman的介绍 arm和aarch傻傻分不清楚 现在这两个是一样的意思了。 arm64和aarch64之间的区别 开始制作镜…...
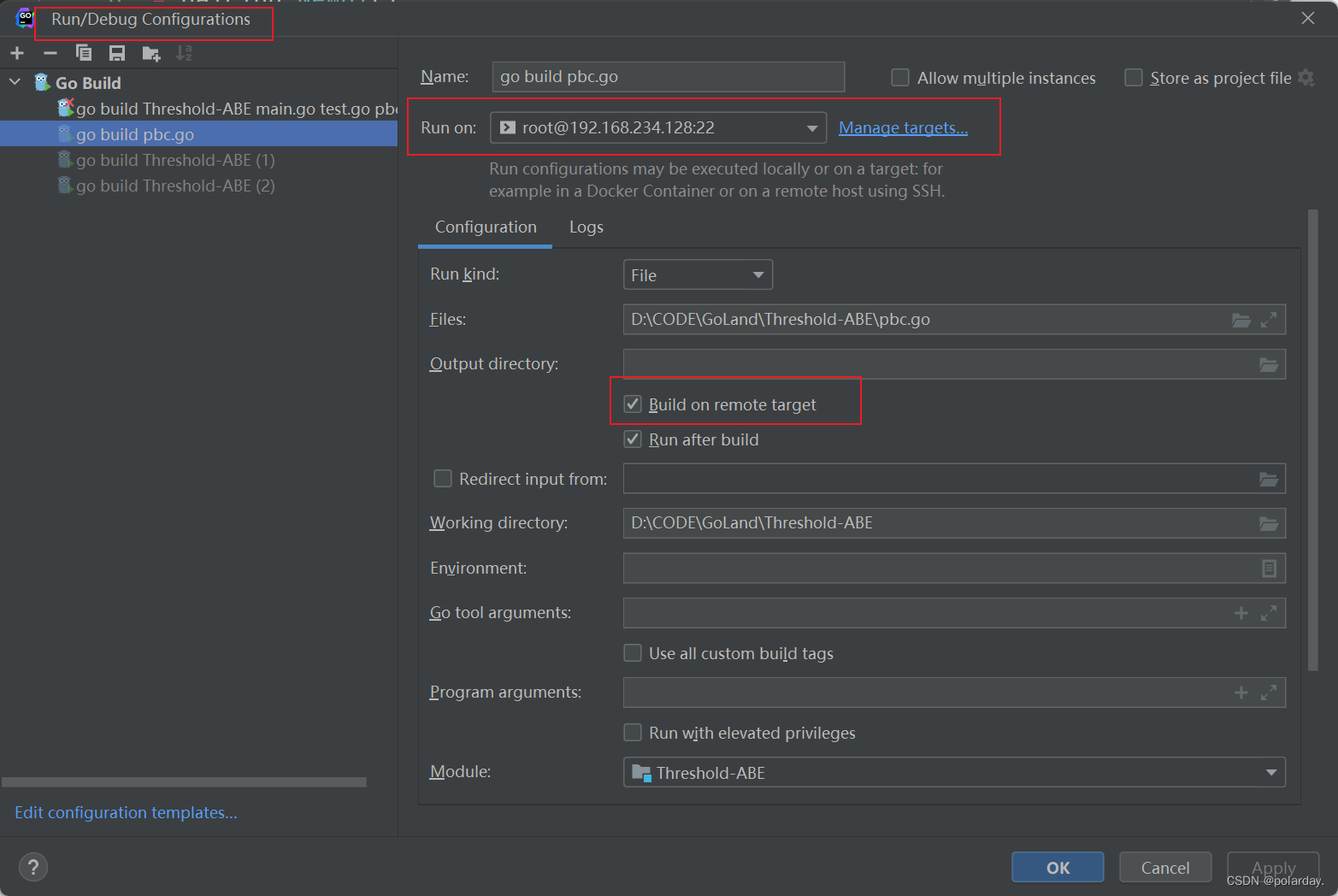
Goland连接服务器/虚拟机远程编译开发
创建SSH连接 SSH用于与远程服务器建立连接 Settings -> Tools -> SSH Configurations 添加新的ssh连接,Host为ip地址,Username为用户名,认证方式这里选择密码验证 全部填完后可以点击Test Connection测试连接是否成功 创建Deployment…...

大数据Doris(十四):Doris表中的数据基本概念
文章目录 Doris表中的数据基本概念 一、Row & Column...
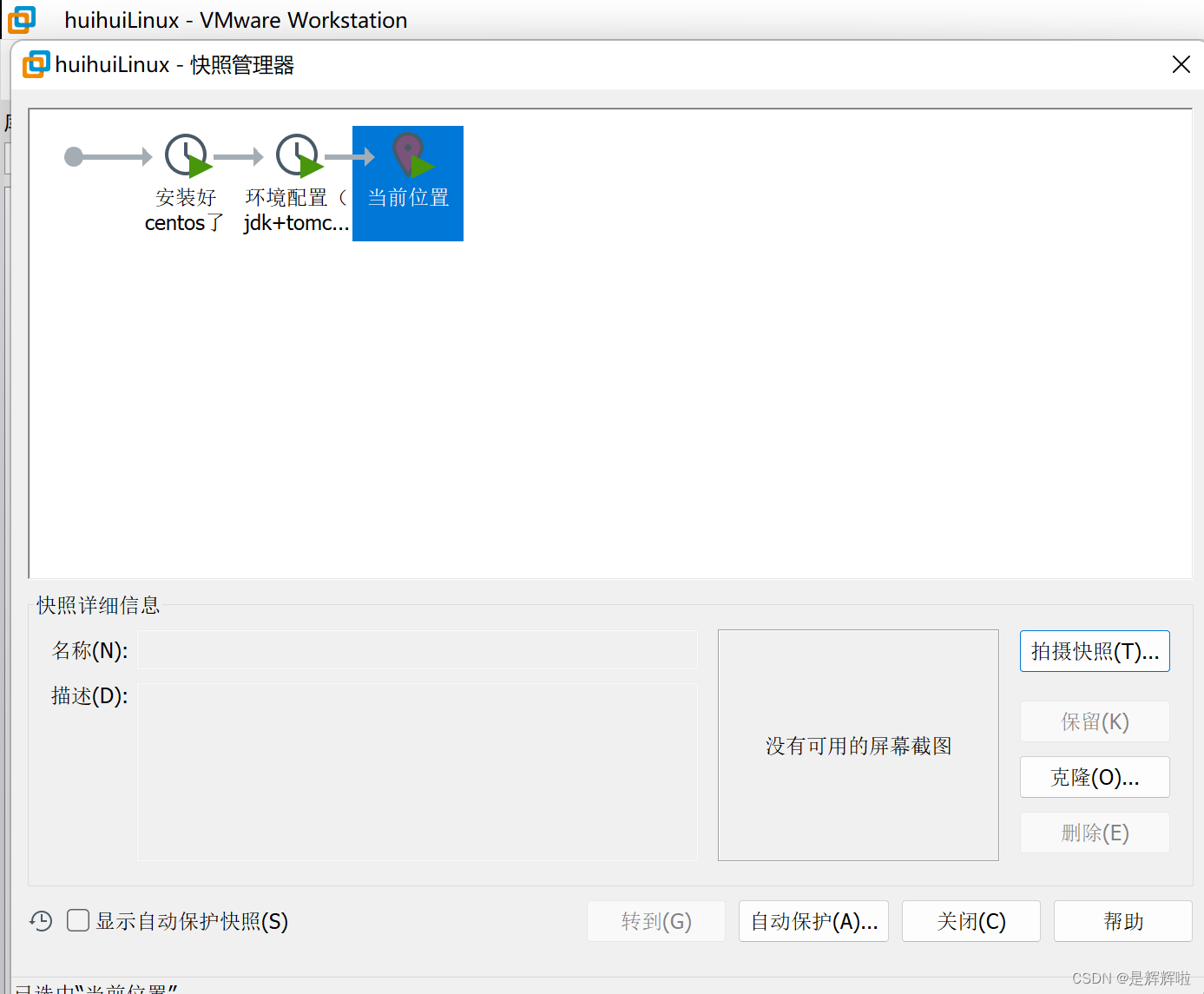
【Linux】Linux环境配置以及部署项目后端
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于Linux的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.Linux环境配置 1.JDK ①上传安装包到…...
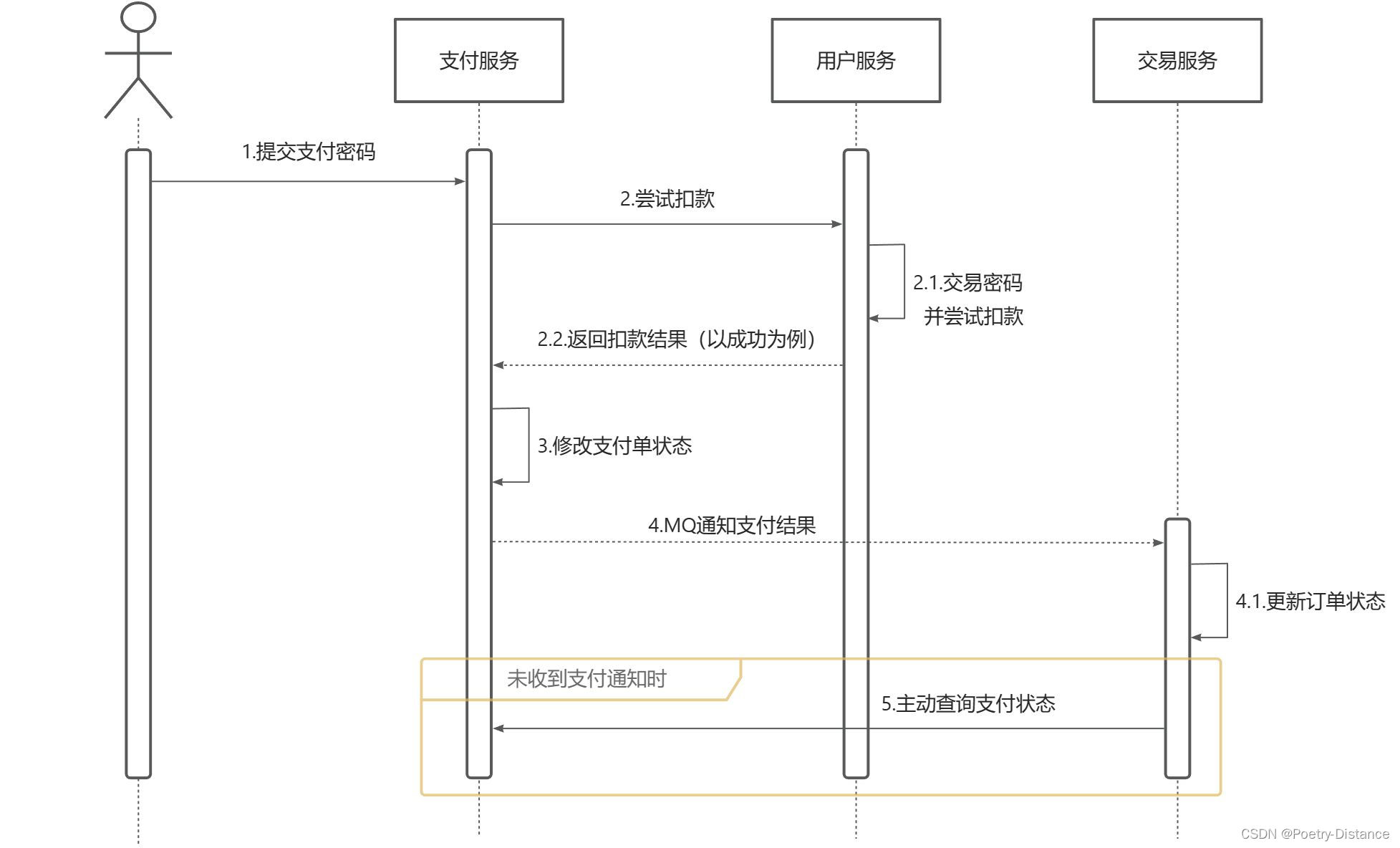
RabbitMQ消费者的可靠性
目录 一、消费者确认 二、失败重试机制 2.1、失败处理策略 三、业务幂等性 3.1、唯一消息ID 3.2、业务判断 3.3、兜底方案 一、消费者确认 RabbitMQ提供了消费者确认机制(Consumer Acknowledgement)。即:当消费者处理消息结束后&#x…...
云计算助力史上首届“云上亚运”圆满成功!
201金,魔幻的BGM,以及崛起的中国科技,让杭州亚运会成功出圈。 很多网友表示太震撼了!开幕式很漂亮,杭州为了奥运造新城真豪横,看完一整个文化自信住! 赛场内外除了无数个令人感动的瞬间&#…...

博彦科技:以金融为起点,凭借创新技术平台真打实干
【科技明说 | 重磅专题】 成立于1995年的博彦科技,已有28年左右的发展历程。 我没有想到,博彦科技也对AIGC领域情有独钟。博彦科技自研的数字人产品SaaS平台,可以接入包括百度文心一言、阿里通义千问等AI大模型产品。可见&#…...

NLP实践——中文指代消解方案
NLP实践——中文指代消解方案 1. 参考项目2. 数据2.1 生成conll格式2.2 生成jsonline格式 3. 训练3.1 实例化模型3.2 读取数据3.3 评估方法3.4 训练方法 4. 推理5. 总结 1. 参考项目 关于指代消解任务,有很多开源的项目和工具可以借鉴,比如spacy的基础模…...
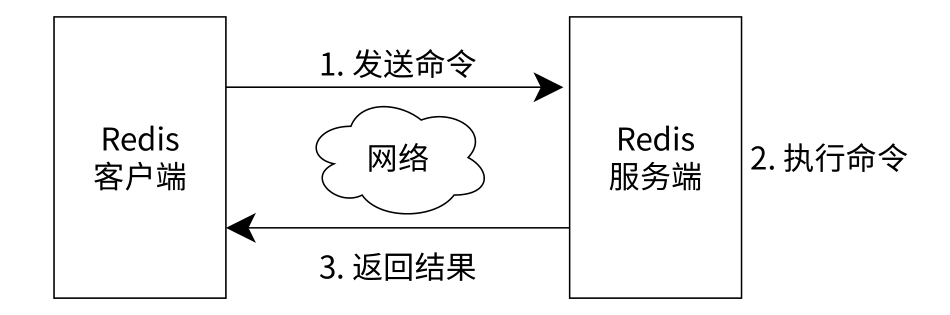
【Redis】认识Redis-特点特性应用场景对比MySQL重要文件及作用
文章目录 认识redisredis的主要特点redis的特性(优点)redis是单线程模型,为什么效率这么高,访问速度这么快redis应用场景redis不可以做什么MySQL和Redis对比启动RedisRedis客户端Redis重要文件及作用 认识redis redis里面相关的小…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

RFID推动新能源汽车零部件生产系统管理应用案例
RFID推动新能源汽车零部件生产系统管理应用案例 一、项目背景 新能源汽车零部件场景 在新能源汽车零部件生产领域,电子冷却水泵等关键部件的装配溯源需求日益增长。传统 RFID 溯源方案采用 “网关 RFID 读写头” 模式,存在单点位单独头溯源、网关布线…...

Python打卡训练营学习记录Day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
