论文-分布式-共识,事务以及两阶段提交的历史描述
- 这是一段关于一致性,事务以及两阶段提交的历史的描述
- 阅读关于一致性的文献可能会有些困难,因为:
- 各种用语在不断的演化着(比如一致性<consensus>最初叫做协商<agreement>);
- 各种研究成果并不是以一种逻辑性的顺序产生出来;
- 同时描述整个分布式算法的框架与这些研究工作又是平行地演化着;
- 此外除了Lynch的《分布式算法》外,很少有书籍涉及到这个主题
- 下面涉及的这些论文不是按照它们的发表顺序来进行介绍,而是尽量以最容易理解的方式来组织
- 所知道的第一个一致性问题实例应该是Lamport的“Time, Clocks and the Ordering of Events in a Distributed System” (1978),尽管它并没有明确的提出一致性(consensus)或者协商(agreement)的概念
- 在这篇论文里,Lamport讨论了消息如何在有限的时间内在不同处理器之间传输,同时还利用爱因斯坦的狭义相对论进行了有趣的比喻
- 早在1978年,Lamport就采用时空图给出了一个完整的全方位的分析
- 关键问题在于,在一个分布式系统中,你无法判断事件A是否发生在事件B之前,除非A和B存在某种依赖关系
- 每个观察者都可能看到不同的事件发生序列,除非这些事件相互之间存在依赖关系,即分布式系统中的事件仅仅是部分有序的
- Lamport定义了一个称为”发生在前”的关系和操作符,然后又给出了一个算法,用来确定分布式系统中的事件的全序关系,这样所有的进程就可以看到与其他进程一样的事件排序
- 同时,Lamport还提出了分布式状态机的概念:
- 让一组确定性状态机从相同的初始状态开始,之后保证它们以相同的顺序处理相同的消息
- 这样就可以保证每个状态机都是其他状态机的一个副本
- 关键的问题就是让每个状态机在“哪个消息是下一个需要处理的消息”这个问题上达成一致,这就是一个一致性问题
- 这就是一个创建事件排列的算法所需要做的,提供一个关于消息传输顺序的统一约定
- 然而,这个系统并不是容错的,如果一个进程出错,其他进程将无限等待下去直到它恢复
- 大概在这篇论文发表的同一时间,JimGray在“Notes on Database Operating Systems” (1979)中描述了两阶段提交(2PC)
- 不幸的是,如果事务管理器在某个错误的时间点失败的话,2PC就会被阻塞
- Dale Skeen在“NonBlocking Commit Protocols” (1981)中指出,对于一个分布式系统,需要3阶段的提交算法来避免2PC中的阻塞问题
- 问题关键在于找到一个好的3PC算法,这已花费了将近25年
- Fischer, Lynch 和 Paterson在“Impossibility of distributed consensus with one faulty process” (1985)中指出对于一个异步系统来说即使只有一个进程出错,分布式一致性也是不可能达到的,这就是著名的FLP结论
- 直到此时,consensus才成为“让一系列处理器在一个value上达成共识的”这一问题的叫法
- 在一个具有完美网络(所有的消息都会被传输,按序到达,不会重复)的异步系统(处理器以任意的速率运行,处理器间的消息传输可能花费任意时长)中,只要有一个出错进程(即使只有一次故障)分布式一致性就是不可能的
- 问题的核心在于,你无法区分一个进程到底是终止了还是正在以极低的速度执行,这使得在异步系统中的错误处理几乎是不可能的
- 此外这篇论文的重要性还在于它展示了如何证明某些事情是不可能的:首先证明解决该问题的算法都必须满足一些属性,然后证明满足这些属性是不可能的,比如通过反证法证明(这种方法曾经被图灵用于停机问题的证明中)
- 此时,人们意识到一个分布式算法具有两个属性:安全性(safety)和活性(liveness)
- 安全性意味着坏的事情不会发生,而活性意味着某些好的事情最终一定会发生
- 2PC作为一个一致性算法,用来保证所有的进程在“事务要么提交要么失败退出”上达成一致
- 2PC是安全的,不会有坏的数据被写入到数据库,但是它的活性并不好:如果事务管理器在一个错误的点上失败,那么系统会阻塞
- 也是在此时,人们意识到可以将一个分布式系统分为同步的(进程以已知的速率运行,消息会在限制的时间内传输)和异步的(进程以未知的任意的速率运行,消息的传输时间没有上界)
- 异步与同步相比,是一种更通用的情况
- 一个适用于异步系统的算法,也能被用于同步系统,但是反过来并不成立
- 你可以将同步系统看做是异步系统的一个特殊情况,只是消息传输时间恰好有个上界
- 在FLP之前,还有这样一篇论文“The Byzantine Generals Problem” (1982)
- 在这种形式的一致性问题中,进程还可能会说谎,而且它们还会尽力地去欺骗其他进程
- 这个问题看起来比FLP更难,但是对于同步的情况它确实存在一个解(尽管当这篇论文发表的时候,同步和异步系统的区分还没有明确提出)
- 但是这个解代价很高,需要大量多轮的消息传递
- 这个问题最初来源于航天工业:如果飞机上的传感器给出错误的信息会怎么样呢?(很明显,这个系统被认为是同步的)
- 在1986年,分布式系统领域关注一致性和事务的人们聚在了一起
- 在那个时候,最好的一致性算法就是Byzantine Generals,但是这个算法代价太高而无法用于事务处理
- 关于这场会议JimGray写了一篇文章“A Comparison of the Byzantine Agreement Problem and the Transaction Commit Problem.” (1987),这篇论文的导引里有如下的语句:
- “在这次会议之前,人们普遍认为分布式系统中的事务提交问题是拜占庭将军问题的一个退化版本;或许这次会议的最大意义在于指出二者很少有共同点”
- 最终,分布式事务被认为是一个新的一致性问题,称为uniform consensus (参见“Uniform consensus is harder than consensus” (2000))
- 在uniform consensus中,所有的进程都必须在一个value上达成一致,即使是那些出错的进程
- 一个事务当且仅当所有的RM都准备好提交时才会被提交
- 而大多数的一致性问题只关注那些没有出错的进程可以达到一致
- 因此,uniform consensus比普通的一致性问题要难
- 最终Lamport在“The Part-Time Parliament” (submitted in 1990, published 1998)中提出了Paxos一致性算法,不幸的是采用希腊民主议会的那个比喻很明显失败了,因为人们觉得这篇论文太难理解了
- 所以这篇论文就被不幸的忽略了,直到Butler Lampson在“How to Build a Highly Availability System using Consensus” (1996)中重新提到这个算法
- 这篇论文对如何构建容错系统和Paxos进行了很好的介绍
- 后来Lamport又发表了“Paxos Made Simple (2001)
- Paxos的核心是:给定固定数目的进程,任何一个多数者集合与其他的多数者集合必然至少存在一个公共元素
- 比如给定三个元素A,B和C
- 那么可能的多数者集合是AB, AC, 或者 BC
- 当一个决定由其中一个多数者集合比如AB通过时,那么在以后的任何时刻其他的多数者集合中至少有一个元素能够记住之前的多数者集合做出的决定
- 比如对于多数者集合AB,那么A,B会记住决定,对于AC,A会记得,对于BC,B还记得
- Paxos可以容忍消息的丢失,延迟,重传和乱序
- 只要存在一个leader可以跟进程中的一个多数者集合会话两次,就能达到一致性
- 任何进程,包括leader在内,都可以失败或重启,实际上所有的进程可以在同一时间失败掉,而算法仍然是安全的
- 同一时间,可能有不止一个leader
- Paxos是一个异步算法,没有显式的超时设置
- 然而只有当系统表现出同步的方式时,它才能达到一致性
- 比如消息要在一定的时间内传输
- 根据FLP结论,存在一种病态的情况,Paxos在这种情况下无法达到一致性,但是在实际中避免出现这种情况相对容易些
- 将一个系统简单的划分为同步异步有些宽泛
- Dwork, Lynch 和 Stockmeyer在“Consensus in the presence of partial synchrony” (1988)中定义了部分同步系统
- 存在两种类型的部分同步系统:其中一种情况是进程以给定边界内的速率运行,消息传输时间是有界的,但是边界的实际取值事先无法得知;
- 另一种情况是处理速度的边界以及消息传输上界事先已知,但是只在未来的某个未知时间才开始成立
- 对于现实世界来说,部分同步模型是一个比同步异步模型更好的模型
- 大部分时间网络行为都是以一种可预测的方式发生,但是可能突然会变得很疯狂
- 在“Consensus on Transaction Commit” (2005)中,Lamport和Jim Gray将Paxos应用在分布式事务提交问题中
- 他们使用Paxos来对2PC中的事务管理器进行高效的备份
- 对于事务中涉及的每个RM使用一个Paxos的实例来决定该RM(resource manager,实际上就是该事务涉及的进程)是否提交该事务
- 在这里面,为每个RM使用一个Paxos实例看起来很昂贵,但是实际证明情况并不是这样
- 对于没有错误发生的情况下,Paxos提交可以通过两个阶段完成,与2PC相比尽管有更多的消息需要传输但具有相同的消息延迟
- 只有当错误发生时,才需要第3个阶段
- 给定2n+1个事务管理器,当错误副本数小于等于n时,Paxos提交都可以完成
- Paxos提交并没有使用Paxos算法来直接解决事务提交问题,它并不是用来解决uniform consensus,而是用来让系统容错
- 有一种观点认为分布式事务不应该被使用,因为2PC是阻塞失效的
- Paxos提交就是用来解决阻塞的问题
- 有一些关于CAP(Consistency(一致性), Availability(可用性) 和 Partition tolerance(分区容错性))猜想的讨论
- 这个猜想指出,在分布式系统中,无法同时满足上述三个属性(即在分布式系统的设计中,无法同时满足对数据的实时一致性要求、完全无故障的可用性以及分区容错性)
- 我们可以将Consistency等同于consensus(共识)来检验下CAP
- 根据FLP结论,在一个异步系统中,当出现一个出错进程时,无法达到consensus
- 所以对于一个异步系统来说,我们无法同时得到Consistency和Availability(在网络分区(网络故障)的情况下,系统需要在可用性和一致性之间作出选择,即是选择保持可用性而降低一致性,还是放弃一些可用性以维持一致性)
- 假设现在有一个包含三个节点A,B和C的Paxos系统
- 如果有2个节点在工作,我们就能达到一致性,即我们可以得到consistency 和 availability
- 现在如果C被分割,而且有查询请求,它就会因无法与其他节点通信而无法响应{!这样就不具有可用性了}
- 它无法判断到底是自己被分割了,还是其他两个节点down掉了,又或者是网速很慢
- 其他两个节点可以正常进行,因为它们相互可以通信并形成一个多数者集合
- 所以对于CAP猜想,Paxos无法处理网络分割,因为C无法对查询做出响应
- 然而在工程上,我们可以绕过这个问题
- 假设我们处在一个数据中心内部,可以使用两套独立网络(Paxos并不介意出现重复消息)
- 如果我们是在因特网上,我们可以让客户端查询所有的节点A,B,C
- 如果C被分割了,它可以查询A或者B,除非它跟C一样被分割了
- 对于一个同步网络,如果C被分割了,如果它在一定的时间内收不到消息就可以知道自己被分割了,因此能够向客户端声明自己down掉了
相关文章:

论文-分布式-共识,事务以及两阶段提交的历史描述
这是一段关于一致性,事务以及两阶段提交的历史的描述阅读关于一致性的文献可能会有些困难,因为: 各种用语在不断的演化着(比如一致性<consensus>最初叫做协商<agreement>); 各种研究成果并不是以一种逻辑性的顺序产生…...
)
[100天算法】-二叉树剪枝(day 48)
题目描述 给定二叉树根结点 root ,此外树的每个结点的值要么是 0,要么是 1。返回移除了所有不包含 1 的子树的原二叉树。( 节点 X 的子树为 X 本身,以及所有 X 的后代。)示例1: 输入: [1,null,0,0,1] 输出: [1,null,0,null,1]示例2: 输入: […...
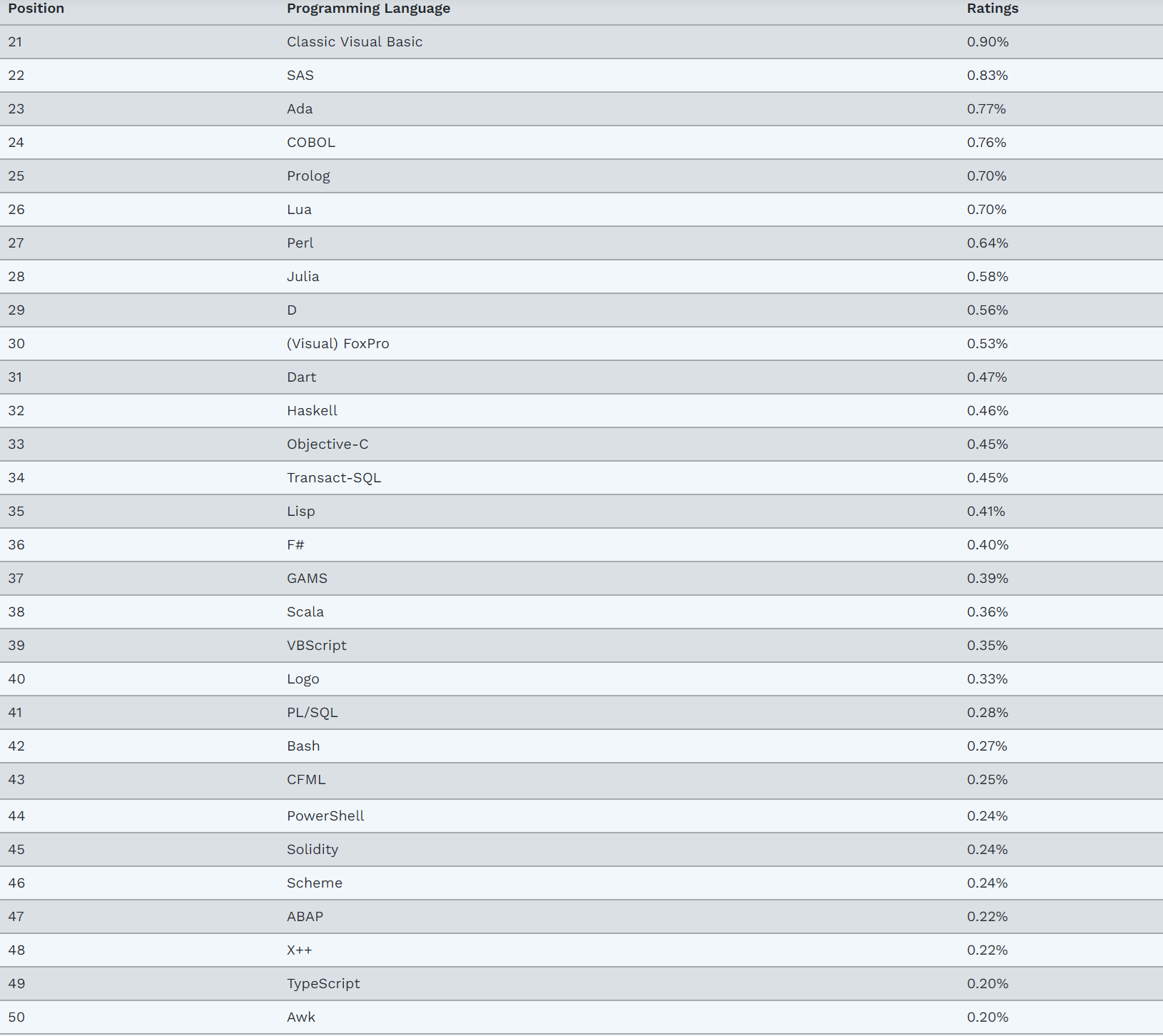
常用编程语言排行与应用场景汇总(2023.10)
文章目录 编程语言排行一、Python二、C三、C四、Java五、C#六、JavaScript七、VB(Visual Basic)八、PHP九、SQL十、ASM(Assembly Language)十一、Go十二、Scratch十三、Delphi/Object Pascal十四、MATLAB十五、Swift十六、Fortran…...
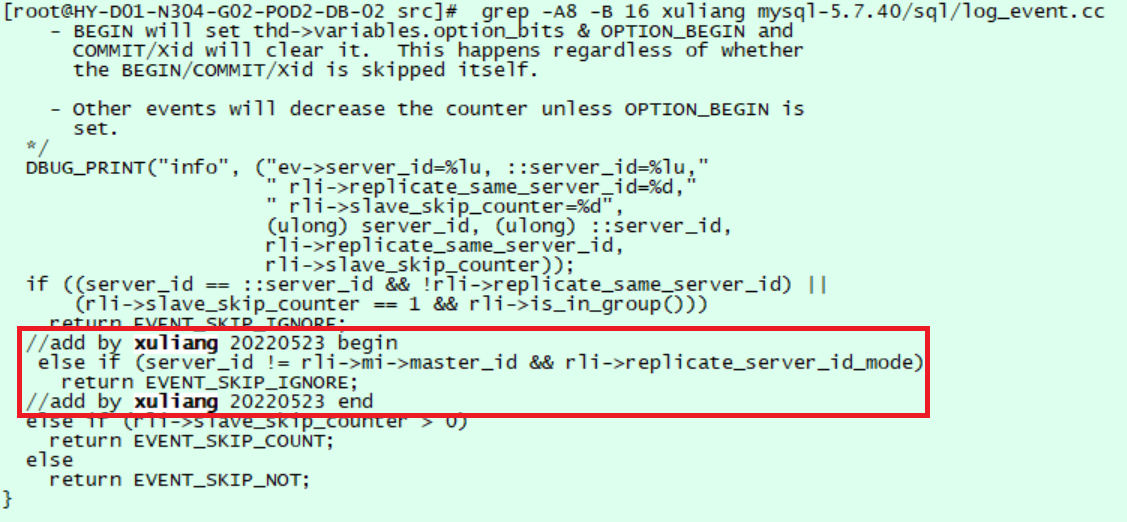
基于 MySQL 多通道主主复制的机房容灾方案
文章中介绍了多种 MySQL 高可用技术,并介绍了根据自身需求选择多通道主主复制技术的过程和注意事项。 作者:徐良,现任中国移动智慧家庭运营中心数据库高级经理,多年数据库运维优化经验,历任华为、一线互联网公司高级 D…...
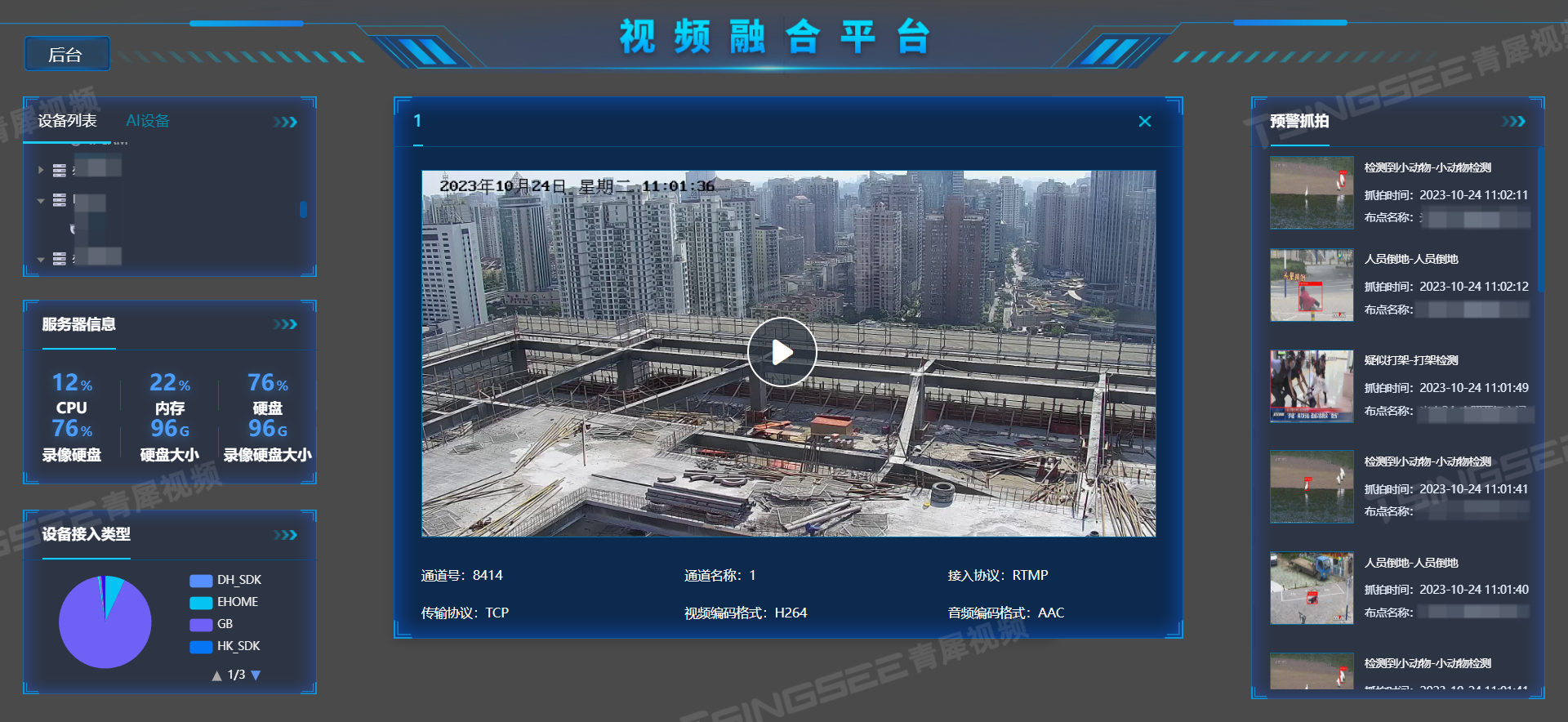
视频汇聚平台EasyCVR分发的流如何进行token鉴权?具体步骤是什么?
视频监控EasyCVR平台能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,TSINGSEE青犀视频安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多路视频流,也能支持视…...
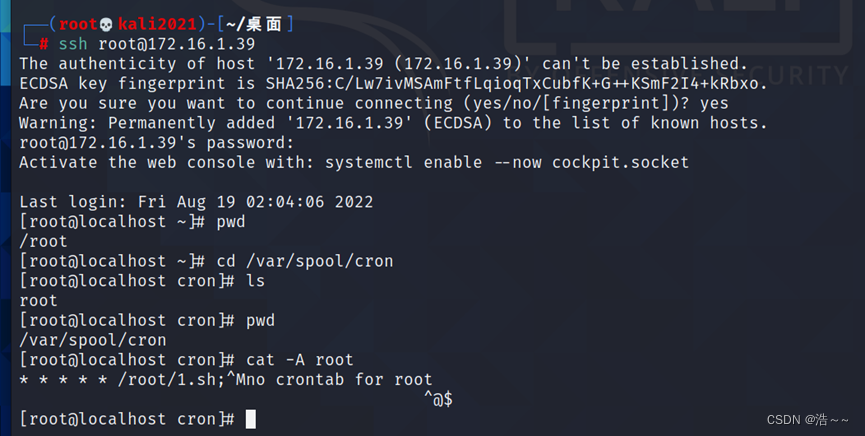
B-5:网络安全事件响应
B-5:网络安全事件响应 任务环境说明: 服务器场景:Server2216(开放链接) 用户名:root密码:123456 1.黑客通过网络攻入本地服务器,通过特殊手段在系统中建立了多个异常进程,找出启动异常进程的脚本,并将其绝对路径作为Flag值提交; 通过nmap扫描我们发现开启了22端口,…...

第17期 | GPTSecurity周报
GPTSecurity是一个涵盖了前沿学术研究和实践经验分享的社区,集成了生成预训练 Transformer(GPT)、人工智能生成内容(AIGC)以及大型语言模型(LLM)等安全领域应用的知识。在这里,您可以…...

透视俄乌网络战之五:俄乌网络战的总结
透视俄乌网络战之一:数据擦除软件 透视俄乌网络战之二:Conti勒索软件集团(上) 透视俄乌网络战之三:Conti勒索软件集团(下) 透视俄乌网络战之四:西方科技巨头的力量 俄乌网络战总结 1…...
深度学习之基于Pytorch卷积神经网络的图像分类系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介二、功能三、图像分类系统四. 总结 一项目简介 基于PyTorch卷积神经网络的图像分类系统是一种应用深度学习技术来实现图像分类任务的系统。本摘要将对该系统…...

外观专利怎么申请?申请外观专利需要的资料有哪些?
专利分为发明专利、实用新型专利和外观设计专利三类。 我国专利法规定,发明专利的保护期限最长,为自申请日起20年。同时,由于需要进行实质审查,发明专利的审查周期也相对较长,往往需要2年甚至更长时间才能获得授权。 随…...

【Amazon】跨AWS账号资源授权存取访问
文章目录 一、实验框架图二、实验过程说明三、实验演示过程1、在A账号中创建S3存储桶2、在A账号创建S3存储桶访问策略3、在A账号创建信任开发账号的角色4、在B账号为用户添加内联策略5、在B账号中切换角色,以访问A账号中的S3资源 四、实验总结 一、实验框架图 本次…...

探索C++中的不变之美:const与构造函数的深度剖析
W...Y的主页😊 代码仓库分享💕 🍔前言: 关于C的博客中,我们已经了解了六个默认函数中的四个,分别是构造函数、析构函数、拷贝构造函数以及函数的重载。但是这些函数都是有返回值与参数的。提到参数与返回…...

DDoS类型攻击对企业造成的危害
超级科技实验室的一项研究发现,每十家企业中,有四家(39%)企业没有做好准备应对DDoS攻击,保护自身安全。且不了解应对这类攻击最有效的保护手段是什么。 由于缺乏相关安全知识和保护,使得企业面临巨大的风险。 当黑客发动DDoS攻击…...

深入理解JVM虚拟机第十五篇:虚拟机栈常见异常以及如何设置虚拟机栈的大小
大神链接:作者有幸结识技术大神孙哥为好友,获益匪浅。现在把孙哥视频分享给大家。 孙哥链接:孙哥个人主页 作者简介:一个颜值99分,只比孙哥差一点的程序员 本专栏简介:话不多说,让我们一起干翻JavaScript 本文章简介:话不多说,让我们讲清楚JavaScript里边的Math 文章目…...

Rocketmq5延时消息最大时间
背景 Rocketmq5中支持延时消息的时间,通过Message.setDelayTimeSec可以设置延时消息的精确时间。 问题 当设置时间超过3天时出现异常 org.apache.rocketmq.client.exception.MQBrokerException: CODE: 13 DESC: timer message illegal, the delay time should no…...

uniapp @click点击事件在新版chrome浏览器点击没反应
问题描述 做项目时,有一个弹出选择的组件,怎么点都不出来,最开始还以为是业务逻辑限制了不能点击。后来才发现别人的电脑可以点出来,老版本的浏览器也可以点出来,最后定位到是新版的chrome就不行了 这是我的浏览器版本…...

beanDefinition读取器
编程式定义 BeanDefinition:自定义一个BeanDefinition, AbstractBeanDefinition beanDefinition BeanDefinitionBuilder.genericBeanDefinition().getBeanDefinition(); 设置beanClass 注册到容器中 B…...
linux 上flink单机安装详解
目录 一 准备安装包 二 解压 三 配置环境变量 四 验证是否部署成功 一 准备安装包 官网地址: Downloads | Apache Flink 百度网盘资源: 链接: https://pan.baidu.com/s/15aXmF3JLxnOlPiDxId637Q?pwdsqsx 提取码: sqsx 这里准备的版本是flink1.13…...
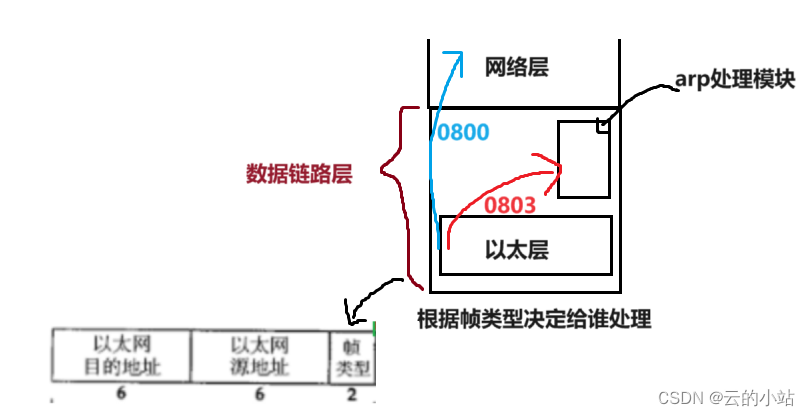
数据链路层中存在的报文ip,arp,rarp
IP数据报 ARP请求/应答报 RARP请求/应答报 IP数据报 这里的目的地址和源地址是MAC地址。 这个被称为 MAC 地址,是一个网卡的物理地址,用十六进制,6 个 byte 表示。 MAC 地址是一个很容易让人误解的地址。因为 MAC 地址号称全球唯一&…...

【Tricks】PC端微信输入时,文本出现右对齐情况怎么恢复
应该是摁到某个快捷键,于是光标就变成如下图所示的样子: 如果再输入字符,则字符就会变成下图所示的样子(对齐输入框右侧): 解决办法:ctrl J 解决办法:ctrl J 解决办法࿱…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
