算法---缺失的第一个正数
题目
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。示例 1:输入:nums = [1,2,0]
输出:3
示例 2:输入:nums = [3,4,-1,1]
输出:2
示例 3:输入:nums = [7,8,9,11,12]
输出:1提示:1 <= nums.length <= 5 * 105
-231 <= nums[i] <= 231 - 1
解决思路
借用map 就可以实现,但是如果不借用map,在原空间上,也可以实现,不过想要使用原来的数据,会有侵略性,会把原来的数据修改掉。
解决方法
方法一:
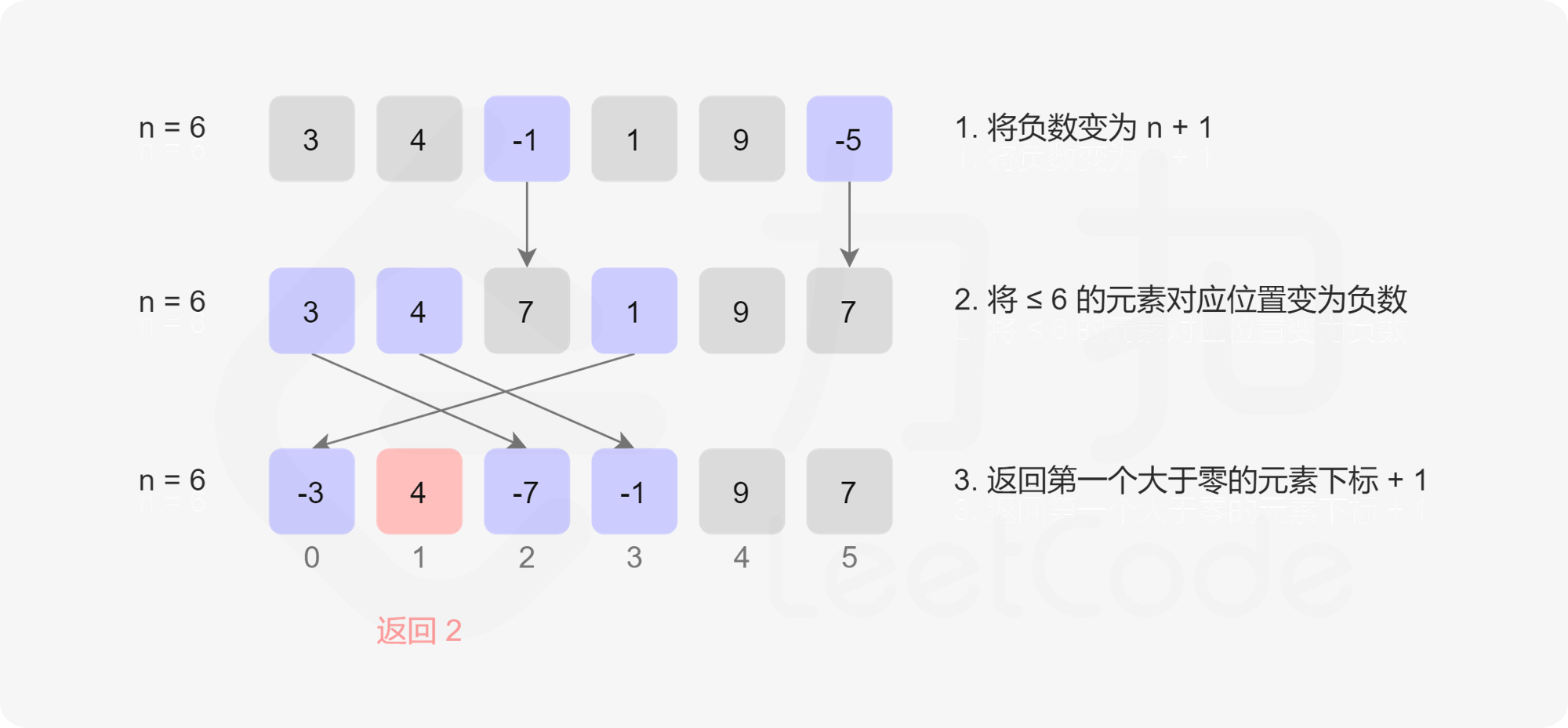
fun firstMissingPositive(nums: IntArray): Int {val size = nums.sizenums.forEachIndexed { index, i ->if (i <= 0) {nums[index] = size + 1}}nums.forEachIndexed { index, i ->if (i.absoluteValue in 1..size && nums[i.absoluteValue -1] > 0) {nums[i.absoluteValue -1] = -nums[i.absoluteValue -1]}}nums.forEachIndexed { index, i ->if (i >= 0){return index + 1}}return size + 1}
方法二:
fun firstMissingPositive2(nums: IntArray): Int {val size = nums.sizevar temp = 0nums.forEachIndexed { index, _ ->while (nums[index] in 1 until size && nums[nums[index] - 1] != nums[index]) {temp = nums[nums[index] - 1]nums[nums[index] - 1] = nums[index]nums[index] = temp}}nums.forEachIndexed { index, i ->if (index != i - 1) {return index + 1}}return size + 1}
总结
算法是很看一个人的思维逻辑的,所以很多都会考验一下算法。
算法确实重要。
做了快一年算法了,确实 学习如园中小草,不见其增,日有所长
面试遇到算法就很轻松就过了
相关文章:

算法---缺失的第一个正数
题目 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。示例 1:输入:nums [1,2,0] 输出:3 示例 2:输入:nums …...

【算法与数据结构】--算法应用--算法和数据结构的案例研究
一、项目管理中的算法应用 在项目管理中,算法和数据结构的应用涉及项目进度、资源分配、风险管理等方面。以下是一些案例研究,展示了算法在项目管理中的实际应用: 项目进度管理: 甘特图算法:甘特图是一种项目进度管理…...

java如何获取调用接口的ip?
获取调用者的ip 场景:想知道哪个ip访问的某个接口时,就需要打印出来看看,这时就可以使用这个方法了。 案例: //HttpServletRequest 入参加上,请求对象public ForkResponse queryXXX(RequestBody XXXX xxxx, HttpServletRequest …...

ubuntu 18 更新git版本到 2.80.1
前言 使用gitlab的时候,发现下面这条语句不能用 git init --initial-branch XXX查看git version git version下载 wget https://mirrors.edge.kernel.org/pub/software/scm/git/git-2.38.1.tar.gz 或者 https://git-scm.com/download/linux 或者去github上面下载…...
测试C#调用Aplayer播放视频(2:VideoPlayer源码学习)
参考文献1除了介绍Aplayer组件的用法之外,还提供有demo下载以供学习,本文学习并记录其中的使用方式。 VideoPlayer项目使用C#在VS2013开发,其解决方案中包括VideoPlayer和VideoPlayer两个小项目,前者基于.net framework4.0&am…...

YOLOv5 分类模型的预处理
YOLOv5 分类模型的预处理 flyfish 版本 6.2 将整个代码简化成如下代码 imgsz224 file "/home/a/Pictures/1.jpg" transforms classify_transforms(imgsz) im cv2.cvtColor(cv2.imread(file), cv2.COLOR_BGR2RGB) print(im.shape)im transforms(im) print(im.…...

25 行为型模式-备忘录模式
1 备忘录模式介绍 备忘录模式(memento pattern)定义: 在不破坏封装的前提下,捕获一个对象的内部状态,并在该对象之外保存这个状态,这样可以在以后将对象恢复到原先保存的状态. 2 备忘录模式原理 3 备忘录模式实现 /*** 发起人角色**/ public class Originator {private Strin…...

物联网AI MicroPython传感器学习 之 SHT3X温湿度传感器
学物联网,来万物简单IoT物联网!! 一、产品简介 Sensirion SHT3x-DIS湿度和温度传感器基于CMOSens传感器芯片,更加智能、可靠,精度更高。SHT3x-DIS具有增强的信号处理能力、两个独特的用户可选I2C地址,通信…...
;delete[] p; delete p;区别是什么?)
int* p = new int[5]; int *p = new int[5]();delete[] p; delete p;区别是什么?
int main() {int *p new int[5]; // 分配包含5个整数的数组内存// 初始化数组元素for (int i 0; i < 5; i) {p[i] i * 10;}// 试图使用 delete p; 来释放数组内存delete p;delete[] p;// 打印数组元素for (int i 0; i < 5; i) {std::cout << "p[" &l…...

数据结构|基础知识定义
1.值传递、地址传递、值返回、地址返回 1> 值传递:普通变量作为函数参数传递是单向的值传递,只是将实参的值复制一份给形参变量,形参的改变不会影响实参的值,因为所在内存空间不同 如果传递的是地址,被调函数使用指…...

物联网AI MicroPython传感器学习 之 MFRC522 RFID射频IC卡感应模块
学物联网,来万物简单IoT物联网!! 一、产品简介 MFRC522是应用于13.56MHz非接触式通信中高集成度的读写卡芯片,其特点低电压、低成本、体积小的非接触式读写芯片。MFRC522支持MIFARE系列更高速的非接触式通信,双向数据…...
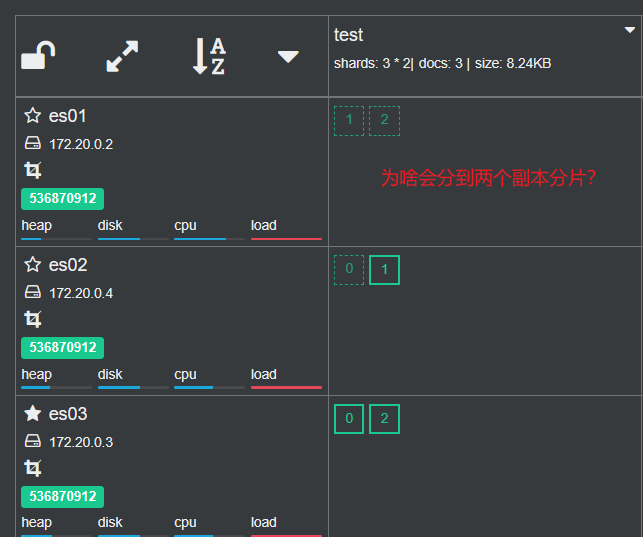
搭建ES集群
目录 前言 搭建ES集群 集群状态监控 分片备份 节点角色 脑裂问题 分布式存储 分布式查询 故障转移 前言 单机的ES做数据存储必然会面临两个问题:海量数据存储问题、单机故障问题 海量数据存储问题:将索引库从逻辑上拆分为N个分片(shard)&…...

Tomcat的日志接收文件catalina.out nohup.out说明
catalina.out用于接收如下情况的日志: catalina.out其实是tomcat的标准输出(stdout)和标准出错(stderr),这是在tomcat的启动脚本里指定的,如果没有修改的话stdout和stderr会重定向到这里。所以我们在应用里使用System.out打印的东西都会到这…...

手机ip地址切换后有什么影响
随着互联网的普及和人们对网络连接的需求不断增加,手机已经成为我们日常生活中不可或缺的一部分。而在使用手机的过程中,手机ip地址的切换也成为了许多用户需要注意的问题。虎观代理小二二将探讨手机ip地址切换后可能产生的影响。 手机ip地址的含义及作…...
C++ 赋值运算重载,const成员,取地址及const取地址操作符重载
C 赋值运算重载,const成员,取地址及const取地址操作符重载 1. 赋值运算符重载1.1 运算符重载1.2 赋值运算符重载1.3 前置/--和后置/--重载 2. const成员3. 取地址及const取地址操作符重载 所属专栏:C“嘎嘎" 系统学习❤️ 🚀…...
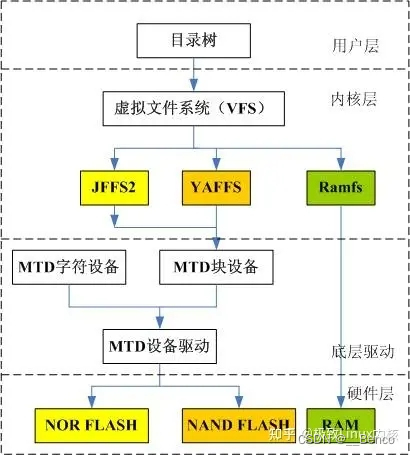
嵌入式Linux系统的闪存设备和文件系统学习纪要
嵌入式Linux系统的闪存设备和文件系统学习纪要 Linux下的文件系统结构如下: NAND Flash 是一种非易失性存储器(Non-Volatile Memory),常用于闪存设备和固态硬盘(SSD)中。以下是几种常见的 NAND Flash 种类&…...
android 8.1 disable unsupported sensor
如果device不支持某种sensor,可以在android/frameworks/base/core/java/android/hardware/SystemSensorManager.java里将其disabled掉。以disable proximity sensor为例。 public SystemSensorManager(Context context, Looper mainLooper) {synchronized(sLock) {if (!sNativ…...

二、类与对象(一)
1 面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解决问题。以洗衣服为例,通常洗衣服会经历以下过程: 而C是基于面向对象的,关注的是对象,…...

写给所有的程序员,或者努力生活的你。
朋友们,好好休息,意味着好好锻炼,好好睡觉,好好学习,学习可以是功利的,需要有规划的,有执行能力,有反馈奖励机制的,也可以无用之用方为大用(比如take shit的时…...
pytorch 笔记:GRU
1 介绍 对于输入序列中的每个元素,每一层都计算以下函数: ht 是t时刻 的隐藏状态xt 是t时刻 的输入ht−1 是 t-1时刻 同层的隐藏状态或 0时刻 的初始隐藏状态rt,zt,nt 分别是重置门、更新门和新门。σ 是 sigmoid 函数∗ 是 Hadamard 乘积。…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
