【人工智能Ⅰ】5-粒子群算法
【人工智能Ⅰ】5-粒子群算法
文章目录
- 【人工智能Ⅰ】5-粒子群算法
- 5.1 粒子群算法PSO基本思想
- 5.2 PSO介绍
- 5.3 PSO求最优解
- 5.4 算法流程
- 5.5 PSO构成要素
- 群体大小m
- 权重因子
- 最大速度Vm
- 停止准则
- 粒子空间的初始化
- 领域的拓扑结构
- 5.6 PSO应用
- 5.7 PSO改进
- 动态调整惯性权重
- 收缩因子法
- 5.8 群智能优化的特点和不足
- 共同特点
- 存在问题
- 进一步研究
- 5.9 群智能小结
5.1 粒子群算法PSO基本思想
特点:简单、收敛速度快、设置参数少
群体迭代,粒子在解空间追随最优的粒子进行搜索
PSO基础:信息的社会共享
粒子群特性:社会行为 + 个体认知
5.2 PSO介绍
1:所有粒子都在一个D维空间搜索
2:所有粒子由适应度函数确定适应值,用于判断目前位置的好坏
3:所有粒子有记忆功能,保存最佳位置
4:所有粒子以一个速度决定飞行距离和方向,且速度根据个体认知和社会行为进行动态调整
5.3 PSO求最优解
D维空间,N个粒子
粒子i位置:(可将x_i带入适应度函数f(x)求解适应值)
x i = ( x i 1 , . . . , x i D ) x_i=(x_{i1},...,x_{iD}) xi=(xi1,...,xiD)
粒子i速度:
v i = ( v i 1 , . . . , v i D ) v_i=(v_{i1},...,v_{iD}) vi=(vi1,...,viD)
粒子i的最好位置:
p b e s t i = ( p i 1 , . . . , p i D ) pbest_i=(p_{i1},...,p_{iD}) pbesti=(pi1,...,piD)
种群的最好位置:
g b e s t = ( g 1 , . . . , g D ) gbest=(g_1,...,g_D) gbest=(g1,...,gD)
在第d维的位置变化范围:
[ X m i n , d , X m a x , d ] [X_{min,d},X_{max,d}] [Xmin,d,Xmax,d]
在第d维的速度变化范围:
[ − V m a x , d , V m a x , d ] [-V_{max,d},V_{max,d}] [−Vmax,d,Vmax,d]
上述范围保证了位置和速度约束在预设的边界内部
粒子i在第d维的速度更新:
v i d k = w v i d k + c 1 r 1 ( p b e s t i d − x i d k − 1 ) + c 2 r 2 ( g b e s t d − x i d k − 1 ) v_{id}^k=wv_{id}^k+c_1r_1(pbest_{id}-x_{id}^{k-1})+c_2r_2(gbest_{d}-x_{id}^{k-1}) vidk=wvidk+c1r1(pbestid−xidk−1)+c2r2(gbestd−xidk−1)
粒子i在第d维的位置更新:
x i d k = x i d k − 1 + v i d k − 1 x_{id}^k=x_{id}^{k-1}+v_{id}^{k-1} xidk=xidk−1+vidk−1
c1、c2:加速度常数,调节学习最大步长
r1、r2:随机函数,取值范围[0,1],增加搜索随机性
w:惯性权重,非负,调节搜索范围
粒子的速度更新包括三部分:
1:粒子先前的速度
w v k wv_k wvk
2:认知:粒子当前位置与自己最好位置间的距离
c 1 r 1 ( p b e s t i d − x i d k − 1 ) c_1r_1(pbest_{id}-x_{id}^{k-1}) c1r1(pbestid−xidk−1)
3:社会:粒子当前位置与群体最好位置间的距离
c 2 r 2 ( g b e s t d − x i d k − 1 ) c_2r_2(gbest_{d}-x_{id}^{k-1}) c2r2(gbestd−xidk−1)
5.4 算法流程
1:初始化
初始化群体规模未n,以及随机位置和速度
2:评估
根据适应度函数,评价每个粒子的适应度
3:找到个体最优pbest
比较当前适应度值和个体pbest,更新pbest
4:找到群体最优gbest
比较当前适应度值和群体gbest,更新gbest
5:更新粒子情况
根据公式更新每个粒子的速度和位置
6:终止
如果达到最大迭代次数G_max,或最佳适应度值的增量小于阈值
5.5 PSO构成要素
群体大小m
过小:提前局部最优
过大:优化能力好但收敛速度慢,当群体数目增长到一定水平时,再增长不明显
权重因子
1:惯性因子w
若w=1,则是基本粒子群算法
若w=0,则失去对粒子本身速度的记忆
2:学习因子c1、c2
若c1=0,则是无私型粒子,会丧失群体多样性,陷入局部最优解
若c2=0,则是自我认知型粒子,会丧失信息社会共享,收敛速度缓慢
若c1!=0且c2!=0,则是完全型粒子,平衡收敛速度和搜索效率
最大速度Vm
作用:维护探索能力和开发能力的平衡
过大:探索能力增强,但容易飞过全局最优解
过小:开发能力增加,但容易陷入局部最优解
一般变化范围:每个维度变量的10%-20%
停止准则
1:最大迭代步数
2:可接受的满意解
粒子空间的初始化
依赖于问题
特色:参数少,惯性因子和领域定义重要
领域的拓扑结构
1:群体内所有个体都是粒子的领域(对应全局粒子群算法)
2:群体内部分个体是粒子的领域(对应局部粒子群算法)
领域拓扑结构,决定,群体pbest
邻域随迭代次数的增加线性变大,最后邻域扩展到整个粒子群
全局粒子群算法:收敛速度快,容易局部最优
局部粒子群算法:收敛速度慢,不容易局部最优
5.6 PSO应用
1:函数优化问题
2:TSP问题(路径对应位置,交换子/交换序列对应速度)
3:参数优化
4:组合优化
5.7 PSO改进
动态调整惯性权重
前期提高全局搜索能力(w较大),找到合适的种子
后期提高局部搜索能力(w较小),提高收敛精度
解决方法:线性递减权值
w = w m a x − ( w m a x − w m i n ) ∗ r u n / r u n m a x w=w_{max}-(w_{max}-w_{min})*run/run_{max} w=wmax−(wmax−wmin)∗run/runmax
w m a x :最大惯性权重, w m i n :最小惯性权重, r u n :当前迭代次数, r u n m a x :总迭代次数 w_{max}:最大惯性权重,w_{min}:最小惯性权重,run:当前迭代次数,run_{max}:总迭代次数 wmax:最大惯性权重,wmin:最小惯性权重,run:当前迭代次数,runmax:总迭代次数
收缩因子法
作用:保证收敛性
速度更新公式:
v i d = K [ v i d + f 1 r 1 ( p b e s t i d − x i d ) + f 2 r 2 ( g b e s t d − x i d ) ] v_{id}=K[v_{id}+f_1r_1(pbest_{id}-x_{id})+f_2r_2(gbest_{d}-x_{id})] vid=K[vid+f1r1(pbestid−xid)+f2r2(gbestd−xid)]
K :收缩因子(受到 f 1 和 f 2 限制的 w ), f 1 和 f 2 是预先设定的模型参数 K:收缩因子(受到f_1和f_2限制的w),f_1和f_2是预先设定的模型参数 K:收缩因子(受到f1和f2限制的w),f1和f2是预先设定的模型参数
K = 2 / ∣ 2 − f − t ( f 2 − 4 f ) ∣ K=2/|2-f-\sqrt{t(f^2-4f)}| K=2/∣2−f−t(f2−4f)∣
f = f 1 + f 2 , f > 4 f=f_1+f_2,f>4 f=f1+f2,f>4
5.8 群智能优化的特点和不足
共同特点
基于概率计算的随机搜索进化算法,在结构、研究内容、方法以及步骤上有较大的相似性
存在问题
1:数学理论基础相对薄弱
2:参数设置没有确切的理论依据,对具体问题和应用环境的依赖性大;
3:比较性研究不足,缺乏用于性能评估的标准测试集;
4:不具备绝对的可信性,存在应用风险
进一步研究
1:真实群居动物的行为特征
2:算法收敛性
3:提高收敛速度,从而解决大规模优化问题
4:各种参数设置问题
5:群智能的并行算法
6:各算法的适用范围
7:与其它算法的混合技术
5.9 群智能小结
1:什么是群?什么是群智能?
2:群智能算法的一般框架
3:群智能算法有哪些?
4:PSO的基本思想,粒子、评价函数、粒子学习(跟踪2个极值:个体极值和社会极值)
5:粒子的速度更新公式的含义,各部分对算法性能的作用
6:PSO算法步骤
相关文章:

【人工智能Ⅰ】5-粒子群算法
【人工智能Ⅰ】5-粒子群算法 文章目录 【人工智能Ⅰ】5-粒子群算法5.1 粒子群算法PSO基本思想5.2 PSO介绍5.3 PSO求最优解5.4 算法流程5.5 PSO构成要素群体大小m权重因子最大速度Vm停止准则粒子空间的初始化领域的拓扑结构 5.6 PSO应用5.7 PSO改进动态调整惯性权重收缩因子法 5…...

软考高项-49个项目管理过程输入、输出和工具技术表
知识领域数量五大过程组启动规划执行监控收尾整体7制订项目章程制订项目管理计划指导与管理项目工作 管理项目知识 监控项目工作 实施整体变更控制 结束项目或阶段范围6规划范围管理 收集需求 定义范围 创建WBS 确认范围 控制范围 进度6规划进度管理 定义活动...

《C和指针》(7)函数
问题 具有空函数体的函数可以作为存根使用。你如何对这类函数进行修改,使其更加有用? 答:当存根函数被调用时,打印一条消息,显示它已被调用,或者也可以打印作为参数传递给它的值。 .如果在一个函数的声明中…...

vue3中的Props
Props声明 一个组件需要显示声明它所接受的props,这样vue才能知道外部传入的哪些是props,哪些是透传attribute 在使script setup的单文件中,props可以使用 defineProps()宏来声明: <script setup> const props definePro…...
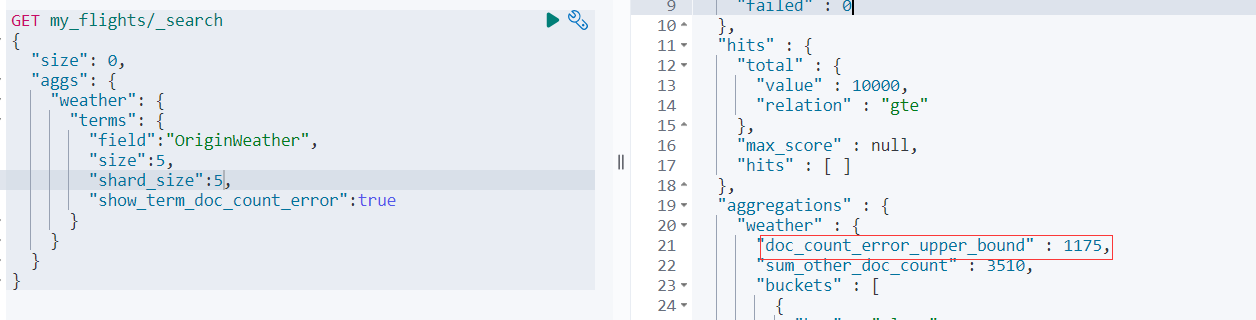
ElasticSearch搜索技术深入与聚合查询实战
ES分词器详解 基本概念 分词器官方称之为文本分析器,顾名思义,是对文本进行分析处理的一种手段,基本处理逻辑为按照预先制定的分词规则,把原始文档分割成若干更小粒度的词项,粒度大小取决于分词器规则。 分词发生时…...

vue+element ui中的el-button自定义icon图标
实现 button的icon属性自定义一个图标名称,这个自定义的图标名称会默认添加到button下i标签的class上,我们只需要设置i标签的样式就可以了 ##3. 按钮上使用自定义的icon 完整代码 <div class"lookBtn"><el-button icon"el-icon-…...

PyQt5:构建目标检测算法GUI界面 (附python代码)
文章目录 1.界面2.代码3.Analyze 1.界面 目标检测算法一般就是检测个图片,然后显示图片结果。 最简单的情况,我们需要一个按钮读取图片,然后后有一个地方显示图片。 2.代码 import sys import numpy as np from PIL import Imagefrom PyQt…...
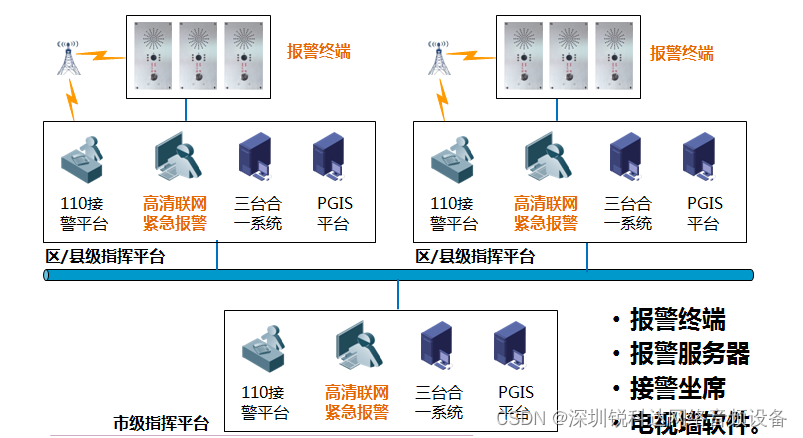
SV-10A-4G IP网络报警非可视终端 (4G版)
SV-10A-4G IP网络报警非可视终端 (4G版) https://item.taobao.com/item.htm?spma21dvs.23580594.0.0.621e3d0dpv5knb&ftt&id745728046948 产品简介: 通过局域网/广域网网组网的网络报警系统,改变传统局域网组网…...

对xml文本元素赋值
public static void main(String[] args) {Map map ....;//数据Iterator it doc.getRootElement().elementIterator();//doc是xml模板//将元素ID与输入框的值放在map中while (it.hasNext()) {org.dom4j.Element nextRoot (org.dom4j.Element) it.next();Iterator nextIt ne…...

【k8s】资源管理命令-陈述式
一、资源管理介绍 1、资源管理概念 在kubernetes中,所有的内容都抽象为资源,用户需要通过操作资源来管理kubernetes。 //kubernetes的本质就是一个集群系统,用户可以在集群中部署各种服务,起始就是在kubernetes集群中运行一个个…...
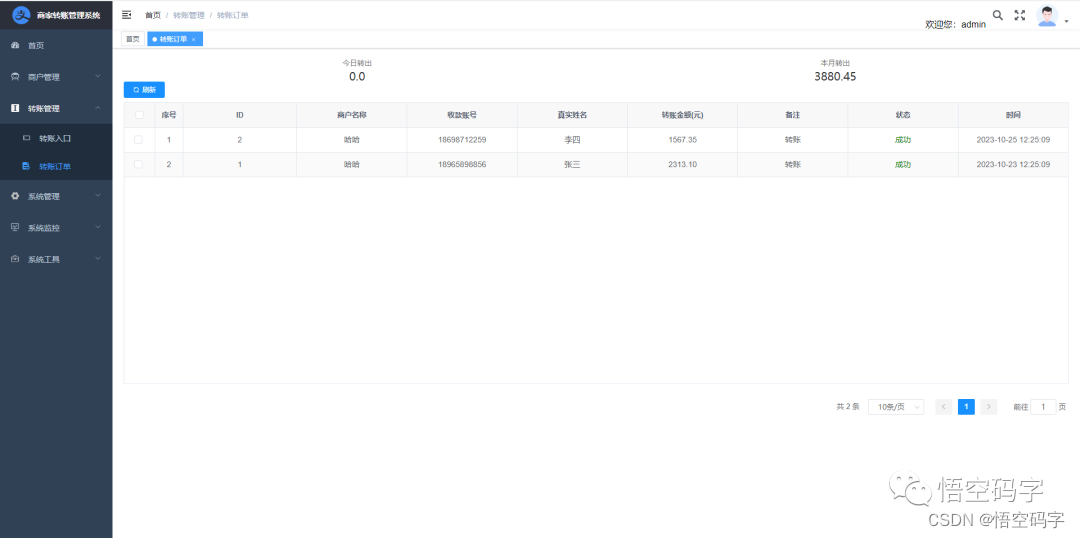
无需频繁登录支付宝网站即可完成商家转账,实时到账,方便安全快捷
大家好,我是小悟 转账到支付宝账户是一种通过 API 完成单笔转账的功能,支付宝商家可以向其他支付宝账户进行单笔转账。 商家只需输入另一个正确的支付宝账号,即可将资金从本企业支付宝账户转账至另一个支付宝账户。 该产品适用行业较广&am…...
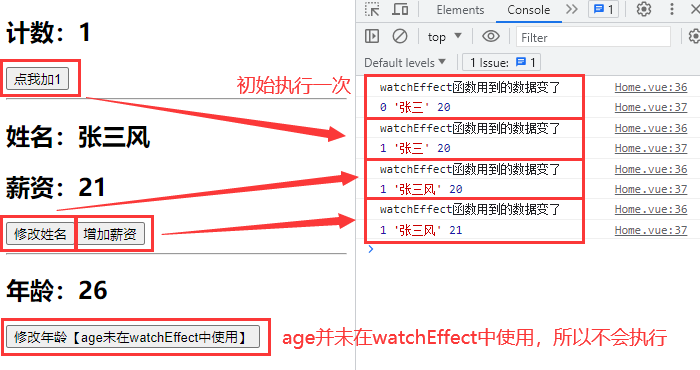
Vue 监听属性 watchEffect
watchEffect 函数:自动收集依赖源,不用指定监听哪个数据,在监听的回调中用到哪个数据,就监听哪个数据。 而 watch 函数:既要指定监听的数据,也要指定监听的回调。 watchEffect 函数:类似于 co…...

设计模式: 关于项目架构,技术选型,技术债务问题与解决方案
正确的选择是良好的开端 1 )指标 系统稳健性系统健壮性 2 ) 衡量 在概念层次衡量架构质量在实际开发中衡量架构好坏 3 ) 架构分类 系统架构 从系统维度,负责整体系统的架构设计基础服务和各系统间协调,着眼全局比如关注负载,…...

el-tabs 默认选中第一个
1. 实际开发中el-tabs 都会设置第一个为默认值 ,这样会好看一点, 而渲染的数据经常是通过后端返回的数据 , v-model 无法写死默认值 解决办法 , 通过计算机属性 ,在data 定义一个 selectedTab watch: {defaultTab(newVal) {this.selectedTab newVal; // 设置第一个标签页…...

R -- match,pmatch,charmatch
文章目录 matchpmatchcharmatch match ?matchDescription match returns a vector of the positions of (first) matches of its first argument in its second. 第一个向量中的元素在第二个向量中的位置,如果第二个向量中有多个仅返回第一个match 元素的位置&…...

数据结构——线性表①(顺序表)
一、线性表定义 线性表是一种数据结构,它是由n个具有相同数据类型的数据元素a1,a2,…,an组成的有限序列。 其中,除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an外,每一个元素有且只有一个…...
MFC网络编程-Udp客户端
目录 1、UI的设计: 2、代码的实现: (1)、重写CSocket虚函数OnReceive,并且传入对话框的指针 (2)、初始化SOCKET (3)、绑定本地IP和端口 (4)、…...

密码学基础
密码学总览 信息安全面临的危险与应对这些威胁的密码技术: 关于上图中的威胁,这里在简单的说明: 窃听:指的是需要保密的消息被第三方获取。篡改:指的是消息的内容被第三方修改,达到欺骗的效果。伪装&…...

[Docker]四.Docker部署nodejs项目,部署Mysql,部署Redis,部署Mongodb
一.部署nodejs项目,映射端口,挂载数据卷 可以到https://hub.docker.com/去搜索node镜像,然后下载,也可以直接通过docker pull node下载镜像,然后用这个node镜像启动容器node,这样系统就集成了node服务了,在这里挂载www/node目录到容器中,并指定端口映射,运行nodejs程序,安装npm…...

拥抱AI-ChatGPT:人类新纪元
最近大模型通用智能应用持续发酵,各大科技公司都陆续推出了基于通用大模型的智能应用产品,典型的如OpenAI的ChatGPT、微软的BingChat、百度的文心一言、360的智脑、阿里的通义千问等。当然最火的要属于ChatGPT了,从去年年底推出到现在已经有很…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
