灰狼优化算法(GWO)python
目录
一、灰狼优化算法的python实现
二、灰狼优化算法与遗传算法的对比分析(python)
2.1 GWO1.py
2.2 GA1.py
2.3 GWO_vs_GA.py
2.4 运行结果
三、基于莱维飞行改进的灰狼优化算法的python实现
一、灰狼优化算法的python实现
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False'''定义函数'''
def function(X0):''':param X0: x的取值:param dim: 维度:return: 函数值'''s=0s=1/(1+np.abs(X0[0])+np.abs(X0[1])+np.abs(X0[2])+np.abs(X0[3]))return s'''灰狼优化算法——GWO'''
def GWO(NP,dim,NG,amax,x_max,x_min):''':param NP:种群规模:param dim: 数据维度:param NG: 最大迭代步数:param amax: 系数向量初始值:param x_max: 解允许的最大值:param x_min: 解允许的最小值:return: 最优解的目标函数值''''''随机产生初始解'''X0=np.zeros((NP,dim))value0=[] #函数值for i in range(NP):X0[i]=np.random.uniform(low=x_min,high=x_max,size=(1, dim))value0.append(function(X0[i]))'''存储历史最优解和历史最优函数值'''X_best=[] #历史最优解value_best=[] #历史最优函数值'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''#得到对目标函数值列表value0升序排列后的索引index_sort=np.argsort(np.array(value0))#对value0进行降序排列value0_sort=[value0[i] for i in index_sort[::-1]]#对X0进行相应的排列X0_sort=[X0[i] for i in index_sort[::-1]]'''得到初始解的最优解和最优函数值'''X_best.append(X0_sort[0])value_best.append(value0_sort[0])print("--------------------灰狼优化算法--------------------")print("初始最优解:\n{}".format(X_best[0].tolist()))print("初始最优函数值:\n{}".format(value_best[0]))'''选出最优的三个个体,并获得它们的位置信息'''Xalpha=X0_sort[0]Xbeta=X0_sort[1]Xdelta=X0_sort[2]'''开始利用灰狼优化算法进行训练'''for i in range(NG):'''计算系数向量的参数a'''ratio=i/NGa=amax*(1-ratio)'''对每个个体的位置进行更新'''for j in range(NP):'''分别计算在函数值最优的前三个个体的影响下,个体的位置移动量X1、X2、X3'''C1=2*np.random.rand()Dalpha=np.abs(C1*Xalpha-X0[j])A1=2*a*np.random.rand()-aX1=Xalpha-A1*DalphaC2=2*np.random.rand()Dbeta=np.abs(C2*Xbeta-X0[j])A2=2*a*np.random.rand()-aX2=Xbeta-A2*DbetaC3=2*np.random.rand()Ddelta=np.abs(C3*Xdelta-X0[j])A3=2*a*np.random.rand()-aX3=Xdelta-A3*Ddelta'''计算个体移动后的位置及函数值'''X0[j]=(X1+X2+X3)/3value0[j]=function(X0[j])'''对种群历史最优解和历史最优函数值进行更新'''if max(value0)>max(value_best):value_best.append(max(value0))X_best.append(X0[value0.index(max(value0))])else:value_best.append(value_best[-1])X_best.append(X_best[-1])'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''#得到对目标函数值列表value0升序排列后的索引index_sort=np.argsort(np.array(value0))#对X0进行相应的降序排列X0_sort=[X0[i] for i in index_sort[::-1]]'''选出最优的三个个体,并获得它们的位置信息'''Xalpha=X0_sort[0]Xbeta=X0_sort[1]Xdelta=X0_sort[2]'''返回最优解和最优函数值'''return X_best,value_best
二、灰狼优化算法与遗传算法的对比分析(python)
2.1 GWO1.py
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False'''定义函数'''
def function(X0):''':param X0: x的取值:param dim: 维度:return: 函数值'''s=0s=1/(1+np.abs(X0[0])+np.abs(X0[1])+np.abs(X0[2])+np.abs(X0[3]))return s'''灰狼优化算法——GWO'''
def GWO(NP,dim,NG,amax,x_max,x_min):''':param NP:种群规模:param dim: 数据维度:param NG: 最大迭代步数:param amax: 系数向量初始值:param x_max: 解允许的最大值:param x_min: 解允许的最小值:return: 最优解的目标函数值''''''随机产生初始解'''X0=np.zeros((NP,dim))value0=[] #函数值for i in range(NP):X0[i]=np.random.uniform(low=x_min,high=x_max,size=(1, dim))value0.append(function(X0[i]))'''存储历史最优解和历史最优函数值'''X_best=[] #历史最优解value_best=[] #历史最优函数值'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''#得到对目标函数值列表value0升序排列后的索引index_sort=np.argsort(np.array(value0))#对value0进行降序排列value0_sort=[value0[i] for i in index_sort[::-1]]#对X0进行相应的排列X0_sort=[X0[i] for i in index_sort[::-1]]'''得到初始解的最优解和最优函数值'''X_best.append(X0_sort[0])value_best.append(value0_sort[0])print("--------------------灰狼优化算法--------------------")print("初始最优解:\n{}".format(X_best[0].tolist()))print("初始最优函数值:\n{}".format(value_best[0]))'''选出最优的三个个体,并获得它们的位置信息'''Xalpha=X0_sort[0]Xbeta=X0_sort[1]Xdelta=X0_sort[2]'''开始利用灰狼优化算法进行训练'''for i in range(NG):'''计算系数向量的参数a'''ratio=i/NGa=amax*(1-ratio)'''对每个个体的位置进行更新'''for j in range(NP):'''分别计算在函数值最优的前三个个体的影响下,个体的位置移动量X1、X2、X3'''C1=2*np.random.rand()Dalpha=np.abs(C1*Xalpha-X0[j])A1=2*a*np.random.rand()-aX1=Xalpha-A1*DalphaC2=2*np.random.rand()Dbeta=np.abs(C2*Xbeta-X0[j])A2=2*a*np.random.rand()-aX2=Xbeta-A2*DbetaC3=2*np.random.rand()Ddelta=np.abs(C3*Xdelta-X0[j])A3=2*a*np.random.rand()-aX3=Xdelta-A3*Ddelta'''计算个体移动后的位置及函数值'''X0[j]=(X1+X2+X3)/3value0[j]=function(X0[j])'''对种群历史最优解和历史最优函数值进行更新'''if max(value0)>max(value_best):value_best.append(max(value0))X_best.append(X0[value0.index(max(value0))])else:value_best.append(value_best[-1])X_best.append(X_best[-1])'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''#得到对目标函数值列表value0升序排列后的索引index_sort=np.argsort(np.array(value0))#对X0进行相应的降序排列X0_sort=[X0[i] for i in index_sort[::-1]]'''选出最优的三个个体,并获得它们的位置信息'''Xalpha=X0_sort[0]Xbeta=X0_sort[1]Xdelta=X0_sort[2]'''返回最优解和最优函数值'''return X_best,value_best
2.2 GA1.py
import random
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False'''产生初始种群'''
def initialpopulation(NP,n,x0,x1):'''NP代表种群规模,n代表目标函数的未知量的个数;x0代表未知数取值的下限,x1代表未知数取值的上限'''initial=[]for i in range(NP):n_initial=[random.uniform(x0,x1) for j in range(n)]initial.append(n_initial)return initial'''标定适值函数'''
def fitnessfunction(X):'''X代表存储各个未知量的取值的列表'''return 1/(math.sqrt(X[0]**2)+math.sqrt(X[1]**2)+math.sqrt(X[2]**2)+math.sqrt(X[3]**2)+1)'''采用轮盘赌选择算法选择个体'''
def selection(NP,X0):'''NP代表种群规模,X0代表种群'''#计算种群中各个个体的适应值value=[]for i in range(NP):value.append(fitnessfunction(X0[i]))'''计算适应度和累计概率函数'''#计算选择概率fsum=0for i in range(NP):fsum=fsum+value[i]**2value_ratio=[]for i in range(NP):value_ratio.append((value[i]**2)/fsum)#计算累加概率value_ratio_add=[]for i in range(NP):if i==0:value_ratio_add.append(value_ratio[i])else:value_ratio_add.append(value_ratio_add[i-1]+value_ratio[i])#产生[0,1]之间的随机数,进行NP次轮转random_ratio=[random.uniform(0,1) for i in range(NP)]#进行轮盘赌选择choose_index=[] #从0开始计value_ratio_add0=[0,*value_ratio_add] #在列表value_ratio_add的最前面加上一个0for i in range(NP):for j in range(NP):if random_ratio[i]>=value_ratio_add0[j] and random_ratio[i]<value_ratio_add0[j+1]:choose_index.append(j)break#得到经过轮盘赌选择算法后的种群population=[X0[i] for i in choose_index]return population'''遗传运算——双切点交叉'''
def crossover1(X0,pc,NP,n):'''X0代表种群,pc代表交叉概率,NP代表种群规模,n代表染色体上的基因数目'''# 对每个染色体生成一个[0,1]之间的随机数random_crossover=[random.uniform(0, 1) for i in range(NP)]# 判断哪些染色体进行交叉运算crossover_index=[] # 种群中进行交叉运算的染色体的索引值for i in range(NP):if random_crossover[i]<pc:crossover_index.append(i)# 判断初步确定的需要交叉的染色体个数,如果为奇数,则最后一个染色体不进行交叉运算if (len(crossover_index)%2)!=0:crossover_index.pop()crossover_index=crossover_index#进行双切点交叉if len(crossover_index)!=0:randint_index=[sorted(random.sample([i for i in range(0,n-1)],2)) for i in range(int(len(crossover_index)/2))]for i in range(0,len(crossover_index),2):crossover1=X0[crossover_index[i]]crossover2=X0[crossover_index[i+1]]crossoverindex=randint_index[int(i/2)]#分割crossover1_1=[crossover1[j] for j in range(crossoverindex[0]+1)]crossover1_2=[crossover1[j] for j in range(crossoverindex[0]+1,crossoverindex[1]+1)]crossover1_3=[crossover1[j] for j in range(crossoverindex[1]+1,n)]crossover2_1=[crossover2[j] for j in range(crossoverindex[0]+1)]crossover2_2=[crossover2[j] for j in range(crossoverindex[0]+1,crossoverindex[1]+1)]crossover2_3=[crossover2[j] for j in range(crossoverindex[1]+1,n)]#交换X0[crossover_index[i]]=[*crossover1_1,*crossover2_2,*crossover1_3]X0[crossover_index[i+1]]=[*crossover2_1,*crossover1_2,*crossover2_3]#返回进行双切点交叉后的种群return X0'''进行遗传运算——变异'''
def mutation(X0,pm,NP,n,x0,x1):'''X0代表种群,pm代表交叉概率,NP代表种群规模,n代表染色体上的基因数目x0代表未知数取值的下限,x1代表未知数取值的上限'''#生成在[0,1]上的随机数列表random_gene=[[random.uniform(0,1) for i in range(n)] for j in range(NP)]#进行变异运算for i in range(NP):for j in range(n):if random_gene[i][j]<pm:X0[i][j]=random.uniform(x0,x1)#返回经过变异操作后的种群return X0'''计算种群中所有个体的适应值并返回最大值'''
def fitnessmax(X0,NP):'''X0代表种群,NP代表种群规模'''#计算种群中各个个体的适应值value=[]for i in range(NP):value.append(fitnessfunction(X0[i]))value_max=max(value)#适应值最大所对应的索引值index_max=value.index(max(value))#适应值最大所对应的染色体X0_max=X0[index_max]return value_max,X0_max'''使用双切点交叉的遗传算法'''
def GA1(NP,NG,n,x0,x1,pc,pm):'''NP代表种群规模,NG代表最大代数,n代表一个染色体的基因数x0代表未知数取值的下限,x1代表未知数取值的上限pc代表交叉概率,pm代表变异概率'''#遗传算法——单切点交叉#print("----------------------------------------------------------遗传算法(双切点交叉)----------------------------------------------------------")#产生初始种群X0=initialpopulation(NP,n,x0,x1)'''得到种群的最大适应值和对应的染色体'''value_max, valueX0_max = fitnessmax(X0, NP)print("--------------------遗传算法--------------------")print("初始最优解:\n{}".format(valueX0_max))print("初始最优函数值:\n{}".format(value_max))#存储最大适应值和对应的函数值的列表fitnessmax_list=[]X0max_list=[]#历史最大适应值history_max=0history=[]history_X0=[]for i in range(NG):'''得到种群的最大适应值和对应的染色体'''value_max,valueX0_max=fitnessmax(X0,NP)fitnessmax_list.append(value_max)X0max_list.append(valueX0_max)if i==0:history_max=value_maxhistory.append(history_max)history_X0.append(valueX0_max)else:if value_max>=history_max:history_max=value_maxhistory.append(history_max)history_X0.append(valueX0_max)else:history.append(history_max)history_X0.append(history_X0[i-1])#print("第{}代:{} value_max={}".format(i + 1, history_X0[i], history[i]))'''选择'''X1=selection(NP,X0)'''双切点交叉运算'''X2=crossover1(X1,pc,NP,4)'''变异运算'''X3=mutation(X2,pm,NP,4,-10,10)X0=X3print("最优解Best={}".format(history[-1]))#print("---------------------------------------------------------------进程结束---------------------------------------------------------------")'''返回历代的最优函数值和最优解'''return history,history_X02.3 GWO_vs_GA.py
import GWO1
import GA1
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=Falseif __name__=="__main__":'''得到遗传算法求解结果'''#最大迭代步数NG=1000#种群规模NP=100#交叉率pc=0.9#变异率pm=0.1#染色体基因数n=4#未知数的下限x0=-10#未知数的上限x1=10#进行双切点交叉的遗传运算historymax,historymaxX0=GA1.GA1(NP,NG,n,x0,x1,pc,pm)print("最优解:\n{}".format(historymaxX0[-1]))print("最优函数值:\n{}".format(historymax[-1]))'''得到灰狼优化算法的求解结果'''#最大迭代步数NG=1000#种群规模NP=100#数据维度dim=4#x允许的最大值和最小值x_max=10x_min=-10#系数向量初始值amax=2'''灰狼优化算法'''X_best,value_best=GWO1.GWO(NP,dim,NG-1,amax,x_max,x_min)print("最优解:\n{}".format(X_best[-1]))print("最优函数值:\n{}".format(value_best[-1]))'''绘制遗传算法和灰狼优化算法的优化过程'''plt.plot([int(i) for i in range(NG)],historymax,label="GA")plt.plot([int(i) for i in range(NG)],value_best,label="GWO",c="red")plt.title("遗传算法(GA)和灰狼优化算法(GWO)的优化过程")plt.xlabel("代数")plt.ylabel("函数值")plt.grid()plt.legend()plt.show()
2.4 运行结果

 三、基于莱维飞行改进的灰狼优化算法的python实现
三、基于莱维飞行改进的灰狼优化算法的python实现
import numpy as np
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False'''定义函数并求解函数值'''
def function(X0):''':param X0:解向量:return: 函数值'''s1=0for i in range(len(X0)):s1=s1+(X0[i])**2s2=0for i in range(len(X0)):s2=s2+np.cos(2*(np.pi)*X0[i])s=-20*np.exp(-0.2*(np.sqrt((1/len(X0))*s1)))-np.exp((1/len(X0))*s2)+20+np.ereturn s'''嵌入莱维飞行的灰狼优化算法'''
def LGWO(NP,dim,NG,amax,x_max,x_min):''':param NP:种群规模:param dim: 数据维度:param NG: 最大迭代步数:param amax: 系数向量初始值:param x_max: 解允许的最大值:param x_min: 解允许的最小值:return: 最优解和最优解的目标函数值''''''随机产生初始解'''X0=np.zeros((NP,dim))value0=[] #函数值for i in range(NP):X0[i]=np.random.uniform(low=x_min,high=x_max,size=(1, dim))value0.append(function(X0[i]))'''存储历史最优解和历史最优函数值'''X_best=[] #历史最优解value_best=[] #历史最优函数值'''对初始解的目标函数值进行升序排序,并一一对应得到相应的解'''#得到对目标函数值列表value0升序排列后的索引index_sort=np.argsort(np.array(value0))#对value0进行升序排列value0_sort=[value0[i] for i in index_sort]#对X0进行相应的排列X0_sort=[X0[i] for i in index_sort]'''得到初始解的最优解和最优函数值'''X_best.append(X0_sort[0])value_best.append(value0_sort[0])print("初始最优解:\n{}".format(X_best[0].tolist()))print("初始最优函数值:\n{}".format(value_best[0]))'''选出最优的两个个体,并获得它们的位置信息'''Xalpha=X0_sort[0]Xalpha_score=value0_sort[0]Xbeta=X0_sort[1]Xbeta_score=value0_sort[1]'''进行嵌入莱维飞行的灰狼优化算法'''for i in range(NG):'''计算系数向量的参数a'''ratio=i/NGa=amax*(1-ratio)for j in range(NP):'''边界处理'''for k in range(dim):if X0[j][k]>x_max:X0[j][k]=x_maxif X0[j][k]<x_min:X0[j][k]=x_min'''计算函数值'''value=function(X0[j])'''更新Alpha,Beta'''if value<Xalpha_score:Xalpha_score=valueXalpha=X0[j]elif value<Xbeta_score:Xbeta_score=valueXbeta=X0[j]'''更新所有个体'''Xbest=X0[0]valuebest=function(X0[0])for j in range(NP):for k in range(dim):r1=np.random.rand()r2=np.random.rand()A1=2*a*r1-aC1=2*r2D_alpha=np.abs(C1*Xalpha[k]-X0[j][k])r1=np.random.rand()r2=np.random.rand()A2=2*a*r1-aC2=2*r2D_beta=np.abs(C2*Xbeta[k]-X0[j][k])X0_old=X0[j]A=np.random.rand()if np.abs(A)<0.5:X0[j][k]=0.5*(Xalpha[k]-A1*D_alpha+Xbeta[k]-A2*D_beta)else:beta=1.5 #beta一般取1.5sigma_u=((math.gamma(1+beta)*math.sin(np.pi*beta/2))/(math.gamma((1+beta)/2)*beta*2**(0.5*(beta-1))))**(1/beta)u=np.random.normal(0,sigma_u)v=np.random.normal(0,1)alpha_levi=(0.01*u*(X0[j][k]-Xalpha[k]))/(np.abs(v)**(-beta))X0[j][k]=0.5*(Xalpha[k]-A1*D_alpha+Xbeta[k]-A2*D_alpha)+alpha_levi'''贪婪选择算法'''rnew=np.random.rand()p=np.random.rand()if function(X0[j])>function(X0_old) and rnew<p:X0[j]=X0_old'''计算函数值'''value1=function(X0[j])'''更新历史最优解和历史最优函数值'''if value1<valuebest:valuebest=value1Xbest=X0[j]if valuebest<value_best[-1]:value_best.append(valuebest)X_best.append(Xbest)else:value_best.append(value_best[-1])X_best.append(X_best[-1])'''绘制优化过程'''plt.plot([int(i) for i in range(NG+1)],value_best)plt.title("嵌入莱维飞行的灰狼优化算法(LGWO)的优化过程")plt.xlabel("代数")plt.ylabel("函数值")plt.grid()plt.show()return X_best[-1],value_best[-1]'''主函数'''
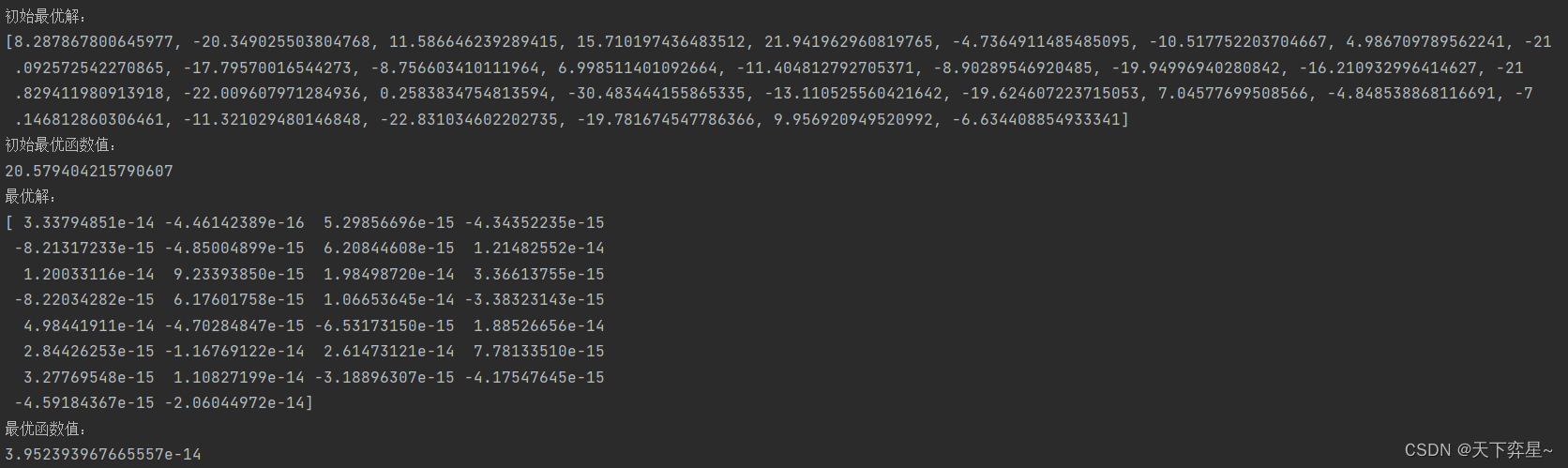
if __name__=="__main__":'''最大迭代步数'''NG=500'''种群规模'''NP=30'''数据维度'''dim=30'''x允许的最大值和最小值'''x_max=32x_min=-32'''系数向量初始值'''amax=2'''嵌入莱维飞行的灰狼优化算法'''X_best,value_best=LGWO(NP,dim,NG,amax,x_max,x_min)print("最优解:\n{}".format(X_best))print("最优函数值:\n{}".format(value_best)) 
相关文章:

灰狼优化算法(GWO)python
目录 一、灰狼优化算法的python实现 二、灰狼优化算法与遗传算法的对比分析(python) 2.1 GWO1.py 2.2 GA1.py 2.3 GWO_vs_GA.py 2.4 运行结果 三、基于莱维飞行改进的灰狼优化算法的python实现 一、灰狼优化算法的python实现 import numpy as …...
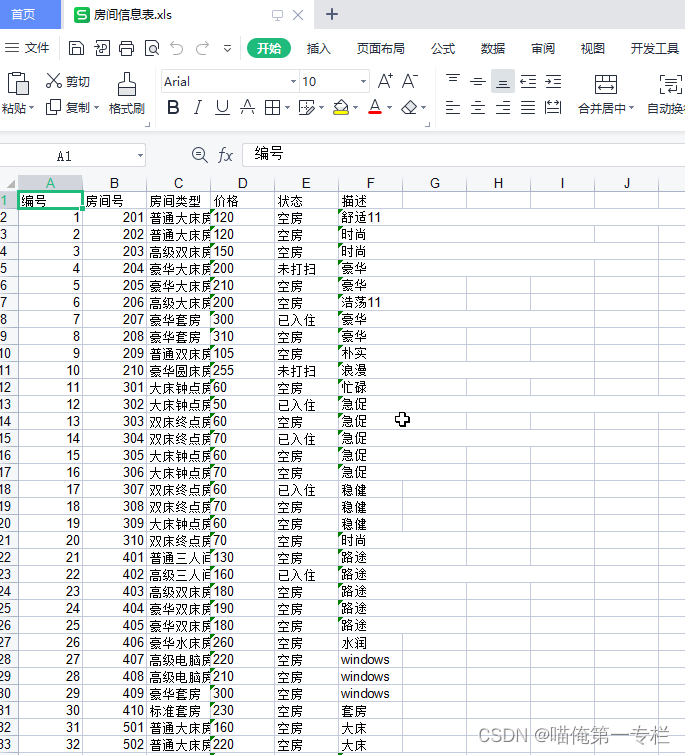
项目知识点总结-住房图片信息添加-Excel导出
(1)住房信息添加 Controller: RequestMapping("/add")public String add(Home home, Model model) throws IOException{String sqlPath null;//定义文件保存的本地路径String localPath"D:\\AnZhuang\\Java项目\\选题\\Xin-…...

第三届iEnglish全国ETP大赛决赛即将启动
如今,寓教于乐的学习方式越来越受到家长和孩子的欢迎,“玩中学”成为一种既能培养兴趣又有助于孩子成长的学习趋势。 以“玩转英语,用iEnglish”为活动主题的第三届全国ETP大赛即将于本周五(11月3日)迎来总决赛的抽签仪式。据主办方iEnglish智能英语学习解决方案相关负责人称,…...
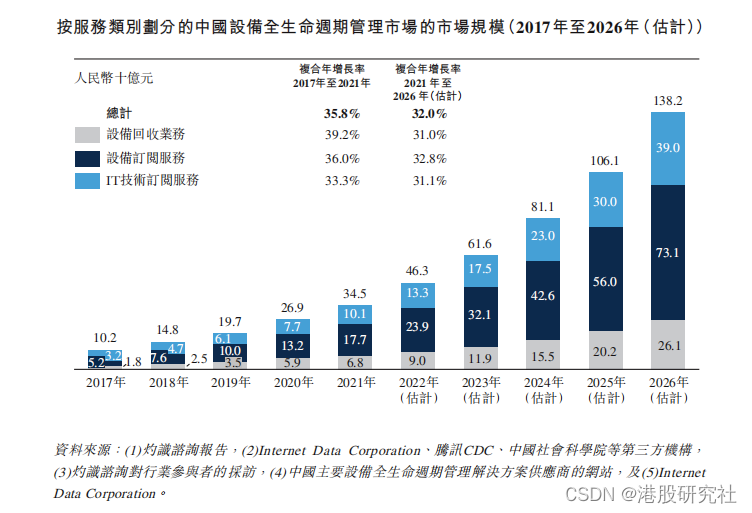
创造产业链协同优势后,凌雄科技在DaaS行业转动成长飞轮
企业服务领域,一直存在一种共识:做好很难,但一旦服务模式跑通了,得到了市场的认可,要滚起雪球就会事半功倍。 重资产、重运营的DaaS(设备及服务)赛道,是个非常典型的细分领域。在这…...

【protobuf】protobuf自定义数据格式,CMake编译C++文件读写自定义数据
protobuf自定义数据格式,CMake编译文件读写自定义数据 1.protobuf安装2.定义.proto文件3.编写main.cpp4.编写CMAkeLists配置文件5.运行 1.protobuf安装 protobuf库链接 2.定义.proto文件 新建一个Person.proto文件和一个Animal.proto文件,内容如下&…...

解决:http://localhost:8080 不在以下 request 合法域名列表中
在搭建资源服务器时,遇到了微信开发者工具中无法访问本地资源服务器的情况,报错如下: 参考一篇博文的方法,完美解决 【解决】http://localhost:8080 不在以下 request 合法域名列表中_localhost不在以下 request 合法域名列表中-…...

Linux普通用户提权(sudo)
文章目录 Linux普通用户提权(sudo)1、在sudoers文件添加普通用户2、测试 Linux普通用户提权(sudo) 1、在sudoers文件添加普通用户 正常来说,普通用户初始是不具备提权的能力的,比如执行sudo ls会出现报警告…...
链表指定节点的插入
向现有链表中插入结点,根据插入位置的不同,可分为以下 3 种情况: 插入到链表的头部,作为新的链表中第一个存有数据的结点(又称为”首元结点”);插入到链表中某两个结点之间的位置;插…...

解决问题Conda:CondaValueError: Malformed version string ‘~’ : invalid character(s)
解决问题Conda:CondaValueError: Malformed version string ‘~’ : invalid character(s) 背景 今天使用Conda构建项目运行环境的时候报错::CondaValueError: Malformed version string ‘~’ : invalid character(s) ##报错问题 在安装te…...
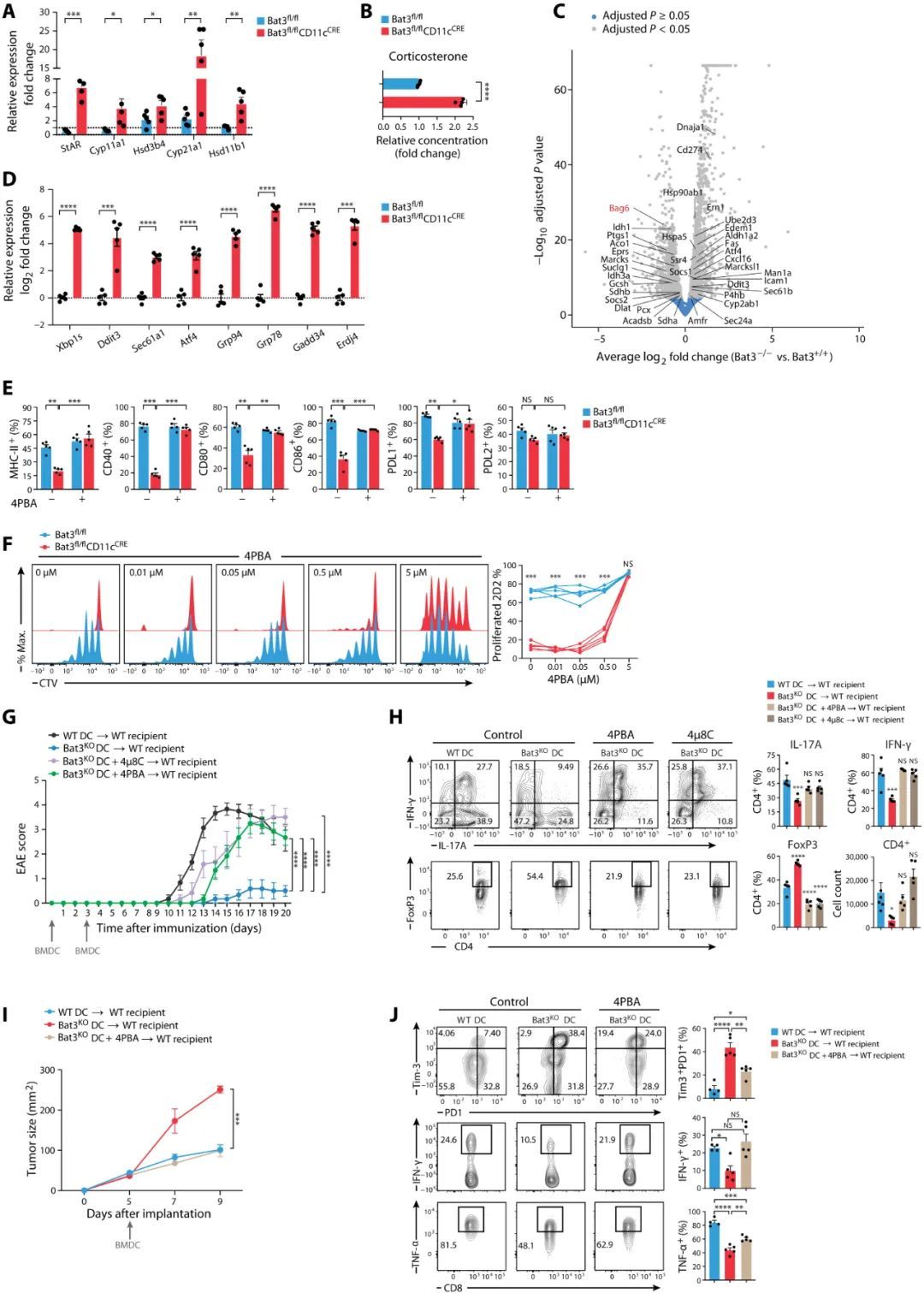
Sci Immunol丨Tim-3 适配器蛋白 Bat3 是耐受性树突状细胞
今天和大家分享一篇发表于2022年3月的文章,题目为“Tim-3 adapter protein Bat3 acts as an endogenous regulator of tolerogenic dendritic cell function”,发表在《Sci Immunol》杂志上。文章主要研究了Tim-3和其适配蛋白Bat3在调节免疫应答中的作用…...
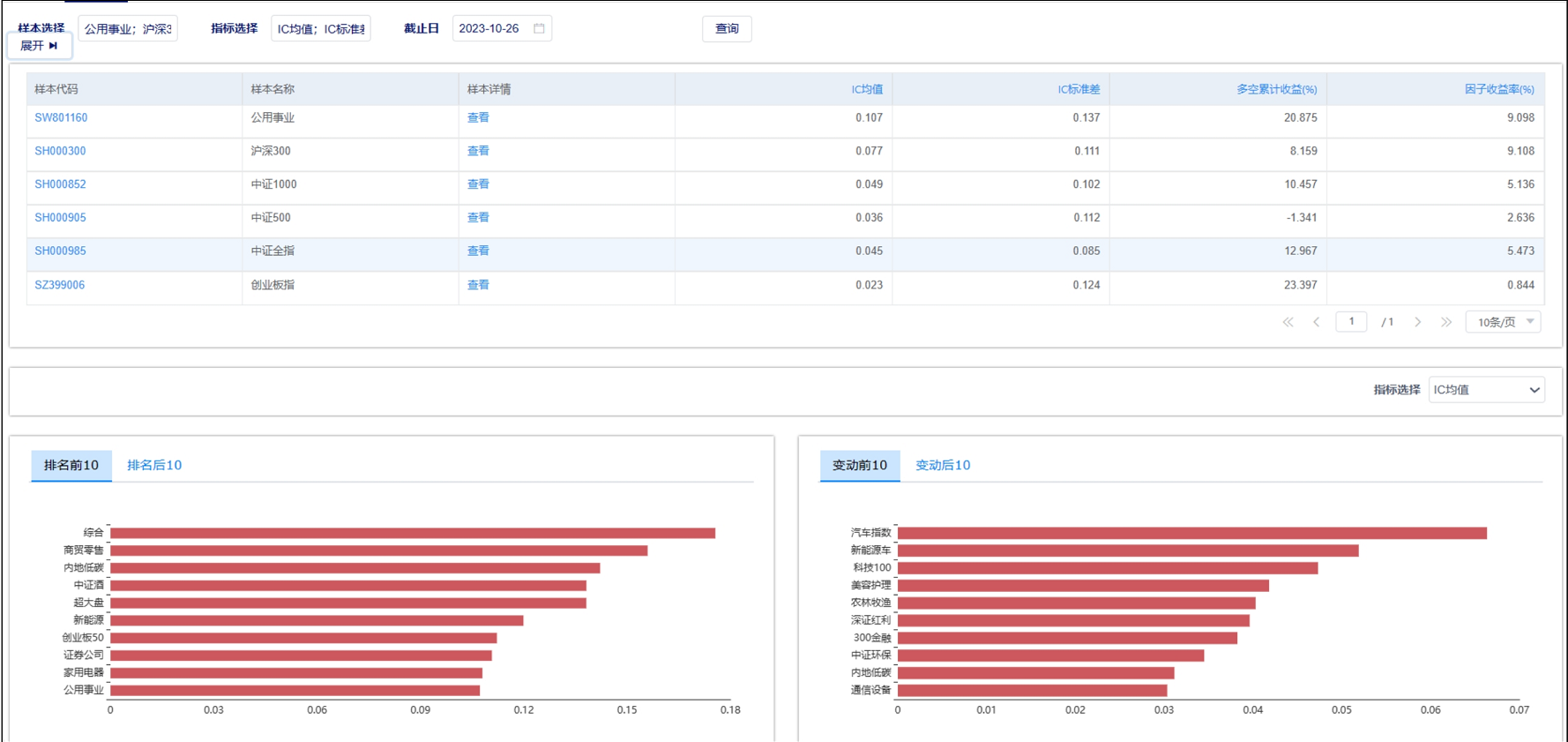
天软特色因子看板(2023.10 第14期)
该因子看板跟踪天软特色因子A05005(近一月单笔流通金额占比(%),该因子为近一个月单笔流通金额占比因子,用以刻画股票在收盘时,主力资金在总交易金额中所占的比重。 今日为该因子跟踪第14期,跟踪其在SW801160 (申万公用事业) 中的表…...
Photoshop(PS)2021版 安装教程(图文教程超详细)
软件:PS版本:2021语言:简体中文大小:2.26G安装环境:Win11/Win10(1809以上版本)硬件要求:CPU2.0GHz 内存4G(或更高,不支持7代以下CPU)下载通道①百度网盘丨64位…...

详解React:Props构建可复用UI的基石
React是一种流行的JavaScript库,用于构建用户界面。它的组件化架构使得开发人员能够轻松地构建可复用的UI元素,从而提高开发效率。在本文中,我们将探讨React中的组件和Props的重要性,以及如何利用它们来构建可复用的UI。 引言 在…...
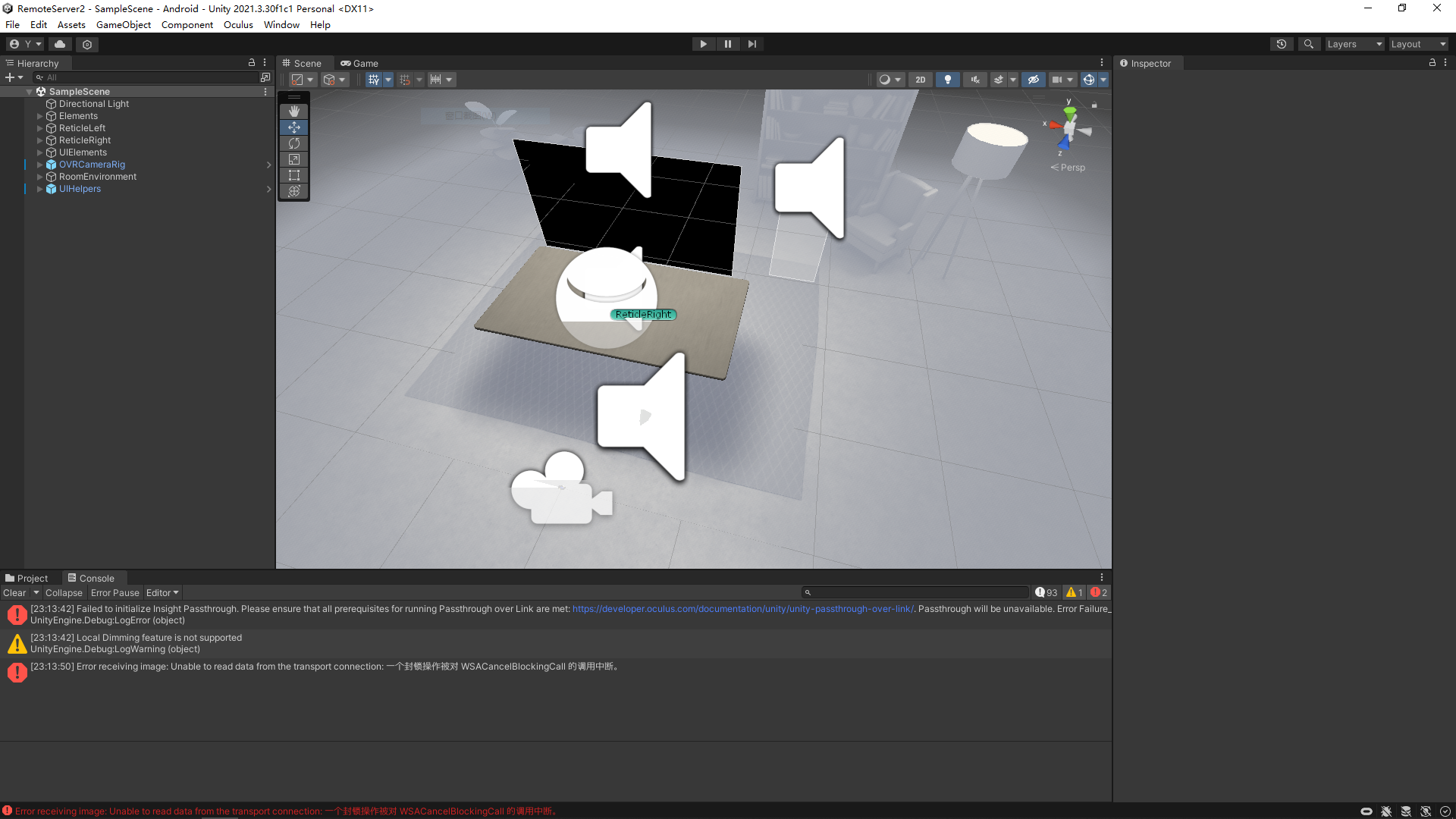
【Unity】【VR开发疑难】Unity运行就报无法启动XR Plugin
【现象】 连接Link后运行Unity的VR项目Link也无反映,Unity控制台报:无法启动XR Plugin,并说是由于Oculus头盔未连接导致。 【分析】 打开Oculus PC客户端,发现状态是连接正常。重启机器后,提示Oculus没有出于RunTim…...
)
本地启动Elasticsearch(docker启动)
一、es版本7.17.0 docker run -p 9200:9200 -p 9300:9300 -e "discovery.typesingle-node" -e ES_JAVA_OPTS"-Xms256m -Xmx256m" -d --name ES01 elasticsearch:7.17.0进入容器,修改/usr/share/elasticsearch/config/elasticsearch.yml 添加如…...
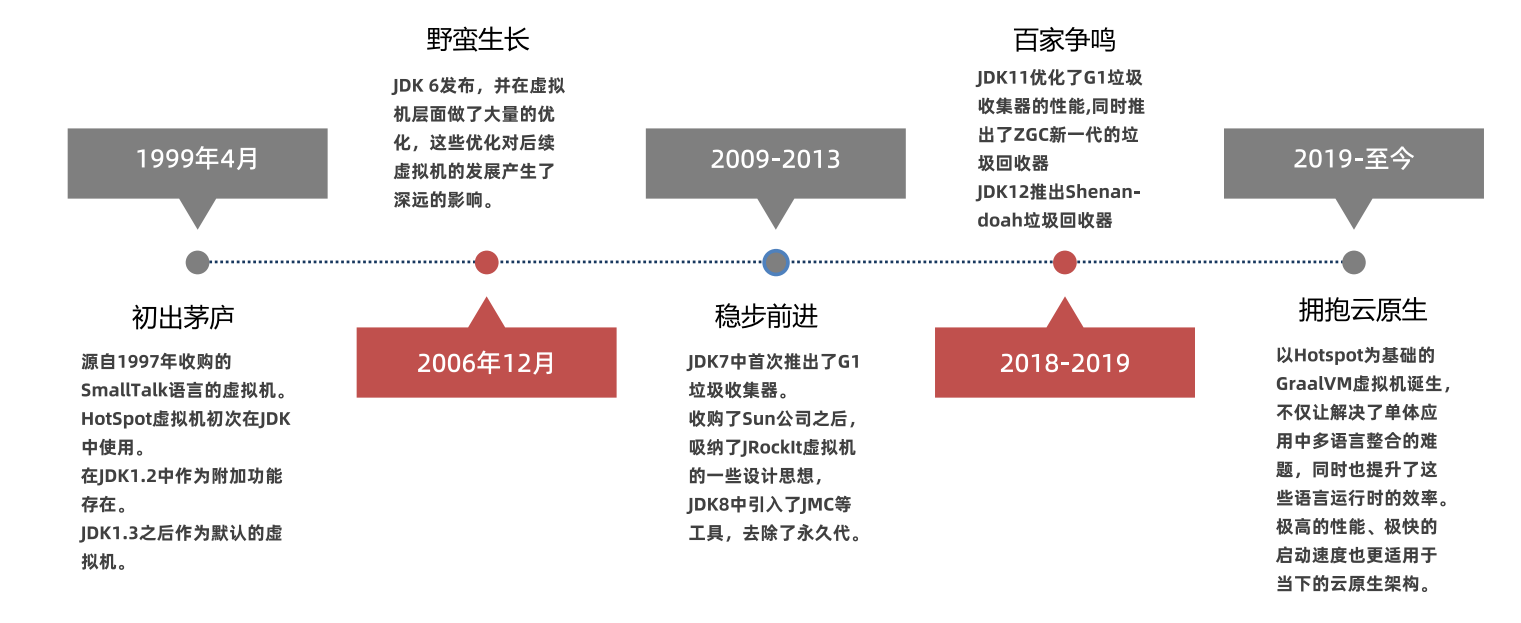
JVM修炼印记之初识
文章目录 JVM认识JVM的功能常见JVMHotSpot的发展历程 JVM认识 Java虚拟机(Java Virtual Machine,JVM)是一个用于执行Java字节码的虚拟计算机。它是Java语言的核心,可以在不同的操作系统和硬件平台上运行Java程序。 JVM负责将Java…...
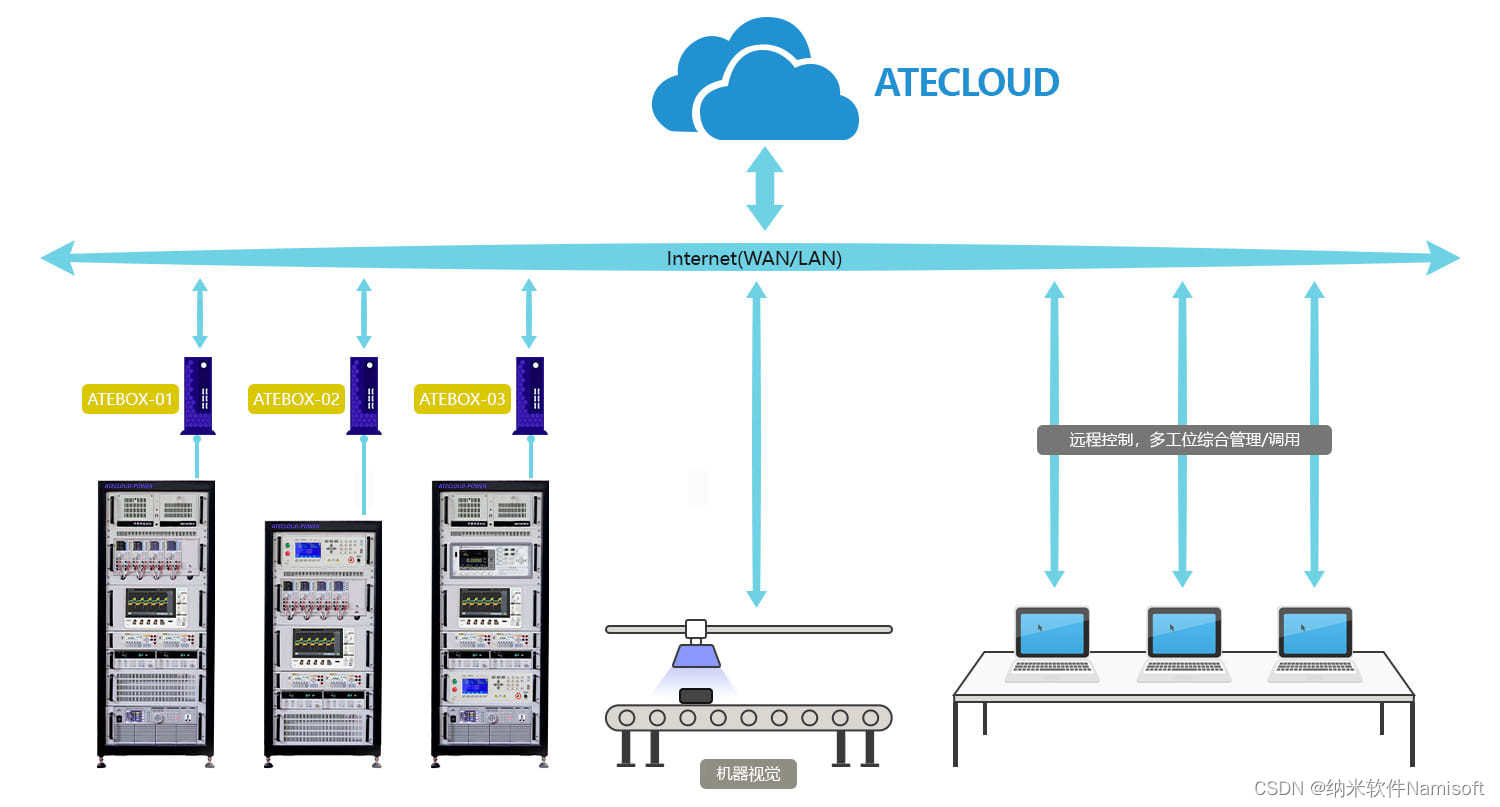
开关电源老化试验和性能检测系统软件
开关电源自动测试系统由PC(工控机)、测试工装、可编程直流电源、数字示波器、可编程直流电子负载、继电器模块等部分组成,并通过RS232/LAN通讯总线、测试夹具以及其它线缆等进行连接,为系统组成结构。PC与可编程直流电源、数字示波器、可编程直流电子负载…...
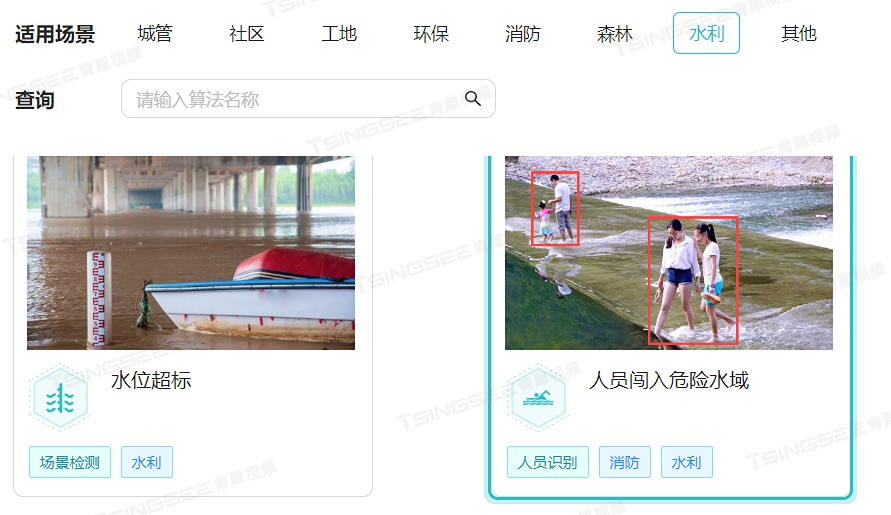
水库大坝可视化智能远程监管方案,助力安全监测智能巡检
一、背景需求 水库大坝作为防洪度汛的重要设施,其安全问题直接关系到人民群众的生命财产安全。因此,必须加强对大坝水库的安全管理,对水库除险加固和运行管护要消除存量隐患,实现常态化管理,同时要配套完善重点小型水…...

C#学习系列之虚方法和多态
C#学习系列之虚方法和多态 啰嗦设计原则(六大类其中之一)基类的引用使用 共性与差异虚方法和多态的武器使用 其他总结 啰嗦 基础学习。 设计原则(六大类其中之一) **依赖倒置原则:**依赖抽象类,不依赖具体…...
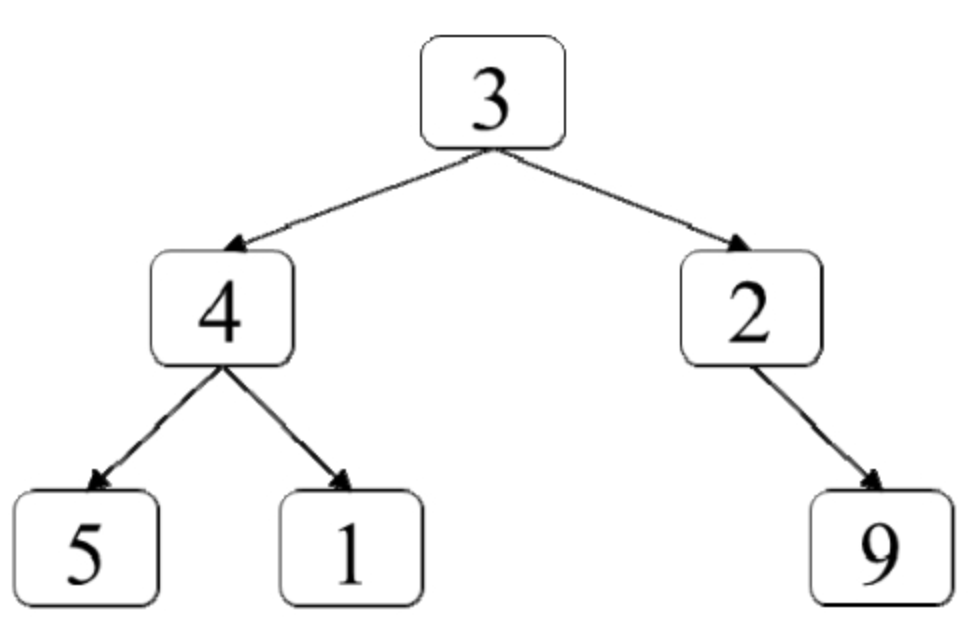
面试算法44:二叉树中每层的最大值
题目 输入一棵二叉树,请找出二叉树中每层的最大值。例如,输入图7.4中的二叉树,返回各层节点的最大值[3,4,9]。 分析:用一个队列实现二叉树的广度优先搜索 由于要找出二叉树中每层的最大值,因…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
