【机器学习】五、贝叶斯分类
我想说:“任何事件都是条件概率。”为什么呢?因为我认为,任何事件的发生都不是完全偶然的,它都会以其他事件的发生为基础。换句话说,条件概率就是在其他事件发生的基础上,某事件发生的概率。
条件概率是朴素贝叶斯模型的基础。
假设,你的xx公司正在面临着用户流失的压力。虽然,你能计算用户整体流失的概率(流失用户数/用户总数)。但这个数字并没有多大意义,因为资源是有限的,利用这个数字你只能撒胡椒面似的把钱撒在所有用户上,显然不经济。你非常想根据用户的某种行为,精确地估计一个用户流失的概率,若这个概率超过某个阀值,再触发用户挽留机制。这样能把钱花到最需要花的地方。
你搜遍脑子里的数据分析方法,终于,一个250年前的人名在脑中闪现。就是“贝叶斯Bayes”。你取得了近一个月的流失用户数、流失用户中未读消息大于5条的人数、近一个月的活跃用户数及活跃用户中未读消息大于5条的人数。在此基础上,你获得了一个“一旦用户未读消息大于5条,他流失的概率高达%”的精确结论。怎么实现这个计算呢?先别着急,为了解释清楚贝叶斯模型,我们先定义一些名词。
-
概率(Probability)——0和1之间的一个数字,表示一个特定结果发生的可能性。比如投资硬币,“正面朝上”这个特定结果发生的可能性为0.5,这个0.5就是概率。换一种说法,计算样本数据中出现该结果次数的百分比。即你投一百次硬币,正面朝上的次数基本上是50次。
-
几率(Odds)——某一特定结果发生与不发生的概率比。如果你明天电梯上遇上你暗恋的女孩的概率是0.1,那么遇不上她的概率就是0.9,那么遇上暗恋女孩的几率就是1/9,几率的取值范围是0到无穷大。
-
似然(Likelihood)——两个相关的条件概率之比,即给定B发生的情况下,某一特定结果A发生的概率和给定B不发生的情况下A发生的概率之比。另一种表达方式是,给定B的情况下A发生的几率和A的整体几率之比。两个计算方式是等价的。
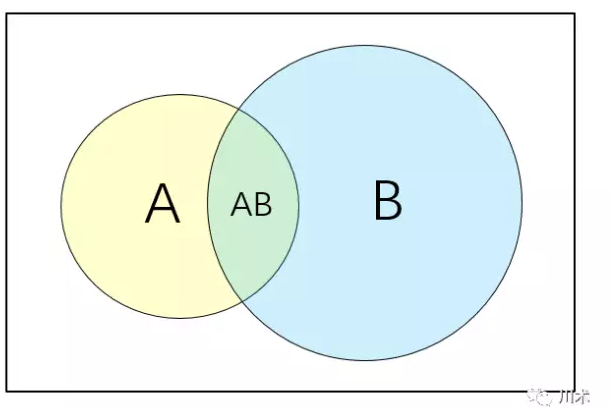
因为上面在似然当中提到了条件概率,那么我们有必要将什么是条件概率做更详尽的阐述。
如上面的韦恩图,我们用矩形表示一个样本空间,代表随机事件发生的一切可能结果。的在统计学中,我们用符号P表示概率,A事件发生的概率表示为P(A)。两个事件间的概率表达实际上相当繁琐,我们只介绍本书中用得着的关系:
-
A事件与B事件同时发生的概率表示为P(A∩B),或简写为P(AB)即两个圆圈重叠的部分。
-
A不发生的概率为1-P(A),写为P(~A),即矩形中除了圆圈A以外的其他部分。
-
A或者B至少有一个发生的概率表示为P(A∪B),即圆圈A与圆圈B共同覆盖的区域。
-
在B事件发生的基础上发生A的概率表示为P(A|B),这便是我们前文所提到的条件概率,图形上它有AB重合的面积比上B的面积。
回到我们的例子。以P(A)代表用户流失的概率,P(B)代表用户有5条以上未读信息的概率,P(B|A)代表用户流失的前提下未读信息大于5条的概率。我们要求未读信息大于5条的用户流失的概率,即P(A|B),贝叶斯公式告诉我们:
P(A|B)=P(AB)/P(B)
=P(B|A)*P(A)/P(B)
从公式中可知,如果要计算B条件下A发生的概率,只需要计算出后面等式的三个部分,B事件的概率(P(B)),是B的先验概率、A属于某类的概率(P(A)),是A的先验概率、以及已知A的某个分类下,事件B的概率(P(B|A)),是后验概率。
如果要确定某个样本归属于哪一类,则需要计算出归属不同类的概率,再从中挑选出最大的概率
我们把上面的贝叶斯公式写出这样,也许你能更好的理解:
MAX(P(Ai|B))=MAX(P(B|Ai)*P(Ai)/P(B))
而这个公式告诉我们,需要计算最大的后验概率,只需要计算出分子的最大值即可,而不同水平的概率P(C)非常容易获得,故难点就在于P(X|C)的概率计算。而问题的解决,正是聪明之处,即贝叶斯假设变量X间是条件独立的,故而P(X|C)的概率就可以计算为:
P(B|Ai) =P(B1/Ai)*P(B2/Ai)*P(B3/Ai)*.....*P(Bn/Ai)
如下图,由这个公式我们就能轻松计算出,在观察到某用户的未读信息大于5条时,他流失的概率为80%。80%的数值比原来的30%真是靠谱太多了。
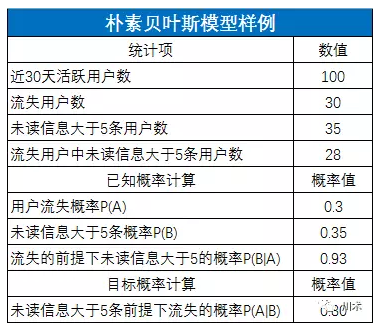
当然,现实情况并不会像这个例子这么理想化。大家会问,凭什么你就会想到用“未读消息大于5条”来作为条件概率?我只能说,现实情况中,你可能要找上一堆觉得能够凸显用户流失的行为,然后一一做贝叶斯规则,来测算他们是否能显著识别用户流失。寻找这个字段的效率,取决于你对业务的理解程度和直觉的敏锐性。另外,你还需要定义“流失”和“活跃”,还需要定义贝叶斯规则计算的基础样本,这决定了结果的精度。
-
利用全概率公式的一个例子
朴素贝叶斯的应用不止于此,我们再例举一个更复杂,但现实场景也更实际的案例。假设你为了肃清电商平台上的恶性商户(刷单、非法交易、恶性竞争等),委托算法团队开发了一个识别商家是否是恶性商户的模型M1。为什么要开发模型呢?因为之前识别恶性商家,你只能通过用户举报和人肉识别异常数据的方式,人力成本高且速率很慢。你指望有智能的算法来提高效率。
之前监察团队的成果告诉我们,目前平台上的恶性商户比率为0.2%,记为P(E),那么P(~E)就是99.8%。利用模型M1进行检测,你发现在监察团队已判定的恶性商户中,由模型M1所判定为阳性(恶性商户)的人数占比为90%,这是一个条件概率,表示为P(P|E)=90%;在监察团队判定为健康商户群体中,由模型M1判定为阳性的人数占比为8%,表示为P(P|~E)=8%。乍看之下,你是不是觉得这个模型的准确度不够呢?感觉对商户有8%的误杀,还有10%的漏判。其实不然,这个模型的结果不是你想当然的这么使用的
这里,我们需要使用一个称为“全概率公式”的计算模型,来计算出在M1判别某个商户为恶性商户时,这个结果的可信度有多高。这正是贝叶斯模型的核心。当M1判别某个商户为恶性商户时,这个商户的确是恶性商户的概率由P(E|P)表示:
P(E|P)
=P(P|E)*P(E) / (P(E)*P(P|E)+P(~E)*P(P|~E))
上面就是全概率公式。要知道判别为恶性商户的前提下,该商户实际为恶性商户的概率,需要由先前的恶性商户比率P(E),以判别的恶性商户中的结果为阳性的商户比率P(P|E),以判别为健康商户中的结果为阳性的比率P(P|~E),以判别商户中健康商户的比率P(~E)来共同决定。
P(E) 0.2%
P(P|E) 90%
P(~E) 99.8%
P(P|~E) 8%
P(E|P)= P(P|E)*P(E) / (P(E)*P(P|E)+P(~E)*P(P|~E)) 2.2%
由上面的数字,带入全概率公式后,我们获得的结果为2.2%。也就是说,根据M1的判别为阳性的结果,某个商户实际为恶性商户的概率为2.2%,是不进行判别的0.2%的11倍。
你可能认为2.2%的概率并不算高。但实际情况下你应该这么思考:被M1模型判别为恶性商户,说明这家商户做出恶性行为的概率是一般商户的11倍,那么,就非常有必要用进一步的手段进行检查了。
恶性商户判别模型真正的使用逻辑应该是如下图所示。我们先用M1进行一轮判别,结果是阳性的商户,说明出现恶性行为的概率是一般商户的11倍,那么有必要用精度更高的方式进行判别,或者人工介入进行检查。精度更高的检查和人工介入,成本都是非常高的。因此M1模型的使用能够使我们的成本得到大幅节约。
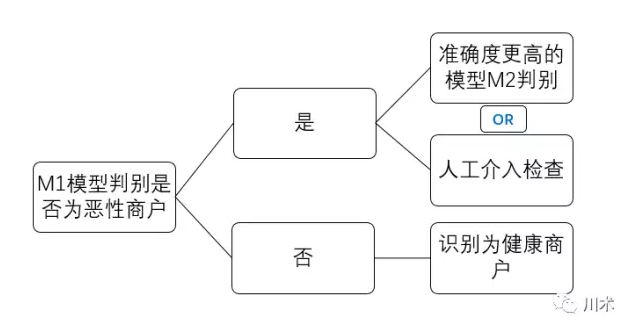
贝叶斯模型在很多方面都有应用,我们熟知的领域就有垃圾邮件识别、文本的模糊匹配、欺诈判别、商品推荐等等。通过贝叶斯模型的阐述,大家应该有这样的一种体会:分析模型并不取决于多么复杂的数学公式,多么高级的软件工具,多么高深的算法组合;它们的原理往往是通俗易懂的,实现起来也没有多高的门槛。比如贝叶斯模型,用Excel的单元格和加减乘除的符号就能实现。所以,不要觉得数据分析建模有多遥远,其实就在你手边。
附:
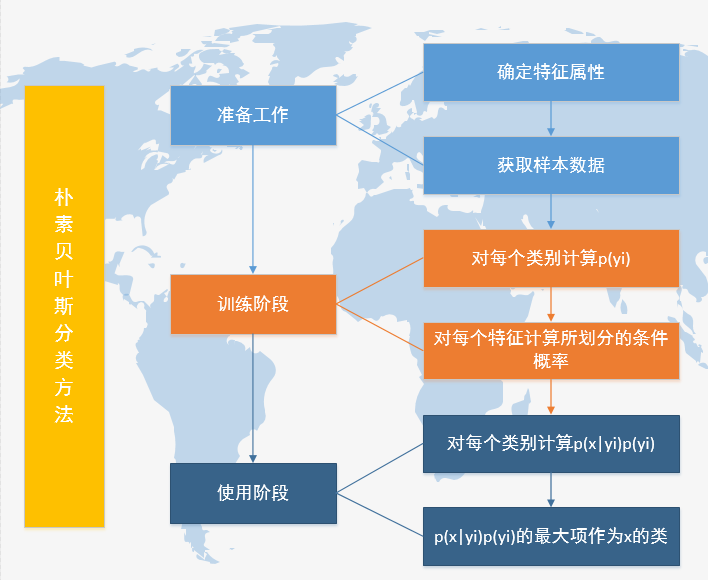
朴素贝叶斯分类适用解决的问题
在考虑一个结果的概率时候,要考虑众多的属性,贝叶斯算法利用所有可能的数据来进行修正预测,如果大量的特征产生的影响较小,放在一起,组合的影响较大,适合于朴素贝叶斯分类。
应用范围:
贝叶斯定理广泛应用于决策分析。先验概率经常是由决策者主观估计的。在选择最佳决策时,会在取得样本信息后计算后验概率以供决策者使用。
那在R语言中,是如何实现朴素贝叶斯算法的落地的?
R语言中的klaR包就提供了朴素贝叶斯算法实现的函数NaiveBayes,我们来看一下该函数的用法及参数含义:
NaiveBayes(formula, data, ..., subset, na.action= na.pass)
NaiveBayes(x, grouping, prior, usekernel= FALSE, fL = 0, ...)
formula指定参与模型计算的变量,以公式形式给出,类似于y=x1+x2+x3;
data用于指定需要分析的数据对象;
na.action指定缺失值的处理方法,默认情况下不将缺失值纳入模型计算,也不会发生报错信息,当设为“na.omit”时则会删除含有缺失值的样本;
x指定需要处理的数据,可以是数据框形式,也可以是矩阵形式;
grouping为每个观测样本指定所属类别;
prior可为各个类别指定先验概率,默认情况下用各个类别的样本比例作为先验概率;
usekernel指定密度估计的方法(在无法判断数据的分布时,采用密度密度估计方法),默认情况下使用正态分布密度估计,设为TRUE时,则使用核密度估计方法;
fL指定是否进行拉普拉斯修正,默认情况下不对数据进行修正,当数据量较小时,可以设置该参数为1,即进行拉普拉斯修正。
R语言实战
本次实战内容的数据来自于UCI机器学习网站,后文会给出数据集合源代码的链接。
# 下载并加载所需的应用包
if(!suppressWarnings(require(‘caret’))){
install.packages(‘caret’)
require(‘caret’)
}
if(!suppressWarnings(require(‘klaR’))){
install.packages(‘klaR’)
require(‘klaR’)
}
if(!suppressWarnings(require(‘pROC’))){
install.packages(‘pROC’)
require(‘pROC’)
}
# 读取蘑菇数据集
mydata <- read.csv(file = file.choose())
# 简单的了解一下数据
str(mydata)
summary(mydata)
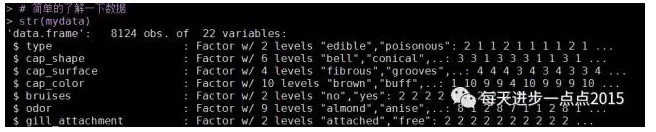
该数据集中包含了8124个样本和22个变量(如蘑菇的颜色、形状、光滑度等)。
# 抽样,并将总体分为训练集和测试集
set.seed(12)
index <- sample(1:nrow(mydata), size = 0.75*nrow(mydata))
train <- mydata[index,]
test <- mydata[-index,]
# 大致查看抽样与总体之间是否吻合
prop.table(table(mydata$type))
prop.table(table(train$type))
prop.table(table(test$type))
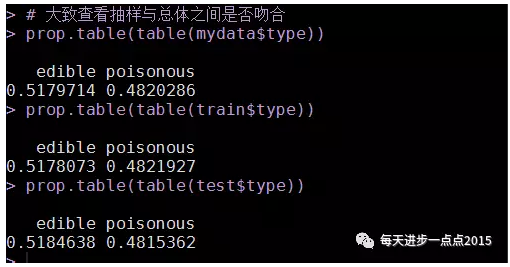
原始数据中毒蘑菇与非毒蘑菇之间的比较比较接近,通过抽选训练集和测试集,发现比重与总体比例大致一样,故可认为抽样的结果能够反映总体状况,可进一步进行建模和测试。
由于影响蘑菇是否有毒的变量有21个,可以先试着做一下特征选择,这里我们就采用随机森林方法(借助caret包实现特征选择的工作)进行重要变量的选择:
#构建rfe函数的控制参数(使用随机森林函数和10重交叉验证抽样方法,并抽取5组样本)
rfeControls_rf <- rfeControl(functions = rfFuncs,method = 'cv',repeats = 5)
#使用rfe函数进行特征选择
fs_nb <- rfe(x = train[,-1],y = train[,1],sizes = seq(4,21,2),rfeControl = rfeControls_rf)
fs_nb
plot(fs_nb, type = c('g','o'))
fs_nb$optVariables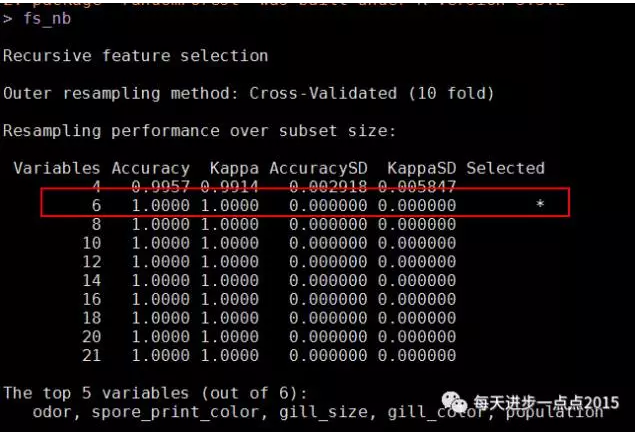
结果显示,21个变量中,只需要选择6个变量即可,下图也可以说明这一点:
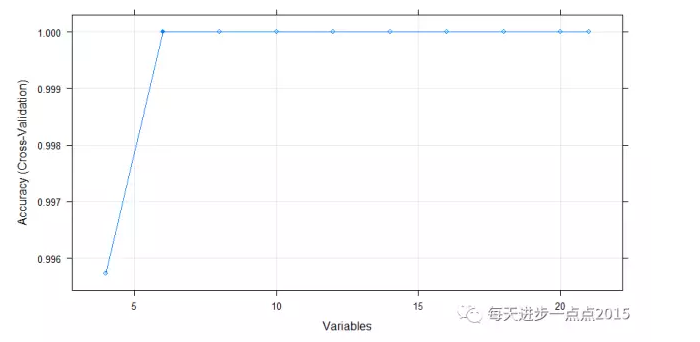
所需要选择的变量是:

接下来,我们就针对这6个变量,使用朴素贝叶斯算法进行建模和预测:
# 使用klaR包中的NaiveBayes函数构建朴素贝叶斯算法
vars <- c('type',fs_nb$optVariables)
fit <- NaiveBayes(type ~ ., data = train[,vars])
# 预测
pred <- predict(fit, newdata = test[,vars][,-1])
# 构建混淆矩阵
freq <- table(pred$class, test[,1])
freq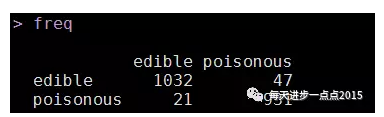
# 模型的准确率
accuracy <- sum(diag(freq))/sum(freq)
accuracy
# 模型的AUC值
modelroc <- roc(as.integer(test[,1]), as.integer(factor(pred$class)))
# 绘制ROC曲线
plot(modelroc, print.auc = TRUE, auc.polygon = TRUE, grid = c(0.1,0.2), grid.col = c('green','red'),max.auc.polygon = TRUE, auc.polygon.col = 'steelblue')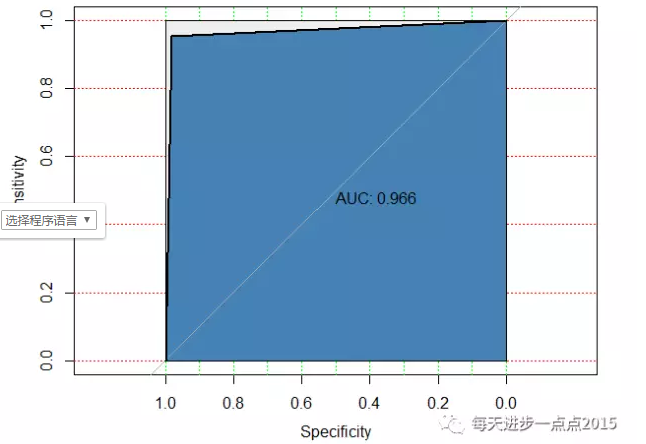
通过朴素贝叶斯模型,在测试集中,模型的准确率约为97%,而且AUC的值也非常高,一般超过0.8就说明模型比较理想了。
参考来源于:https://ask.hellobi.com/blog/chuanshu108/6036
https://ask.hellobi.com/blog/lsxxx2011/6381
相关文章:

【机器学习】五、贝叶斯分类
我想说:“任何事件都是条件概率。”为什么呢?因为我认为,任何事件的发生都不是完全偶然的,它都会以其他事件的发生为基础。换句话说,条件概率就是在其他事件发生的基础上,某事件发生的概率。 条件概率是朴…...

k8s 资源管理方式
k8s中资源管理方式可以划分为下面的几种:命令式对象管理、命令式对象配置、声明式对象配置。 命令式对象管理 命令式对象管理:直接使用命令的方式来操作k8s资源, 这种方式操作简单,但是无法审计和追踪。 kubectl run nginx-pod --imagengi…...

Golang Gin 接口返回 Excel 文件
文章目录 1.Web 页面导出数据到文件由后台实现还是前端实现?2.Golang Excel 库选型3.后台实现示例4.xlsx 库的问题5.小结参考文献 1.Web 页面导出数据到文件由后台实现还是前端实现? Web 页面导出表数据到 Excel(或其他格式)可以…...

实战之巧用header头
案例: 遇到过三次 一次是更改accept,获取到tomcat的绝对路径,结合其他漏洞获取到shell。 一次是更改accept,越权获取到管理员的MD5加密,最后接管超管权限。 一次是更改accept,结合参数获取到key。 这里以越…...

[AUTOSAR][诊断管理][ECU][$36] 数据传输
文章目录 一、简介二、服务请求报文定义三、服务请求报文中参数定义(1)blockSequenceCounter(2)transferRequestParameterRecord三、肯定响应(1)blockSequenceCounter(2)transferResponseParameterRecord四、支持的NRC五、示例代码36_transfer_data.c一、简介 这个服务…...
sw 怎么装新版本
我们在安装solidworks时,有时候会提示A newer version of this applic ation is already installed. Installation stopped.如下图所示 这时候需要点继续安装 然后会出现下图所示情况,vba7.1安装未成功 这是因为我们电脑中以前安装过更高版本的solidw…...
正点原子嵌入式linux驱动开发——Linux 音频驱动
音频是最常用到的功能,音频也是linux和安卓的重点应用场合。STM32MP1带有SAI接口,正点原子的STM32MP1开发板通过此接口外接了一个CS42L51音频DAC芯片,本章就来学习一下如何使能CS42L51驱动,并且CS42L51通过芯片来完成音乐播放与录…...

conda相关的命令操作
准备切换conda环境 cd C:\ProgramData\Anaconda3\Scripts查看所有环境 conda info --envs选择环境 activate pytorch安装torch pip install D:\installPackage\torch-1.2.0-cp36-cp36m-win_amd64.whl安装torchvision pip install D:\installPackage\torchvision-0.4.0-cp3…...

如何快速使用Vue3在electron项目开发chrome Devtools插件
1、建立Vue项目 为了方便快速建立项目,我已经写好脚手架,直接clone项目,快速开发 点击快速进入源代码 拉取代码 git clone https://github.com/xygengcn/electron-devtool.git安装依赖 yarn运行项目 yarn dev打包项目 yarn build2、安装…...
干洗店服务预约小程序有什么作用
要说干洗店,近些年的需求度非常高,一方面是人们生活品质提升,另一方面则是各种服饰对洗涤要求提升等,很多人的衣服很多也会通过干洗店进行清洁。 而对从业商家来说,市场庞大一方面需要不断进行市场教育、品牌提升&…...

【跟小嘉学 Rust 编程】三十四、Rust的Web开发框架之一: Actix-Web的进阶
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...
——Xshell安装)
软件安装(1)——Xshell安装
一、前言 本篇文章主要用于介绍Xshell破解版的安装 二、具体步骤 1. 下载Xshell7 链接:https://pan.baidu.com/s/1sFZz1uPb7yeDl6dlM4xtpg 提取码:a7m8 2. 安装Xshell7 选择文件安装目录后安装即可...
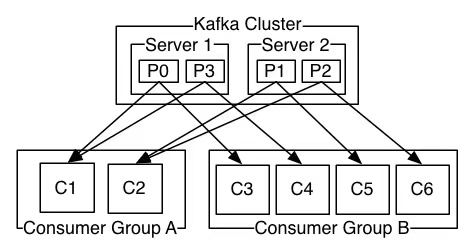
Kafka基本原理、生产问题总结及性能优化实践 | 京东云技术团队
Kafka是最初由Linkedin公司开发,是一个分布式、支持分区的(partition)、多副本的(replica),基于zookeeper协调的分布式消息系统,它的最大的特性就是可以实时的处理大量数据以满足各种需求场景&a…...
)
java8利用Stream方法求两个List对象的交集、差集与并集(即:anyMatch和allMatch和noneMatch的区别详解)
1、anyMatch 判断数据列表中是否存在任意一个元素符合设置的predicate条件,如果是就返回true,否则返回false。 接口定义: boolean anyMatch(Predicate<? super T> predicate); 方法描述: 在anyMatch 接口定义中是接收 P…...

Centos7下生成https自签名证书
1、安装openssl yum install openssl2、生成带密码的私有秘钥文件 openssl genrsa -des3 -out server.key 2048使用带密码的私有秘钥文件时需要输入密码,这里直接输入:123456 3、生成不带密码的私有秘钥文件 openssl rsa -in server.key -out serve…...

从中序和后序遍历序列构造二叉树
注意:该解法是基于二叉树中的值不存在重复所写的。 代码如下,可开袋即食 class Solution {private Map<Integer,Integer> map;public TreeNode buildTree(int[] inorder, int[] postorder) {map new HashMap<>();for(int i 0; i < in…...
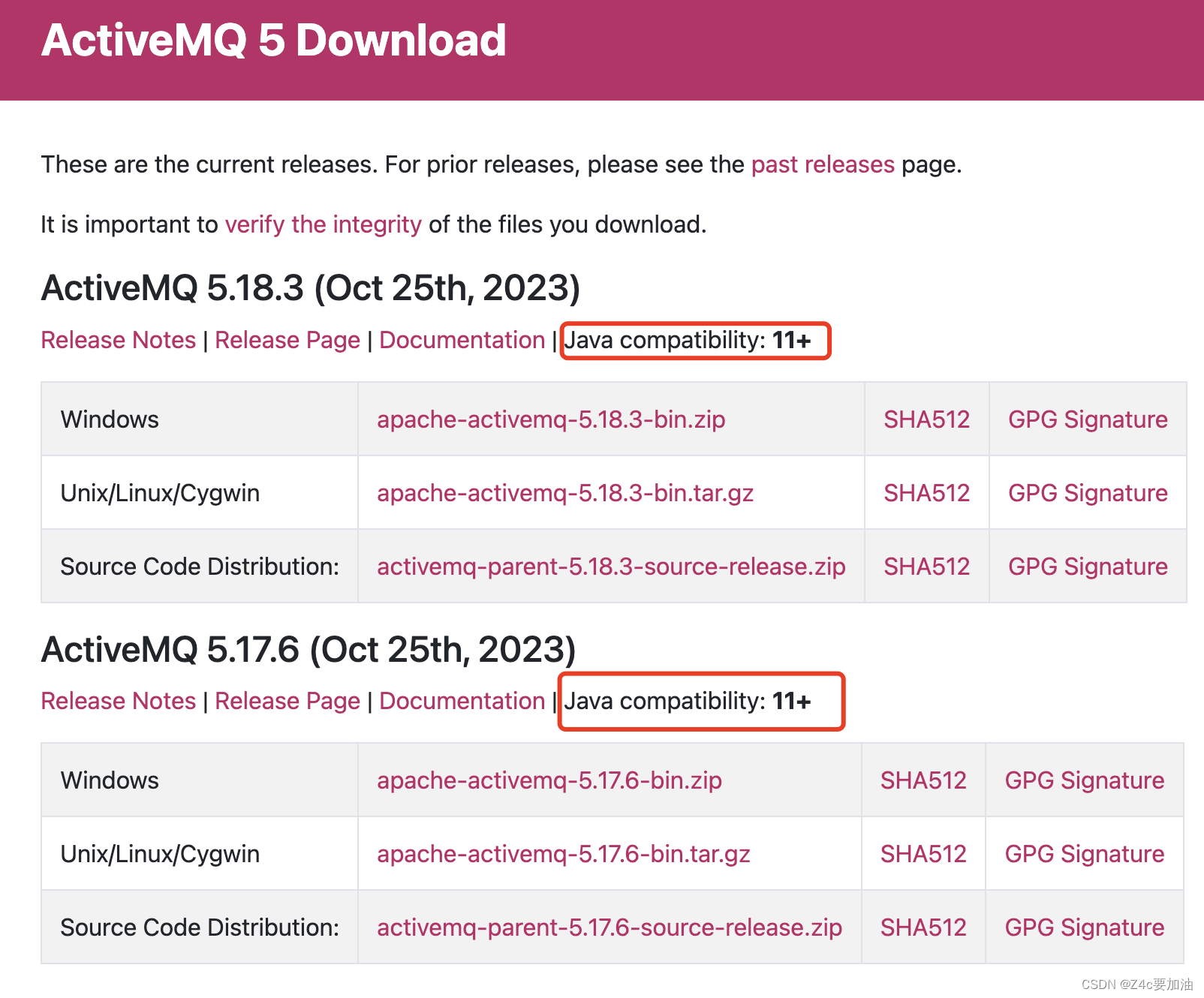
Apache ActiveMQ (版本 < 5.18.3) (CNVD-2023-69477)RCE修复方案/缓解方案
一、漏洞描述 Apache ActiveMQ 是美国阿帕奇(Apache)基金会的一套开源的消息中间件,它支持 Java 消息服务、集群、Spring Framework 等。 二、漏洞成因 ActiveMQ 默认开放了 61616 端口用于接收 OpenWire 协议消息,由于针对异常…...
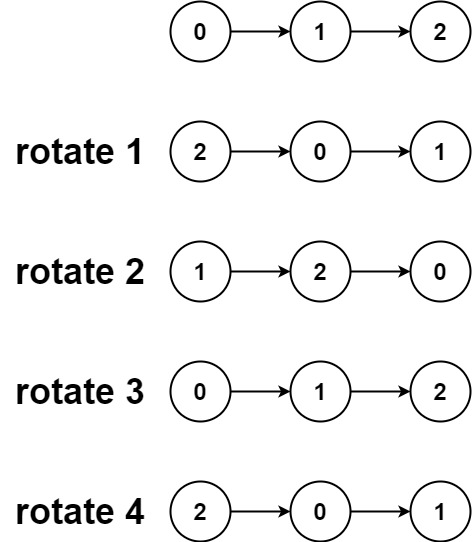
61. 旋转链表、Leetcode的Python实现
博客主页:🏆李歘歘的博客 🏆 🌺每天不定期分享一些包括但不限于计算机基础、算法、后端开发相关的知识点,以及职场小菜鸡的生活。🌺 💗点关注不迷路,总有一些📖知识点&am…...
基于tpshop开发多商户源码支持手机端+商家+门店 +分销+淘宝数据导入+APP+可视化编辑
tpshop多商户源码,tpshop商城源码,tpshop b2b2c源码-支持手机端商家门店 分销淘宝数据导入APP可视化编辑 tpshop商城源码算是 thinkphp框架里做的比较早 比较好的源码了,写法简明 友好面向程序猿。 这是一款前几年的版本 虽然后台看着好了些,丝毫不影响…...
ElasticSearch深度解析入门篇:高效搜索解决方案的介绍与实战案例讲解,带你避坑
ElasticSearch深度解析入门篇:高效搜索解决方案的介绍与实战案例讲解,带你避坑 1.Elasticsearch 产生背景 大规模数据如何检索 如:当系统数据量上了 10 亿、100 亿条的时候,我们在做系统架构的时候通常会从以下角度去考虑问题&a…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
