从中序和后序遍历序列构造二叉树
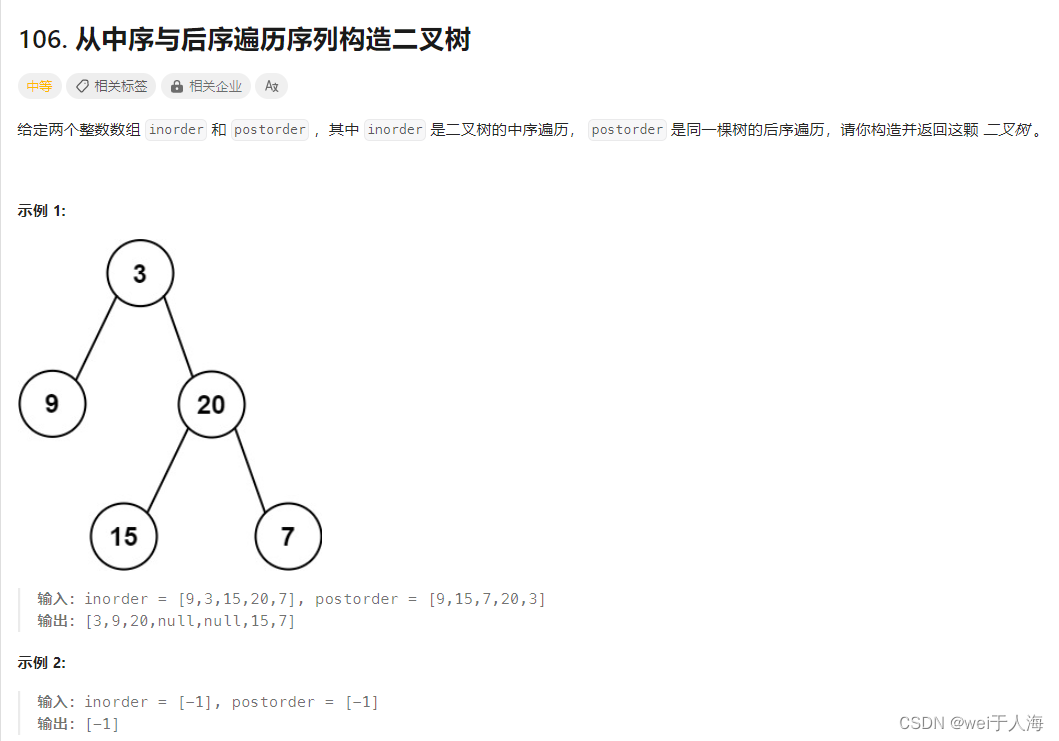

注意:该解法是基于二叉树中的值不存在重复所写的。
代码如下,可开袋即食
class Solution {private Map<Integer,Integer> map;public TreeNode buildTree(int[] inorder, int[] postorder) {map = new HashMap<>();for(int i = 0; i < inorder.length; i++){map.put(inorder[i], i);//记录中序遍历的根节点位置}return build(inorder, postorder, 0, inorder.length-1, 0, inorder.length- 1);}public TreeNode build(int[] inorder, int[] postorder, int i_left, int i_right, int p_left, int p_right){if(p_left > p_right) return null;int r_root = map.get(postorder[p_right]);//中序遍历根节点位置TreeNode root = new TreeNode(postorder[p_right]);//创建根节点root.left = build(inorder, postorder, i_left, r_root-1, p_left, p_left +r_root-i_left-1);root.right = build(inorder, postorder, r_root+1, i_right, p_left + r_root-i_left, p_right-1);return root;}
}
这里主要的问题就是递归的边界问题了。
i_left:中序遍历的左边界
i_right:中序遍历的右边界
p_left:后序遍历的左边界
p_rigjt:后序遍历的右边界
递归的时候,需要注意里面的边界问题。
在左子树递归的时候,难的是后序遍历的边界处理。
i_left不变,i_right自然就变成r_root-1了
p_left不变,而p_right即左子树的长度了,即p_left+root-1-i_left。
为什么是这样算的?因为后序遍历的结果,前面一部分是左子树,后面一部分是柚子树,最后是根节点,如果不懂的话,可以自己画图,然后把中序和后序写出来,自己去想我这句话说的是什么意思。
然后右子树递归的时候,同样,难的是后序遍历的边界处理。
i_left变成r_root+1,i_right不变
p_left变成p_left+r_root-i_left,r_right向左移动一位,p_right-1
后序遍历的左右边界是这一题的难点。
相关文章:

从中序和后序遍历序列构造二叉树
注意:该解法是基于二叉树中的值不存在重复所写的。 代码如下,可开袋即食 class Solution {private Map<Integer,Integer> map;public TreeNode buildTree(int[] inorder, int[] postorder) {map new HashMap<>();for(int i 0; i < in…...
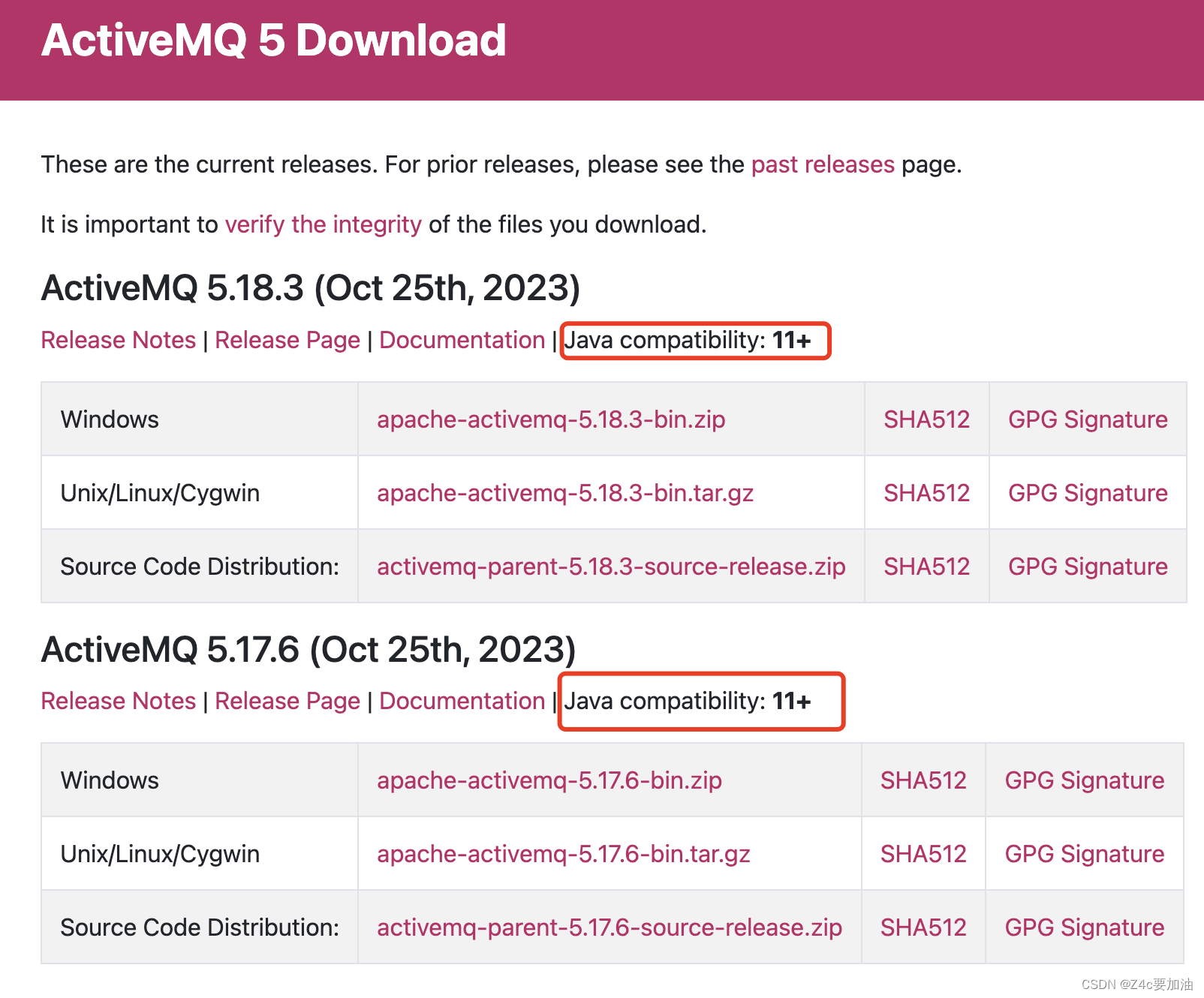
Apache ActiveMQ (版本 < 5.18.3) (CNVD-2023-69477)RCE修复方案/缓解方案
一、漏洞描述 Apache ActiveMQ 是美国阿帕奇(Apache)基金会的一套开源的消息中间件,它支持 Java 消息服务、集群、Spring Framework 等。 二、漏洞成因 ActiveMQ 默认开放了 61616 端口用于接收 OpenWire 协议消息,由于针对异常…...
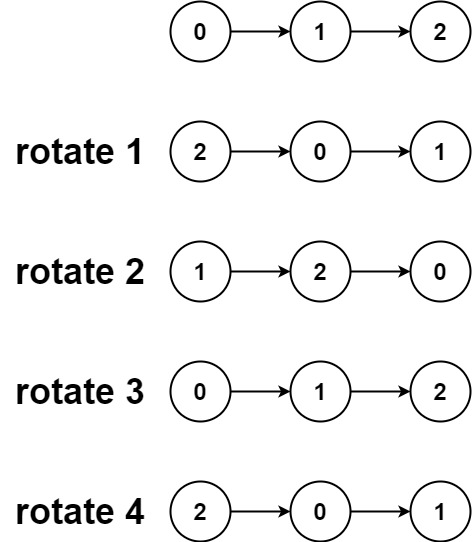
61. 旋转链表、Leetcode的Python实现
博客主页:🏆李歘歘的博客 🏆 🌺每天不定期分享一些包括但不限于计算机基础、算法、后端开发相关的知识点,以及职场小菜鸡的生活。🌺 💗点关注不迷路,总有一些📖知识点&am…...
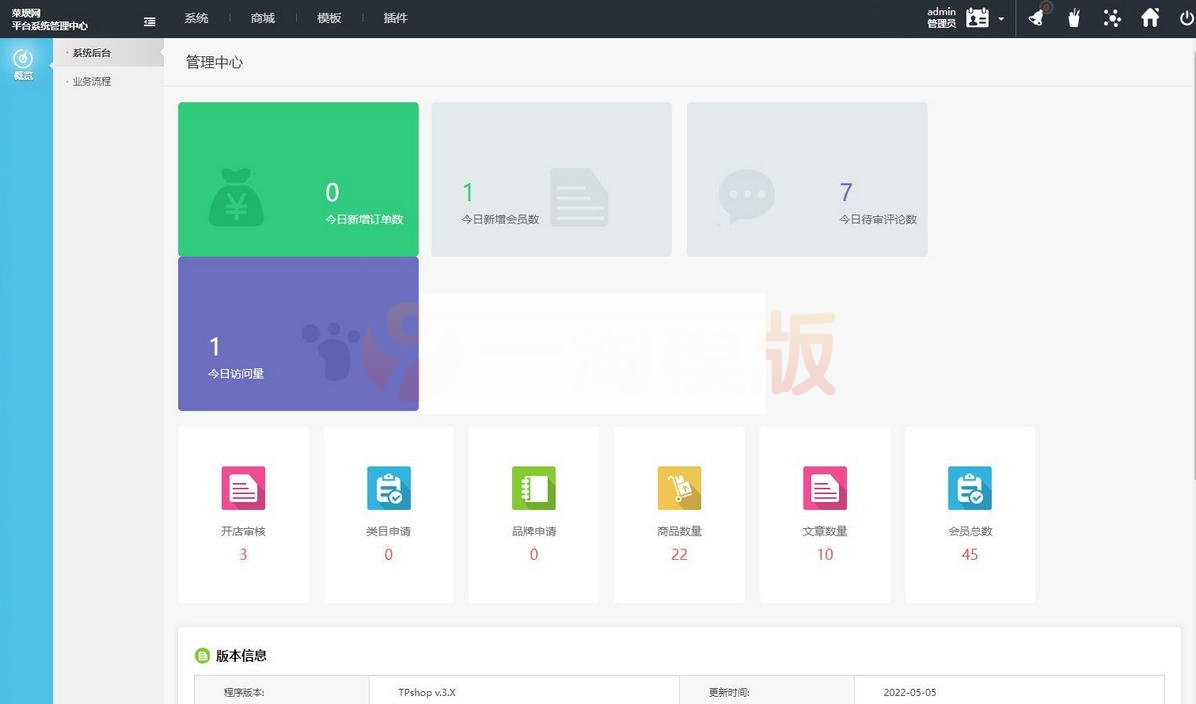
基于tpshop开发多商户源码支持手机端+商家+门店 +分销+淘宝数据导入+APP+可视化编辑
tpshop多商户源码,tpshop商城源码,tpshop b2b2c源码-支持手机端商家门店 分销淘宝数据导入APP可视化编辑 tpshop商城源码算是 thinkphp框架里做的比较早 比较好的源码了,写法简明 友好面向程序猿。 这是一款前几年的版本 虽然后台看着好了些,丝毫不影响…...
ElasticSearch深度解析入门篇:高效搜索解决方案的介绍与实战案例讲解,带你避坑
ElasticSearch深度解析入门篇:高效搜索解决方案的介绍与实战案例讲解,带你避坑 1.Elasticsearch 产生背景 大规模数据如何检索 如:当系统数据量上了 10 亿、100 亿条的时候,我们在做系统架构的时候通常会从以下角度去考虑问题&a…...
HTML简单实现v-if与v-for与v-model
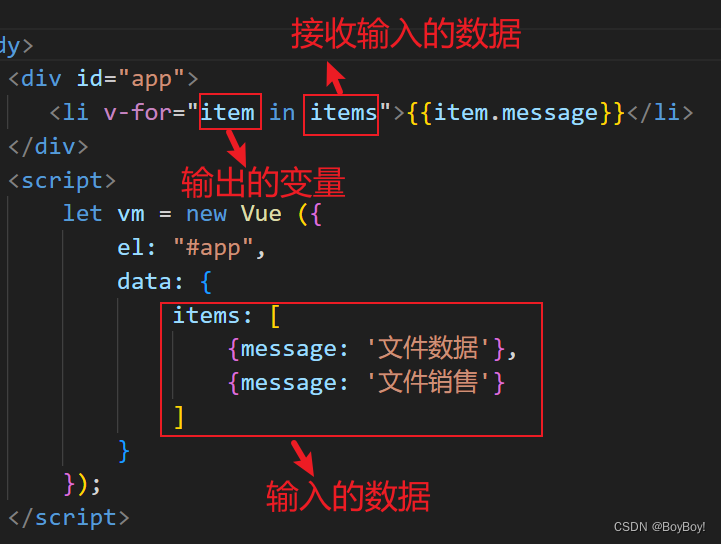
Vue启动!! 首先VIewModel将View和Model连接一起,Model的数据改变View的数据也变 使用Visual Studio Code 启动Vue需要vue.js插件和导入CDN(包) vue.js插件:CTRL shift x 在搜索栏搜 索vue.js安装即可 CDN: http…...

【学习笔记】[PA2021] Fiolki 2
Part 1 前置知识:LGV引理 摘抄自oi-wiki: L G V LGV LGV引理可以用来处理有向无环图上不相交路径计数等问题。 基本定义: w ( P ) w(P) w(P)表示 P P P这条路径上所有边的 边权之积 。(路径计数时,可以将边权都设为…...

计算1到100的和
一、不好的写法 public static void main(String[] args) {int sum 0;int n 100;for (int i 1; i < n; i) {sum i;}System.out.println("sum" sum);}1.定义两个整型变量; 2.执行100次加法运算; 3.打印结果到控制台; 二、好…...

C++下OpenMP耗时统计
在C中,如果你使用OpenMP进行并行计算,你可以使用omp_get_wtime()函数来测量代码段的执行时间。这个函数返回一个double类型的值,表示从某一固定点到当前时间的秒数。因此,你可以在代码的开始和结束点分别调用这个函数,…...

PTA 函数题(C语言)-- 阶乘计算升级版
题目title: 阶乘计算升级版 题目作者: 陈越 浙江大学 本题要求实现一个打印非负整数阶乘的函数。 函数接口定义: void Print_Factorial ( const int N ); 其中N是用户传入的参数,其值不超过1000。如果N是非负整数&#…...
内网穿透入门
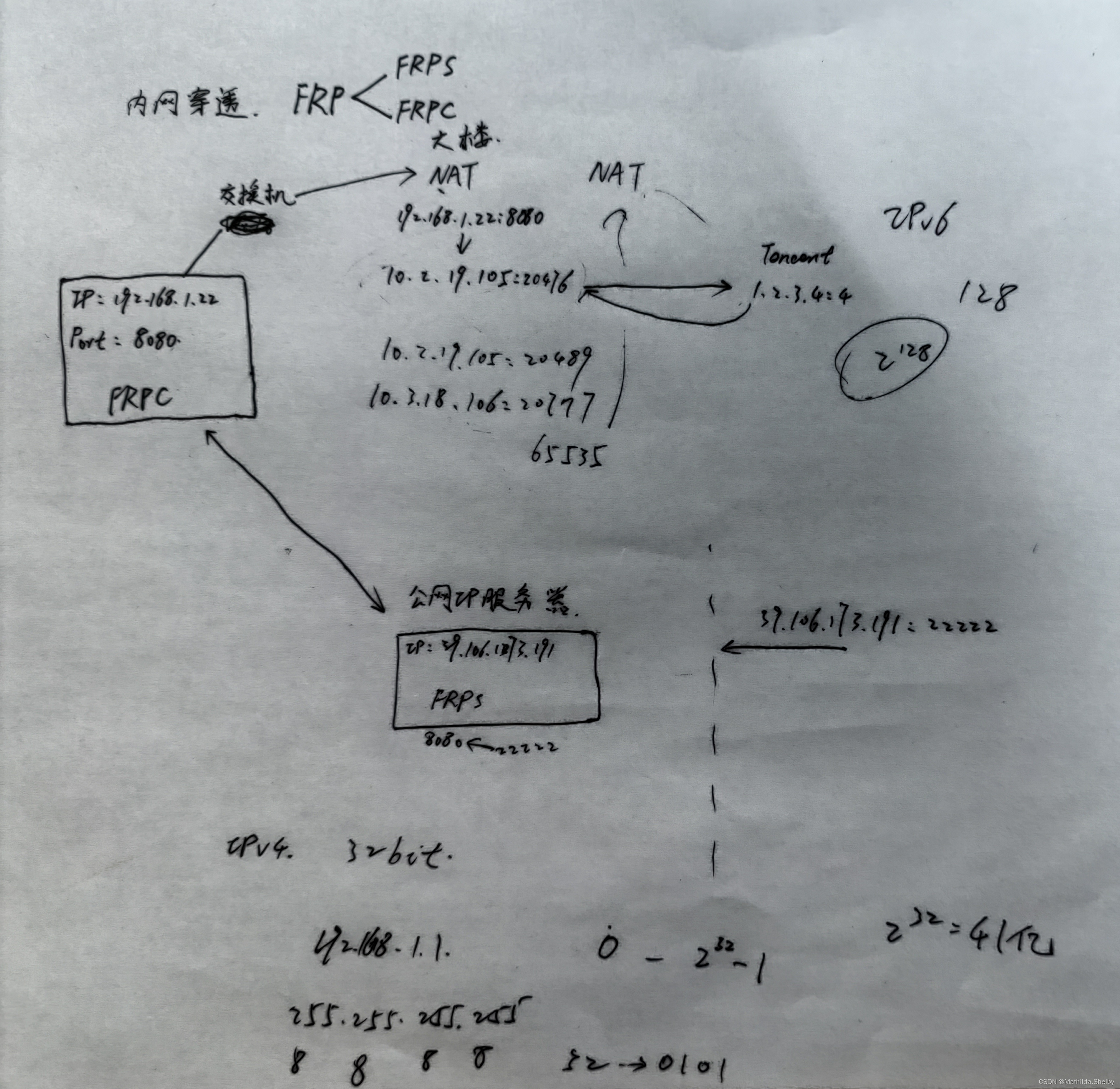
内网穿透 内网穿透(英文:Port Forwarding)是一种网络技术,用于将公共互联网(外网)的请求转发到私有局域网(内网)中的特定设备或服务。在许多情况下,设备或服务位于一个局…...

Pickle pyhton反序列化
参考文章 Python pickle反序列化浅析 Pickle包含四种方法 pickle.dump(obj, file) 将obj对象进行封存,即序列化,然后写入到file文件中 注:这里的file需要以wb打开(二进制可写模式) pickle.load(file) 将file这个文件进行解封,即反序列化 …...

动静分离技术
一、HAproxy 动静分离 1、概念: HAproxy 动静分离技术是一种用于优化 Web 服务器性能和提高用户体验的策略,它通过将动态内容和静态内容分别路由到不同的后端服务器来实现,减轻服务器负载,提高网站的响应速度。 动态内容包括由…...
STM32单片机智能小车一PWM方式实现小车调速和转向
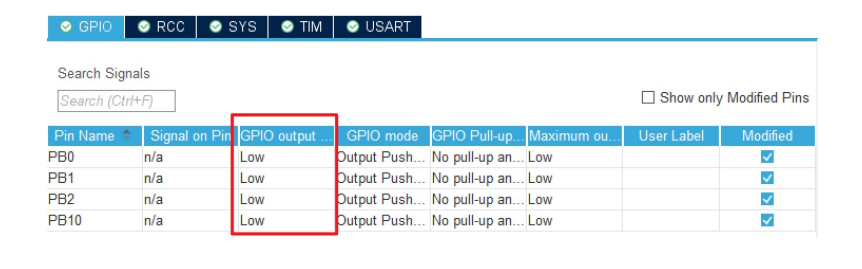
目录 1. 电机模块开发 2. 让小车动起来 3. 串口控制小车方向 4. 如何进行小车PWM调速 5. PWM方式实现小车转向 1. 电机模块开发 L9110s概述 接通VCC,GND 模块电源指示灯亮, 以下资料来源官方,具体根据实际调试 IA1输入高电平ÿ…...
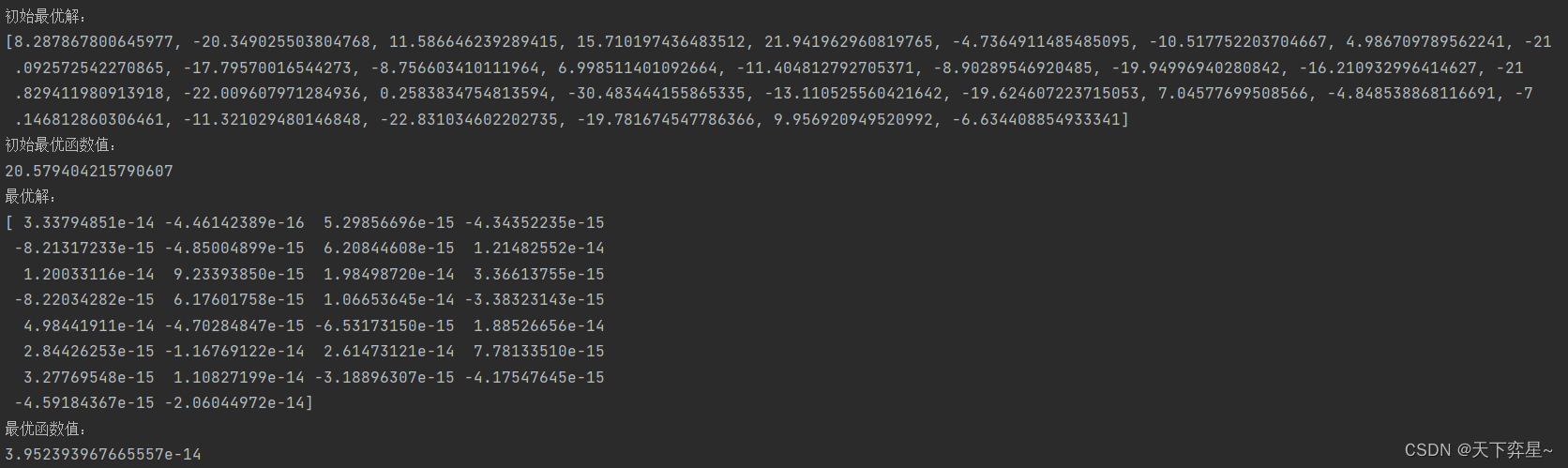
灰狼优化算法(GWO)python
目录 一、灰狼优化算法的python实现 二、灰狼优化算法与遗传算法的对比分析(python) 2.1 GWO1.py 2.2 GA1.py 2.3 GWO_vs_GA.py 2.4 运行结果 三、基于莱维飞行改进的灰狼优化算法的python实现 一、灰狼优化算法的python实现 import numpy as …...
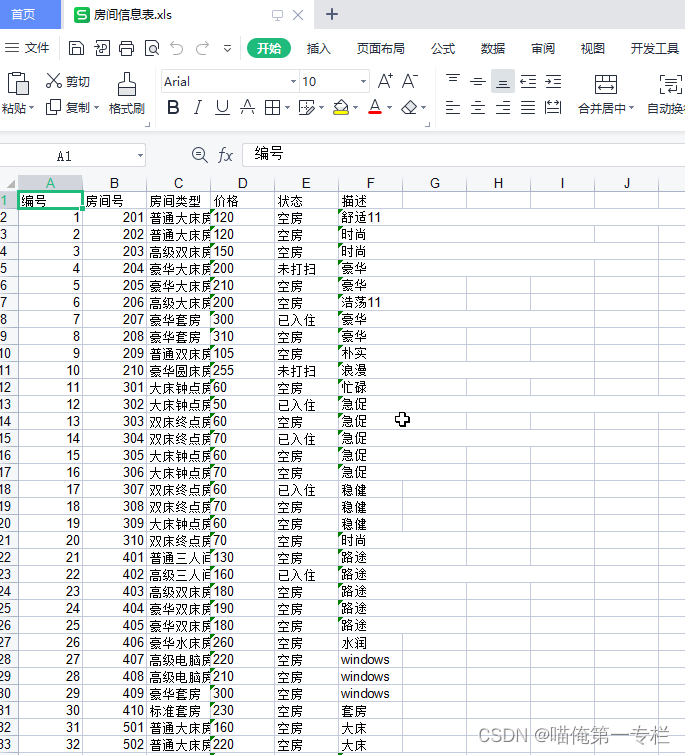
项目知识点总结-住房图片信息添加-Excel导出
(1)住房信息添加 Controller: RequestMapping("/add")public String add(Home home, Model model) throws IOException{String sqlPath null;//定义文件保存的本地路径String localPath"D:\\AnZhuang\\Java项目\\选题\\Xin-…...

第三届iEnglish全国ETP大赛决赛即将启动
如今,寓教于乐的学习方式越来越受到家长和孩子的欢迎,“玩中学”成为一种既能培养兴趣又有助于孩子成长的学习趋势。 以“玩转英语,用iEnglish”为活动主题的第三届全国ETP大赛即将于本周五(11月3日)迎来总决赛的抽签仪式。据主办方iEnglish智能英语学习解决方案相关负责人称,…...
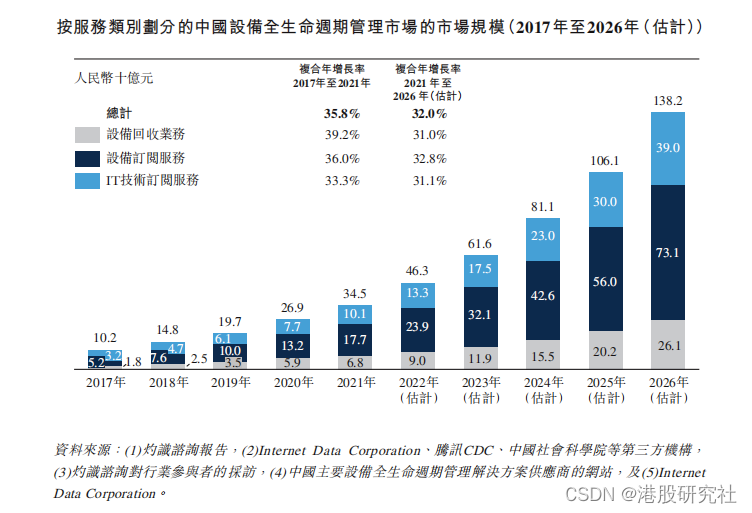
创造产业链协同优势后,凌雄科技在DaaS行业转动成长飞轮
企业服务领域,一直存在一种共识:做好很难,但一旦服务模式跑通了,得到了市场的认可,要滚起雪球就会事半功倍。 重资产、重运营的DaaS(设备及服务)赛道,是个非常典型的细分领域。在这…...

【protobuf】protobuf自定义数据格式,CMake编译C++文件读写自定义数据
protobuf自定义数据格式,CMake编译文件读写自定义数据 1.protobuf安装2.定义.proto文件3.编写main.cpp4.编写CMAkeLists配置文件5.运行 1.protobuf安装 protobuf库链接 2.定义.proto文件 新建一个Person.proto文件和一个Animal.proto文件,内容如下&…...

解决:http://localhost:8080 不在以下 request 合法域名列表中
在搭建资源服务器时,遇到了微信开发者工具中无法访问本地资源服务器的情况,报错如下: 参考一篇博文的方法,完美解决 【解决】http://localhost:8080 不在以下 request 合法域名列表中_localhost不在以下 request 合法域名列表中-…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
