【学习笔记】[PA2021] Fiolki 2
Part 1
前置知识:LGV引理
摘抄自oi-wiki:
L G V LGV LGV引理可以用来处理有向无环图上不相交路径计数等问题。
基本定义: w ( P ) w(P) w(P)表示 P P P这条路径上所有边的 边权之积 。(路径计数时,可以将边权都设为 1 1 1)
e ( u , v ) e(u,v) e(u,v)表示 u u u到 v v v的每一条路径 P P P的 w ( P ) w(P) w(P)之和,即 e ( u , v ) = ∑ P : u → v w ( P ) e(u,v)=\sum_{P:u\to v}w(P) e(u,v)=∑P:u→vw(P)。(注意这里的 P P P都是简单路径)
设起点集合为 A A A,终点集合为 B B B,大小均为 n n n。
一组 A → B A\to B A→B的不相交路径 S S S: S i S_i Si时一条从 A i A_i Ai到 B σ ( S ) i B_{\sigma(S)_i} Bσ(S)i的路径(其中 σ ( S ) \sigma(S) σ(S)是一个排列),对于任意 i ≠ j i\ne j i=j, S i S_i Si和 S j S_j Sj没有公共结点。记 t ( σ ) t(\sigma) t(σ)表示排列 σ \sigma σ的逆序对个数。
引理:
M = [ e ( A 1 , B 1 ) e ( A 1 , B 2 ) ⋯ e ( A 1 , B n ) e ( A 2 , B 1 ) e ( A 2 , B 2 ) ⋯ e ( A 2 , B n ) ⋮ ⋮ ⋱ ⋮ e ( A n , B 1 ) e ( A n , B 2 ) ⋯ e ( A n , B n ) ] M=\begin{bmatrix} e(A_1,B_1)&e(A_1,B_2)&\cdots&e(A_1,B_n)\\ e(A_2,B_1)&e(A_2,B_2)&\cdots&e(A_2,B_n)\\ \vdots&\vdots&\ddots&\vdots\\ e(A_n,B_1)&e(A_n,B_2)&\cdots&e(A_n,B_n) \end{bmatrix} M= e(A1,B1)e(A2,B1)⋮e(An,B1)e(A1,B2)e(A2,B2)⋮e(An,B2)⋯⋯⋱⋯e(A1,Bn)e(A2,Bn)⋮e(An,Bn)
det(M) = ∑ S : A → B ( − 1 ) t ( σ ( S ) ) ∏ i = 1 n ω ( S i ) \text{det(M)}=\sum_{S:A\to B}(-1)^{t(\sigma(S))}\prod_{i=1}^n\omega(S_i) det(M)=S:A→B∑(−1)t(σ(S))i=1∏nω(Si)
其中 ∑ S : A → B \sum_{S:A\to B} ∑S:A→B表示 A → B A\to B A→B的不相交路径组 S S S。
证明考虑行列式的定义,对于相交的路径组可以两两配对且符号相反,因此可以抵消。
对于这道题,题目保证了是有向无环图,因此考虑 L G V LGV LGV引理。
显然,将每条边随机赋一个权值后,就可以直接通过行列式非零来判断是否存在不相交路径。
对于区间 [ l , r ] [l,r] [l,r],由于并不确定被选出的 i i i个位置,因此考虑对于每个位置构造一个 k k k维向量,答案即为从 [ l , r ] [l,r] [l,r]中选出的极大线性无关向量组的大小。路径权值之和可以通过拓扑排序求出。
这样,我们从左往右扫描线,维护一个线性基,如果线性相关了就把编号最小的基替换掉,将剩下的基的编号排序从小到大排序后就能知道每个区间对应的基的大小。
复杂度 O ( n k 2 + m k ) O(nk^2+mk) O(nk2+mk)。
注意线性基的实现方式。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define fi first
#define se second
#define db double
#define inf 0x3f3f3f3f
using namespace std;
const int mod=1e9+7;
const int N=1e5+5;
int n,m,K,du[N],vs[N];
ll a[N][55];
mt19937 gen(114514);
vector<pair<int,int>>G[N];
queue<int>Q;
void add(ll &x,ll y){x=(x+y)%mod;
}
ll f[55][55];
int id[55];
ll res[55];
ll fpow(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
ll g[65];
void ins(int x){for(int i=1;i<=K;i++)g[i]=a[x][i];for(int i=1;i<=K;i++){if(g[i]){if(f[i][i]==0){for(int j=i;j<=K;j++)f[i][j]=g[j];id[i]=x;return;}if(x>id[i]){swap(x,id[i]);for(int j=i;j<=K;j++)swap(f[i][j],g[j]);}ll tmp=g[i]*fpow(f[i][i])%mod;for(int j=i;j<=K;j++)g[j]=(g[j]-f[i][j]*tmp)%mod;}}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m>>K;for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y,z=gen()%mod;G[x].pb({y,z}),du[y]++;}for(int i=1;i<=K;i++){a[i][i]=1;}for(int i=1;i<=n;i++){if(!du[i])Q.push(i);}while(Q.size()){int u=Q.front();Q.pop();vs[u]=1;for(auto e:G[u]){int v=e.fi,w=e.se;for(int i=1;i<=K;i++)add(a[v][i],a[u][i]*w);if(--du[v]==0)Q.push(v);}}for(int i=K+1;i<=n;i++){if(vs[i])ins(i);vector<int>vec;for(int j=1;j<=K;j++)if(id[j])vec.pb(id[j]);sort(vec.begin(),vec.end());int l=K,sz=vec.size();for(int j=0;j<sz;j++){res[sz-j]+=vec[j]-l;l=vec[j];}res[0]+=i-l;}for(int i=0;i<=K;i++)cout<<res[i]<<"\n";
}
相关文章:

【学习笔记】[PA2021] Fiolki 2
Part 1 前置知识:LGV引理 摘抄自oi-wiki: L G V LGV LGV引理可以用来处理有向无环图上不相交路径计数等问题。 基本定义: w ( P ) w(P) w(P)表示 P P P这条路径上所有边的 边权之积 。(路径计数时,可以将边权都设为…...

计算1到100的和
一、不好的写法 public static void main(String[] args) {int sum 0;int n 100;for (int i 1; i < n; i) {sum i;}System.out.println("sum" sum);}1.定义两个整型变量; 2.执行100次加法运算; 3.打印结果到控制台; 二、好…...

C++下OpenMP耗时统计
在C中,如果你使用OpenMP进行并行计算,你可以使用omp_get_wtime()函数来测量代码段的执行时间。这个函数返回一个double类型的值,表示从某一固定点到当前时间的秒数。因此,你可以在代码的开始和结束点分别调用这个函数,…...

PTA 函数题(C语言)-- 阶乘计算升级版
题目title: 阶乘计算升级版 题目作者: 陈越 浙江大学 本题要求实现一个打印非负整数阶乘的函数。 函数接口定义: void Print_Factorial ( const int N ); 其中N是用户传入的参数,其值不超过1000。如果N是非负整数&#…...
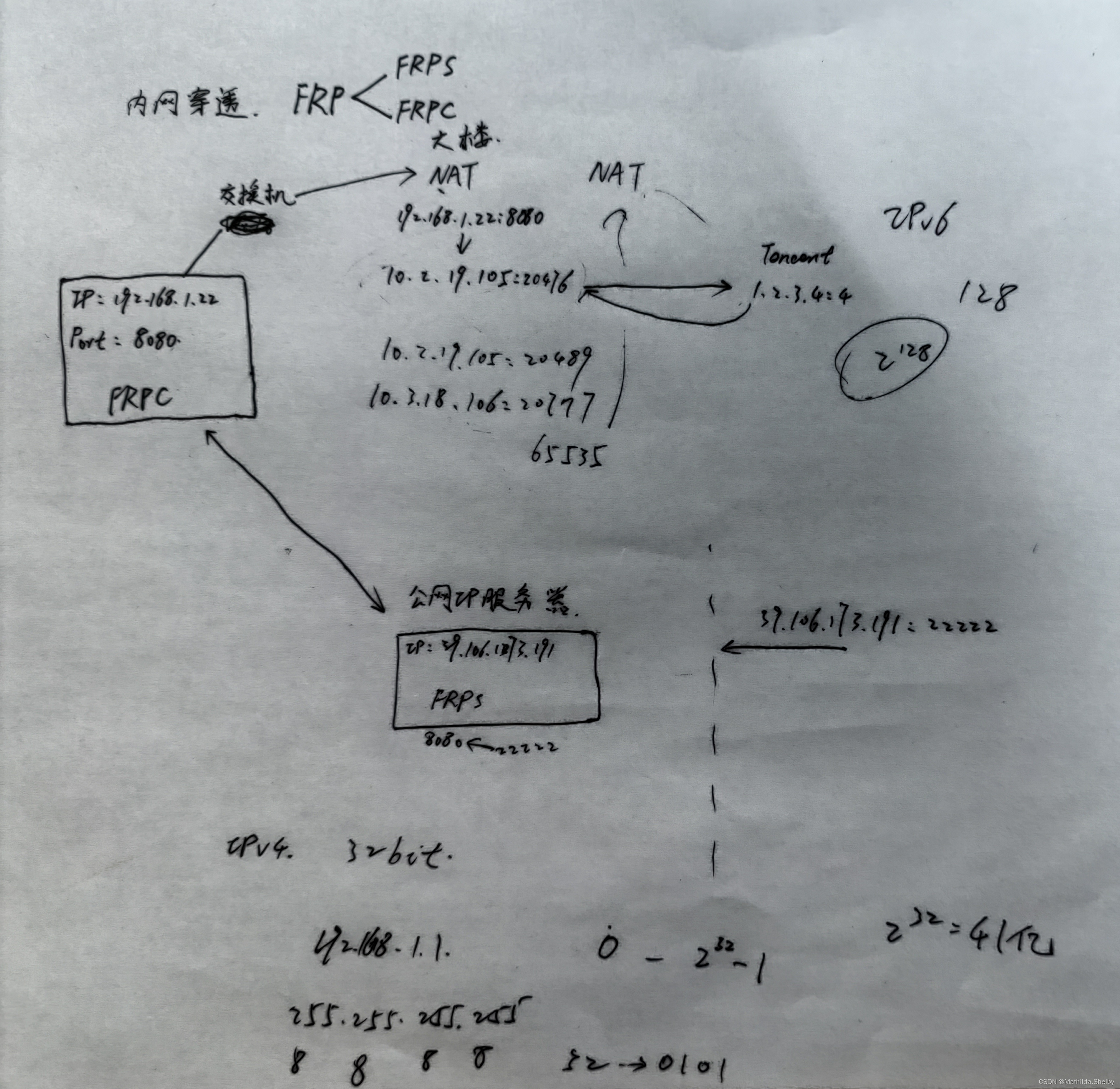
内网穿透入门
内网穿透 内网穿透(英文:Port Forwarding)是一种网络技术,用于将公共互联网(外网)的请求转发到私有局域网(内网)中的特定设备或服务。在许多情况下,设备或服务位于一个局…...

Pickle pyhton反序列化
参考文章 Python pickle反序列化浅析 Pickle包含四种方法 pickle.dump(obj, file) 将obj对象进行封存,即序列化,然后写入到file文件中 注:这里的file需要以wb打开(二进制可写模式) pickle.load(file) 将file这个文件进行解封,即反序列化 …...

动静分离技术
一、HAproxy 动静分离 1、概念: HAproxy 动静分离技术是一种用于优化 Web 服务器性能和提高用户体验的策略,它通过将动态内容和静态内容分别路由到不同的后端服务器来实现,减轻服务器负载,提高网站的响应速度。 动态内容包括由…...
STM32单片机智能小车一PWM方式实现小车调速和转向
目录 1. 电机模块开发 2. 让小车动起来 3. 串口控制小车方向 4. 如何进行小车PWM调速 5. PWM方式实现小车转向 1. 电机模块开发 L9110s概述 接通VCC,GND 模块电源指示灯亮, 以下资料来源官方,具体根据实际调试 IA1输入高电平ÿ…...
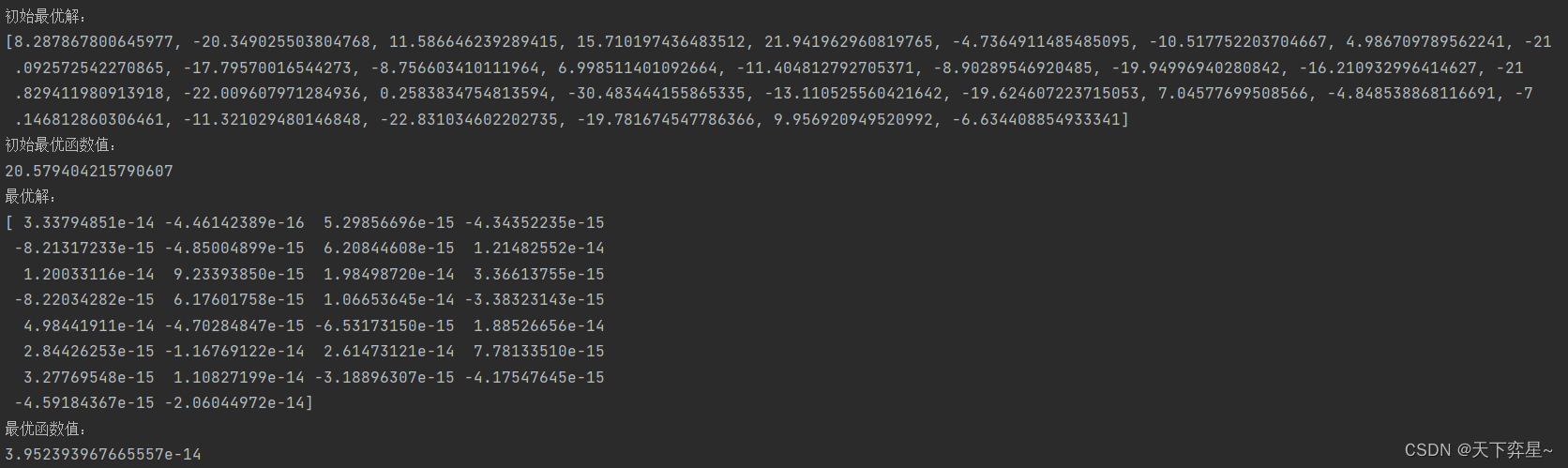
灰狼优化算法(GWO)python
目录 一、灰狼优化算法的python实现 二、灰狼优化算法与遗传算法的对比分析(python) 2.1 GWO1.py 2.2 GA1.py 2.3 GWO_vs_GA.py 2.4 运行结果 三、基于莱维飞行改进的灰狼优化算法的python实现 一、灰狼优化算法的python实现 import numpy as …...
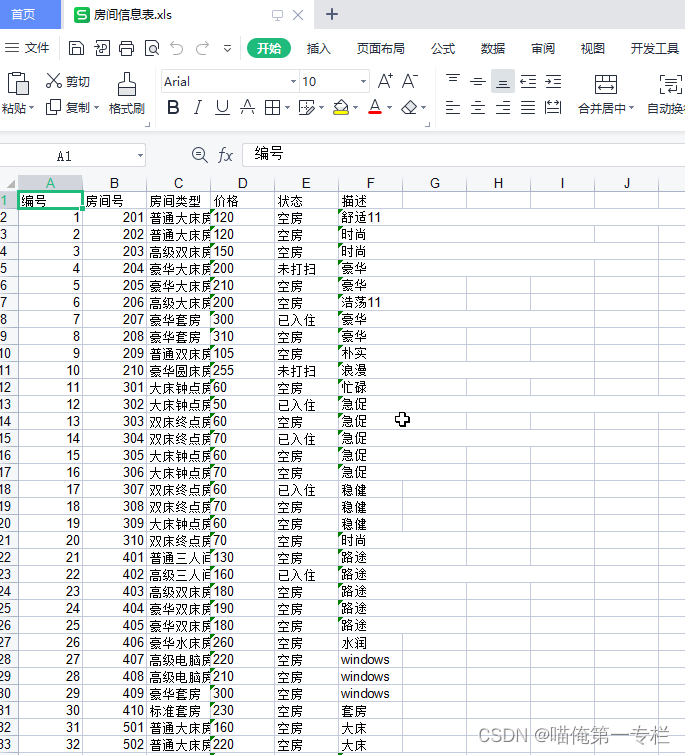
项目知识点总结-住房图片信息添加-Excel导出
(1)住房信息添加 Controller: RequestMapping("/add")public String add(Home home, Model model) throws IOException{String sqlPath null;//定义文件保存的本地路径String localPath"D:\\AnZhuang\\Java项目\\选题\\Xin-…...

第三届iEnglish全国ETP大赛决赛即将启动
如今,寓教于乐的学习方式越来越受到家长和孩子的欢迎,“玩中学”成为一种既能培养兴趣又有助于孩子成长的学习趋势。 以“玩转英语,用iEnglish”为活动主题的第三届全国ETP大赛即将于本周五(11月3日)迎来总决赛的抽签仪式。据主办方iEnglish智能英语学习解决方案相关负责人称,…...
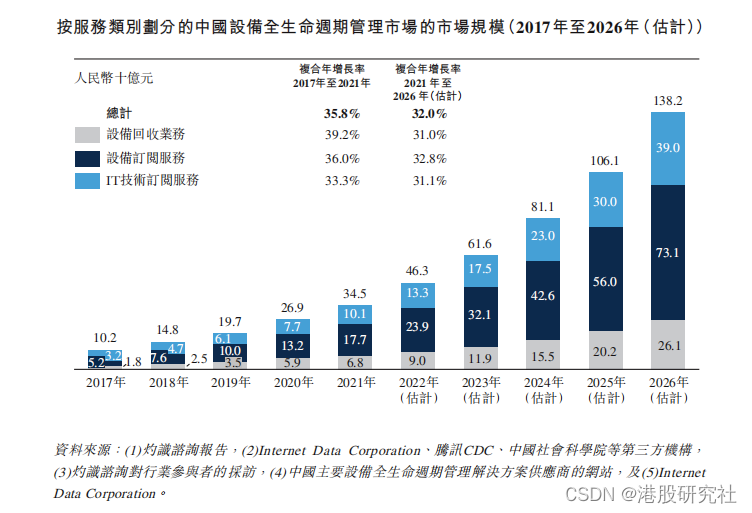
创造产业链协同优势后,凌雄科技在DaaS行业转动成长飞轮
企业服务领域,一直存在一种共识:做好很难,但一旦服务模式跑通了,得到了市场的认可,要滚起雪球就会事半功倍。 重资产、重运营的DaaS(设备及服务)赛道,是个非常典型的细分领域。在这…...

【protobuf】protobuf自定义数据格式,CMake编译C++文件读写自定义数据
protobuf自定义数据格式,CMake编译文件读写自定义数据 1.protobuf安装2.定义.proto文件3.编写main.cpp4.编写CMAkeLists配置文件5.运行 1.protobuf安装 protobuf库链接 2.定义.proto文件 新建一个Person.proto文件和一个Animal.proto文件,内容如下&…...

解决:http://localhost:8080 不在以下 request 合法域名列表中
在搭建资源服务器时,遇到了微信开发者工具中无法访问本地资源服务器的情况,报错如下: 参考一篇博文的方法,完美解决 【解决】http://localhost:8080 不在以下 request 合法域名列表中_localhost不在以下 request 合法域名列表中-…...

Linux普通用户提权(sudo)
文章目录 Linux普通用户提权(sudo)1、在sudoers文件添加普通用户2、测试 Linux普通用户提权(sudo) 1、在sudoers文件添加普通用户 正常来说,普通用户初始是不具备提权的能力的,比如执行sudo ls会出现报警告…...
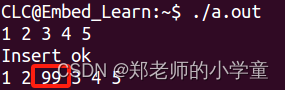
链表指定节点的插入
向现有链表中插入结点,根据插入位置的不同,可分为以下 3 种情况: 插入到链表的头部,作为新的链表中第一个存有数据的结点(又称为”首元结点”);插入到链表中某两个结点之间的位置;插…...

解决问题Conda:CondaValueError: Malformed version string ‘~’ : invalid character(s)
解决问题Conda:CondaValueError: Malformed version string ‘~’ : invalid character(s) 背景 今天使用Conda构建项目运行环境的时候报错::CondaValueError: Malformed version string ‘~’ : invalid character(s) ##报错问题 在安装te…...
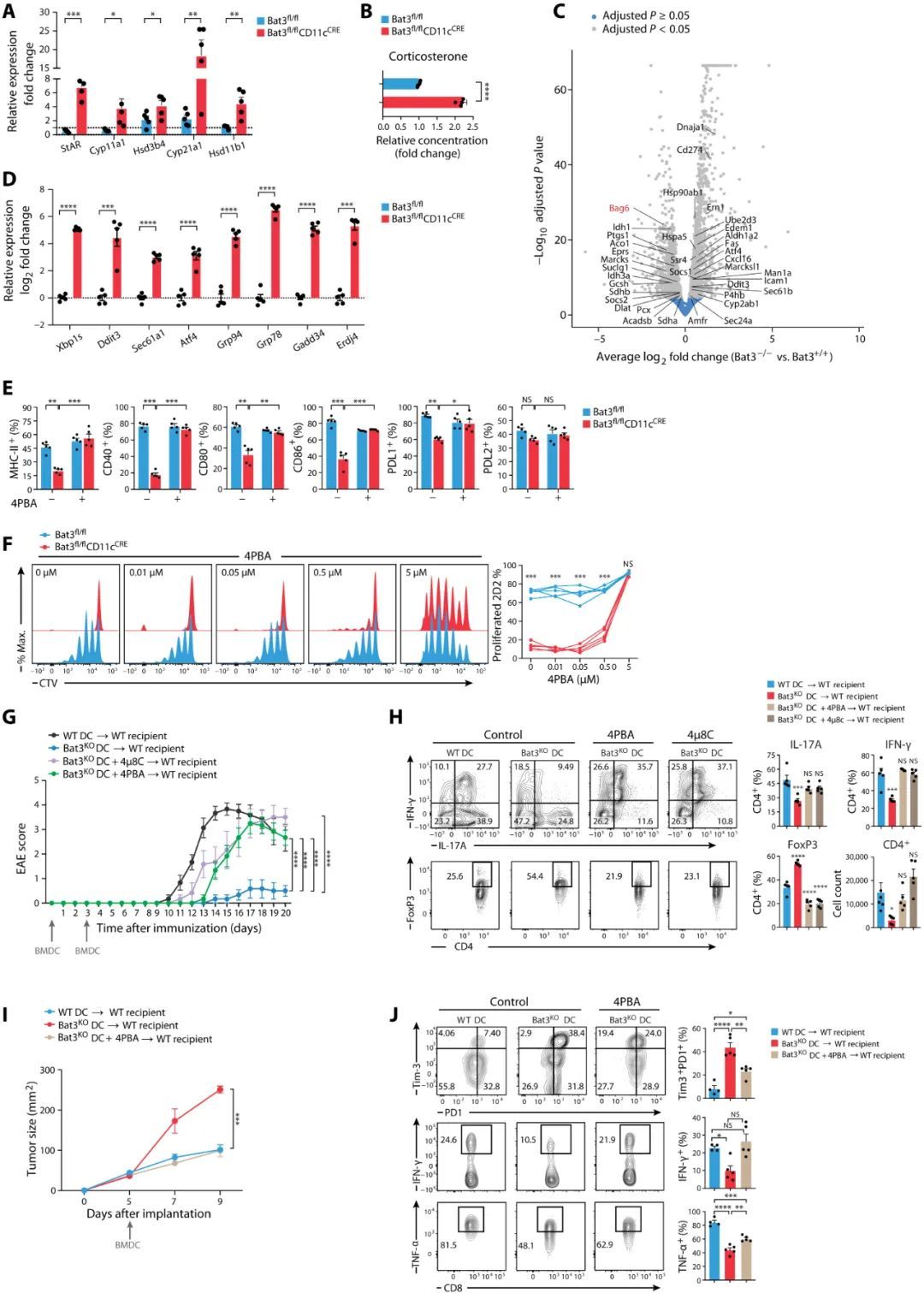
Sci Immunol丨Tim-3 适配器蛋白 Bat3 是耐受性树突状细胞
今天和大家分享一篇发表于2022年3月的文章,题目为“Tim-3 adapter protein Bat3 acts as an endogenous regulator of tolerogenic dendritic cell function”,发表在《Sci Immunol》杂志上。文章主要研究了Tim-3和其适配蛋白Bat3在调节免疫应答中的作用…...
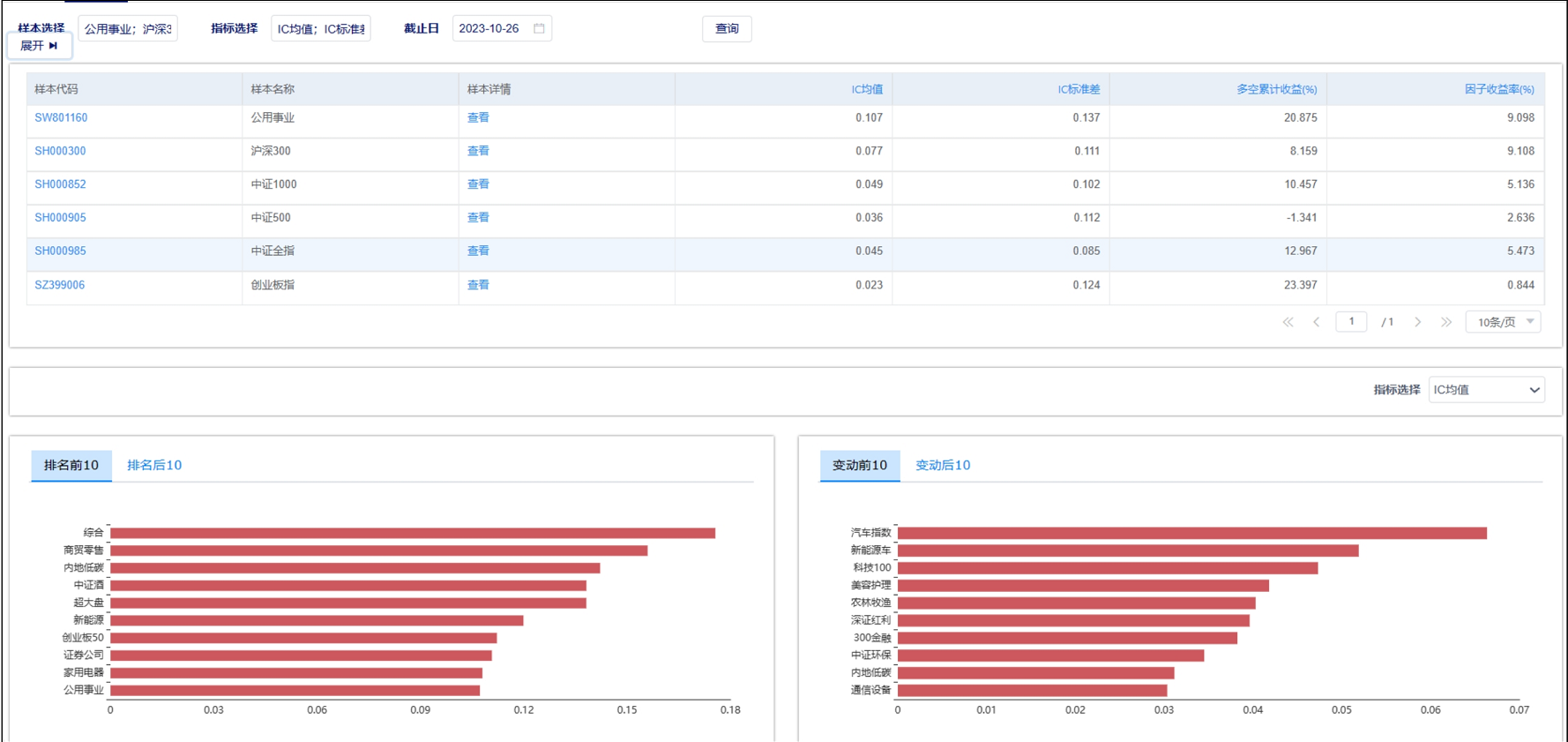
天软特色因子看板(2023.10 第14期)
该因子看板跟踪天软特色因子A05005(近一月单笔流通金额占比(%),该因子为近一个月单笔流通金额占比因子,用以刻画股票在收盘时,主力资金在总交易金额中所占的比重。 今日为该因子跟踪第14期,跟踪其在SW801160 (申万公用事业) 中的表…...
Photoshop(PS)2021版 安装教程(图文教程超详细)
软件:PS版本:2021语言:简体中文大小:2.26G安装环境:Win11/Win10(1809以上版本)硬件要求:CPU2.0GHz 内存4G(或更高,不支持7代以下CPU)下载通道①百度网盘丨64位…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
