逻辑回归
逻辑回归
在分类问题中,要预测的变量y为离散值(y=0~1),逻辑回归模型的输出变量范围始终在 0 和 1 之间。
训练集为
{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\} {(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}
输入
x∈[x0x1⋮xn]其中x0=1,y∈{0,1}x \in \left[ \begin{matrix} x_0 \\ x_1 \\ \vdots \\ x_n \\ \end{matrix} \right] 其中x_0=1,y \in \{0,1\} x∈x0x1⋮xn其中x0=1,y∈{0,1}
逻辑回归模型的假设是:
hθ(x)=g(θTX)h_\theta(x)=g(\theta^{\mathrm T}X) hθ(x)=g(θTX)
XXX为特征变量,g(.)g(.)g(.)为逻辑函数
g(z)=11+e−zg(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZEzwMmHR-1677396732146)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230223113840999.png)]](https://img-blog.csdnimg.cn/2cfa73ab36154191ad8abbf39a45a9ee.png)
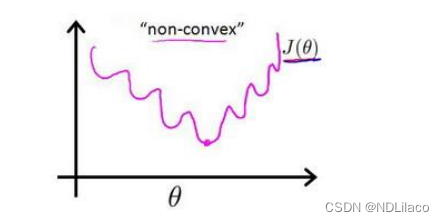
如果对于逻辑回归沿用线性回归的代价函数,此时的代价函数是非凸函数,不利于找局部最优值,
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kpT45RTi-1677396732147)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230223143832677.png)]](https://img-blog.csdnimg.cn/1cd23d98053d4355bad4305c6523b8b0.png)
逻辑回归的代价函数为:
J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))J(\theta)=\frac{1}{m}\sum^m_{i=1}{Cost(h_{\theta}(x^{(i)}),y^{(i)})} J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))
Cost(hθ(x),y)={−log(hθ(x)),ify=1−log(1−hθ(x)),ify=0Cost(h_{\theta}(x),y)=\left\{ \begin{matrix} -log(h_{\theta}(x)) ,if\quad y=1\\ -log(1-h_{\theta}(x)) ,if\quad y=0 \end{matrix} \right. Cost(hθ(x),y)={−log(hθ(x)),ify=1−log(1−hθ(x)),ify=0
Cost(hθ(x),y)=−y⋅log(hθ(x))−(1−y)⋅log(1−hθ(x))Cost(h_{\theta}(x),y)=-y\cdot log(h_{\theta}(x))-(1-y)\cdot log(1-h_{\theta}(x)) Cost(hθ(x),y)=−y⋅log(hθ(x))−(1−y)⋅log(1−hθ(x))
当实际的 𝑦 = 1 且hθ(𝑥)ℎ_{\theta}(𝑥)hθ(x)也为 1 时,误差为 0,
当 𝑦 = 1 但hθ(𝑥)ℎ_{\theta}(𝑥)hθ(x)不为 1 时,误差随着hθ(𝑥)ℎ_{\theta}(𝑥)hθ(x)变小而变大;
当实际的 𝑦 = 0 且hθ(𝑥)ℎ_{\theta}(𝑥)hθ(x)也为 0 时,误差为 0,
当𝑦 = 0 但hθ(𝑥)ℎ_{\theta}(𝑥)hθ(x)不为 0 时误差随着 hθ(𝑥)ℎ_{\theta}(𝑥)hθ(x)的变大而变大。
利用梯度下降算法
θj:=θj−α∂∂θjJ(θ)\theta_{j}:=\theta_{j}-\alpha\frac{\partial }{\partial \theta_{j}}J(\theta) θj:=θj−α∂θj∂J(θ)
代价函数的导数为
∂∂θjJ(θ)=1m∑i=1m[hθ(x(i))−y(i)]xj(i)\frac{\partial }{\partial \theta_{j}}J(\theta)=\frac{1}{m}\sum_{i=1}^{m}{[h_{\theta}(x^{(i)})-y^{(i)}]}x_j^{(i)} ∂θj∂J(θ)=m1i=1∑m[hθ(x(i))−y(i)]xj(i)
则最终结果为(可同时更新所有的θ\thetaθ)
θj:=θj−α1m∑i=1m[hθ(x(i))−y(i)]xj(i)\theta_{j}:=\theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}{[h_{\theta}(x^{(i)})-y^{(i)}]}x_j^{(i)} θj:=θj−αm1i=1∑m[hθ(x(i))−y(i)]xj(i)
此时的梯度函数跟线性回归不太相同,因为hθ(x)h_\theta(x)hθ(x)不同。
相关文章:
逻辑回归
逻辑回归 在分类问题中,要预测的变量y为离散值(y0~1),逻辑回归模型的输出变量范围始终在 0 和 1 之间。 训练集为 {(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\} {…...
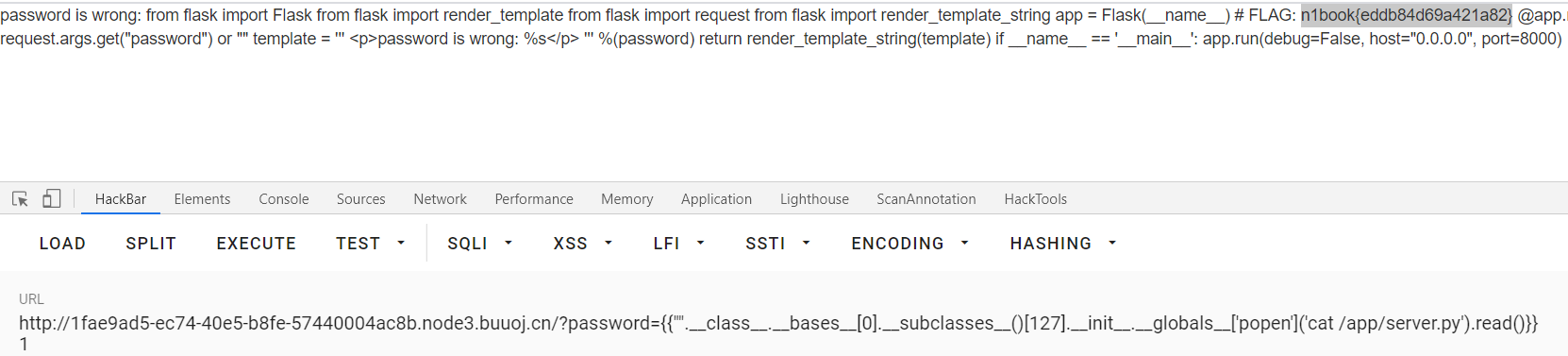
CTFer成长之路之Python中的安全问题
Python中的安全问题CTF 1.Python里的SSRF 题目提示 尝试访问到容器内部的 8000 端口和 url path /api/internal/secret 即可获取 flag 访问url: http://f5704bb3-5869-4ecb-9bdc-58b022589224.node3.buuoj.cn/ 回显如下: 通过提示构造payload&…...
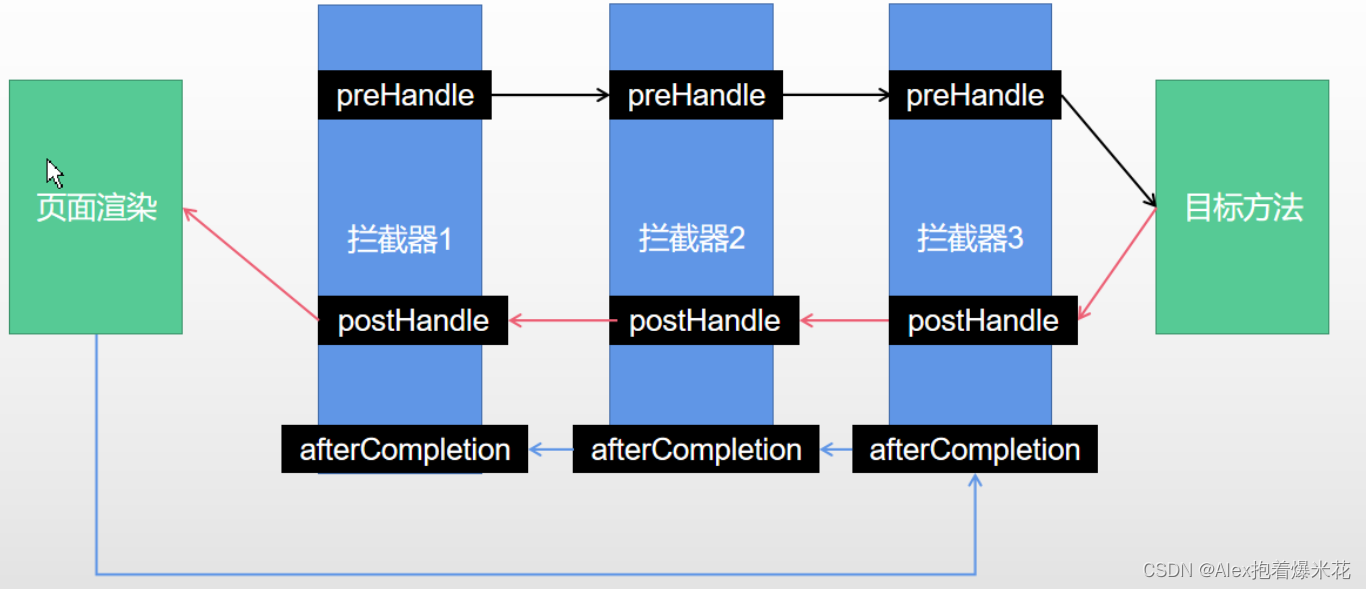
SpringBoot知识快速复习
Spring知识快速复习启动器自动装配ConfigurationImport导入组件Conditional条件装配ImportResource导入Spring配置文件ConfigurationProperties配置绑定Lombok简化开发dev-toolsyaml请求和响应处理静态资源规则与定制化请求处理-Rest映射请求处理-常用参数注解使用请求处理-Ser…...
SpringBoot+React博客论坛系统 附带详细运行指导视频
文章目录一、项目演示二、项目介绍三、项目运行截图四、主要代码一、项目演示 项目演示地址: 视频地址 二、项目介绍 项目描述:这是一个基于SpringBootReact框架开发的博客论坛系统。首先,这是一个前后端分离的项目,文章编辑器…...

C++ primer 之 extern
C primer 之 extern什么是声明什么是定义两者有什么区别ertern的作用什么是声明 就是使得名字为程序所知,一个文件如果想使用别处定义的名字就必须包含对那个名字的声明。 什么是定义 负责创建与名字关联的实体。 两者有什么区别 变量声明和声明都规定了变量的…...
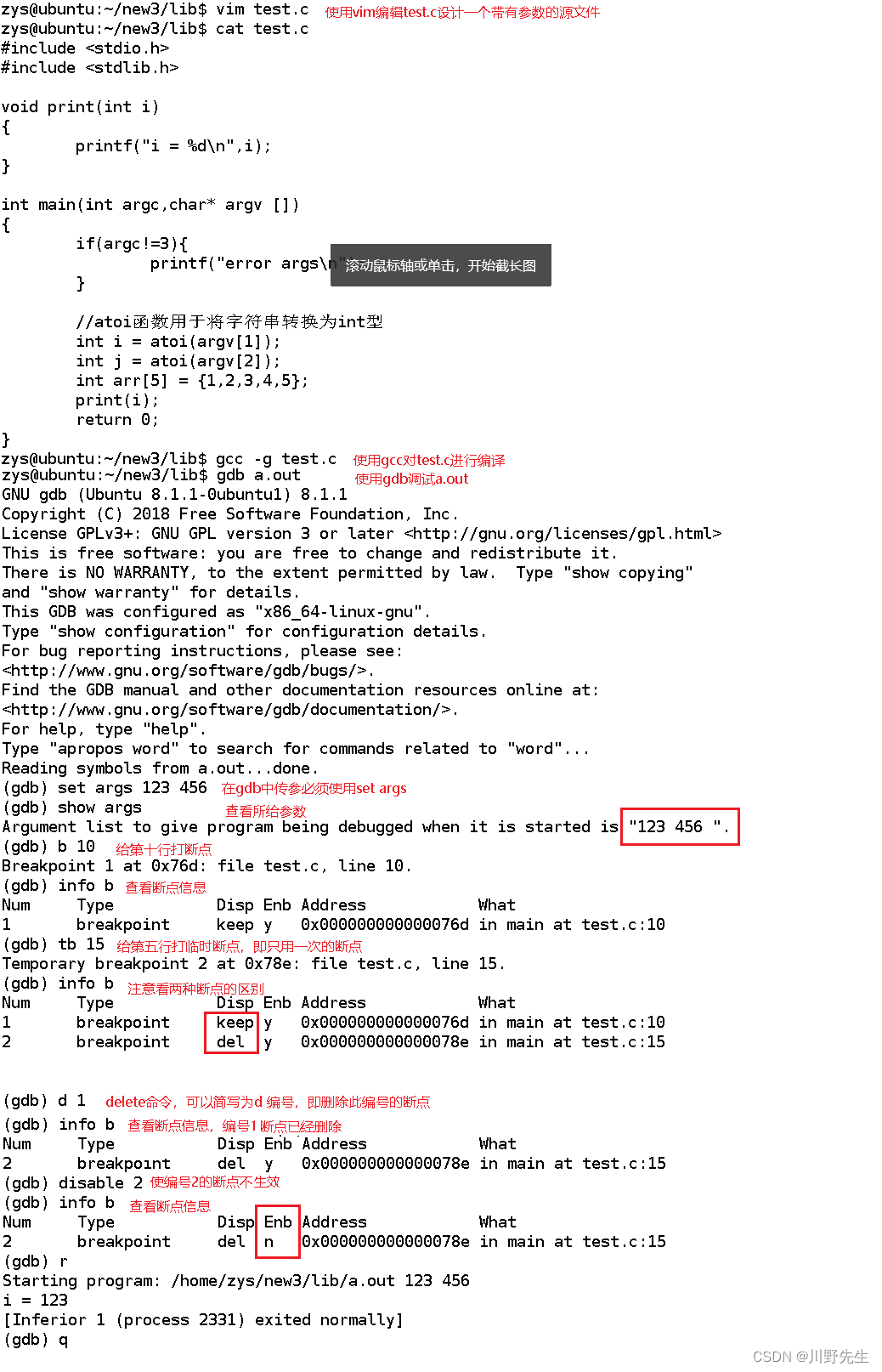
Linux 练习二 (VIM编辑器 + GCC编译器 + GDB调试)
文章目录VIM命令思维导图GCC编译器1、GCC编译文件练习2、静态库动态库制作练习将此函数编译成动态库将此函数编译成静态库GCC优化选项 -OnGDB调试命令练习练习一:编写一个程序,通过gdb调试,使用到gdb的b,n,s࿰…...

python3 连接数据库 mysql PyMysql
python3PyMysql PyMySQL 是在 Python3.x 版本中用于连接 MySQL 服务器的一个库 , 遵循 Python 数据库 API v2.0 规范 。 PyMySQL 安装 pip install PyMySQLPyMySQL 连接数据库 import pymysql pymysql.Connect(hostlocalhost,port 3306,user root,password **…...
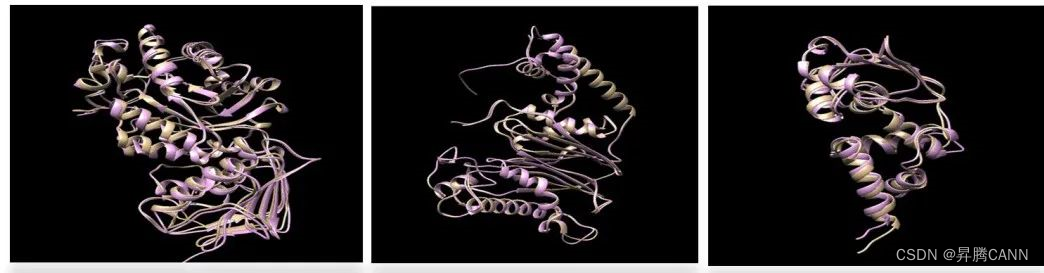
昇腾AI新技能,还能预防猪生病?
国药集团动物保健股份有限公司(简称“国药动保”)是专业从事动物保健产品研发、生产和销售的国家高新技术企业,是国内少数几家具备新产品原创能力的动物保健企业。其中,猪圆环病毒灭活疫苗等市场份额位居行业前列。 “猪圆环病毒…...
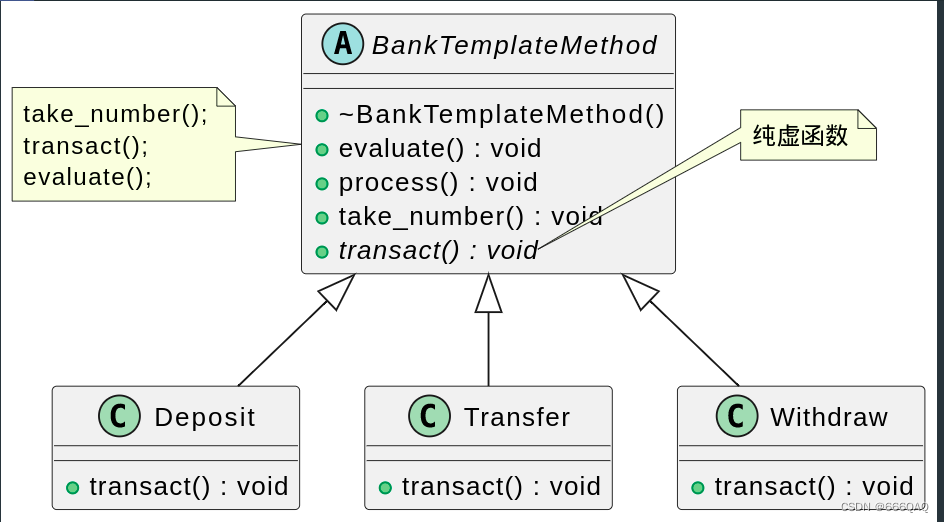
模板方法模式(Template Method)
模式结构图 说明 基本方法是模板方法的组成部分。基本方法分为一下三种: 抽象方法 由抽象类声明,由其具体子类实现。C中就是纯虚函数。 具体方法 由抽象类或具体类声明并实现,子类可以进行覆盖也可以继承。C中是虚函数。 钩子方法 由抽象类…...

C C++ typedef的使用
一、为基本数据类型起别名 typedef int myint; myint x 5; "myint"是"int"的别名,可以使用"myint"来代替"int"声明变量,这个很好理解,但是也很少有人这么用吧。 二、为结构体起别名 …...
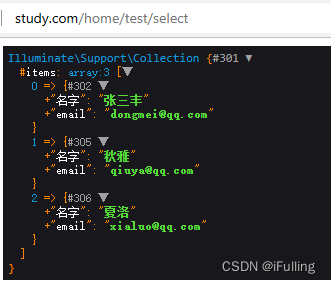
Laravel框架03:DB类操作数据库
Laravel框架03:DB类操作数据库一、概述二、数据表的创建与配置三、增删改操作1. 增加信息2. 修改数据3. 删除数据四、查询操作1. 取出基本数据2. 取出单行数据3. 获取一个字段的值4. 获取多个字段的值5. 排序6. 分页五、执行任意的SQL语句一、概述 按照MVC的架构&a…...

数据结构期末复习总结(前章)
作者的话 作为一名计算机类的学生,我深知数据结构的重要性。在期末复习前,我希望通过这篇博客给大家一些复习建议。希望能帮助大家夯实数据结构的基础知识,并能够更好地掌握数据结构和算法的应用。 一、绪论 数据:信息的载体&am…...
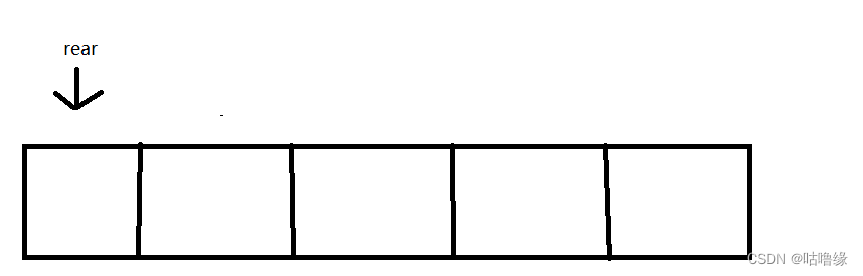
设计环形队列
文章目录1.思路分析1.1队列空满分析1.2出队分析2.循环队列设计1.思路分析 1.1队列空满分析 首先我们假设一个长度为4的环形队列 队头front 队尾rear 当队列为空时 frontrear 当队列满时 frontrear 所以我们无法判断队列是满的或者空的 因此我们多加入一个空间使队列长度为5&am…...

面向对象之-接口鉴权
1 需求 1.1 需求背景 为了保证接口调用的安全性,我们希望设计实现一个接口调用鉴权功能,只有经过认证之后的系统才能调用我们的接口,没有认证过的系统调用我们的接口会被拒绝。 2 需求分析 2.1 基础分析 对于如何做鉴权这样一个问题&…...
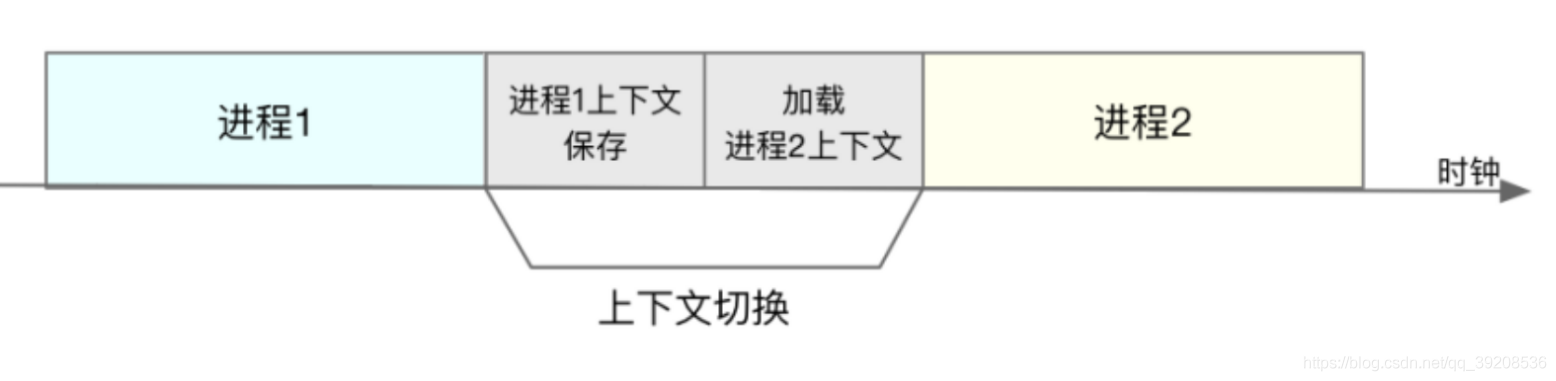
Python 多进程多线程线程池进程池协程
目录 一、线程与进程很简单的介绍 1.1 线程与进程的区别 二、多进程Process 2.1 多进程与多线程的区别 2.2 多进程为啥要使用队列 2.3 控制进程运行顺序 2.3.1 join , 2.3.1 daemon 守护进程 2.4 进程id 2.5 进程 存活状态is_alive() 2.5 实现自定义多…...
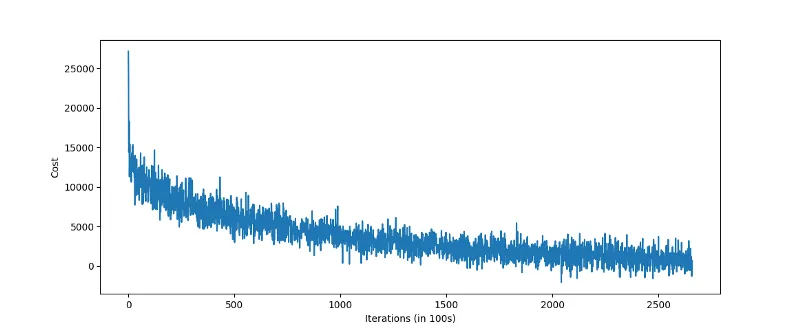
【自然语言处理】基于句子嵌入的文本摘要算法实现
基于句子嵌入的文本摘要算法实现人们在理解了文本的含义后,很容易用自己的话对文本进行总结。但在数据过多、缺乏人力和时间的情况下,自动文本摘要则显得至关重要。一般使用自动文本摘要的原因包括: 减少阅读时间根据摘要,选择自…...
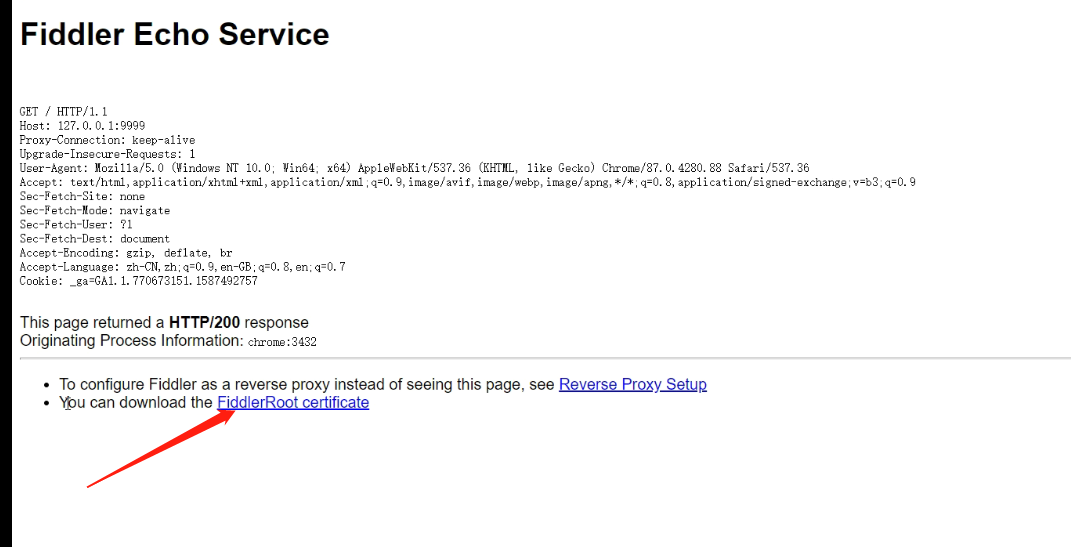
fiddler抓包
一、工具介绍Fiddler是一个通过代理的方式来进行抓包工具,运行时会在本地建立一个代理服务,默认地址:127.0.0.1:8888。Fiddler开启之后,配置本机代理,再打开IE浏览器,IE的PROXY会自动变成127.0.0.1:8888&am…...
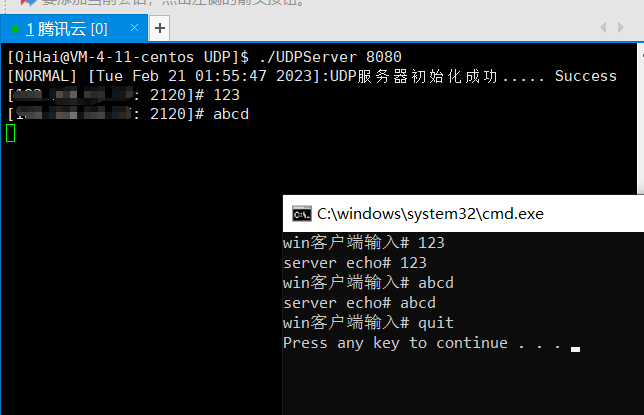
【Linux】网络套接字编程
前言 在掌握一定的网络基础,我们便可以先从代码入手,利用UDP协议/TCP协议进行编写套接字程序,明白网络中服务器端与客户端之间如何进行连接并且通信的。 目录 一、了解源目的IP、端口、网络字节序、套接字 端口号: 套接字&…...
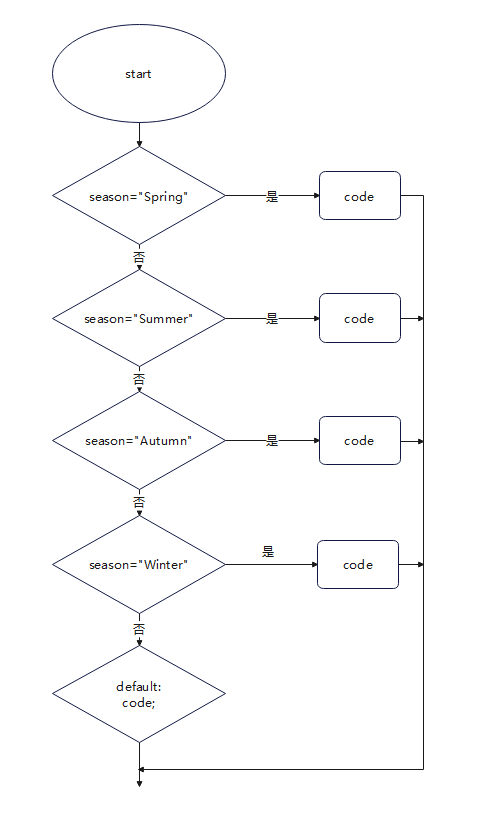
break与continue关键字
1.概述 不知道大家有没有这样一种感受哈,有的时候容易混淆break语句和continue语句的用法,总是模棱两可,不敢确定自己是否使用正确了。正好,我们本篇的重点就是break和continue关键字的用法。 2.使用场景 Java中为啥会诞生break…...
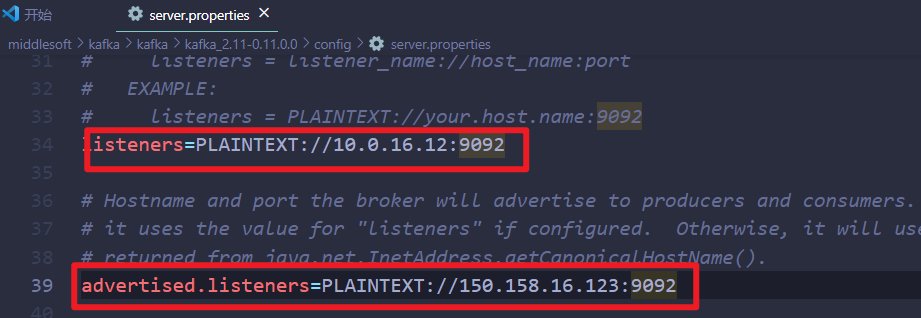
kafka使用入门案例与踩坑记录
每次用到kafka时都会出现各种奇怪的问题,综合实践,下面汇总下主要操作步骤: Docker镜像形式启动 zookeeper启动 docker run -d --name zookeeper -p 2181:2181 -t wurstmeister/zookeeperkafka启动 docker run --name kafka01 -p 9092:909…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
