算法笔记【8】-合并排序算法
文章目录
- 一、前言
- 二、合并排序算法基本原理
- 三、实现步骤
- 四、优缺点分析
一、前言
合并排序算法通过采用分治策略和递归思想,实现了高效、稳定的排序功能。本文将深入探讨合并排序算法的原理、实现步骤,并讨论其优缺点。
二、合并排序算法基本原理
合并排序算法采用了分治策略,将一个大问题分解为若干个小问题,并通过递归地解决这些小问题来达到整体解决的目的。具体而言,合并排序首先将待排序的数组不断划分为两个子数组,直到每个子数组只包含一个元素,然后将这些子数组进行两两合并,同时按照大小顺序排列,最终得到完全有序的数组。
三、实现步骤
以数组为例,其算法流程原理如图所示。

由图可知,合并排序算法的实现步骤可大致分为三步:
- 第一步-》递归划分:将待排序数组不断划分为两个子数组,直到每个子数组只包含一个元素。
- 第二步-》合并操作:将两个有序的子数组合并为一个有序数组,同时按照大小顺序排列。
- 第三步-》重复上述步骤,直到整个数组排序完成。
以下是使用matlab编写的合并排序算法示例代码:
- 合并排序算法函数
%% 合并排序算法函数
function sorted_array = mergeSort(arr)% 检查输入数组是否为空或只有一个元素if length(arr) <= 1sorted_array = arr;return;end% 将输入数组分为两个子数组mid = fix(length(arr)/2);left_array = arr(1:mid);right_array = arr(mid+1:end);% 递归调用mergeSort函数对子数组进行排序left_sorted = mergeSort(left_array);right_sorted = mergeSort(right_array);% 合并两个已排序的子数组sorted_array = merge(left_sorted, right_sorted);
end%% 子数组排序合并函数
function merged_array = merge(arr1, arr2)% 初始化指针和合并后的数组i = 1; j = 1; k = 1;merged_length = length(arr1) + length(arr2);merged_array = zeros(1, merged_length);% 比较两个数组的元素,并按顺序将较小的元素放入合并后的数组中while i <= length(arr1) && j <= length(arr2)if arr1(i) <= arr2(j)merged_array(k) = arr1(i);i = i + 1;elsemerged_array(k) = arr2(j);j = j + 1;endk = k + 1;end% 将剩余的元素复制到合并后的数组中while i <= length(arr1)merged_array(k) = arr1(i);i = i + 1;k = k + 1;endwhile j <= length(arr2)merged_array(k) = arr2(j);j = j + 1;k = k + 1;end
end
- 调用
clc;
clear;
arr = [79,88,70,37,92,6,28,54];
%% 快速排序函数调用
sortedArr= mergeSort(arr);
disp("***********合并排序*****************************");
disp("排序前的数组:");
disp(arr);
disp("排序后的数组:");
disp(sortedArr);
- 结果

四、优缺点分析
优点:
- 合并排序算法具有稳定性,相同元素的相对顺序不会改变。
- 在平均情况下,合并排序的时间复杂度为O(nlogn),较低的时间复杂度保证了其高效性。
- 可以处理大规模数据的排序,适用于各种数据类型。
缺点:
- 合并排序算法需要额外的空间来存储中间结果,空间复杂度为O(n)。
- 对于小规模数据,合并排序的性能可能略低于其他简单的排序算法,由于递归调用的开销。
结论:
合并排序算法通过巧妙地利用分治策略和递归思想,实现了高效、稳定的排序功能。它在实际应用中被广泛使用,并且适用于各种数据类型和规模。然而,在面对特别大的数据集时,需要考虑额外的空间开销。了解合并排序的原理和实现方式,对于深入理解分治策略以及扩展排序算法的知识面都是非常有益的。
相关文章:

算法笔记【8】-合并排序算法
文章目录 一、前言二、合并排序算法基本原理三、实现步骤四、优缺点分析 一、前言 合并排序算法通过采用分治策略和递归思想,实现了高效、稳定的排序功能。本文将深入探讨合并排序算法的原理、实现步骤,并讨论其优缺点。 二、合并排序算法基本原理 合…...

蓝桥杯每日一题2023.10.30
题目描述 日志统计 - 蓝桥云课 (lanqiao.cn) 题目分析 本题可以使用双指针来维护时间段的区间,在维护的时间段内确定是否为热帖 #include<bits/stdc.h> using namespace std; typedef long long ll; const int N 2e5 10; struct node {int t, id; }tiee…...

macOS M1安装wxPython报错‘tiff.h‘ file not found的解决方法
macOS12.6.6 M1安装wxPython失败: 报错如下: imagtiff.cpp:37:14: fatal error: tiff.h file not found解决办法: 下载源文件重新编译(很快,5分钟全部搞定),分三步走: 第一步&…...
多路转接之epoll
本篇博客介绍: 多路转接之epoll 多路转接之epoll 初识epollepoll相关系统调用epoll的工作原理epoll服务器编写成员变量构造函数 循环函数HandlerEvent函数epoll的优缺点 我们学习epoll分为四部分 快速理解部分概念 快速的看一下部分接口讲解epoll的工作原理手写epo…...

删除排序链表中的重复节点II(C++解法)
题目 给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表 。 示例 1: 输入:head [1,2,3,3,4,4,5] 输出:[1,2,5]示例 2: 输入:head [1…...
uniapp自定义tab切换css样式、uni-forms中input下拉等标签字体、过宽、溢出样式一系列调整(附加实战举例)
一、uniapp自定义tab切换css样式 <view class="tabs-container"><view class="tabs-list">...

windows server 2016-IIS静态服务器-设置详细过程
文章目录 1.打开仪表盘新建角色2.iis功能模块3.启动服务器4.优点 1.打开仪表盘新建角色 2.iis功能模块 能选上的尽量选上,除非知道自己用不上。 然后确认,下一步,安装。 3.启动服务器 搜索IIS,启动IIS管理器。 启动网站。 右…...
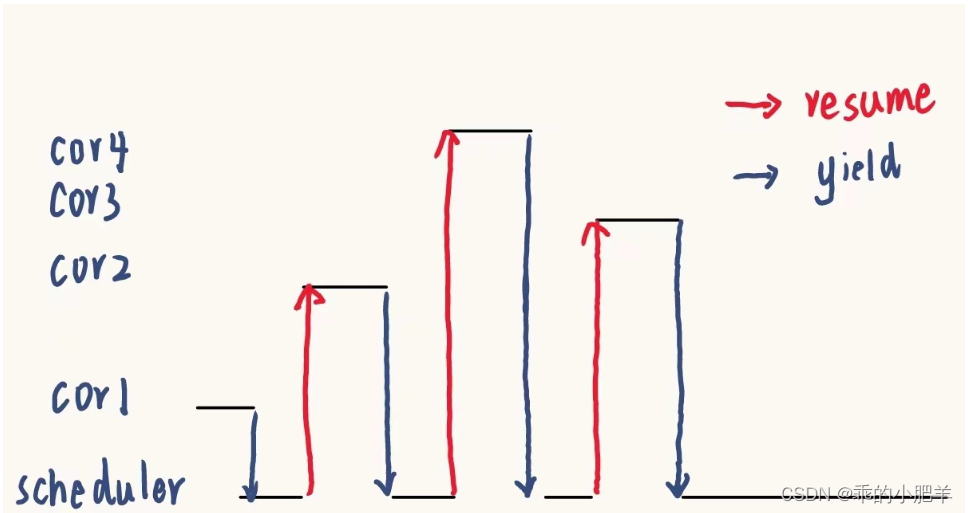
不一样的编程方式 —— 协程(设计原理与汇编实现)
主要通过以下9个方面来了解协程的原理: 目录 1、为什么使用协程 1.3、协程的适用场景 2、协程的原语操作 3、协程的切换 3.1、汇编实现 4.协程的运行流程 5.协程的结构体定义(我们其实可以参照线程或者进程的状态来设计) 5.1、多状态集合设计 6.协程的调度…...

Thinkphp6项目在虚拟机无法指向pulic的目录访问的方法
以阿里云虚拟主机为例,服务器环境为 LAMP,Apache2.4 php7.2 mysql5.7 1.根目录新建 index.php 文件,将以下内容放入文件中 <?php include ./public/index.php;2.将 public 目录下的 admin.php、backend 文件夹、static 文件夹、tinymc…...

数据结构(超详细讲解!!)第十八节 串(堆串)
1.定义 假设以一维数组heap [MAXSIZE] 表示可供字符串进行动态分配的存储空间,并设 int start 指向heap 中未分配区域的开始地址(初始化时start 0) 。在程序执行过程中,当生成一个新串时,就从start指示的位置起&#…...
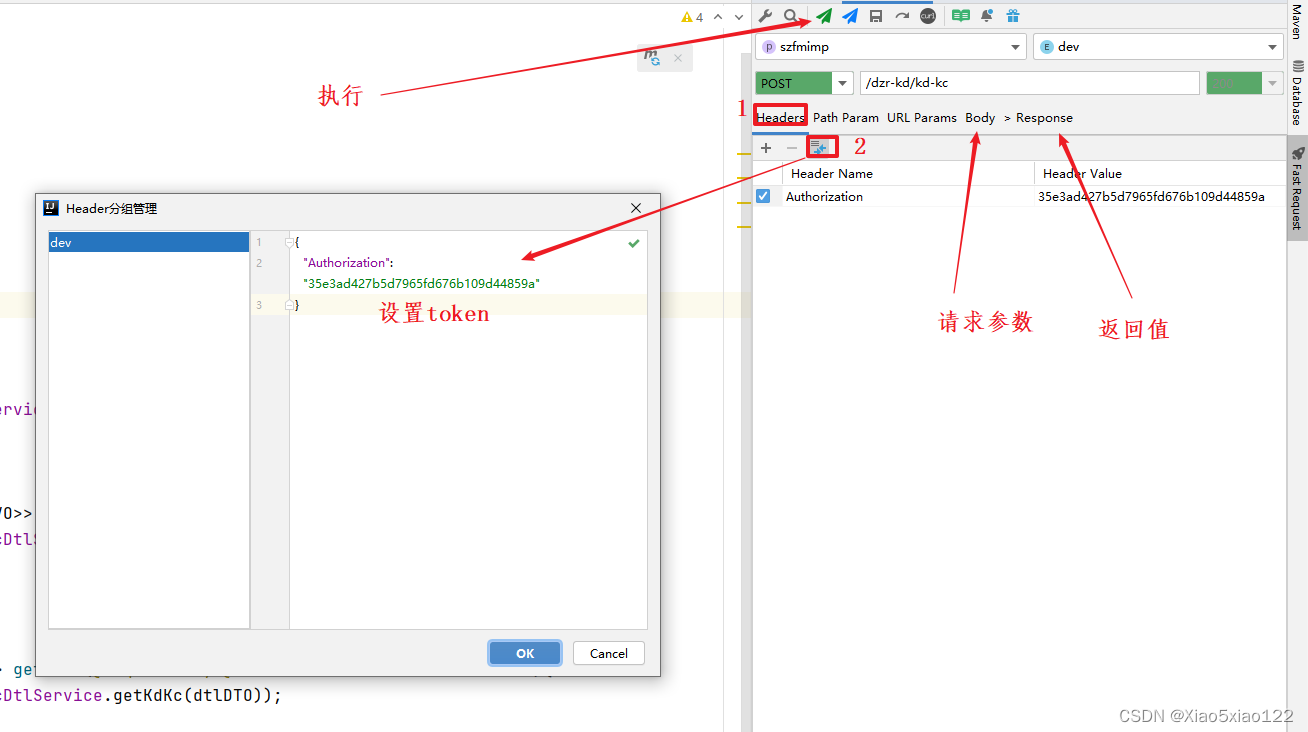
idea集成测试插件替代postman
idea集成测试插件替代postman 兄弟萌,你再测试接口是否无bug是否流畅的时候是否还在使用“postman”来回切换进行测试呢? 页面切换进行测试,有没有感觉很麻烦呢? 打开postman,输入接口地址,有没有感觉很麻烦…...

clusterprolifer go kegg msigdbr 富集分析应该使用哪个数据集,GO?KEGG?Hallmark?
关注微信:生信小博士 5 Overview of enrichment analysis Chapter 5 Overview of enrichment analysis | Biomedical Knowledge Mining using GOSemSim and clusterProfiler 5.1.2 Gene Ontology (GO) Gene Ontology defines concepts/classes used to describ…...

Linux学习笔记1-入门
前言:之前的基于单片机的闭环控制步进电机项目其实已经完成了,但很多时间都花在调试和生产上,实在没时间去做总结笔记,现在又开始做新项目了,从单片机到了Linux,想用这个平台来督促自己继续学习,…...

怎样更有效的运营Etsy店铺?
大家都知道,Etsy作为一个重要的电商平台,给很多人提供了不少机会。但是如何取得etsy店铺运营的成功呢?第一步就是选好辅助工具。 什么是指纹浏览器? VMLogin指纹浏览器(www.vmlogin.com.cn) 是一种工具,通过伪装用户…...

Vue 项目中如何使用Bootstrap5(简单易懂)
Vue 项目中如何使用Bootstrap5(简单易懂) 安装在 src/main.js 文件下引入包在vue文件中使用 Bootstrap官网(中文):https://www.bootcss.com/ Bootstrap5文档:https://v5.bootcss.com/docs/getting-started/…...

k8s 资源预留
KUBERNETES资源管理之–资源预留 Kubernetes 的节点可以按照 Capacity 调度。node节点本身除了运行不少驱动 OS 和 Kubernetes 的系统守护进程,默认情况下 pod 能够使用节点全部可用容量, 除非为这些系统守护进程留出资源,否则它们将与 pod 争…...
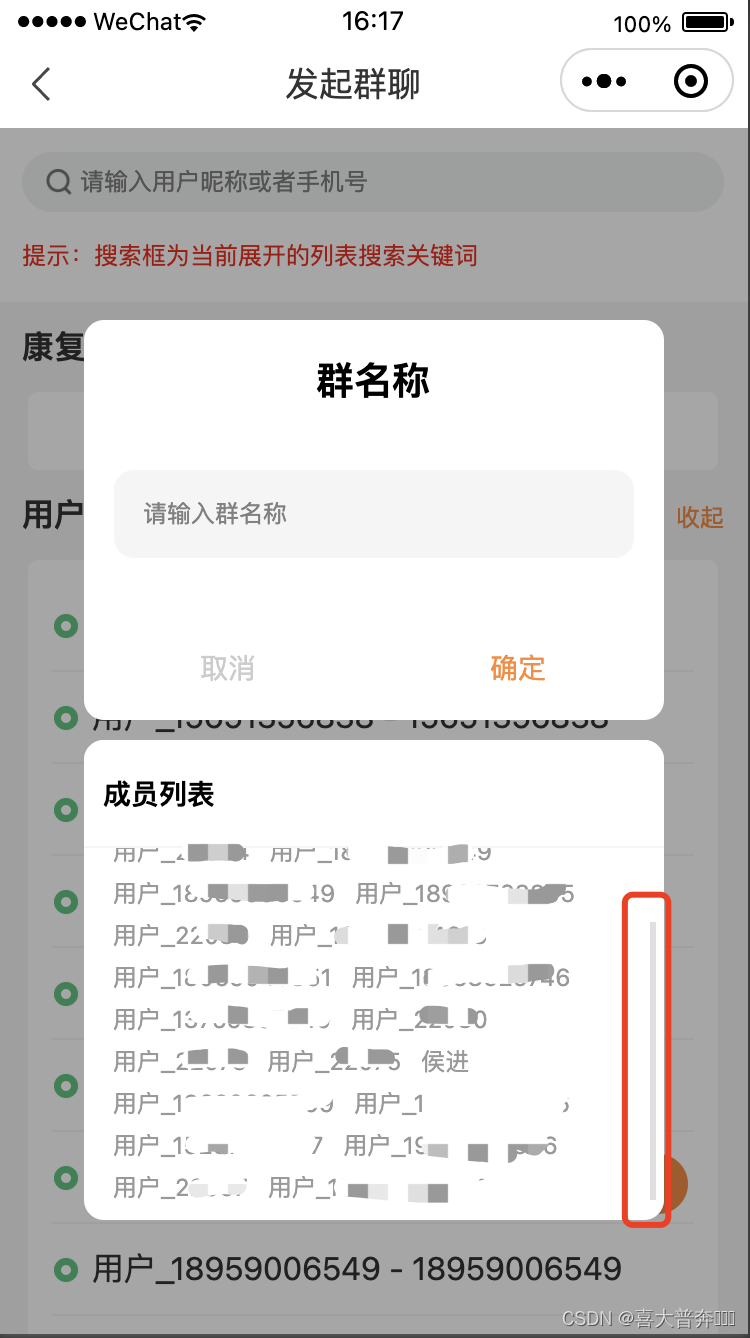
微信小程序自定义弹窗阻止滑动冒泡catchtouchmove之后弹窗内部内容无法滑动
自定义弹窗 如图所示: 自定义弹窗内部有带滚动条的盒子区域 问题: 在盒子上滑动,页面如果超出一屏的话,也会跟着一起上下滚动 解决方案:给自定义弹窗 添加 catchtouchmove 事件,阻止冒泡即可 网上不少…...

Linux 命令速查
Network ping ping -c 3 -i 0.01 127.0.0.1 # -c 指定次数 # -i 指定时间间隔 日志 一般存放位置: /var/log,包含:系统连接日志 进程统计 错误日志 常见日志文件说明 日志功能access-logweb服务访问日志acct/pacct用户命令btmp记录失…...

第22期 | GPTSecurity周报
GPTSecurity是一个涵盖了前沿学术研究和实践经验分享的社区,集成了生成预训练 Transformer(GPT)、人工智能生成内容(AIGC)以及大型语言模型(LLM)等安全领域应用的知识。在这里,您可以…...

JavaScript前端 console 控制台详细解析与代码实例
JavaScript Console(控制台)是一个重要的工具,可以用于调试和测试 JavaScript 代码。在浏览器中,你可以使用控制台来查看 JavaScript 输出、测试代码、调试错误等。在本文中,我们将详细介绍控制台的常用功能和代码实例…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
