【考研数学】概率论与数理统计 —— 第七章 | 参数估计(2,参数估计量的评价、正态总体的区间估计)
文章目录
- 一、参数估计量的评价标准
- 1.1 无偏性
- 1.2 有效性
- 1.3 一致性
- 二、一个正态总体参数的双侧区间估计
- 三、一个正态总体的单侧置信区间
- 四、两个正态总体的双侧置信区间
- 写在最后
一、参数估计量的评价标准
1.1 无偏性
设 X X X 为总体, ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots ,X_n) (X1,X2,⋯,Xn) 为来自总体 X X X 的简单随机样本, θ \theta θ 为未知参数,设 θ ^ = φ ( X 1 , X 2 , ⋯ , X n ) \widehat{\theta}=\varphi(X_1,X_2,\cdots,X_n) θ =φ(X1,X2,⋯,Xn) 为参数 θ \theta θ 的一个点估计量,若 E ( θ ^ ) = θ E(\widehat{\theta})=\theta E(θ )=θ ,称 θ ^ \widehat{\theta} θ 为参数 θ \theta θ 的无偏估计量。
【例】 设总体 X X X 的密度函数为 f ( x ) = { 2 x / θ 2 0 < x < θ 0 e l s e f(x)=\begin{cases} 2x/\theta^2 & 0<x<\theta \\ 0 &else\end{cases} f(x)={2x/θ200<x<θelse ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots,X_n) (X1,X2,⋯,Xn) 为来自总体 X X X 的简单随机样本。
(1)求参数 θ \theta θ 的矩估计量;(2)求参数 θ \theta θ 的最大似然估计量;(3)矩估计量是否为无偏估计。
解: (1) E ( X ) = ∫ − ∞ ∞ x f ( x ) d x = 2 θ / 3 E(X)=\int_{-\infty}^\infty xf(x)dx=2\theta/3 E(X)=∫−∞∞xf(x)dx=2θ/3 ,令 2 θ / 3 = X ‾ 2\theta/3=\overline{X} 2θ/3=X ,则可得矩估计量 θ ^ = 3 X ‾ 2 . \widehat{\theta}=\frac{3\overline{X}}{2}. θ =23X. (2)构造似然函数 L ( θ ) = f ( x 1 ) f ( x 2 ) ⋯ f ( x n ) = 2 n θ 2 n x 1 x 2 ⋯ x n ( 0 < x i < θ , i = 1 , 2 , ⋯ , n ) . d ln L d θ = − 2 n θ < 0. L(\theta)=f(x_1)f(x_2)\cdots f(x_n)=\frac{2^n}{\theta^{2n}}x_1x_2\cdots x_n(0<x_i<\theta,i=1,2,\cdots,n).\\ \frac{d\ln L}{d\theta}=-\frac{2n}{\theta}<0. L(θ)=f(x1)f(x2)⋯f(xn)=θ2n2nx1x2⋯xn(0<xi<θ,i=1,2,⋯,n).dθdlnL=−θ2n<0. 可知 L ( θ ) L(\theta) L(θ) 是 θ \theta θ 的减函数,因此最大似然估计量 θ ^ = max { X 1 , X 2 , ⋯ , X n } \widehat{\theta}=\max\{X_1,X_2,\cdots,X_n\} θ =max{X1,X2,⋯,Xn} 。
(3) E ( θ ^ ) = 3 / 2 ⋅ E ( X ‾ ) = 3 / 2 ⋅ 2 θ / 3 = θ E(\widehat{\theta})=3/2\cdot E(\overline{X})=3/2\cdot2\theta/3=\theta E(θ )=3/2⋅E(X)=3/2⋅2θ/3=θ ,故是无偏估计量。
1.2 有效性
设 X X X 为总体, ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots ,X_n) (X1,X2,⋯,Xn) 为来自总体 X X X 的简单随机样本, θ \theta θ 为未知参数,设 θ ^ 1 , θ ^ 2 \widehat{\theta}_1,\widehat{\theta}_2 θ 1,θ 2 都是参数 θ \theta θ 的无偏估计量,若 D ( θ ^ 1 ) < D ( θ ^ 2 ) D(\widehat{\theta}_1)<D(\widehat{\theta}_2) D(θ 1)<D(θ 2) ,称 θ ^ 1 \widehat{\theta}_1 θ 1 为更有效的参数估计量。
1.3 一致性
设 X X X 为总体, ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots ,X_n) (X1,X2,⋯,Xn) 为来自总体 X X X 的简单随机样本, θ \theta θ 为未知参数,设 θ ^ = φ ( X 1 , X 2 , ⋯ , X n ) \widehat{\theta}=\varphi(X_1,X_2,\cdots,X_n) θ =φ(X1,X2,⋯,Xn) 为参数 θ \theta θ 的一个估计量,若对任意 ϵ > 0 \epsilon>0 ϵ>0 ,有 lim n → ∞ P { ∣ θ ^ − θ ∣ < ϵ } = 1 \lim_{n\to\infty}P\{|\widehat{\theta}-\theta|<\epsilon\}=1 n→∞limP{∣θ −θ∣<ϵ}=1 称 θ ^ \widehat{\theta} θ 作为 θ \theta θ 的估计量具有一致性(或相合性)。
二、一个正态总体参数的双侧区间估计
前面我们所学的两种方法为点估计法,即只能得到一个值,但实际上我们并非需要那么精确,况且点估计出来也不一定好,因此我们最好是估计一个区间范围。
2.1 对参数 μ \mu μ 的双侧区间估计
设 X ∼ N ( μ , σ 2 ) X \sim N(\mu,\sigma^2) X∼N(μ,σ2) 为总体, ( X 1 , X 2 , ⋯ , X n ) (X_1,X_2,\cdots ,X_n) (X1,X2,⋯,Xn) 为来自总体 X X X 的简单随机样本, 0 < α < 1 0<\alpha<1 0<α<1 ,求参数的置信度为 1 − α 1-\alpha 1−α 的双侧置信区间。
1. 参数 σ 2 \sigma^2 σ2 已知
对 X ‾ \overline{X} X 标准化为标准正态分布,令其在 − z α 2 -z_{\alpha\over 2} −z2α 和 z α 2 z_{\alpha\over 2} z2α 内的概率为 1 − α 1-\alpha 1−α,可求出置信区间为 ( X ‾ − σ n z α 2 , X ‾ + σ n z α 2 ) \bigg(\overline{X}-\frac{\sigma}{\sqrt{n}}z_{\alpha\over2},\overline{X}+\frac{\sigma}{\sqrt{n}}z_{\alpha\over2}\bigg) (X−nσz2α,X+nσz2α) 2. 参数 σ 2 \sigma^2 σ2 未知
则利用 t t t 分布,即取 X ‾ − μ S n ∼ t ( n − 1 ) \frac{\overline{X}-\mu}{\frac{S}{\sqrt{n}}}\sim t(n-1) nSX−μ∼t(n−1) 令其在 ( − t α 2 ( n − 1 ) , t α 2 ( n − 1 ) ) (-t_{\frac{\alpha}{2}}(n-1),t_{\frac{\alpha}{2}}(n-1)) (−t2α(n−1),t2α(n−1)) 的概率为 1 − α 1-\alpha 1−α ,可计算出置信区间为 ( X ‾ − S n t α 2 ( n − 1 ) , X ‾ + S n t α 2 ( n − 1 ) ) \bigg(\overline{X}-\frac{S}{\sqrt{n}}t_{\alpha\over2}(n-1),\overline{X}+\frac{S}{\sqrt{n}}t_{\alpha\over2}(n-1)\bigg) (X−nSt2α(n−1),X+nSt2α(n−1)) 此外还有对 σ 2 \sigma^2 σ2 的区间估计,汇总成下表:

三、一个正态总体的单侧置信区间
其实单侧也就是双侧的区间取一端,如估计 μ \mu μ 且 σ 2 \sigma^2 σ2 已知,单侧置信区间为: ( X ‾ − σ n z α 2 , + ∞ ) , ( − ∞ , X ‾ + σ n z α 2 ) \bigg(\overline{X}-\frac{\sigma}{\sqrt{n}}z_{\alpha\over2},+\infty\bigg),\bigg(-\infty,\overline{X}+\frac{\sigma}{\sqrt{n}}z_{\alpha\over2}\bigg) (X−nσz2α,+∞),(−∞,X+nσz2α) 其余以此类推。
四、两个正态总体的双侧置信区间
汇总成表:

其中 S w = ( m − 1 ) S 1 2 + ( n − 1 ) S 2 2 m + n − 2 S_w=\frac{(m-1)S_1^2+(n-1)S_2^2}{m+n-2} Sw=m+n−2(m−1)S12+(n−1)S22
写在最后
看了下大纲,对区间估计的概念和一个、两个正态总体的置信区间公式作了理解要求,后期抽时间记忆记忆。
相关文章:

【考研数学】概率论与数理统计 —— 第七章 | 参数估计(2,参数估计量的评价、正态总体的区间估计)
文章目录 一、参数估计量的评价标准1.1 无偏性1.2 有效性1.3 一致性 二、一个正态总体参数的双侧区间估计2.1 对参数 μ \mu μ 的双侧区间估计 三、一个正态总体的单侧置信区间四、两个正态总体的双侧置信区间写在最后 一、参数估计量的评价标准 1.1 无偏性 设 X X X 为总…...
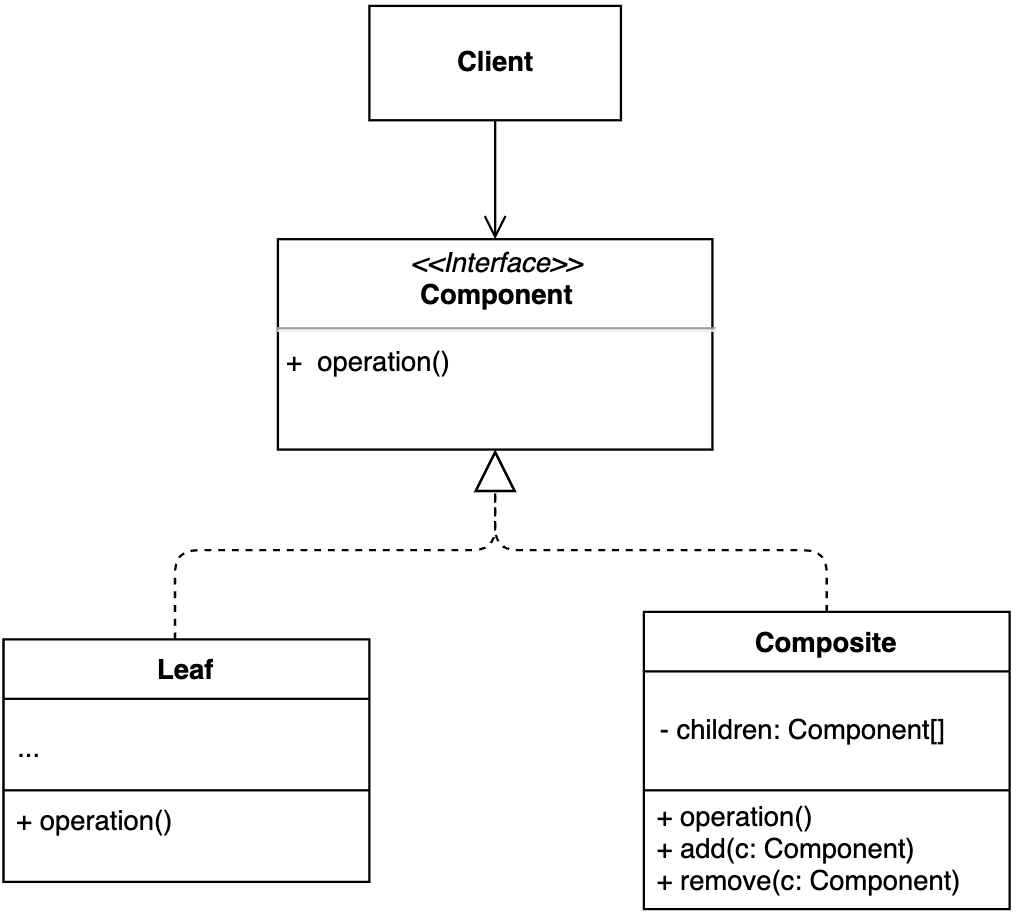
【设计模式】第10节:结构型模式之“组合模式”
一、简介 组合模式:将一组对象组织成树形结构,将单个对象和组合对象都看做树中的节点,以统一处理逻辑,并且它利用树形结构的特点,递归地处理每个子树,依次简化代码实现。使用组合模式的前提在于࿰…...

改进YOLOv3!IA-YOLO:恶劣天气下的目标检测
恶劣天气条件下从低质量图像中定位目标还是极具挑战性的任务。现有的方法要么难以平衡图像增强和目标检测任务,要么往往忽略有利于检测的潜在信息。本文提出了一种新的图像自适应YOLO (IA-YOLO)框架,可以对每张图像进行自适应增强,以提高检测…...

Vue路由跳转的几种方式
1.this. $router.push( ) 跳转到指定的URL,在history栈中添加一个记录,点击后退会返回上一个页面。 1. 不带参数// 字符串this.$router.push(/home)this.$router.push(/home/first)// 对象this.$router.push({path:/home})this.$router.push({ path: /…...

TiDB x 汉口银行丨分布式数据库应用实践
汉口银行是一家城市商业银行,近年来专注科技金融、民生金融等领域。在数据库国产化改造中,汉口银行引入了 TiDB 数据库,并将其应用在重要业务系统:头寸系统中,实现了一栈式的数据服务,同时满足了高并发、低…...

uci机器学习数据库简介
UCI(University of California, Irvine)机器学习数据库是经过精心整理的、用于研究和开发机器学习算法的数据集合。UCI机器学习数据库是一个公开的、广泛使用的数据集合,它由加州大学欧文分校的计算机科学系维护。该数据库中包含了许多数据集…...
多人协作使用git如何解决冲突?
什么情况会产生冲突 git merge XXX(合并分支时的冲突): 当你尝试将一个分支的更改合并到另一个分支时,如果两个分支都修改了相同的文件的相同部分,Git 将无法自动解决冲突,因此会发生冲突。你需要手动解决这些冲突,然后…...

基于【逻辑回归】的评分卡模型金融借贷风控项目实战
背景知识: 在银行借贷过程中,评分卡是一种以分数形式来衡量一个客户的信用风险大小的手段。今天我们来复现一个评分A卡的模型。完整的模型开发所需流程包括:获取数据,数据清洗和特征工程,模型开发,…...

企业拉美跨境出海面对时延情况怎么办?
随着全球化不断发展,中国企业也不断向海外拓展业务,开拓市场,增加收入来源,扩大自身品牌影响力。然而出海企业面临不同以往的困难和挑战,在其中不可避免面临的跨境网络时延问题,如何选择区域进行部署企业业…...

【vector题解】只出现一次的数字 | 电话号码的数字组合
只出现一次的数字 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。 你必须设计并…...
VS2022 开发方式
使用 C# 在VS 2022 上开发时,发现有多种项目类型可以创建。这些类型放一起容易搞混,于是记录一下各种类型的区别。 这里主要介绍windows控制台程序、MFC程序、WPF程序、WinForm程序的特点。 创建哪种应用? 创建控制台应用 Windows控制台程序…...

【Python语言速回顾】——数据可视化基础
目录 引入 一、Matplotlib模块(常用) 1、绘图流程&常用图 编辑 2、绘制子图&添加标注 编辑 3、面向对象画图 4、Pylab模块应用 二、Seaborn模块(常用) 1、常用图 2、代码示例 编辑 编辑 编辑 …...
java实现pdf文件添加水印,下载到浏览器
java实现pdf文件添加水印,下载到浏览器 添加itextpdf依赖 <dependency><groupId>com.itextpdf</groupId><artifactId>itextpdf</artifactId><version>5.5.8</version> </dependency>文件下载到浏览器和指定路径 …...
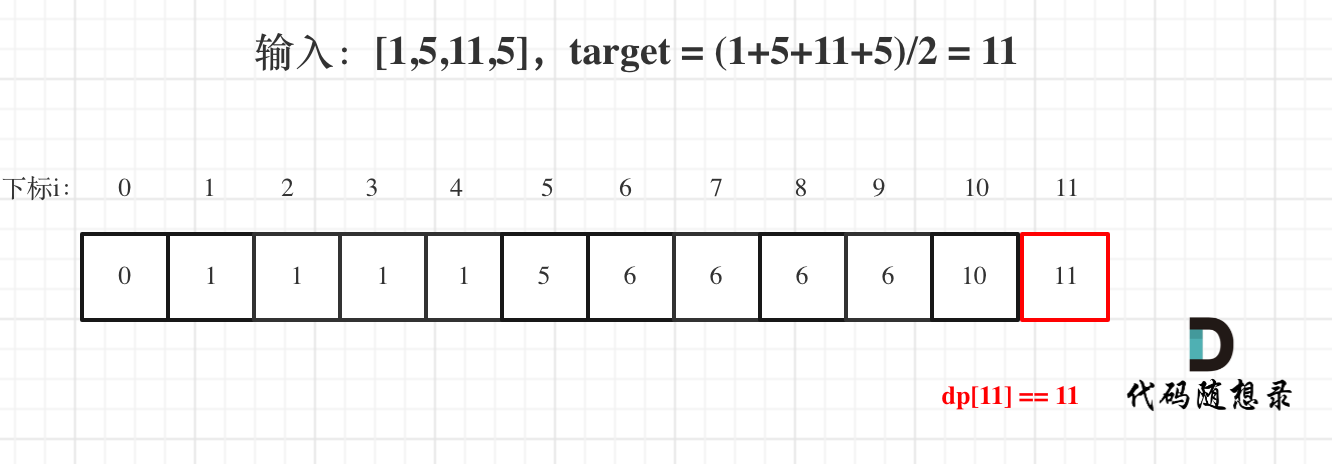
代码随想录算法训练营第四十一天丨 动态规划part04
01背包理论基础 见连接:代码随想录 416. 分割等和子集 思路 01背包问题 背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解…...

PyCharm免费安装和新手使用教程
简介 PyCharm是一款由JetBrains公司开发的Python集成开发环境(IDE)。它提供了一系列强大的功能,包括自动代码完成、语法高亮、自动缩进、代码重构、调试器、测试工具、版本控制工具等,使开发者可以更加高效地开发Python应用程序。…...

使用Python的Scikit-Learn进行决策树建模和可视化:以隐形眼镜数据集为例
决策树是一种强大的机器学习算法,它在数据挖掘和模式识别中被广泛应用。决策树模型可以帮助我们理解数据中的模式和规则,并做出预测。在本文中,我们将介绍如何使用Python的Scikit-Learn库构建决策树模型,并使用Graphviz进行可视化…...

开源软件:释放创新的力量,改变数字世界的游戏规则
在充满活力的技术领域,创新是至高无上的,有一种方法已获得显著的吸引力——开源软件。开源软件凭借其透明、协作和无限可能性的精神,彻底改变了我们开发、共享和定制应用程序的方式。从操作系统到数据分析工具,其影响跨越了多个领…...
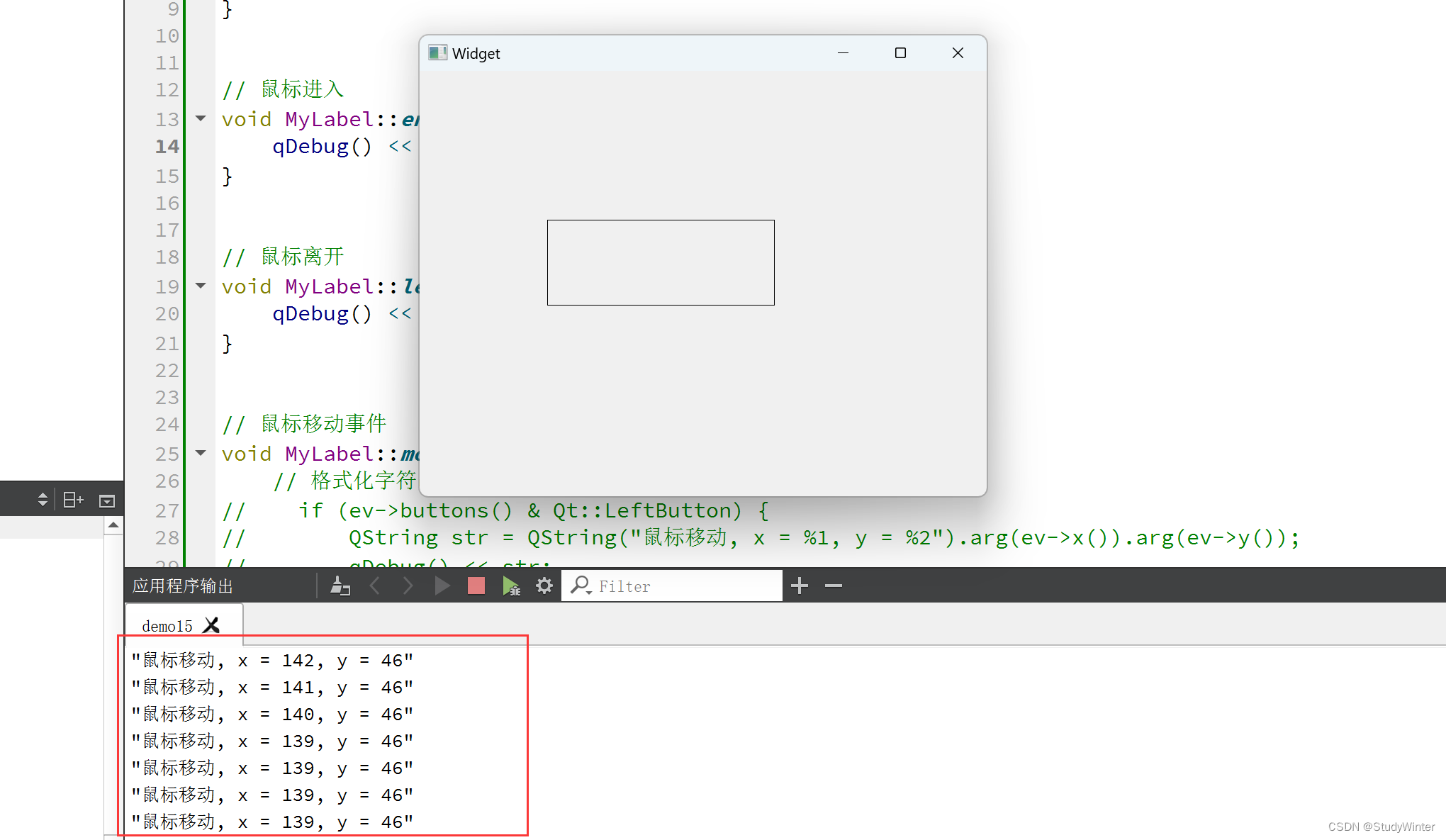
【QT】鼠标常用事件
新建项目 加标签控件 当鼠标进去,显示【鼠标进入】,离开时显示【鼠标离开】 将QLable提升成自己的控件,然后再去捕获 添加文件 改继承的类名 提升类 同一个父类,可以提升 效果 现在代码就和Qlabel对应起来了。 在.h中声明&…...
--mlx90640 - 红外测温(MLX90640))
LuatOS-SOC接口文档(air780E)--mlx90640 - 红外测温(MLX90640)
常量# 常量 类型 解释 mlx90640.FPS1HZ number FPS1HZ mlx90640.FPS2HZ number FPS2HZ mlx90640.FPS4HZ number FPS4HZ mlx90640.FPS8HZ number FPS8HZ mlx90640.FPS16HZ number FPS16HZ mlx90640.FPS32HZ number FPS32HZ mlx90640.FPS64HZ number FPS6…...

java连接本地数据库可以简写为///
java连接数据库配置文件写为: server:port: 8091 spring:application:name: user-managerdatasource:driver-class-name: com.mysql.cj.jdbc.Driverurl: jdbc:mysql://localhost:3306/user?serverTimezoneAsia/Shanghai&characterEncodingutf-8username: root…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
