ccc-台大林轩田机器学习基石-hw1
文章目录
- Question1-14
- Question15-PLA
- Question16-PLA平均迭代次数
- Question17-不同迭代系数的PLA
- Question18-Pocket_PLA
- Question19-PLA的错误率
- Question20-修改Pocket_PLA迭代次数
Question1-14

对于有明确公式和定义的不需要使用到ml

智能系统在与环境的连续互动中学习最优行为策略的机器学习问题,学习最优的序贯决策

无标签分类
从标注数据 学习预测模型

主动地提出一些标注请求,将一些经过筛选的数据提交给专家进行标注

- 解题关键是计算N+1到N+L上的偶数个数
- 0到N的偶数个数是⌊N⌋2\frac{ ⌊N⌋}{2}2⌊N⌋
- 问题转化成(0到N+L的偶数个数-0到N的偶数个数)

generate了D,但是N+1到N+L上L个点没有generate。每个点都有{被generate,没被generate}两种可能,所以是2L2^L2L

由“无免费午餐定理”可知,任何算法在没有噪声时对于未知样本期望相等

P(5orange&5else)=C105210P(5orange\&5else)=\frac{C_{10}^5}{2^{10}}P(5orange&5else)=210C105
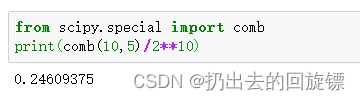
from scipy.special import comb
print(comb(10,5)/2**10)

P(9orange&1else)=C1090.99×0.1P(9orange\&1else)=\frac{C_{10}^9}{0.9^{9}\times0.1}P(9orange&1else)=0.99×0.1C109
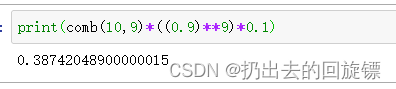
print(comb(10,9)*((0.9)**9)*0.1)

- 分v=0.1和0时讨论
P=C101(910)1(110)9+C100(110)10P=C_{10}^1{(\frac 9{10})^{1}{(\frac 1 {10})}^{9} }+C_{10}^0{{(\frac 1 {10})}^{10}}P=C101(109)1(101)9+C100(101)10


Hoeffding:P[∣μ−v∣>ϵ]≤2e−2ϵ2NP[v≤0.1]=P[0.9−v≥0.8]=P[μ−v≥0.8]≤P[∣μ−v∣≥0.8]≤2e−2×0.82×10≈5.5215451440744015×10−6Hoeffding:\mathbb P[| \mu-v|>\epsilon]\le 2e^{-2\epsilon ^2N}\\ \begin{aligned} \mathbb P[v\le 0.1] &=P[0.9-v\ge 0.8]\\ &=P[\mu-v\ge 0.8]\\ &\le P[|\mu-v|\ge 0.8]\\ &\le 2e^{-2\times 0.8^2\times 10}\\ &\approx5.5215451440744015\times 10^{-6} \end{aligned}Hoeffding:P[∣μ−v∣>ϵ]≤2e−2ϵ2NP[v≤0.1]=P[0.9−v≥0.8]=P[μ−v≥0.8]≤P[∣μ−v∣≥0.8]≤2e−2×0.82×10≈5.5215451440744015×10−6

- A:奇数绿,偶数橙
- B:奇数橙,偶数绿
- C:1-3橙,4-6绿
- D:1-3绿,4-6橙
5个橙1,只可能是BC中,所以132=8256\frac{1}{32}=\frac{8}{256}321=2568

- 1全橙:BC
- 2全橙:AC
- 3全橙:BC
- 4全橙:AD
- 5全橙:BD
- 6全橙:AD
- 全A,B,C,D被重复算了一遍,要减去4
P=4×25−445=31256P=\frac{4\times2^5-4}{4^5}=\frac {31}{256}P=454×25−4=25631

Question15-PLA

data链接

代码部分:
utils函数:
import numpy as np
#判别函数,判断所有数据是否分类完成
def Judge(X, y, w):n = X.shape[0]num = np.sum(X.dot(w) * y > 0)return num == ndef PLA(X, y, eta=1, max_step=np.inf):# 获取维度n, d = X.shape# 初始化w = np.zeros(d)# 迭代次数t = 0# 元素的下标i = 0# 错误的下标last = 0while not (Judge(X, y, w)) :if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]# 更新错误last = i# 移动到下一个元素,如果达到n,则重置为0i += 1if i == n:i = 0return t, last, w
主函数:
import numpy as np
import utils as util#读取数据
data = np.genfromtxt("hw1_15_train.dat")
#获取维度
n, d = data.shape
#分离X
X = data[:, :-1]
#添加偏置项1
X = np.c_[np.ones(n), X]
#分离y
y = data[:, -1]
print(util.PLA(X, y))
运行结果:

Question16-PLA平均迭代次数

代码部分:
utils函数:
import numpy as np
import matplotlib.pyplot as pltdef Judge(X, y, w):n = X.shape[0]num = np.sum(X.dot(w) * y > 0)return num == ndef PLA(X, y, eta=1):n, d = X.shapew = np.zeros(d)t = 0i = 0last = 0while not (Judge(X, y, w)):if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]last = ii += 1if i == n:i = 0return t, last, w#运行g算法n次并返回平均的迭代次数
def average_of_n(g, X, y, n, eta=1):result = []data = np.c_[X, y]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]result.append(g(X, y, eta=eta)[0])plt.hist(result)plt.xlabel("迭代次数")plt.title("平均运行次数为" + str(np.mean(result)))plt.show()
主函数:
import numpy as np
import utils as util
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False #显示负号data = np.genfromtxt("hw1_15_train.dat")
#获取维度
n, d = data.shape
#分离X
X = data[:, :-1]
#添加偏置项1
X = np.c_[np.ones(n), X]
#分离y
y = data[:, -1]
util.average_of_n(util.PLA, X, y, 2000, 1)
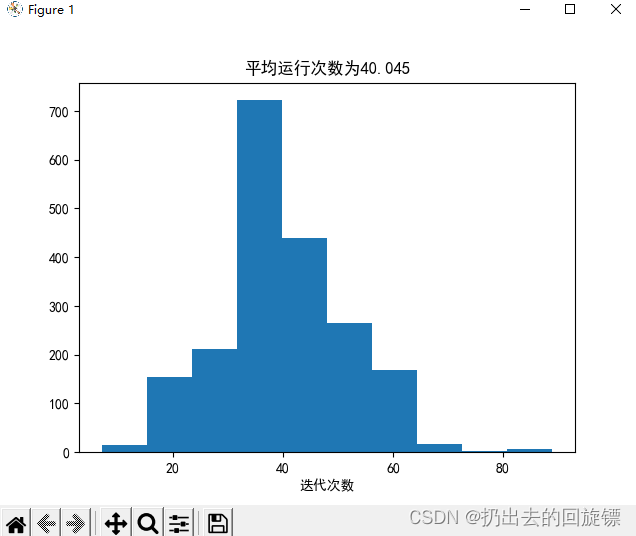
Question17-不同迭代系数的PLA
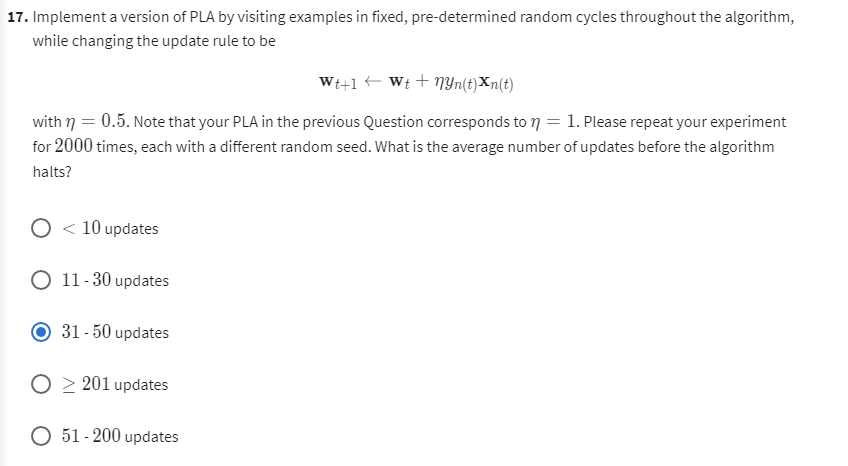
修改迭代系数即可:
util.average_of_n(util.PLA, X, y, 2000, 0.5)
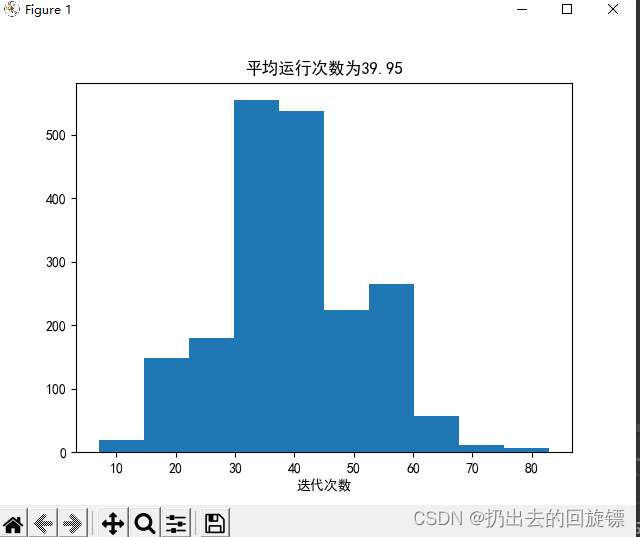
Question18-Pocket_PLA
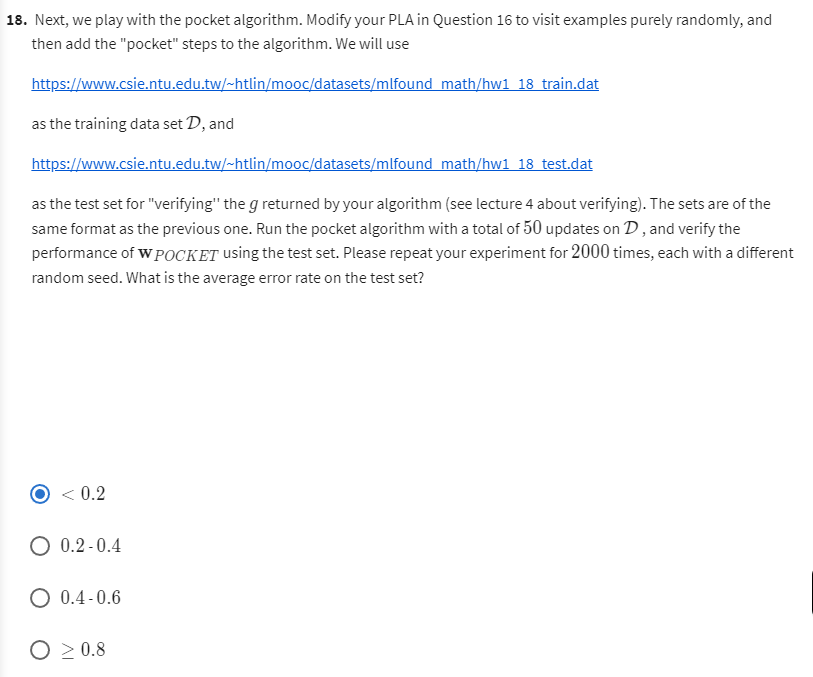
utils函数:
import matplotlib.pyplot as plt
import numpy as np
#统计错误数量
def count(X, y, w):num = np.sum(X.dot(w) * y <= 0)return np.sum(num)#预处理
def preprocess(data):# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef Pocket_PLA(X, y, eta=1, max_step=np.inf):#max_step 限制迭代次数#获得数据维度n, d = X.shape#初始化w = np.zeros(d)#记录最优向量w0 = np.zeros(d)#记录次数t = 0#记录最少错误数量error = count(X, y, w0)#记录元素的下标i = 0while (error != 0 and t < max_step):if np.sign(X[i, :].dot(w) * y[i]) <= 0:w += eta * y[i] * X[i, :]#迭代次数增加t += 1#记录当前错误error_now = count(X, y, w)if error_now < error:error = error_noww0 = np.copy(w)#移动到下一个元素i += 1#如果达到n,则重置为0if i == n:i = 0return error, w0#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.Pocket_PLA, X_train, y_train, X_test, y_test, 2000, max_step=50)
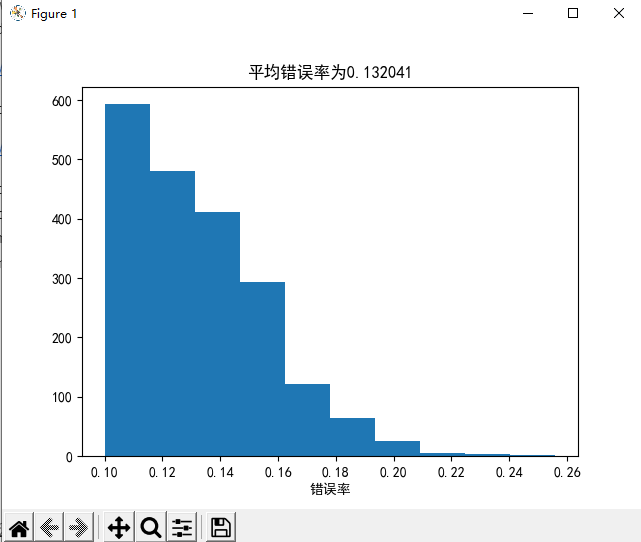
Question19-PLA的错误率

utils函数:
import matplotlib.pyplot as plt
import numpy as npdef count(X, y, w):#判断是否同号num = np.sum(X.dot(w) * y <= 0)return np.sum(num)def Judge(X, y, w):n = X.shape[0]#判断是否同号num = np.sum(X.dot(w) * y > 0)return num == ndef preprocess(data):"""数据预处理"""# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef PLA(X, y, eta=1,max_step=np.inf):n, d = X.shapew = np.zeros(d)t = 0i = 0last = 0while not (Judge(X, y, w)) and t<max_step:if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]last = ii += 1if i == n:i = 0return t, last, w#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.PLA, X_train, y_train, X_test, y_test, 2000, max_step=50)
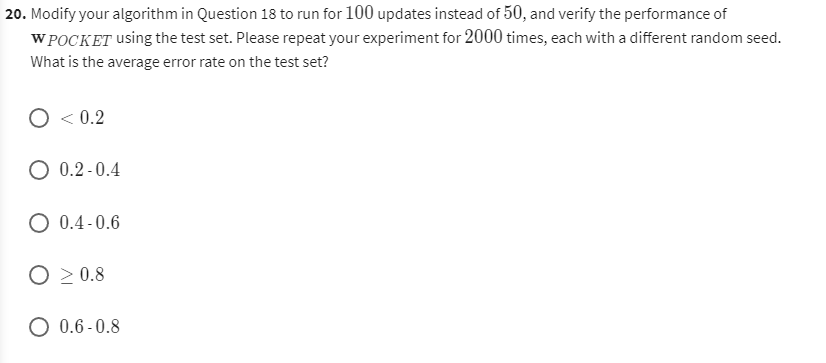
Question20-修改Pocket_PLA迭代次数
utils函数:
import matplotlib.pyplot as plt
import numpy as npdef count(X, y, w):#判断是否同号num = np.sum(X.dot(w) * y <= 0)return np.sum(num)def Judge(X, y, w):n = X.shape[0]#判断是否同号num = np.sum(X.dot(w) * y > 0)return num == ndef preprocess(data):"""数据预处理"""# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef Pocket_PLA(X, y, eta=1, max_step=np.inf):#max_step 限制迭代次数#获得数据维度n, d = X.shape#初始化w = np.zeros(d)#记录最优向量w0 = np.zeros(d)#记录次数t = 0#记录最少错误数量error = count(X, y, w0)#记录元素的下标i = 0while (error != 0 and t < max_step):if np.sign(X[i, :].dot(w) * y[i]) <= 0:w += eta * y[i] * X[i, :]#迭代次数增加t += 1#记录当前错误error_now = count(X, y, w)if error_now < error:error = error_noww0 = np.copy(w)#移动到下一个元素i += 1#如果达到n,则重置为0if i == n:i = 0return error, w0#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.Pocket_PLA, X_train, y_train, X_test, y_test, 2000, max_step=100)
相关文章:

ccc-台大林轩田机器学习基石-hw1
文章目录Question1-14Question15-PLAQuestion16-PLA平均迭代次数Question17-不同迭代系数的PLAQuestion18-Pocket_PLAQuestion19-PLA的错误率Question20-修改Pocket_PLA迭代次数Question1-14 对于有明确公式和定义的不需要使用到ml 智能系统在与环境的连续互动中学习最优行为策…...

hadoop03-MapReduce【尚硅谷】
大数据学习笔记 MapReduce 一、MapReduce概述 MapReduce是一个分布式运算程序的编程框架,是基于Hadoop的数据分析计算的核心框架。 MapReduce处理过程为两个阶段:Map和Reduce。 Map负责把一个任务分解成多个任务;Reduce负责把分解后多任务处…...

测牛学堂:软件测试python学习之异常处理
python的捕获异常 程序在运行时,如果python解释器遇到一个错误,则会停止程序的执行,并且提示一些错误信息,这就是异常。 程序停止执行并且提示错误信息,称之为抛出异常。 因为程序遇到错误会停止执行,有时…...

图神经网络--图神经网络
图神经网络 图神经网络图神经网络一、PageRank简介1.1互联网的图表示1.2PageRank算法概述1.3求解PageRank二、代码实战2.1引入库2.2加载数据,并构建图2.3计算每个节点PageRank重要度2.4用节点尺寸可视化PageRank值一、PageRank简介 PageRank是Google最早的搜索引擎…...

React useCallback如何使其性能最大化?
前言 React中最让人畅谈的就是其带来的灵活性,可以说写起来非常的舒服。但是也就是它的灵活性太强,往往让我们忽略了很多细节的地方,而就是这些细节的东西能进行优化,减小我们的性能开销。可以说刚学React和工作几年后写React的代…...
长尾关键词使用方法,通过什么方式挖掘长尾关键词?
当你在搜索引擎的搜索栏中输入有关如何使用长尾关键词的查询时,你可能希望有简单快捷的方式出现在搜索结果中,可以帮助你更好地应用seo。 不过,这里要记住一件事:SEO 策略只会为你的网站带来流量;在你的产品良好之前&a…...

【网络编程套接字(一)】
网络编程套接字(一)理解源IP地址和目的IP地址理解源MAC地址和目的MAC地址理解源端口号和目的端口号PORT VS PID认识TCP协议和UDP协议网络字节序socket编程接口socket常见APIsockaddr结构简单的UDP网络程序服务端创建套接字服务端绑定字符串IP VS 整数IP客…...
shell脚本入门
实习的时候第一个月的考核就是如何部署一个云资源,当时走的捷径(杠杠的搜索能力hhhh)找到了一个shell脚本一键部署,后来被leader问起来就如实说了,leader问有没有看懂shell脚本中的逻辑……(没有࿰…...
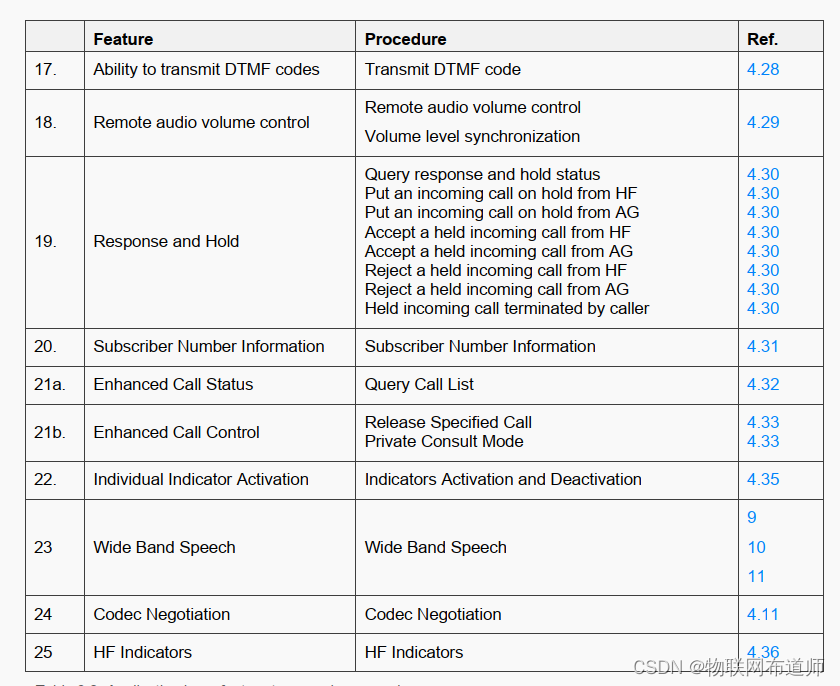
【经典蓝牙】 蓝牙HFP层协议分析
HFP 概述 HFP概念介绍 HFP(Hands-Free Profile), 是蓝牙免提协议, 可以让蓝牙设备对对端蓝牙设备的通话进行控制,例如蓝牙耳机控制手机通话的接听、 挂断、 拒接、 语音拨号等。HFP中蓝牙两端的数据交互是通过定义好的AT指令来通讯的。 &am…...
)
互联网摸鱼日报(2023-02-26)
互联网摸鱼日报(2023-02-26) InfoQ 热门话题 迁移工具 Air2phin 宣布开源,2 步迁移 Airflow 至 Dolphinscheduler 专访奇安信董国伟博士:目前开源安全的现状并不乐观,但其重要性已成各方共识 专访Brian Behlendorf&…...

关于程序员中年危机的一个真实案例
关于中年危机,网上已经有了各种各样的解读。但是,这两天一个学员跟我简单几句聊天,却触发了对于中年危机的另一种思考。如果你曾经也有点迷茫,或许你可以稍微花几分钟看下这个故事。 一、无奈的故事 39岁还出来面试&#x…...
【fly-iot飞凡物联】(2):如何从0打造自己的物联网平台,使用开源的技术栈搭建一个高性能的物联网平台,目前在设计阶段。
目录前言1,fly-iot 飞凡物联2,mqtt-broker 服务3, 管理后台产品/设备设计4,数据存储目前使用mysql,消息存储到influxdb中5,规则引擎使用 ekuiper6, 总结和其他的想法前言 本文的原文连接是: https://blog.csdn.net/freewebsys/article/detail…...
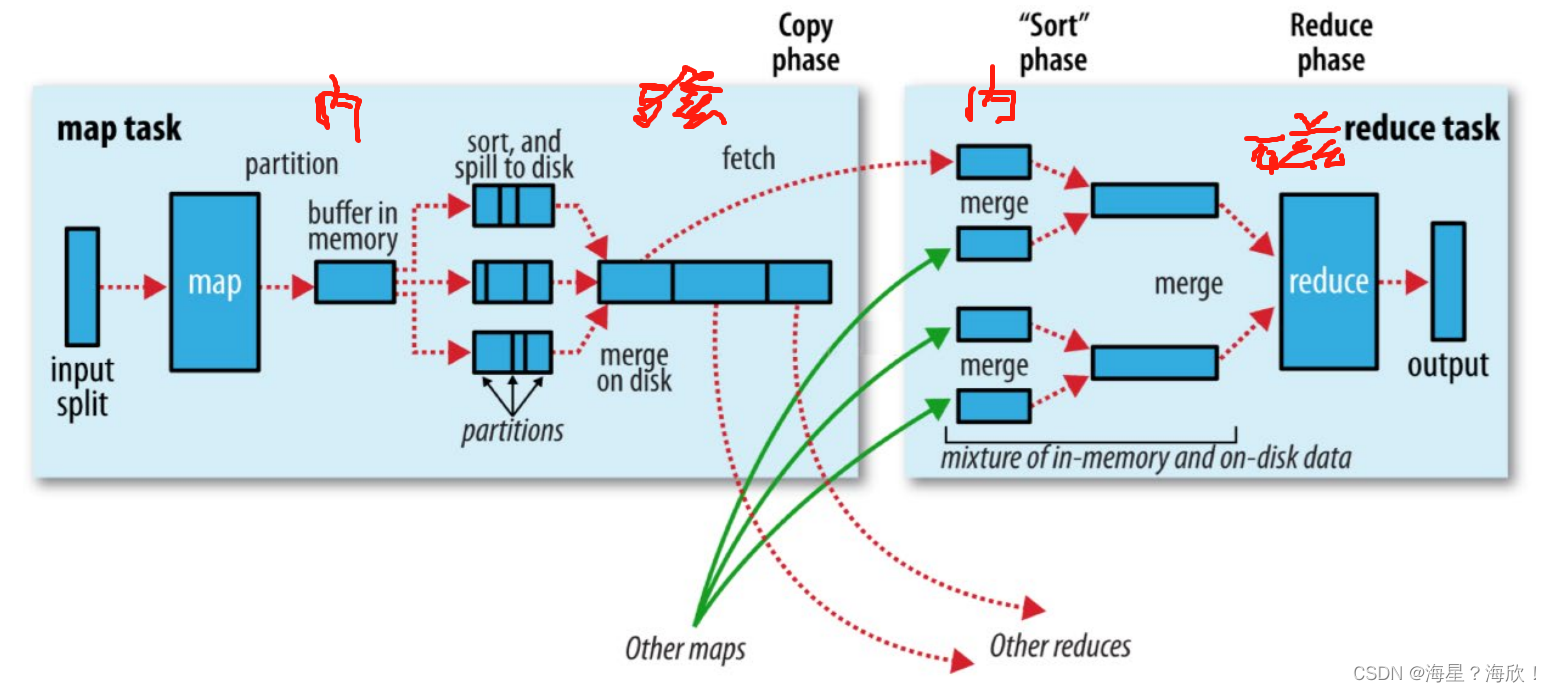
Hadoop MapReduce
目录1.1 MapReduce介绍1.2 MapReduce优缺点MapReduce实例进程阶段组成1.3 Hadoop MapReduce官方示例案例:评估圆周率π(PI)的值案例:wordcount单词词频统计1.4 Map阶段执行流程1.5 Reduce阶段执行流程1.6 Shuffle机制1.1 MapReduc…...
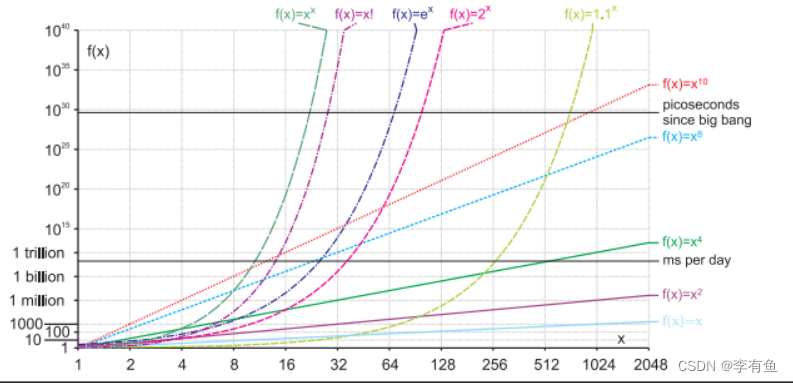
时间复杂度和空间复杂度详解
有一堆数据需要排序,A要使用快速排序,B要使用堆排序,A认为自己的代码更高效,B也认为自己的代码更高效,在这种情况下,怎么来判断谁的代码更好一点呢?这时候就有了时间复杂度和空间复杂度。 目录 …...

【C++】面向对象---封装
【C】面向对象—封装 1.封装的意义 封装是C面向对象三大特性之一 封装的意义: 将属性和行为作为一个整体,表现生活的事物将属性和行为加以权限控制 封装意义一: 在设计类的时候,属性和行为写在一起,表现事物 语…...

Docker简介
一、介绍容器虚拟化技术(带环境安装的一种解决方案)打破程序即应用的观念,透过镜像image将作业系统核心除外,运用应用程序所需要的运行环境,由上而下打包,达到应用程序跨平台间的无缝接轨运作。Docker是基于…...
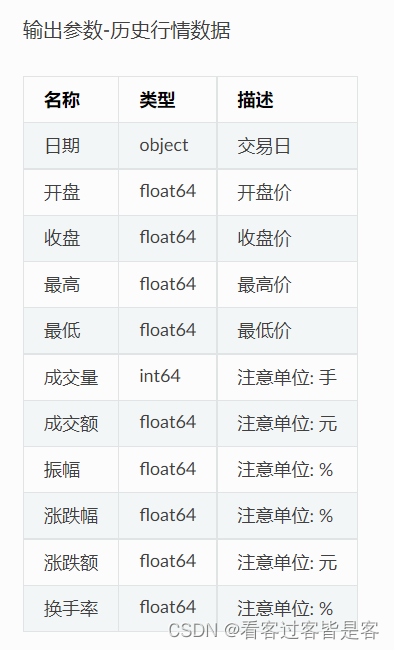
量化学习(一)数据获取
试验环境 windows10 AnacondaPyCharm(小白参考文章:https://coderx.com.cn/?p14) VM中安装MySQL5.7(设置utf8及相应配置优化) 关于复权 小白参考文章:https://zhuanlan.zhihu.com/p/469820288 数据来源 AK…...

java并发编程讨论:锁的选择
java并发编程 线程堆栈大小 单线程的堆栈大小默认为1M,1000个线程内存就占了1G。所以,受制于内存上限,单纯依靠多线程难以支持大量任务并发。 上下文切换开销 ReentrantLock 2个线程交替自增一个共享变量,使用ReentrantLock&…...

大数据框架之Hadoop:MapReduce(三)MapReduce框架原理——ReduceTask工作机制
1、ReduceTask工作机制 ReduceTask工作机制,如下图所示。 (1)Copy阶段:ReduceTask从各个MapTask上远程拷贝一片数据,并针对某一片数据,如果其大小超过一定阈值,则写到磁盘上,否则直…...

Nginx的介绍、安装与常用命令
前言:传统结构上(如下图所示)我们只会部署一台服务器用来跑服务,在并发量小,用户访问少的情况下基本够用但随着用户访问的越来越多,并发量慢慢增多了,这时候一台服务器已经不能满足我们了,需要我们增加服务…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
